関合の卒論日誌

関合の卒論日誌

４年次　卒論研究†

卒論テーマ†

経年により腐朽・劣化が心配される集成材桁橋（深沢橋）の振動特性と健全度評価（タブレットを使った振動試験・現場調査）†

  秋田県大館市に架かっている集成材桁木橋の深沢橋ですが、架設から20年以上経過していることから腐朽劣化が生じている可能性がある。そこで、タブレット端末を用いた振動試験と目視による健全度調査を行う。振動試験からは固有振動数・振動モード・減衰定数・振動使用性などを明らかにし、目視試験からは部材表面の劣化状態について確認を行う。また深沢橋の3Dモデルで振動解析を行い解析値を算出する。もしFAKOPP（応力波伝播時間測定試験機）を借りることができれば、部材のヤング率を測定し、振動試験から推定したヤング率と比較することができれば面白いかも!?

深沢橋　天気†

8月28日†

11月10日†

参考文献†

• 周波数応答関数の実部と虚部の連立を用いたモード特性同定の多自由度系への適用

• SMARTPHONE-BASED VIBRATION ANALYSIS FOR BRIDGE HEALTH MONITORING

• Vibration analysis using mobile devices (smartphones or tablets)

• 加速度センサを用いた道路照明柱の損傷に対するスクリーニング方法の検討

• ボンゴシ材の長期的な腐朽の傾向と診断法の検討

• 端部分離した外ケーブル併用PC吊床版歩道橋の振動使用性

• PC吊床版橋の減衰定数の評価と振動使用性照査における影響

• 橋梁振動実験に基づく斜橋の固有振動数の同定と部材の損傷が振動特性に及ぼす影響に関する基礎的研究

• 遊園地内に架設された人道吊橋の歩行者による水平振動とTLDを用いた制振

• 振動計測の基礎

• 実測データに基づくPC斜張橋の減衰特性について

• 桁橋の鉛直たわみ基本固有振動数を推定するための実用算定式

• 実験と解析に基づく下路式アーチ木車道橋の構造特性評価

• 橋梁振動の人間工学的評価

• 縦桁を有する木製中路式アーチ車道橋の構造特性

• 鶴見つばさ橋の振動実験による動的特性の同定

• 設計時における歩道橋の振動使用性照査法

• 振動感覚を考慮した歩道橋の使用性照査法に関する考察

• 桁形式歩道橋の設計時振動使用性照査手法の提案

• 加速度センサー搭載タブレットを用いためおと橋の振動特性評価

• 橋梁振動の人間工学的評価法

• 設計時における歩道橋の振動使用性照査法

• 木橋の耐用年数

6月7日 matlab†

matlabをダウンロードした。

[操作方法]

①変数の新規変数をクリック

②随時k2からエクセルデータを引っ張ってきて各タブレットに対応するようにデータを入れる（砂袋1回目の1の場所とか）

③FFT1-FFT6まで②で作ったデータを入れる　波形のスタートは480で練習した（同じ試験では同じ波形のスタートを設定）

④band1-band6まで②で作ったデータを入れる　下限上限は卓越した周波数の前後で修正（同じ試験では同じ下限上限を設定）

⑤xcross1-xcross6

⑥Phase14とかPhase16とかで同位相、逆位相の確認（同位相→0°-75°　逆位相105°-180°　位相なし→90°±15°）

⑦各試験（落下位置を変えたものを含む）ごとに保存

[開き方]

cd ~/sekiai/matlabzen → cd bin → ./matlab

メモ：matlabに慣れる。salomeで模型づくり。7月に深沢橋(大館)でフィールドワークの予定。

6月14日†

減衰定数を求める。

[操作方法(gensui)]

①変数の新規変数をクリック

②随時k2からエクセルデータを引っ張ってきて各タブレットに対応するようにデータを入れる（砂袋1回目の1の場所とか）

③gensuiで各数値を入力する

④ワークスペースで保存

[操作方法(hahupower)]

①変数の新規変数をクリック

②随時k2からエクセルデータを引っ張ってきて各タブレットに対応するようにデータを入れる（砂袋1回目の1の場所とか）

③FFT1-FFT6まで②で作ったデータを入れる　

④band1-band6まで②で作ったデータを入れる　

⑤hahupowerで各数値を入力する

⑥ワークスペースで保存

メモ：来週までに減衰定数を求める。

8月21日(月),25日(金),28日(月),(予備日9月1日(金))に大館、三種、森吉の橋で調査を行う。 内容はFAKKOPという応力波伝播速度試験器を用いて部材のヤング率を測定する。

6月28日†

減衰定数を求めたが間違いがあったのでやり直し。

メモ：減衰定数を求め直す。卒論までの見通しを立てる。

7月5日 めおと橋(計算練習)†

波形スタート480

im111 砂袋落下衝撃試験1/4 1回目

im111 砂袋落下衝撃試験1/4 2回目

im111 砂袋落下衝撃試験1/4 3回目

im122 砂袋落下衝撃試験1/2 1回目

im123 砂袋落下衝撃試験1/2 2回目

im124 砂袋落下衝撃試験1/2 3回目

im131 砂袋落下衝撃試験3/4 1回目

im132 砂袋落下衝撃試験3/4 2回目

im133 砂袋落下衝撃試験3/4 3回目

im21 人力鉛直加振試験 1回目

im22 人力鉛直加振試験 2回目

im24 人力鉛直加振試験 3回目

im31 人力水平加振試験 1回目

im32 人力水平加振試験 2回目

im33 人力水平加振試験 3回目

7月12日†

スライド作成をしていた。 外国文献購読の授業で英語で中間発表を行った。 今後のために英語力を身につけたい...

salome-mecaで深沢橋の振動解析を行えたので確認をする。

7月19日†

進展なし。

秋田県では記録的な大雨が続いている。

秋田市を流れる太平川では氾濫が発生し、警戒レベル5に相当する氾濫発生情報が出るなど秋田県内では複数の中小河川が氾濫した。

15日、秋田市仁別で降り始めから24時間雨量が午後6時過ぎに294mmと観測史上最大になるなどの記録的豪雨となっている。

7月26日†

仮想材を作成し終えた。これからメッシュをきって解析をしていく。

夏季休暇†

8月28日(月)　深沢橋でフィールドワークを行ったが、スズメバチの巣があり思うように試験を行えなかった。得られた数値でできることをやっていく。

歩道橋の固有振動数†

fv = 4.96 - 0.067 × L (基準設定以前に建設)

fv = 4.96 - 0.067 × L (基準設定以後に建設)

fv(鉛直方向基本固有振動数),L(支間長m)

参考資料：橋梁振動の計測と解析　橋梁振動研究会編

深沢橋　salome-meca(7.0GPa)†

高欄の仮想材を設定するとファイルが壊れてしまうため、高欄の重さを床版に加えて密度を求めた。

高欄　W=150mm,H=1770mm,L=150mm,N=44個,比重0.38　→　665.874kg

床版　W=3500mm,H=70mm,L=30020mm,比重0.38　→　2794.862kg

　　　W=3500mm,H=70mm,L=30020mm　→　7.3549mm^3

密度　(665.874+2794.862) ÷ 7.3549 = 470.534746 kg/m^3 ≒ 4.7e-10 t/mm^3

E_N→軸方向ヤング率(7000MPa),　E_L・E_T→軸直角方向ヤング率(7000☓(1/25)=280MPa),　G_LT→せん断弾性係数(7000☓(1/15)=467MPa),　NU→ポアソン比,　RHO→密度

modes___DEPL[0] 3.579Hz（鉛直対称一次モード）

modes___DEPL[1] 5.341HZ（水平一次モード）

modes___DEPL[3] 12.429HZ（鉛直逆対称一次モード）

FAKOPP試験†

E ＝ ｖ＾2×ρ×10＾-3　の式を用いてヤング率Eを求める。

ｖ：ｋｍ/ｓ　　ρ(密度)：ｋｇ/ｍ³

ρ ＝ 3.8e-10(t/mm^3) ＝ 0.38(g/cm^3)

ρ ＝ 0.38×10^-3(kg) / 1.0×10^-6(m^3) ＝ 380 kg/m^3

v ＝ 1.0×10^-3(km) / t×10^-6(s)

＊床版は3480×10^-6(km)

ｔ：伝播時間

10月4日†

キャンバーを考慮して歩行荷重の設定をしていく。 鉢の巣の撤去が完了したらしい！？

10月11日†

歩行荷重の設定を引き続き行う。 FAKOPPから求めたヤング率を入れてsalome-mecaで解析していく。

10月25日†

歩行荷重を面で設定するとメッシュが切れない。キャンバーが原因？ そのため、点で歩行荷重を設定していく。

10月20日(金)雨天のためフィールドワークが延期。 11月7日(火)に実施予定。11月10日(金)予備日。

11月1日†

FAKOPPで測定した伝播時間からヤング率を算出した。 その値をsalome-mecaに入力して解析をした。

振動数(Hz)の比較

11月8日†

進展なし。

11月7日に予定していた深沢橋のフィールドワークは10日に延期。

11月15日†

11月10日(金)深沢橋の調査を行ったが雨天のため中断。

得られたデータをまとめていく。

今週末は東北予選。がんばる。

11月22日†

12月22日(金)の10時から中間発表。

部活動を引退したので研究を頑張る。

11月29日†

測定値の時間による補正を終えた。MATLABで解析していく。

床版をシンプルにし、歩行荷重の設定の仕方を変えたら面で与えられたのでそれで進めていく。

集成材の日本農林規格表28 同一等級構成集成材のラミナの等級区分機による等級区分のE 95-F315を用いて解析を行う。

製材の日本農林規格

深沢橋　salome-meca(9.5GPa)†

日本農林規格に則り、みなし架設時の解析をした。

鉛直対称一次モード（3.17Hz）

水平一次モード（6.52Hz）

鉛直逆対称一次モード（14.08Hz）

鉛直対称二次モード（26.20Hz）

12月6日　深沢橋　MATLAB†

タブレットから得られたデータは[time,X,Y,Z,...]の順で並んでいるためD列の値を使用する。

データを０セットする。

６つで比較すると。

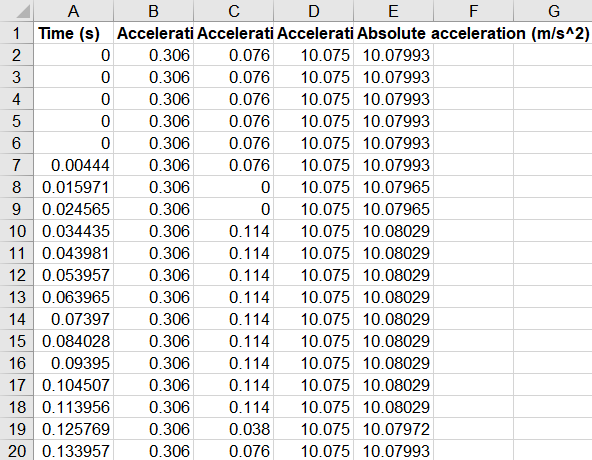
タブレット間による時間補正を行うためにスタートした時間を使用する。

0セットしたデータを使用して補正する。

K2=MATCH(MAX(K6:K1008),K6:K1008,0)

K3==MATCH(MIN(K6:K1008),K6:K1008,0)

K4=MAX(K6:K1008)

K5=MIN(K6:K1008)

L1=L3-\( K \) 3

スタート時間を用いて補正値を算出する。

I5=ROUND(\( H \)4-H5,-1)

K列に上記で算出したデータを入力する。

L5=J5-K5

上記のL列の分補正する。 「-」のときは、その分「0」を足す。 「+」のときは、その分データを減らす。

新規変数より、 補正されたデータをタブレットごとに登録する。

FFT処理。

band処理。

xcross処理。

歩行試験。

振動数に卓越周波数。 加速度に「h1hakai」「h2hakai」を代入。

12月13日†

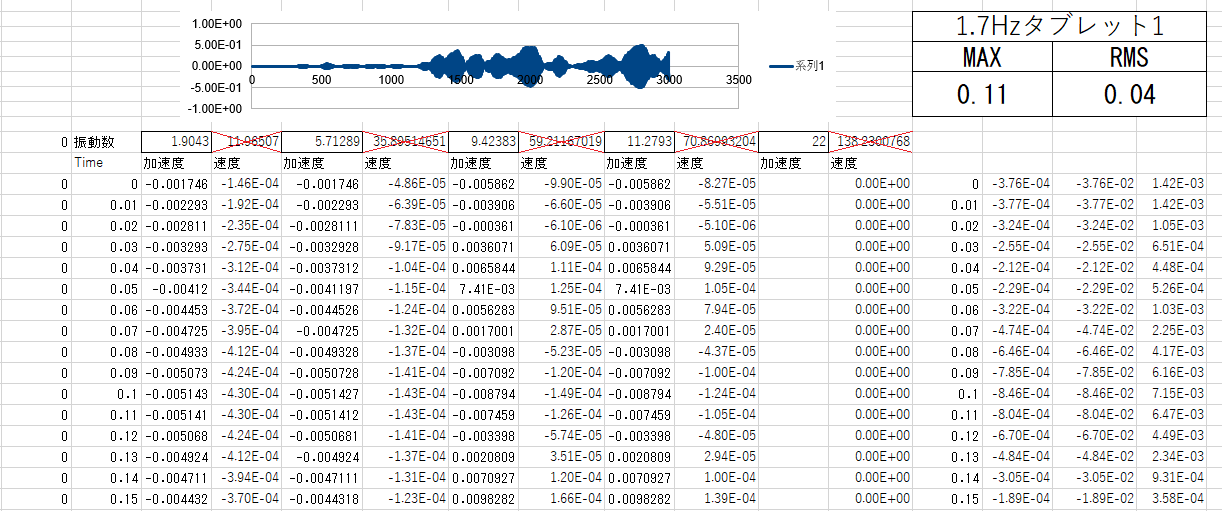
歩行試験の解析から一週間たったが解析が終わらない... どうしようのないので、中間発表に向けて概要とスライドづくりをしていく。

12月20日†

ようやく歩行試験の解析が終わった...と見せかけて実は終わってなかったので今日も先輩のパソコンをお借りしている。 22日の中間発表に向けてTexとスライドづくりを完成させる。

振動使用性†

salome-meca→Split Horizontal→Create View(SpreadSheet View)→Plot Sekection Over Time

上記の解析を各点で行うと このように なるのでExport SpredSheetしてcsvファイルにする。

csvファイルを開き、応答速度の実効値を求める。

ｙ方向速度：max(resharmVITE (1)),cmに変換:=AO3011*0.1,二乗:=AP3011^2,応答速度の実効値:=SQRT(AVERAGE(AQ3011:AQ6011))

次に実測値と比較する。

salome解析加速度:max(resharmACCE (1)),mmをcmに:=C6*0.1,測定加速度:0セットした生データ,mをcmに:=E6*100

1月10日†

設定を変更して解析を行なった。

振動数(Hz)の比較

1月17日†

データが揃ったので振動使用性についての検討を行なった。 評価表はこれやこれを参考にした。

単独歩行

群衆歩行

縦軸：応答速度(cm/s),横軸：歩調(Hz)

※実効値とは測定した加速度を積分して応答速度を出し、その応答速度の最大値を二条平均平方根化したもの。この値で歩行試験の評価を行う。

1月24日†

みなし新設時の固有振動数を8月に測定した振動数(3.125Hz)に合わせることで、橋梁全体の剛性が何％低減しているかを推測。

→結果29.5％ほど低減していると推測した。

1月31日†

一昨日、内定者説明会があった。必要書類が多くて驚き。 とりあえずアパートが決まって一安心。

2月7日†

発表練習で指摘いただいた箇所の修正中。 解析も追加で行わなければいけない。。。

2月14日†

発表まであと一週間となった。がんばろー。

2月19日†

卒業論文発表会が終わった。お疲れ様でした～。

３年次　創造工房実習†

11月11日　片持ち梁　†

片持梁の理論値 6.67mm

11月18日　単純梁†

単純梁理論値 0.4167mm

11月25日　単純梁　異方性：1次要素　等方性：2次要素†

異方性1次 理論値　0.4917mm(ティモシェンコ梁)

等方性2次 理論値　0.4167mm

12月2日 　2部材の単純梁 [#bb9e1071]†

サンドウィッチ梁の理論値　0.099mm

比較？

操作方法†

UNIXコマンド†

• UNIXコマンド
• コマンド集
• 操作系コマンド
• ジャンルごとに細かいもの

gnuplot†

• gnuplot
• gnuplotスクリプトの解説
• 色・形

inkscape†

• inkscapeでDesign
• 凡例のみを消してグラフを残したいときは、「ノードツールで選択→画面上のパス→分解」　をやることで消すことができる。（選択したあとctr+shift+Kでショートカットできる）
• 上記の方法だと色もなくなってしまうので色は、「ノードツールで選択→ストロークの塗り」　で色付け作業をする。

salome†

• 基本的な使い方
• 入門編
• Geometry
• 単純梁
• 振動解析
• 結合

LaTex†

• LaTex入門コマンド
• LaTexコマンド一覧
• 単位の累乗（cm^2,mm^2）をするときは直接cm^2やmm^2で書くのではなく式として認識させるために$で囲う必要がある。
• 図の中に文字の大きさの変え方
• pngの貼り方 \includegraphics[width=30mm]{.png}　（数字は画像の幅の拡大・縮小）
• pdfの貼り方　\input{.pdf_tex}
• \if0 \fi　でコメントアウトしたい行を囲むと複数行のコメントアウトができる。
• esc+uで１つ戻る。

後藤資料†

• 構造研ゼミ [#e122df06]

• 振動測定メモ

• OB,OGの卒論・修論日誌

• 良いプレゼンと悪いプレゼン

最新の100件