![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
CLT床版用の防護柵の開発(安部さんサポート)旭川の実験モデルをSalome-Mecaで再現(小川さんの修論や安部さんの卒論のモデル化)。
2つに割れている鞘管が1つずつ順番に降伏することで、どれぐらいエネルギーを吸収できているかを評価。
https://www.str.ce.akita-u.ac.jp/~gotouhan/j2023/hattori23/防護柵支柱試験_2024.odg
↑防護柵 図面
・小川さんの論文 CLT床版への取付・交換を考慮した鋼製防護柵の破壊挙動, 構造工学論文集,Vol. 70A, p. 885-893, 2024/3. https://doi.org/10.11532/structcivil.70A.885
・小川さん 卒論:CLT床版に取り付けられた鋼製防護柵の性能評価 (概要 https://www.str.ce.akita-u.ac.jp/kouzou/pdf/so20og.pdf、スライド https://www.str.ce.akita-u.ac.jp/kouzou/pdf/so20ogp.pdf)
・小川さん 修論:CLT 床版への取付・交換が容易な鋼製防護柵の破壊挙動(スライド https://www.str.ce.akita-u.ac.jp/kouzou/pas/sy22ogp.pdf)
・安部さん:支柱交換を考慮したCLT床版用鋼製防護柵の挙動(概要 https://www.str.ce.akita-u.ac.jp/kouzou/pas/so22ab.pdf、スライド https://www.str.ce.akita-u.ac.jp/kouzou/pas/so22abp.pdf)
! <BoucleGeometrieError> <MECANONLINE9_9> ! ! ! ! Arrêt par échec dans la boucle de point fixe sur la géométrie. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. ! <ループ・ジオメトリー・エラー> <MECANONLINE9_9> ! ! ! ! ジオメトリの固定点ループの失敗で停止 ! ! グローバルデータベースが保存される。停止前のステップが保存されています。
角柱のモデルを正12角形から正24角形に変更して解析を回してみている。その後まず支柱を自重程度で固定したモデルを回してみる
前回の正12角柱と比較したものが
スリットサイズが正12角柱が30mmで正24角柱が24mmになっている。
この正24角柱のモデルに支柱をかぶせて拘束荷重を与えたモデルが
ただこれはエラーが出てしまった。
! <MatriceSinguliereError> <MECANONLINE9_4> ! ! ! ! Arrêt pour cause de matrice non inversible. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. ! ! ! ! Conseils : ! ! - Vérifiez vos conditions aux limites. ! ! - Vérifiez votre modèle, la cohérence des unités. ! ! - Si vous faites du contact, il ne faut pas que la structure ne "tienne" que par le contact. ! ! ! ! - Parfois, en parallèle, le critère de détection de singularité de MUMPS est trop pessimiste ! Il reste néanmoins souvent ! ! possible de faire passer le calcul complet en relaxant ce critère (augmenter de 1 ou 2 la valeur du mot-clé NPREC) ou ! ! en le débranchant (valeur du mot-clé NPREC=-1) ou en relançant le calcul sur moins de processeurs. !
MatrixSinguliereError> <MECANONLINE9_4> !
! ! ! 非可逆行列のため停止 ! ! グローバルデータベースが保存される。停止前のステップが保存されている! ! ! ! アドバイス: ! ! - 境界条件をチェックしてください! ! - モデルと単位の整合性をチェックする! ! - 接触を使用する場合、接触だけで構造を保持してはいけません! - 並行して、MUMPSの特異点検出基準が悲観的すぎることがある!しかし、多くの場合、まだ可能である! この基準を緩和する(NPRECキーワードの値を1または2増加させる)か、! 切断する(NPRECキーワードの値を1)か、より少ないプロセッサで計算を再実行することによって!
接触のみで支柱を固定しようとしたことが原因と思われる。
圧縮側の接触部分に半円の仮想材料を挟んでみる。
以前の中間発表で用いたモデルが鞘管と下の鋼板がしっかりとくっついていなかったせいか、下図のような結果が出てしまっていた為、円柱から多角柱のモデルを作成して確実に隙間のないモデルを作成してみることになっていた。
そこでまず次のような正12多角柱の鞘管モデルを作成して解析した結果次のようになった。
続いてこのモデルに穴を開けずに鞘管を鋼板に一体化させたモデルを解析した結果このようになった。
この結果がうまく行っていた為、次のような穴を開けたモデルを解析した結果次のようになった
この結果からメッシュの隙間はないほうがいいと言えると思った為、円柱のときにメッシュの隙間ができないようにモデルを一体化させた後に穴を開けたモデルを作成した結果次のようになった。
一旦中間発表時点で出ていた一つの問題はジオメトリでの作成方法でなんとかなるようだった。
円柱の結果と角柱の結果を比較してみたら
青が角柱 オレンジが円柱
圧縮側の鞘管の降伏のタイミングが違うのは円柱と角柱のスリットサイズが違うため。
スリットサイズを揃えた鞘管のみの角柱のモデルでエラーが出てしまっていて、本当にモデルの形状のせいなのかわからないがスリットのサイズを変更してモデルの形状を変更したら解析が回ったためこのようになっている。
この時出て解決できなかったエラー
! <EXCEPTION> <ADAPTATION_11> ! ! ! ! La valeur du pas de temps retenu < 8.910094884129e-13> est inférieure à PAS_MINI. !
PAS_MINIで設定できる最小値は1e-12までなのでどうすれはいいかわからず解決できなかった。
円柱のモデルで降伏のタイミングが早くなってしまっているように見える原因はまだよくわかっていない
縦軸を縦軸モーメント、横軸を変位として値をそろえて比較した結果上記のようになった。青が今回行ってきた解析結果でオレンジが過去の実験の結果。
変位を揃えるために、解析結果の方の変位を支柱と鞘管の高さの比率と同じ分大きくして3.51倍にしている。
このようなズレが生じた原因としてはまず、私の行った解析結果は鞘管のみでかつ、鞘管の変位を見ているため、当然実験結果の支柱の変位より値が大きくなってしまっている。
次に実験では鞘管に支柱を固定するためのボルトが刺さっている為、その分降伏が遅くなることも予想できる。
そのため実験に近い形のモデルを作成する必要がやはりあると言える。
まず、接触面を平行に直す前の実際の実験と同じモデルで同じ設定を使い解析を回してみたがやはり回らなかった。
<S> Exception utilisateur levee mais pas interceptee. ! ! Les bases sont fermees. ! ! Type de l'exception : NonConvergenceError ! ! ! ! Arrêt pour cause d'absence de convergence avec le nombre d'itérations requis ! ! dans l'algorithme non-linéaire de Newton. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant ! ! l'arrêt. ! ! ! ! Conseils : ! ! - Augmentez ITER_GLOB_MAXI. ! ! - Réactualisez plus souvent la matrice tangente. ! ! - Raffinez votre discrétisation temporelle. ! ! - Essayez d'activer la gestion des événements (découpe du pas de temps par ! ! exemple) dans la commande DEFI_LIST_INST.
ピンクの点がデータを取った箇所
荷重863N/mm (200mm[h]×862.8 N/mm ×130mm[線荷重]=22432800 Nmm
(過去の実験値 701mm[h]×320 N/mm ×100mm[線荷重]=22432000 Nmm
縦軸モーメントを基準に比較をしようとしたが、よくよく考えたらモーメントを揃えても実験結果のグラフしか持っていなかったので、実験と同じモデルを用意して解析をやってみる。
<EXCEPTION> <FACTOR_11> ! ! ! ! Problème : la matrice est singulière ou presque singulière : ! ! Lors de la factorisation de la matrice, on a rencontré un problème ! ! (pivot nul ou presque nul) à la ligne 406 qui correspond au degré de liberté donné ci-dessus. ! 問題:行列が特異またはほとんど特異である: ! ! 行列を因数分解すると、問題が発生した! ! (ピボットがゼロまたはほとんどゼロ)が406行目にあり、これは上で与えられた自由度に対応する。 ! ! ! Risques et conseils : ! ! * Si la ligne correspond a un degré de liberté physique, il s'agit probablement d'un mouvement ! ! de corps rigide mal bloqué. ! ! Vérifiez les conditions aux limites. ! ! Si vous faites du contact, il ne faut pas que la structure ne "tienne" que par le contact. ! ! Vérifiez également les caractéristiques matériaux (module d'Young, ...). ! リスクとアドバイス: ! ! * その線が物理的自由度に対応している場合、それはおそらく! の動きである可能性が高い! ! 境界条件をチェックする! ! 接触している場合、その構造は接触によってのみ「保持」されてはならない! ! また、材料の特性(ヤング率など)もチェックしてください。 ! ! ! * Si la ligne correspond a un degré de liberté de Lagrange, il s'agit sans doute d'une condition ! ! limite redondante. ! ! En particulier, il se peut que la relation linéaire surabondante provienne des conditions de contact. ! ! Peut-être devriez vous exclure certains noeuds des conditions de contact ! ! (mots clés SANS_NOEUD et SANS_GROUP_NO). ! 線がラグランジュの自由度に対応する場合、これはおそらく条件である! 冗長限界! ! 特に、その冗長な線形関係は、接触条件から来ているのかもしれない! ! 接触条件からいくつかの節点を除外すべきかもしれません! ! (キーワードWITHOUT_NOEUDとWITHOUT_GROUP_NO)。 ! ! ! * Si le solveur utilisé est LDLT ou MULT_FRONT, vous pouvez utiliser le solveur MUMPS ! ! car celui-ci est le seul à pouvoir factoriser les matrices qui ne sont pas définies positives. ! 使用するソルバーが LDLT または MULT_FRONT の場合は、MUMPS ソルバーを使用できます! これは正定値でない行列を因数分解できる唯一のソルバーである。 ! ! ! * Parfois, en parallèle, le critère de détection de singularité de MUMPS est trop pessimiste ! Il reste néanmoins souvent ! ! possible de faire passer le calcul complet en relaxant ce critère (augmenter de 1 ou 2 la valeur du mot-clé NPREC) ou ! ! en le débranchant (valeur du mot-clé NPREC=-1) ou en relançant le calcul sur moins de processeurs. ! 並行して、MUMPSの特異点検出基準が悲観的すぎることがある!しかし、多くの場合、まだ可能である! この基準を緩和する(NPRECキーワードの値を1または2大きくする)か、! 切断(NPRECキーワードの値を1)するか、より少ないプロセッサで計算を再開する。 ! ! ! * Il se peut aussi que ce phénomène soit tout à fait normal avec X-FEM si la fissure passe ! ! très près d'un noeud. ! ! Si le nombre de décimales perdues n'est pas trop grand (max 10 décimales), ! ! vous pouvez relancer le calcul en augmentant le nombre de décimales perdues autorisé : ! ! mot-clé NPREC du mot clé facteur SOLVEUR. ! ! Sinon, contactez l'équipe de développement. また、亀裂が節に非常に近いところを通過する場合、X-FEMではこの現象が完全に正常である可能性もある! 節に非常に近い! ! 失われた小数点以下の桁数がそれほど大きくなければ(最大小数点以下10桁)、! 小数点以下の桁数を増やして計算を再開することができます! キーワード係数SOLVEURのキーワードNPREC! ! そうでなければ、開発チームに連絡してください。
2種類の鋼材を合わせた隙間のないモデル(岐阜高専さんの使っていたもの)で摩擦なしの設定やdiscreatで摩擦を考慮したものが回ることを確認した上で、continueを使いかつ摩擦係数を加える設定(ラグランジュ法)を使って解析を回そうとすると上記のようなエラーが出てしまう。
まず、岐阜高専さんのやり方でやっていた時、接触面に共通のノードがある、というエラーが出ていた為、片方の部材のメッシュサイズを変更した上でそれでもかぶるノードをジオメトリでグループ化してsans_grop_noに追加してあげることでエラーを解決していたが、continue変えて摩擦係数を設定したりすると上記通りsans_grop_noに関係するエラーが出てしまっていた為、これを消すために片方の部材を0.1mmだけ横にずらしてあげることで共通ノードがないようにして解決させたが、当然上記エラーの原因はこれだけではなかった。
一旦今後の方針として後藤先生と相談した結果、摩擦なしの設定を使って一応結果が得られているため、実際の実験結果や小川さんの使っていたものと結果の比較をしたりしていくことになった。比較は高さ×荷重で縦軸モーメントを用いて比較を行う。また、スリット部分を今は平行にしてやってきたけれど、それをもとに戻して解析が回るかも確認してみる。摩擦有りものもに関しては今後隙間を見ていろいろ試していく。
<NonConvergenceError> <MECANONLINE9_7> ! ! ! ! Arrêt pour cause d'absence de convergence avec le nombre d'itérations requis dans l'algorithme non-linéaire de Newton. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. ! ! ! ! Conseils : ! ! - Augmentez ITER_GLOB_MAXI. ! ! - Réactualisez plus souvent la matrice tangente. ! ! - Raffinez votre discrétisation temporelle. ! ! - Essayez d'activer la gestion des événements (découpe du pas de temps par exemple) dans la commande DEFI_LIST_INST. <NonConvergenceError> <MECANONLINE9_7> ! ! ! ! ニュートンの非線形アルゴリズムにおいて、必要な反復回数で収束しなかったため停止しました! ! グローバルデータベースが保存される。停止前のステップが保存されている! ! ! ! アドバイス: ! ! - ITER_GLOB_MAXI を増やす! ! - タンジェント行列の更新頻度を上げる! ! - 時間離散化を洗練させる ! ! - DEFI_LIST_INSTコマンドでイベント管理(例えば時間ステップの切断)を有効にしてみてください。
conotinueを使って摩擦を考慮した解析を回していっているが、摩擦係数を入れたり、ペナルティ法を使ってみると上記のエラーが出てしまう。荷重を1N/mmずつ変えていってみたところ、接触が起きたタイミングでこのエラーが出てしまっている。
前回の鞘管のモデルをdiscreatを使って解析を回していたがうまくいかった。
これまでに摩擦を考慮した簡単なモデルをやったことがなかったということで一度鋼材板2枚のモデルで解析をやってみることにした。
ただうまくいかず、安部さんによると現在の設定だけでは足りずいろいろ増やす必要があるらしかった。そもそもdiscreatとcontinueの違いが ×(強制荷重を加えて変形を示す)→「荷重拘束を使用する」か、はたまた ×(普通に荷重を加える)→「変位拘束を使用する」かの違いらしく、discreatを使って荷重を使おうとすると今回のようにエラー(下のやつ)が出たりうまくいかない上に更にいろいろ設定を増やす必要がある。その上、解析結果の違いはないらしいので今後は一旦continueを使って進めていくことにする。この設定でも摩擦の設定ができるらしいので試していく。
Erreur> Échec dans le traitement du contact discret
<Action> On essaie de découper le pas de temps.
On utilise la découpe manuelle.
Découpe uniforme à partir de l'instant < 6.000000000000e-01> en <4> pas de temps.
(soit un incrément constant de < 1.942890293094e-16>)
Le pas de temps minimum < 1.000000000000e-20> (SUBD_PAS_MINI) est atteint.
<Action><Échec> Échec dans la tentative de découper le pas de temps.
!<TraitementContactError> <MECANONLINE9_5> !
! ! ! Arrêt pour cause d'échec lors du traitement du contact discret. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. !
摩擦を考慮するためにdiscreteを使った設定を作成中
! <A> <JEVEUX1_64> ! ! ! ! Le volume des données temporaires (objets de la base Volatile) écrites sur disque (110.16 Mo) ! ! est plus de 100.00 fois supérieur au volume de données lues (0.78 Mo). ! ! ! ! Risques et conseils : ! ! Ce déséquilibre n'a pas de conséquence sur les résultats de calcul, il indique simplement que ! ! certaines structures de données temporaires ont été écrites sur disque et détruites sans avoir ! ! été relues. C'est le cas lorsque vous utilisez le solveur MUMPS, car certaines structures de ! ! données sont volontairement déchargées pour maximiser la mémoire lors de la résolution. ! ! ! ! ! ! Ceci est une alarme. Si vous ne comprenez pas le sens de cette ! ! alarme, vous pouvez obtenir des résultats inattendus ! !
! ディスクに書き込まれた一時データ(揮発性データベース・オブジェクト)の量(110.16MB)が、読み込まれたデータ量(0.78MB)の100.00倍以上である。 !
! ! ! リスクとアドバイス: ! ! この不均衡は計算結果には何の影響もなく、単に特定の一時的なデータ構造がディスクに書き込まれ、再読み込みされることなく破棄されたことを示している。これは、MUMPSソルバーを使用する場合であり、特定のデータ構造は、解答中にメモリを最大化するために意図的にアンロードされるためである! ! ! ! ! ! これはアラームである。この! アラームの意味を理解していないと、予期せぬ結果を招くことがあります!
このエラーと接触不良に関するエラーが消えない。
contenueを使った設定では上記のような結果を得ることができた。 ただこの設定で摩擦を考慮できているのかがよくわからないため、discreteのやつで摩擦を考慮できる設定のものをできるようにしてみる。
中間発表のものはdiscreteでやっていたが摩擦を考慮しない設定になっていたことに気づいた。
このグラフは上のparavisの結果を使って右側の鞘管の載荷線部分中央1点をプロットして荷重−変位を見たグラフで、左のグラフが800N/mmを加えた時で右は600N/mmを加えたときの結果。
これまで使ってきた設定をノート等に調べてまとめている。
接触面が複数ある場合はzoneのアイテム数をその分増やす必要があるらしい。
discreteからcontinueにかえて、それに伴う設定も変えてみて解析をしてみたら
! <MatriceSinguliereError> <MECANONLINE9_4> ! ! ! ! Arrêt pour cause de matrice non inversible. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. ! ! ! ! Conseils : ! ! - Vérifiez vos conditions aux limites. ! ! - Vérifiez votre modèle, la cohérence des unités. ! ! - Si vous faites du contact, il ne faut pas que la structure ne "tienne" que par le contact. ! ! ! ! - Parfois, en parallèle, le critère de détection de singularité de MUMPS est trop pessimiste ! Il reste néanmoins souvent ! ! possible de faire passer le calcul complet en relaxant ce critère (augmenter de 1 ou 2 la valeur du mot-clé NPREC) ou ! ! en le débranchant (valeur du mot-clé NPREC=-1) ou en relançant le calcul sur moins de processeurs. !
!非可逆行列による停止 ! ! グローバルデータベースが保存される。停止前のステップが保存されています! ! ! ! アドバイス: ! ! - 境界条件をチェックしてください! ! - モデルと単位の整合性をチェックする! ! - 接触を使用する場合、接触だけで構造を保持してはいけません! ! ! ! - 並行して、MUMPSの特異点検出基準が悲観的すぎることがあります !それでも、しばしばこの基準を緩和する(NPRECキーワードの値を1または2大きくする)か、あるいは !切断する(NPRECキーワードの値を1にする)か、より少ないプロセッサで計算を再開する。
荷重のかけすぎ、または特定の点に荷重が集中しすぎてしまっている可能性、固定条件が弱い可能性、接触に関する問題がある可能性があるらしい。
一旦鋼材二枚のモデルにこの設定で試してみる
→小さいモデルだと解析で計算してくれず、大きくしたもので試したら同様のエラーが出てしまった。
弾塑性を消して解析を回してみたりもしたが結果は変わらなかった。
岡田さんのcontinueを使用してうまく行ったhdfファイルを借りて岡田さんの作ったモデルが回ることを確認してから自分のモデルを回してみたが、解析は回らず、エラーが出てしまった。
→DEFI_CONTACTのCONTACT_INITをNONに変更したら解析が回った。もともと岡田さんが回していたモデルは2つの物体がくっついているモデルだったのに対して自分の使っていたものは間が合いていることが原因だったようで、DEFI_CONTACTのCONTACT_INITは接触の初期条件の設定だったため、ここを最初くっついているモデルは「OUI」で離れているモデルは「NON」にする必要があるらしい。
warp by vector が何故か使えないため https://note.com/mmer547/n/n1a0ce48712e4 これを参考に試してみる
以前のモデルで接触面の設定を変えたものはうまく行ったが、鞘管のモデルのものはDEFI_CONTACTの設定を増やしたが結果は変わらず。別の要因がある様子。
! <TraitementContactError> <MECANONLINE9_5> ! ! ! ! Arrêt pour cause d'échec lors du traitement du contact discret. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt.
前回のモデルの解析は要素数が47000程度のものだと解析に4日以上かかった上にメモリ不足によるエラーが出てしまったため、要素数を7900程度まで落としたところ、5〜6時間程度で解析が回った。ただ、「 個別コンタクトの処理に失敗し、停止しました!グローバルデータベースが保存される。停止前のステップが保存されている。」といった内容のエラーが出てしまっていた。
このエラーの原因がよくわからなかったため、今まで参考にしてきたモデルは接触する面と接触される面の設定が一箇所ずつだったのに対して今回は複数あることが原因と仮定して、二枚の板のモデルで下図のような接触面を用意して解析を回してみる。
→DEFI_CONTACTの設定より、 触する面と接触される面の設定でitemの数を増やす。
円柱状のモデルを作成。サイズやスリットの角度などはCtype4.hdfに使われていたものを参考に作成した。
解析時間は26時間ほど。加えた荷重は線荷重で引張側の鞘管の上部に設定し、320N/mm加えてみた。
解析結果は「接触不良によるエラー」が出てしまい解析が回らなかった。
詳しい原因はわからないが、おそらく今までは線が面に接触するような解析だったのが、今回はスリット部分に角度がついていて接触する部分が線と線になってしまい、きれいに押せず、不安定だったからではないかと考察する。
そのため一旦次のモデルは実際のものとは少し違うが、スリット部分の断面が平行になっているようなモデルで一度解析を回してみる。
↑のようなモデルを作成してみたため現在解析を回してみている。
大きさを変えても問題がないかの検証のため、200×130×9mmのモデルで解析を回してみた。 線荷重を100N/mm加えた結果、解析自体は回り、時間は26時間程度だった。
今回は少し荷重が足りず、2つめの鋼材が降伏しきるところまでは確認できなっかたけれど、接触したであろうタイミングで荷重と変位のグラフより、上の鋼材が降伏した後に再び線形を示していたため、おそらく大丈夫だと思われる。
今度時間があるタイミングでもう一度荷重を増やして回してみる。
とりあえず次の段階として実際に用いられているモデルと同じ2箇所のスリットの入った鞘管と同じサイズの円柱のモデルを作成して解析を回してみる。
以前までのモデルサイズの1/10での接触解析はparavisや荷重−変位のグラフ、応力歪曲線を見た時、うまくできたかと思われる。
まずジオメトリでの作成の際はモデル本体作成後、グループ作成より接触面を設定。詳細メッシュ用の部分も同様に作成。
メッシュの作成時いつもどうりにメッシュサイズを設定後、サブメッシュの作成より詳細メッシュ部分のメッシュを本体のメッシュサイズよりも小さく設定する。 その後メッシュを切る。今回は全体を1つとしてメッシュを切ってうまく行ってしまったが、今後モデルサイズを大きく変更した際、うまくいかなくなる可能性がある。
aster-studyでは以下を使用した。
| コマンド名 | 使用用途 | カテゴリーの名前 |
| LIRE_MAILLAGE | メッシュの選択 | mesh |
| AFFE_MODELE | モデル形状の指定 | model Definition |
| DEFI_MATERIAU | 材料諸量の指定 | material |
| AFFE_MATERIAU | 各モデルの材料諸量の指定 | material |
| DEFI_FONCTION | 時間の指定 | Functions and Lists |
| DEFI_LIST_INST | 時間ステップ幅の自動調整機能の設定 | Functions and Lists |
| DEFI_LIST_REEL | 時間ステップの指定 | Functions and Lists |
| AFFE_CHAR_MECA | 境界条件の指定 | BC and Load |
| DEFI_CONTACT | 摩擦なしの接触の指定 | BC and Load |
| STAT_NON_LINE | 非線形解析の設定 | Analysis |
| CALC_CHAMP | 計算の指定 | Post processing |
| IMPR_RESU | 出力の指定 | output |
接触解析メモのページにかかれていたものとほとんど使っているものは同じだが、 DEFI_LIST_INSTの時間ステップ幅の自動調整機能の設定をしないとエラーが出てしまったため、ここも設定した。
STAT_NON_LINEでNEWTONの設定でMATRICEがTANGENTEだとエラーが出てしまっていたため、これをELASTIQUEにしたらうまく行った。
解析時間短縮のためSTAT_NON_LINEのCONVERGENCEのRESI_GLOB_MAXIを0.1にした。ここの値が小さいほど解析結果の許容できるラインが高くなるため、精度は良くなるけれど時間がかかるらしい。
DEFI_LIST_INSTのADAPTATION よりEVENEMENTはSEUILで設定。ECHECのSUBD_METHODEはMANUELで設定。
DEFI_CONTACTのFORMULATIONはDISCRETEで設定した。
今回は線荷重で荷重を加えて載荷を行った。
おそらく前回一定に降伏してしまった原因は境界条件の設定をしていた時、荷重を設定するのではなくDDL_IMPOより強制変位を設定することで降伏を再現していたため、それをtimeで分割した分一定間隔で表示しまっていたのかと思われる。そのためこの設定をやめて以前と同じ線荷重を与える設定にしてこのモデルでの鋼材の曲げ応力度を使って曲げモーメントから荷重を計算して与えて見たところ、解析が回ることが確認できたから荷重を増やして解析を回してみたら、4時間経っても半分くらいしか解析が回っていなかったためとても時間がかかっている。
現在接触解析をうまくできないか試していっているが、岐阜高専さんの方法を参考に進めていってみたところ、下の鋼板をすり抜けず上の鋼板が降伏して下の鋼板を押す様子を確認することができた。接触解析を行う際、部材間が空いていた場合、荷重を加えた後接触する箇所を限定的にせず、接触がある面全体を接触面として設定しても問題ないかもしれない(要検証)。
ただ、鋼材としての挙動があきらかにおかしく、一定にずっと降伏してしまった。多分設定を間違えているだけだから探してみる。
バージョンの違いも有り、設定を変えていく必要があったり、接触解析について書かれていた本とかなり方法が違ったりとしたため、もう少しいろいろ試してみたい。
まず200×130×9の鋼板1枚のモデルを荷重5N/mm^2をかけ解析をまわした結果より、降伏点を2.7N/mm^2 と判断。
縦軸 荷重 横軸 鉛直方向変位
応力-ひずみ曲線のグラフと降伏度周辺のデータ (左 ひずみ 中央 主応力 右 荷重)
続いて鋼材2枚で仮想材料を挟んだモデルは鋼材の厚さが9mmで仮想材料が7mmのものを用意した(以前までのものとは別に作り直した)。7mmにした理由は鋼材1枚で解析を回したときに、鋼材が降伏点を経過して十分に鋼材の降伏が確認できる変位分を仮想材料の厚さにすることで、2枚の鋼材を順番に降伏させたときに上の鋼材が下の鋼材に当たる時、上の鋼材が降伏した状態を再現したかったため(あくまで仮想材料は二枚の鋼材が実際に接触する様子を再現するためにいれたのもの)。この仮想材料のヤング率は0.7でポアソン比は0.001。この値にした理由は、ヤング率は小さければ小さいほど柔らかく変形しやすが、これ以上小さくするとParavisでみた時、挙動がおかしくなってしまうため。ポアソン比に関しては、ポアソン比が0に近い場合、仮に縦に荷重を加えても横に膨らんだりしにくくなるため。結果としてスポンジのような仮想材料となっている。荷重は13N/mm^2にしている。
載荷面の6点をプロットして荷重と鉛直方向の変位をグラフに落として確認したが結果は1回分の降伏の様子しか見れなかった。

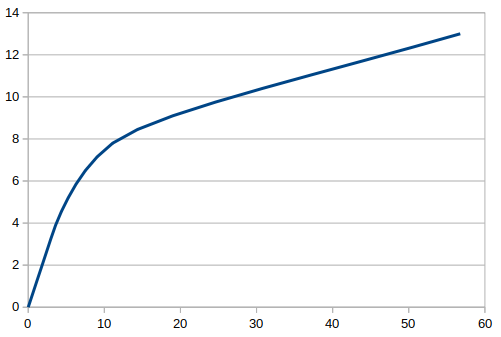
このモデルの応力-ひずみ曲線を圧縮側の中央一点を上の鋼材と下の鋼材をそれぞれ見てみると次のような結果が見られた。
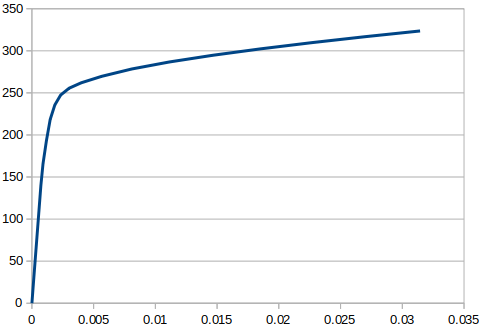
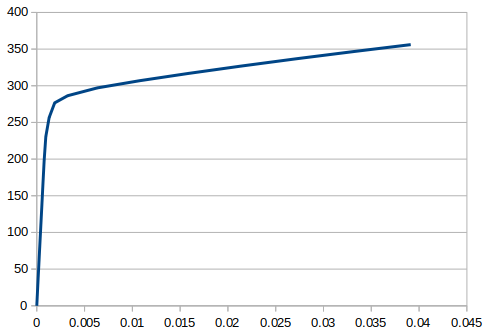
左 上の鋼材の応力-ひずみ曲線 右 下の鋼材の応力-ひずみ曲線
とりあえず2つの鋼材は降伏していることが見受けられる。
ただ、荷重と変位の実際の実験結果を再現できそうではなかったため、次にバネ要素を用いたモデルを作成することになった。
上記図のような載荷面側の片側のみ、計14個の7mmのバネ要素を取り入れ作成した。このバネの剛性を設定する時、xとy軸方向には変位できないように高い剛性を与え、(https://archives.framabook.org/docs/Code_Aster/beginning_with_code_aster-jp_aubry-20190129.pdf)を参考に100000とし、z軸はフックの法則より剛性を決め、ばね定数とした。ただ、この時のばね定数の値をどうするべきかわからなかったため、とりあえずバネの変位が7mmまで変形できるとしたもの(物理的にはありえないが)と、変位が5mmとしたものを想定して、使用した荷重は解析によって得られた一枚の鋼材の降伏点である2.7N/mm^2として、ばね定数をそれぞれ32N/mmと45N/mmとした。そしてばね定数の大きいものとして80N/mmのものでも解析をまわすことにしてみた。 バネ定数を32N/mmのモデルに荷重を10N/mm^2かけてみた結果次のようになった。
上の鋼材に変位は見られたものの、下の鋼材変位がほとんど見れる前に荷重をこれ以上加えられなくなってしまった。
ばね定数を80N/mmにして荷重を8N/mm^2かけてみた結果
ばね定数を56N/mmにして荷重を8N/mm^2かけてみた結果
応力歪曲線も確認してみたかったが、EPEQがバネ要素を用いていると設定できないためしっかりと確認することができない。
ここまで接触解析を用いずに接触を容易にモデル化するために仮想材料やバネを用いてきたが、求めている結果が得られなかったため、夏休みの期間を用いて接触解析を行ってみる。
そのために接触解析のための簡単なモデルから試してみる。
全体にバネを設定していたのを載荷面側の一列のみに変更。
今まで降伏点を理論値のもので考えてしまっていたため、もう一度1枚のみの鋼材で降伏点を確認して、そこから少しグラフで降伏している様子が見られるぐらいの変位のぶんをバネの長さにしたため、バネの長さが3.3801から7mmに変更。
→(こうすることで仮想材料を入れていたときのものに変化がないか複数回解析を回してみたが変化はなかった。)
変位に対する剛性(ばね定数?)を32N/mmにし、荷重を10Nに設定して解析を回した。
バネの変位に対する剛性を30にしたが下の鋼材に接する程の荷重を与えようとするとエラーが出てしまう。(15が限界)
バネの変位に対する剛性を15にすると鋼材は貫通してしまった。
バネの変位に対する剛性を18で荷重を15加えると
下の鋼材が少しだけ圧縮されているもののあまり変位が見られない。
10×10間隔でバネ要素を断面全体に取り込んだモデルの解析を行った結果、解析は回った。ただまだ鋼材がすり抜けてしまったため、バネの剛性を大きくしてみる。現在x軸方向の変位に対する剛性が100,000、y軸が100,000、z軸が1だったため(z軸方向の変位を見たく、徐々に剛性を高めていくつもりだったため)ここの値を大きくしてみる。現在の荷重は面載荷で6。
バネ要素のz軸の剛性を10以上にしないと鋼材が貫通してしまい、50だと仮想材料の時と同じく2枚同時に降伏してしまった。そのため、20にして試したが、かけられる荷重が15が限界で、それ以上はエラーが出てしまった。しかし今まで1番良さそうな挙動を示した。ただ、荷重と変位のグラフを作成すると降伏がしっかりみられないグラフになってしまった。
↑荷重15 バネのz軸方向の変位に対する剛性20N/mm
前回2枚の鋼材の間に仮想材料の代わりにバネ要素を使ったモデルの試し用のバネ一つだけを入れたモデルを作成して解析を回してその日は終わったが、とりあえず解析は回った。DIS_Tを使う場合はEPEQを使用しているとエラーが出てしまっていたため、消しておく必要があった。 予想はしていたが、バネ一つだけでは上の鋼材が降伏したあとそのまま下の鋼材をすり抜けてしまったため、今度は全体にバネ要素を入れたモデルを作成して解析を回した。
この解析を回す時バネ要素が鋼材と接している部分がメッシュを切った時の接点でないと色々なエラーが出てしまったため鋼材に格子状の線を入れることが必要だった。
今まで荷重が10までしか回っていなかったが仮想材料がヤング率0.7、ポアソン比0.1のときにとりあえず荷重を13で回してみたら、解析が回った。しかしグラフは一段階の降伏しかみられなかった。
どうしても部材が同時に降伏してしまっているようで今まで以上の荷重をかけてもそこからの変位は一定に変化してしまっている。そのためこれ以上荷重を大きくしても意味がないと思われる。
仮想材料のヤング率を0.01から0.1にしてみたが同様にすり抜けてしまった。
ヤング率を0.5、0.7にし、載荷を10にして解析を回したが、すり抜けこそなかったが、グラフは以前と同様、1段階分の降伏しか見られなかった。
直方体の仮想材料を入れるだけではうまくいかなかったので次はバネ要素を取り入れてみることになった。鋼材間は空洞にして、その代わり上の鋼材の底面と下の鋼材の上面に格子状の線を入れ、その交差点にバネ要素を取り入れて解析を回してみる。そのためまずは載荷面側の中央にバネをひとつだけ入っている状態のものを作ってみてうまく行くかを試してみる。今日はジオメトリでの作成を試みたがバネの部分の設定がうまくできていなく、メッシュが切れていなかったようで解析が回らなかったため、やり方がわかりそうな人に聞くなりしてみる。
縦軸:荷重 横軸:変位
ポアソン比が0に近い場合、仮に縦に荷重を加えても横に膨らんだりしにくくなるため、ヤング率が低いかつ、ポアソン比が小さい、つまりスポンジのような仮想材料を用いることで、仮想材料で下の鋼材を押してしまうというような状況がないようにしようとした。
仮想材料のポアソン比を0.001にし、解析を回したら、想定通りほぼ鋼材が接触しているような見た目になったが、数値的な結果としてグラフは変化が得られなかった。
仮想材料をもっと柔らかいものにするために、仮想材料のヤング率を0.01にして、ポアソン比を0.001で解析を回したら、上の鋼材が下の鋼材をすり抜けてしまった。前回とは違い、スケールファクターは特にいじっていないく、下の鋼材は挙動をほんの少ししか示していなく、数値的にもほぼ変化がなかったため完全にすり抜けてしまっていた。
現在は間の空いた2枚の部材の片側を降伏させて、荷重の様子を段階的に確認していった時、上の鋼材が降伏応力を迎えた後、下の鋼材に接触して次は下の鋼材が降伏するという状況を再現したく、加えている荷重と鉛直方向の変位のグラフが2段階にわけて降伏している様子が見られるグラフを作成しようとしている。(旭川での実験結果のようなグラフ 図1)しかし上の鋼材が降伏していく際、一緒になって下の鋼材も少しずつ降伏してしまっている。そのためグラフが一回分の降伏しか確認できていないと思われる。
縦軸:荷重 横軸:変位
設定荷重が3.526Nだとあまり降伏が見られなかったため、荷重を大きくしていった結果、10Nまで荷重を加えることができたがそれ以上はエラーが出てしまった。
タイムステップの数も10分割から20分割に変更。
結果的に降伏は確認することができたものの1回分の降伏しか確認することができなかった。下の鋼材の変形が確認できたものの、降伏にまでは至っていないと思われるため、もう少し荷重が加えられるように設定を変えてみたい。
たわみの理論値計算がミスっていた
訂正 33.801→3.3801
仮想材料の大きさが大きく変わるため結果が変わるはず。
モデル図 鋼材 200×130×9 (上部、下部の部材)
仮想材料 200×130×3.3801 (中間の部材)
ヤング率 ポアソン比
鋼材 235 0.3
仮想材料 1 0.3
設定荷重 3.526N(面載荷 上部鋼材の断面のみ)
○前回のモデルの変更点
・線荷重から載荷側の上の鋼材の断面による面荷重に
・設定荷重を増やした
・理論値をしっかり仮想材料も考慮したものへ
設定荷重を増やして解析を回したが、設定荷重を理論値の3倍以上にすると、エラーが出てしまった。
Arrêt suite à l'échec de l'intégration de la loi de comportement. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. ! ! ! ! Conseils : ! ! - Vérifiez vos paramètres, la cohérence des unités. ! ! - Essayez d'augmenter ITER_INTE_MAXI, ou de subdiviser le pas de temps localement via ITER_INTE_PAS.
このエラーによりITER_INTE_MAXIを大きくすればいいということだと思ったが、この値を何度か変え解析を回してみてもエラーが出てしまった。
設定荷重を2倍にしたときは解析が回った。しかし下の鋼材の外見の降伏を見ることはできなかった。
スケールファクター 20倍
スケールファクター 25倍
スケールファクター 30倍
まず簡単なモデルで2段階の降伏が見られるグラフを作成できるかを試してみることになった。
・鋼材 200(高さ)×130(幅)×9(厚さ)
仮想材料 200×130×34.232(理論値)
ヤング率 ポアソン比
鋼材 20600 0.3
仮想材料 1 0.3
しかし今回出たグラフは直線になってしまった。(縦軸 荷重 横軸 変位)
一見Paravisのスケールファクターが20倍のものをみたら良さげに見えたが、それ以降の倍率を見たところ上の鋼材が下の鋼材を貫通してしまっているため、設定の仕方が良くなかったと思われる(貫通させないために仮想材料を入れたはずだったのに意味がなくなってしまっている。というか仮想材料は貫通していないのになぜ鋼材だけ貫通しているのか。)。そもそも今回このモデルの鋼材1枚のみの理論値で考えてしまっていたため計算し直す必要がある。
荷重方法が今回は線荷重にして、荷重部分のグラフを作成したが、本当にそれでいいのか(→上部鋼材の載荷部の断面の面荷重へ)と、計算の仕方があっているのかの確認もする。
あと仮想材料をParavisで表示させない方法も調べておきたい。→ExtractGroupから表示させたいグループのみを選択して反映。
左のグラフが過去の実験結果を示したグラフで右が解析結果によるグラフ。
仮想材料を用いても降伏が一回しか見られないという小川さんの結果を確認することができた。
前回までのモデルで相当応力−相当ひずみ曲線を作成した。上のモデル図はSIEQ_NOEUのミーゼス応力を表示しxが0.01の箇所(固定面側)でスライスしたもの。
前回の応力−ひずみ曲線はマイナスの値を取っていたり、与えていたはずの応力よりも圧倒的に早く降伏してしまっていた。改善のためまずマイナスでなくなるように絶対値を用いる相当応力と相当ひずみを使用することになった。
Paravisで相当ひずみを確認するためにAsterStudyで設定を付け加える必要があった。まずPost ProcessingのCLAC_CPAMPよりCRITERES(基準値)のところで以前はSIEQ_NOEU(相当応力)のみだったが、ここにEPEQ_NOEU(相当ひずみ)を加えた。そしてOutputも同様にEPEQ_NOEUを加えることでParavis で相当ひずみを確認することができるようになる。
相当応力−相当ひずみ曲線を作成した際、スライスした箇所は固定面側の面をスライスしたがxが0の箇所ではスライスができないためxが0.01の箇所でスライスした。前回は断面の9箇所のグラフを作成していたが、今回はスライスした断面の上部と下部の中央の点の2箇所のみとして(それ以外はあまり意味がないため)2つのグラフを作成した。結果としてしっかり設定荷重(238MPa)で降伏するグラフを得ることができた。
卒論に関しては、以前までは「Atype」と「Btype」と書かれていた過去の似た内容の卒論をしていた小川さんのデータを参考にさせてもらってモデルを作成しようとしていたが、今回の新しいモデルで必要だった内鞘に関する情報がないモデルで設計図にも内鞘のサイズなどに関する情報がなかったため、そこで止まってしまっていたが、先日「Ctype」という内鞘の使用されているモデルのデータを見つけてもらったため、まずこのモデルを自分の使用しているパソコンで解析が回るかを試し、内鞘が2段階に降伏するため応力−ひずみ曲線は二段階に降伏するものが得られるはずだからその確認をしてみようとなった。
当然であったが15分程度では解析が回らず、設定時間が足りないというエラーが出てしまったので45分で試したが同様のエラーが出てしまったため、10時間に設定し次の日に確認しようとしたがデータが飛んでしまっていたため、もう一度解析を回して、明日確認し続きを行ってみようと考えている。
https://www.str.ce.akita-u.ac.jp/~gotouhan/j2023/hattori23/応力para.png
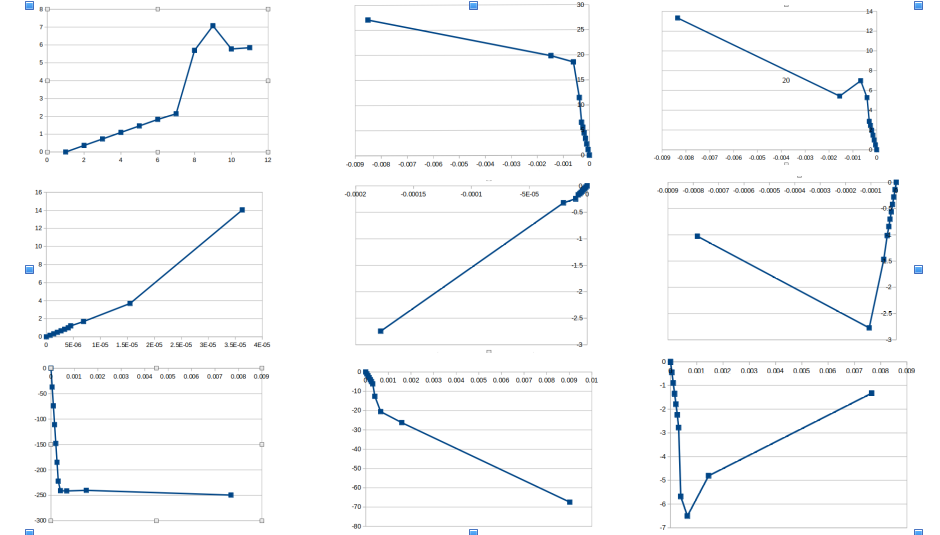
上記の写真が今回使用した片持ちばりの載荷されている様子の写真で、このモデルの最もひずみが見られる箇所をスライスしてプロットした点から作った応力−ひずみ曲線が上記のグラフのようになった。
応力がマイナスになっているのは圧縮、プラスになっているのは引張が働いているからだと思われる。paravisの設定をミーゼス応力で見ると応力が絶対値で見ることができる(ミーゼス応力はスカラー量であり、応力の方向を示さないため)。
先週作っていたモデルをecro_lineを用いた設定の仕方でも作成してみた。 弾塑性解析で作ったモデルをParavisで設定する方法等を練習。載荷面の9箇所等、特定のポイントそれぞれの応力−ひずみ曲線のグラフを作成するためにPlot Selection Over timeを用いた設定方法を覚えた。 小川さんのモデルをParavisで見る時、どのように応用できるか知るために行ってきたが、設定を理解するのにかなり時間がかかってしまったため(というかまだしっかりは理解しきれていない)まだtimeの数値を変えたもののグラフを作成したりはできていないため行ってみる。また、後藤先生に送ってもらった新しいモデルの図面は限界まで拡大したら蛍光色で書かれていた文字も読むことができた。
これは載荷面の右上端の点のものだが、上記のようなグラフになってしまった。今回、特に理由はなく載荷面をスライスしていたため、ひずみの最も変化のある箇所をスライスしてみてやったら、というアドバイスをもらったから試してみる。
・やったこと
小川さんの卒論のスライドや概要の内容を読んだ。そして卒論などで使っていたと思われるサロメのデータを使わせてもらって、自分の使っているパソコンで解析が回るかの確認。 解析は回ったが、弾塑性の内容についてよくわかっていなかったため、とりあえず弾塑性の春課題にあった簡単な形状の100×20×10のモデルを設定の仕方などの確認の意味もこめて作成して解析を回してみた。
salome-meca 弾塑性解析(2021)
C種について
https://www.mlit.go.jp/notice/noticedata/sgml/070/79000132/ref/y0000002.pdf
メモ
・10*5*700 単純1次
鉛直1次 理論値 37.15451
| メッシュ | 要素数 | 解析値 | 相対誤差 |
| 0.7 | 604706 | 37.8469 | 1.864 |
| 1 | 150957 | 39.3168 | 5.820 |
| 2 | 21270 | 47.7953 | 28.639 |
| 4 | 2609 | 75.567 | 103.386 |
鉛直2次 理論値 120.3942
| メッシュ | 要素数 | 解析値 | 相対誤差 |
| 0.7 | 604706 | 122.609 | 1.840 |
| 1 | 150957 | 127.365 | 5.790 |
| 2 | 21270 | 154.866 | 28.632 |
| 4 | 2609 | 244.558 | 103.131 |
鉛直3次 理論値 251.1547
| メッシュ | 要素数 | 解析値 | 相対誤差 |
| 0.7 | 604706 | 255.685 | -1.804 |
| 1 | 150957 | 265.629 | -5.763 |
| 2 | 21270 | 322.8 | 28.526 |
| 4 | 2609 | 509.496 | 102.861 |
水平1次 理論値 74.30902
| メッシュ | 要素数 | 解析値 | 相対誤差 |
| 0.7 | 604706 | 74.1075 | 0.271 |
| 1 | 150957 | 74.9296 | 0.835 |
| 2 | 21270 | 77.9669 | 4.923 |
| 4 | 2609 | 87.7007 | 18.022 |
水平2次 理論値 240.7885
| メッシュ | 要素数 | 解析値 | 相対誤差 |
| 0.7 | 604706 | 239.837 | 0.395 |
| 1 | 150957 | 242.486 | 0.705 |
| 2 | 21270 | 252.306 | 4.783 |
| 4 | 2609 | 283.626 | 17.791 |
水平3次 理論値 502.3093
| メッシュ | 要素数 | 解析値 | 相対誤差 |
| 0.7 | 604706 | 499.386 | 0.582 |
| 1 | 150957 | 504.892 | 0.514 |
| 2 | 21270 | 525.213 | 4.560 |
| 4 | 2609 | 590.132 | 17.484 |
共振周波数解析について
振動設計について
https://www.fml.t.u-tokyo.ac.jp/lecture/handout/DE/yurenu/2019vibra1.pdf
メモ
・Texで図を挿入する際に一段に2つ以上横に並べて図を貼る方法
\begin{figure}[h]
\begin{tabular}{cc}
%---- 最初の図 ---------------------------
\begin{minipage}{0.45\hsize}
\begin{center}
\includegraphics[width=サイズ]{ファイル1}
\caption{キャプション1}
\label{ラベル1}
\end{center}
\end{minipage} &
%---- 2番目の図 --------------------------
\begin{minipage}{0.45\hsize}
\centering
\includegraphics[width=サイズ]{ファイル2}
\caption{キャプション2}
\label{ラベル2}
\end{center}
\end{minipage}
%---- 図はここまで ----------------------
\end{tabular}
\end{figure}
図がかぶってしまうときは[width]のサイズを変えたりする。
今回は2つを横に並べただけで試していないがおそらく\begin{tabular}{cc}のccの数を増やすことで並べる図の数を変更できると思う。
参考文献
http://www.yamamo10.jp/~yamamoto/comp/latex/make_doc/insert_fig/index.php
・texで表を作成した際に全体のサイズを変更する方法
→\scalebox で拡大・縮小する
\begin{table}[htbp]
\begin{center}
\caption{表題}
\label{heading}
\scalebox{0.5}[0.9]{ %ココ
\begin{tabular}{|c|c|c|c|} \hline
& & & \\\hline
& & & \\\hline
\end{tabular}
}
\end{center}
\end{table}
通常のグラフを作成して\label{heading}の後に\scalebox{0.5}[0.9]{ を入れ、\end{tabular}の後、}で閉じる。
\scaleboxの後ろの{}で横倍率、[]で縦倍率が変更可能。ただ、[]は省略可能で、今回は{}のみで試したがうまく行った。
参考文献
https://blog.goo.ne.jp/shafact/e/8219383eb299d5b6bdfd1544d546df9f
・texでの矩形選択とコピペ方法
Escを押した後、Ctrl+vで矩形選択モードになり矢印キーで選択。
選択したい箇所が決まったら、yでコピー。
その後、pで貼り付けるが、この時下の列に注意。貼り付ける時、挿入箇所から縦に無理やり挿入されるから、下に文章があるとその文章に割り込んだ形になるため、事前にスペースキーなどで列を揃えておく必要がある。
表を作成する際、メモを開いて
%\begin{figure}[h] ←これはいらない
%1 & \\
%2 & \\
%3 & \\
%4 & \\
%5 & \\
%6 & \\
%7 & \\
%8 & \\
%9 & \\
%1 & \\
的なものを用意してtexに作成する表のしたに貼り付けておくとかなり便利でした。
他にも表を多用する際は一度メモに使用するコマンドを貼り付けておき、そこからコピペすることでかなり時短になりました。ただ、これでも大量に表を作成すると時間はかかります。他にいい方法があるか今後探してみます。というかスクショを使えるときは絶対その方が楽です。
texの基本的な書き方https://www.str.ce.akita-u.ac.jp/~gotou/linux/gotouimes.txt参照
| メッシュの長さ | 要素数 | 先端変位[mm] | 相対誤差 | 計算者 |
| 0.7 | 155192 | 0.08378905246 | 15.365 | 安藤 |
| 0.8 | 138808 | 0.08380386491 | 15.350 | 安藤 |
| 0.9 | 82587 | 0.083707073981 | 15.45 | 兼田 |
| 1.1 | 38671 | 0.084201207602 | 14.95 | 兼田 |
| 1.2 | 31929 | 0.083688 | 15.466. | 柴田 |
| 1.3 | 28621 | 0.083669 | 15.4857 | 柴田 |
| 1.4 | 28854 | 0.08368 | 15.47 | 佐藤 |
| 1.5 | 20015 | 0.084052 | 15.10 | 佐藤 |
| 1.6 | 19448 | 0.0835402938 | 15.62 | 皆川 |
| 1.7 | 13801 | 0.0834355098 | 15.72 | 皆川 |
| 1.8 | 12528 | 0.083733 | 15.42 | 永山 |
| 1.9 | 11769 | 0.083924 | 15.23 | 永山 |
| 2 | 10699 | 0.084076876559 | 15.074 | 辻 |
| 3 | 3579 | 0.08414561753 | 15.004 | 辻 |
| 4 | 1628 | 0.082794 | 16.37 | 服部 |
| 5 | 1016 | 0.083033 | 18.89 | 服部 |
| 6 | 839 | -0.082882 | 16.26 | 梶原 |
| 7 | 554 | -0.080871 | 18.28 | 梶原 |
| 8 | 285 | 0.079995 | -19.20 | 工藤 |
| 9 | 261 | 0.078980 | -20.22 | 工藤 |
| 10 | 232 | 0.081911 | 17.26 | 佐々木 |
| 11 | 208 | 0.075676 | 23.56 | 佐々木 |
異方性1次について
自分のデータ
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 4 | 1500 | 0.430156 | 12.52 | 服部 |
| 5 | 432 | 0.282968 | 42.45 | 服部 |
全員のデータ
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差 | 計算者 |
| 0.7 | 144563 | 0.505252 | 2.76 | 安藤 |
| 0.8 | 141517 | 0.504692 | 2.64 | 安藤 |
| 0.9 | 91648 | 0.502595 | 2.216 | 兼田 |
| 1.1 | 27160 | 0.489914 | 0.363 | 兼田 |
| 1.2 | 24675 | 0.487088 | 0.791 | 柴田 |
| 1.3 | 23446 | 0.4868010 | 0.995 | 柴田 |
| 1.4 | 17738 | 0.485999 | 1.16 | 佐藤 |
| 1.5 | 15438 | 0.485180 | 1.33 | 佐藤 |
| 1.6 | 15900 | 0.483286 | 1.71 | 皆川 |
| 1.7 | 12142 | 0.477952 | 2.80 | 皆川 |
| 1.8 | 11604 | 0.482085 | 1.9554 | 永山 |
| 1.9 | 10391 | 0.470887 | 4.2329 | 永山 |
| 2 | 10291 | 0.480910 | 2.19 | 辻 |
| 3 | 2328 | 0.431937 | 12.15 | 辻 |
| 4 | 1500 | 0.430156 | 12.52 | 服部 |
| 5 | 432 | 0.282968 | 42.45 | 服部 |
| 6 | 356 | 0.3441556 | 30.00 | 梶原 |
| 7 | 196 | 0.213934 | 56.49 | 梶原 |
| 8 | 104 | 0.229874 | 53.25 | 工藤 |
| 9 | 81 | 0.232308 | 52.75 | 工藤 |
| 10 | 78 | 0.203271 | 58.65 | 佐々木 |
| 11 | 63 | 0.222316 | 54.78 | 佐々木 |
等方性2次について
自分のデータ
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 4 | 1500 | 0.429254 | 3.01 | 服部 |
| 5 | 432 | 0.428170 | 2.75 | 服部 |
全員のデータ
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差 | 計算者 |
| 0.7 | 144563 | 0.430124 | 3.22 | 安藤 |
| 0.8 | 141517 | 0.430132 | 3.22 | 安藤 |
| 0.9 | 91648 | 0.430020 | 3.197 | 兼田 |
| 1.1 | 27160 | 0.429828 | 3.151 | 兼田 |
| 1.2 | 24675 | 0.429836 | 3.15 | 柴田 |
| 1.3 | 23446 | 0.42974 | 3.13 | 柴田 |
| 1.4 | 17738 | 0.429797 | 1.3 | 佐藤 |
| 1.5 | 15438 | 0.429958 | 3.14 | 佐藤 |
| 1.6 | 15900 | 0.429755 | 3.18 | 皆川 |
| 1.7 | 12142 | 0.429676 | 3.11 | 皆川 |
| 1.8 | 11604 | 0.429829 | 3.1507 | 永山 |
| 1.9 | 10391 | 0.429684 | 3.1159 | 永山 |
| 2 | 10291 | 0.429620 | 3.10 | 辻 |
| 3 | 2328 | 0.429169 | 2.99 | 辻 |
| 4 | 1500 | 0.429254 | 3.01 | 服部 |
| 5 | 432 | 0.428170 | 2.75 | 服部 |
| 6 | 356 | 0.428452 | 2.82 | 梶原 |
| 7 | 196 | 0.42591 | 2.21 | 梶原 |
| 8 | 104 | 0.426074 | 2.25 | 工藤 |
| 9 | 81 | 0.425552 | 2.12 | 工藤 |
| 10 | 78 | 0.488382 | 17.20 | 佐々木 |
| 11 | 63 | 0.423972 | 9.0534 | 佐々木 |
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差 | 計算者 |
| 0.7 | 1455234 | 0.422484 | 1.388 | 安藤 |
| 0.8 | 142973 | 0.422570 | 1.409 | 安藤 |
| 0.9 | 91648 | -0.420437 | 0.897 | 兼田 |
| 1.1 | 27160 | -0.405618 | 2.659 | 兼田 |
| 1.2 | 24675 | 0.404349 | 2.96 | 柴田 |
| 1.3 | 23446 | 0.404185 | 3.00 | 柴田 |
| 1.4 | 17738 | 0.398604 | 4.34 | 佐藤 |
| 1.5 | 15438 | 0.396593 | 4.83 | 佐藤 |
| 1.6 | 16122 | 0.398212 | 4.44 | 皆川 |
| 1.7 | 12026 | 0.393411 | 5.59 | 皆川 |
| 1.8 | 11604 | 0.393668 | 5.53 | 永山 |
| 1.9 | 10391 | 0.390695 | 6.24 | 永山 |
| 2 | 10921 | -0.395103 | 5.18 | 辻 |
| 3 | 2328 | -0.324762 | 22.06 | 辻 |
| 4 | 1500 | -0.155013 | 62.80 | 服部 |
| 5 | 432 | -0.065278 | 84.33 | 服部 |
| 6 | 357 | 0.213062 | 48.87 | 梶原 |
| 7 | 196 | 0.1019 | 75.55 | 梶原 |
| 8 | 104 | 0.1158624 | 72.20 | 工藤 |
| 9 | 81 | 0.1255118 | 69.88 | 工藤 |
| 10 | 78 | -0.07733 | 81.44 | 佐々木 |
| 11 | 63 | -0.1999 | 52.03 | 佐々木 |
すいません、僕のデータの相対誤差が100倍し忘れていたので直してあります。
| メッシュ長さ | 要素数 | 先端変位(4隅の平均値)[mm] | 相対誤差 | 計算者 |
| 0.7 | 198464 | 6.54281 | -1.91 | 安藤 |
| 0.8 | 113812 | 6.5104 | -2.39 | 安藤 |
| 0.9 | 40280 | 6.3631525 | -4.60 | 兼田 |
| 1.1 | 30055 | 6.3363525 | -5.00 | 兼田 |
| 1.2 | 264667 | 6.3043375 | 5.48 | 柴田 |
| 1.3 | 25180 | 6.304355 | 5.48 | 柴田 |
| 1.4 | 32212 | 6.31612 | 5.31 | 佐藤 |
| 1.5 | 17753 | 6.1209 | 8.23 | 佐藤 |
| 1.6 | 14296 | 6.2044625 | -6.98 | 皆川 |
| 1.7 | 13596 | 6.2156625 | -6.81 | 皆川 |
| 1.8 | 2866 | 5.737755 | -13.98 | 永山 |
| 1.9 | 6001 | 5.7263625 | -14.15 | 永山 |
| 2 | 5617 | 5.6458525 | -15.355 | 辻 |
| 3 | 2309 | 5.4728755 | -17.948 | 辻 |
| 4 | 617 | 3.6160575 | 45.12 | 服部 |
| 5 | 494 | 3.8580375 | 42.16 | 服部 |
| 6 | 581 | 2.50682 | -62.416 | 梶原 |
| 7 | 133 | 1.41225 | -78.82 | 梶原 |
| 8 | 78 | 1.2887175 | -80.68 | 工藤 |
| 9 | 72 | 1.2879925 | -80.69 | 工藤 |
| 10 | 60 | 1.14344 | -82.85 | 佐々木 |
| 11 | 65 | 1.23124 | -81.154 | 佐々木 |
pwd : 自分の位置
ls : すべてのファイルを確認する
mkdir : 新規ファイルの作成 ls (作成できているかの確認)
cd ファイル名 :複数のファイルから特定のファイルに入る pwd (現在位置の確認)
ls -a : 隠しファイル
gedit ファイル名.tex & : ファイルを作りそのファイルに入るorもともとあるファイルに入る
vi ファイル名.tex : 編集(作業スペースからファイル内容を) Esc → : → wq : 内容保存
cp コピーしたいファイル名.tex 新しいファイル名.tex : 新しいファイルに違うファイルの内容をコピー)
rm ファイル名.tex : ファイルを消す
cd .. : 1つ前のフォルダに戻る(他ファイルの選択が可能に)
rmdir ファイル名 :mkdirで作ったものの削除
マウスの両クリックor中央クリック : 選択した文章コピーand貼り付け
http://dugi6514.odns.fr/doc/v15/en/index.php?man=commande
https://www.slideshare.net/slideshow/salomemeca-59878666/59878666
https://qiita.com/Jun_Tatsuno/items/3e6558c1adc4dd9499fe
PARM_THETA によって,θ の値を変えられる. 時間と空間の再分割時の不整合に注意
RESI_INTE_RELA, ITER_INTE_MAXIについて
「これらは線形研究のパラメータである。最大反復回数は、線形研究の収束を行うため と、線形研究の収束のために到達すべき精度reslin が与えられる。接触 を使用しないことを推奨する。 CORD法では、精度や反復回数をあまり高く指定する必要はありません。 実践によると、線形研究の反復は 2、3 回で十分です。したがって デフォルトの精度で3回の反復を求めることで満足できる。ユーザーは999 を超える線形調査の反復を行うことはできません。 一方、MIXED法では、損傷のある問題では、数十回の反復が有効です。 が有効です。」 Deepl翻訳より
サンドイッチ梁について
AsterStudyでよく使うコマンド
| コマンド名 | 使用用途 | カテゴリーの名前 |
| LIRE_MAILLAGE | メッシュの選択 | mesh |
| AFFE_MODELE | モデル形状の指定 | model Definition |
| DEFI_MATERIAU | 材料諸量の指定 | material |
| AFFE_MATERIAU | 各モデルの材料諸量の指定 | material |
| DEFI_FONCTION | 時間の指定 | Functions and Lists |
| DEFI_LIST_REEL | 時間ステップの指定 | Functions and Lists |
| AFFE_CHAR_MECA | 境界条件の指定 | BC and Load |
| DEFI_CONTACT | 摩擦なしの接触の指定 | BC and Load |
| STAT_NON_LINE | 非線形解析の設定 | Analysis |
| CALC_CHAMP | 計算の指定 | Post processing |
| IMPR_RESU | 出力の指定 | output |
Arrêt suite à l'échec de l'intégration de la loi de comportement. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. ! ! ! ! Conseils : ! ! - Vérifiez vos paramètres, la cohérence des unités. ! ! - Essayez d'augmenter ITER_INTE_MAXI, ou de subdiviser le pas de temps localement via ITER_INTE_PAS.
ITER_INTE_MAXIの値を大きくしてみる。(ただ大きくすればいいというわけではない?)RESI_CPLAN_RELA, ITER_CPLAN_MAXI, RESI_INTE_RELA, ITER_INTE_MAXIにチェックを入れてみた。 ITER_INTE_PASを考慮するでも解決するらしい(未検討 調べたところ、CONVERGENCEの設定のところにあると思われたが、見つからずよくわからなかった。用いることで、局所的に時間ステップを細分化することができるらしい。)
! <NonConvergenceError> <MECANONLINE9_7> !
! ! ! Arrêt pour cause d'absence de convergence avec le nombre d'itérations requis dans l'algorithme non-linéaire de Newton. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. ! ! ! ! Conseils : ! ! - Augmentez ITER_GLOB_MAXI. ! ! - Réactualisez plus souvent la matrice tangente. ! ! - Raffinez votre discrétisation temporelle. ! ! - Essayez d'activer la gestion des événements (découpe du pas de temps par exemple) dans la commande DEFI_LIST_INST.
! ニュートンの非線形アルゴリズムにおいて、必要な反復回数で収束しなかったため停止した! ! グローバルデータベースが保存される。停止前のステップが保存されている! ! ! ! アドバイス: ! ! - ITER_GLOB_MAXI を増やす! ! - タンジェント行列の更新頻度を上げる! ! - 時間離散化を洗練させる ! ! - DEFI_LIST_INSTコマンドでイベント管理(例えば時間ステップの切断)を有効にしてみてください。
! <EXCEPTION> <FACTOR_11> ! ! ! ! Problème : la matrice est singulière ou presque singulière : ! ! Lors de la factorisation de la matrice, on a rencontré un problème ! ! (pivot nul ou presque nul) à la ligne 12414 qui correspond au degré de liberté donné ci-dessus. ! ! ! ! Risques et conseils : ! ! * Si la ligne correspond a un degré de liberté physique, il s'agit probablement d'un mouvement ! ! de corps rigide mal bloqué. ! ! Vérifiez les conditions aux limites. ! ! Si vous faites du contact, il ne faut pas que la structure ne "tienne" que par le contact. ! ! Vérifiez également les caractéristiques matériaux (module d'Young, ...). ! ! ! ! * Si la ligne correspond a un degré de liberté de Lagrange, il s'agit sans doute d'une condition ! ! limite redondante. ! ! En particulier, il se peut que la relation linéaire surabondante provienne des conditions de contact. ! ! Peut-être devriez vous exclure certains noeuds des conditions de contact ! ! (mots clés SANS_NOEUD et SANS_GROUP_NO). ! ! ! ! * Si le solveur utilisé est LDLT ou MULT_FRONT, vous pouvez utiliser le solveur MUMPS ! ! car celui-ci est le seul à pouvoir factoriser les matrices qui ne sont pas définies positives. ! ! ! ! * Parfois, en parallèle, le critère de détection de singularité de MUMPS est trop pessimiste ! Il reste néanmoins souvent ! ! possible de faire passer le calcul complet en relaxant ce critère (augmenter de 1 ou 2 la valeur du mot-clé NPREC) ou ! ! en le débranchant (valeur du mot-clé NPREC=-1) ou en relançant le calcul sur moins de processeurs. ! ! ! ! * Il se peut aussi que ce phénomène soit tout à fait normal avec X-FEM si la fissure passe ! ! très près d'un noeud. ! ! Si le nombre de décimales perdues n'est pas trop grand (max 10 décimales), ! ! vous pouvez relancer le calcul en augmentant le nombre de décimales perdues autorisé : ! ! mot-clé NPREC du mot clé facteur SOLVEUR. ! ! Sinon, contactez l'équipe de développement. !
・サロメの過去の人のデータをコピーする際はRun_Caseも一緒にコピーすると、Asterstudyの解析結果も確認することができる
・最大主応力と最小主応力について
物体に力が作用するときに方向によりせん断力がゼロになる面が必ず存在しそのときの垂直応力を主応力と呼び直交する2方向の主応力のうち大きい方を最大主応力、小さい方を最小主応力といい、通常+が引張りで-が圧縮となる。
ParavisではPRIN_1が最小主応力 PRIN_3が最大主応力
最大主応力は引張応力、最小主応力は圧縮応力となる。
尚、最大主応力の結果表示でプラスの値を示す場合は、引張応力
マイナスを示す場合は、圧縮応力
最小主応力の結果表示でプラスの値を示す場合は、引張応力
マイナスを示す場合は、圧縮応力
↑実際にParavisで確認しながらやると理解しやすい
・最小主ひずみ、最大主ひずみについて
最大主ひずみは材料にかかる最大の引張りひずみの評価、最小主ひずみは最大の圧縮ひずみの評価に使用される
・appariementについて
ジオメトリ上の固定点ループのパラメータ(デフォルト・パラメータ)は、§3.4.1 に示されている。 § 3.4.1 . ALGO_RESO_ GEOM = 'NEWTON'を選択すると、一般化ニュートンアルゴリズムに切り替わります。 幾何学的非線形性は、各ニュートン反復で考慮され、マッチングがやり直され、局所基底(法線と接線)が再計算されます。このモードでは、幾何学的基準の評価に対応する追加の列が収束表に表示される(CONTACT NEWTON列)。 (コンタクト・ニュートン(CONTACT NEWTON GENE CRIT. GEOM.)列)。 Les paramètres de la boucle de point fixe sur la géométrie (paramètre par défaut) sont donnés dans le § 3.4.1 . Quand on choisit ALGO_RESO_ GEOM ='NEWTON', on bascule vers l'algorithme de Newton généralisé. La non-linéarité géométrique est alors prise en compte à chaque itération de Newton : on refait l'appariement et on recalcule la base locale (normale et tangentes). Dans ce mode, une colonne supplémentaire apparaît dans le tableau de convergence, elle correspond à l'évaluation du critère géométrique (colonne CONTACT NEWTON GENE CRIT. GEOM.).
・ペナルティ要素(法)について https://www.cybernet.co.jp/ansys/learning/glossary/penaltyhou/
・岐阜高専さんのページ
http://opencae.gifu-nct.ac.jp/pukiwiki/index.php?SALOME-Meca%A4%CE%BB%C8%CD%D1%CB%A1%B2%F2%C0%E2
・接触と摩擦について file:///home/kouzou/%E3%83%80%E3%82%A6%E3%83%B3%E3%83%AD%E3%83%BC%E3%83%89/12-contact-friction.pdf ・CLA https://www.sciencedirect.com/science/article/pii/S0045782518302561#bb29