![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
柴田真杜
主塔にも幾何学非線形を考慮する必要があるのか。
まずは2本モデルで実験値、ケーブルのみpositive、ケーブル+主塔positiveで比較した。
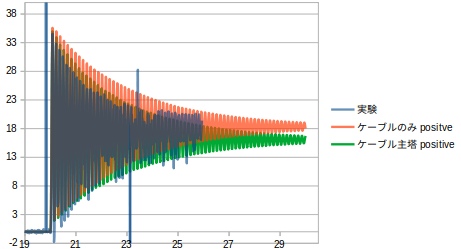
収束する値が実験値と近いのはケーブルのみpositiveのときであった。
静的解析を行い釣り合ったときの変位(静的変位)は、ケーブルのみpositiveの場合もケーブル主塔positiveの場合も18.335mmになるよう設定した。
したがって収束する値は18.335に近いはずだがケーブル主塔positiveの場合、動的解析にすると18.335mmより小さくなっている。
静的解析で釣り合い時の横方向変位、縦方向変位をみた
| 横方向変位 | 縦方向変位 | |
| ケーブルのみpositive | 13.4464mm | 0.0082mm |
| ケーブル主塔positive | 18.1894mm | 0.24mm |
主塔にも幾何学非線形を考慮することで変位は変化したが、縦方向の変位は依然として小さいため考慮しなくてもいい?
2本モデルでcable要素を使用し、解析を行った。ケーブルの分割数の影響を調べるため、分割数1と100の先端変位、張力を比較した。
次に4本モデルにおいてcable要素を使用して解析を行ったところ、ケーブルの分割数1だと正常に回ったが、100にすると破断後の挙動がおかしくなった。(この原因はまだ分かっていない)
cable1と2の材料特性、3と4の材料特性がそれぞれ同じためこれまではまとめて設定していた。これを各ケーブルごとに設定することで4本モデルでも分割数100で正常に回るようになった。
ケーブルに圧縮力が生じないようにする方法を調べたところ、材料を選ぶところでcable要素があった。
cable要素では圧縮時のヤング率を設定することができ、今回は圧縮を生じさせないため0.00001とした。(0にするとよくない?)
cable要素の設定を進める上で幾何学非線形をいれることになる。
幾何学非線形を考慮したい理由:幾何学非線形を考慮することで、破断後静止し釣り合ったとき鉛直軸と各ケーブルのなす角度が大きく変化する。この角度変化が変位などに影響を及ぼすから。
また、変形にともなった剛性の変化を考慮する必要があると考えるから。
幾何学非線形positiveとnegativeの先端変位を静的解析と計算の結果から比較した。
| 静的解析 | 計算 | |
| positive | 7.8mm | 7.6mm |
| negative | 8.67mm | 8.42mm |
幾何学非線形を入れたほうが先端変位が小さくなることを確認できた。
2本モデルで幾何学非線形を入れたとき(positive)と入れなかったとき(negative)の比較を行った。
先端変位とケーブル張力
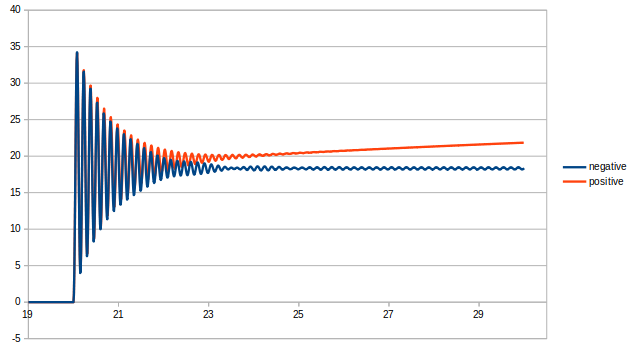
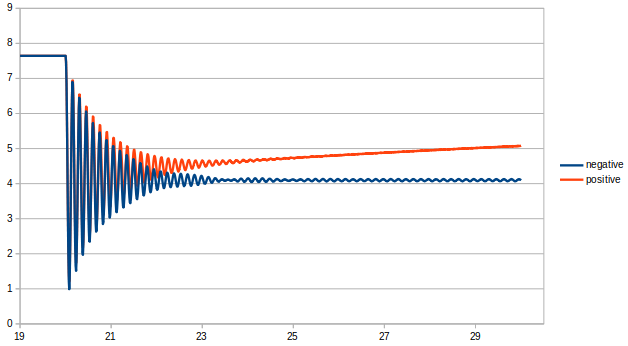
幾何学非線形をいれた場合、破断後のケーブル張力が収束せず大きくなり続けている。これに伴い先端変位も傾き続けている。
幾何学非線形の入れ方を間違っている可能性がある。
その理由としては、これまでの解析ではケーブルの初期張力が大きいでも小さいときでもケーブルの引張の剛性は変化しないと考えられる。
幾何学非線形を考慮することで、初期張力が大きくなる<と、引張の剛性も大きくなった解析を行うことが出来ると考えた。
まず、幾何学的非線形を考慮していないもの(negative)と考慮したもの(positive)の比較を行う。
条件の38で比較する。
先端変位
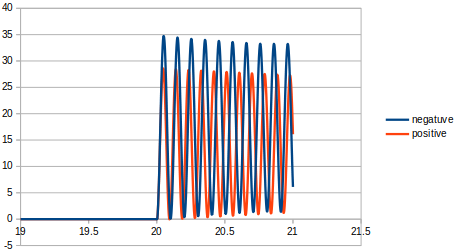
破断時のケーブル張力の変化量
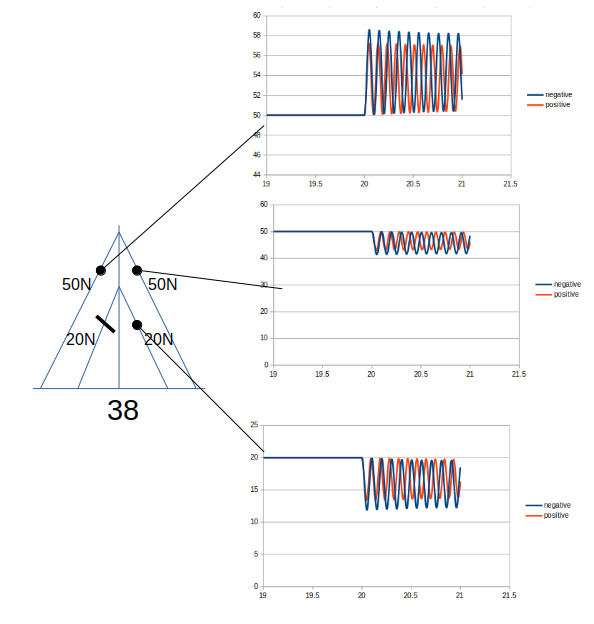 動き
動き


幾何学非線形を考慮したためケーブルの引張の剛性が高くなりそれによって先端変位が小さくなった?
またケーブルが曲がりにくくなり張力の変化量も小さくなった?
結果に影響が出たことから、解析方法の見直しが必要。
これまで2本モデルでは実験と解析一致していたが、幾何学非線形を考慮した解析と実験の解析も比較する必要がある。
4本モデルで初期張力がケーブル破断時の張力に与える影響をわかりやすくした。
ケーブル破断時の張力の変化量に違いがでるのは、ケーブル1,2と3,4で初期張力が異なるものを比較した時である。
ケーブル1,2と3,4で初期張力が異なるものでも張力の変化量が一致するpointもある。これは破断した隣のケーブル張力である。
ケーブル破断時の張力への影響を初期張力、ヤング率、破断するケーブル、サグの有無といったパラメータの内1つのみを変え比較する。
条件
主塔の材料特性
寸法:5mm \( \times \) 10mm \( \times \) 900mm
密度:7.668\( N/mm^{2} \) \( \times 10^{-9} \)
ケーブルの材料特性
直径:3.85mm
密度:3.13\( N/mm^{2} \) \( \times 10^{-10} \)
主塔には全てに同じ減衰を与える(Salomeの材料特性の部分のα、βを変えない)
まずは初期張力の条件を変え、それ以外の条件を同じにしたもの同士を比較し、初期張力が破断後のケーブル張力に与える影響を調べる。
比較するものの初期張力を1にする。(9では初期張力20Nなので、得られたケーブル破断時の張力の結果を20で割る。)
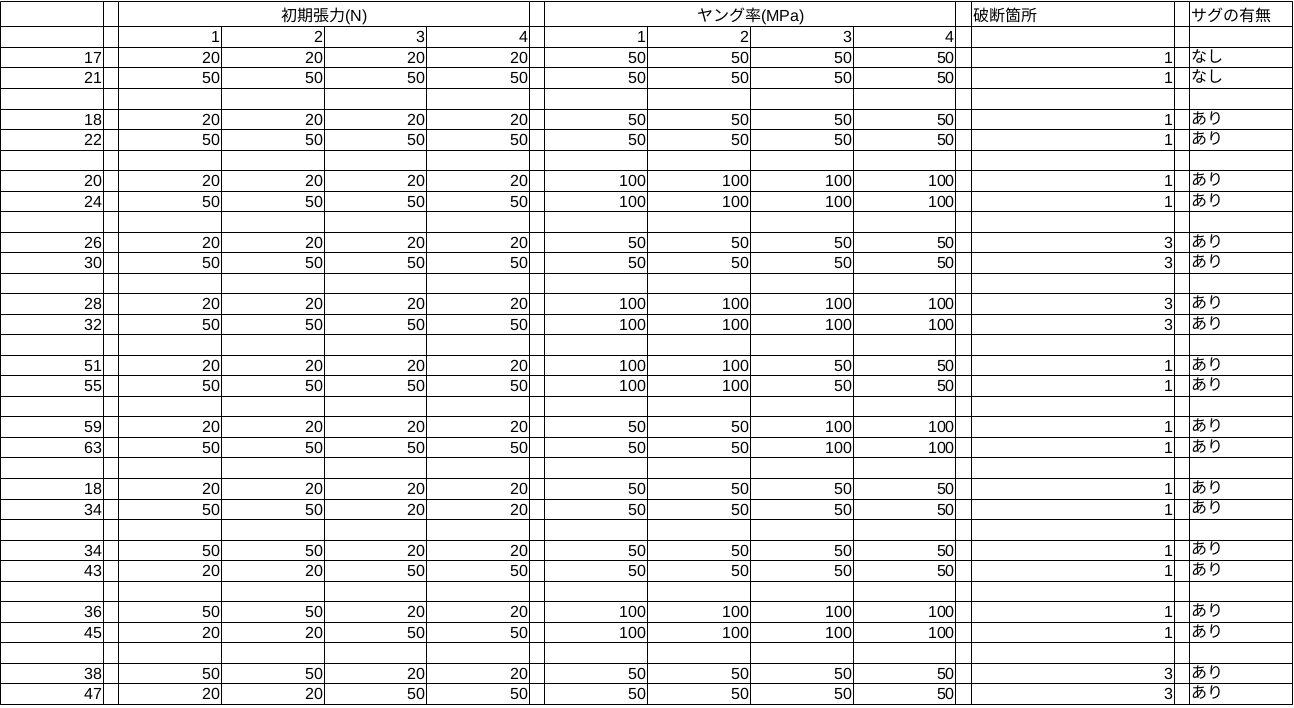
・2本モデル 9と13、10と14、12と16を比較
| 初期張力 | ヤング率 | サグ | |
| 9 | 20N | 50MPa | 無 |
| 13 | 50N | 50MPa | 無 |
| 10 | 20N | 50MPa | 有 |
| 14 | 50N | 50MPa | 有 |
| 12 | 20N | 100MPa | 有 |
| 16 | 50N | 100Mpa | 有 |

この結果より2本モデルにおいては、初期張力は破断後のケーブル張力に影響を及ぼさない。
・4本モデル
17と21、18と22、20と24、26と30、28と32、51と55、59と63、18と34、34と43、36と45、38と47を比較
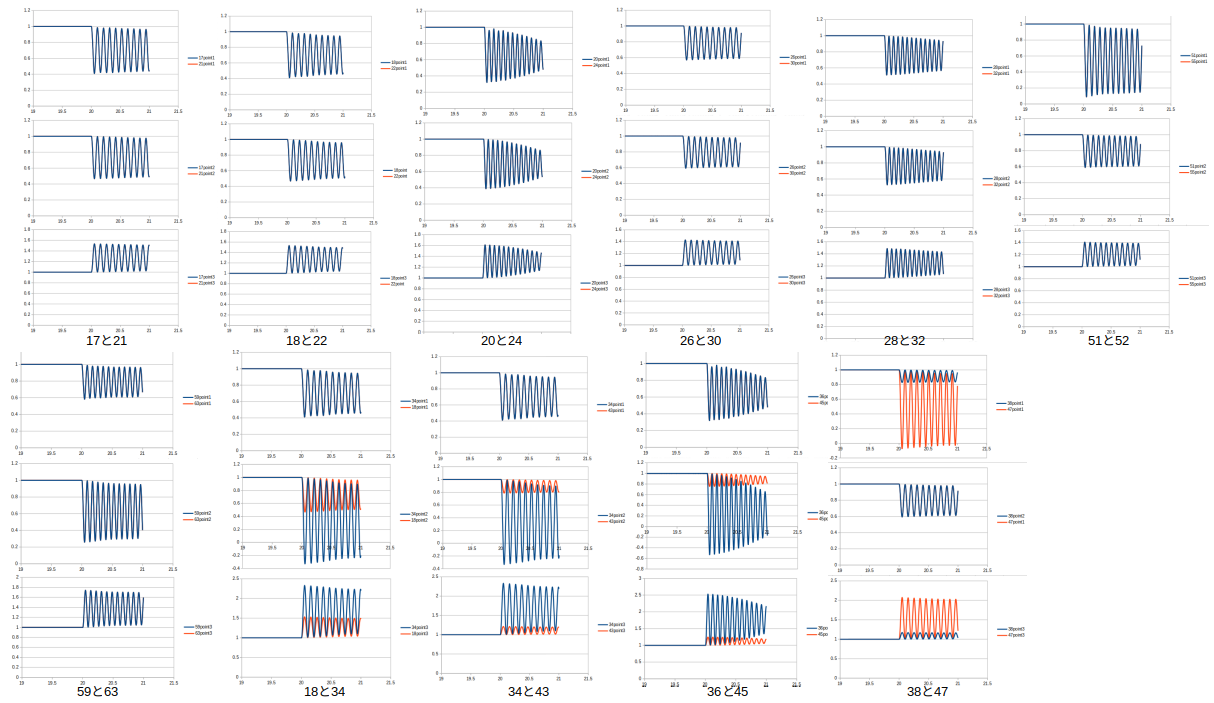
1〜4のケーブルで初期張力がそろっているものは(17など)初期張力の条件が異なるものを比較しても違いは見られなかった。
しかし1〜4のケーブルで初期張力がそろっていないものは(34など)破断後の張力の変化量に違いがでた。
6本モデル ケーブルのヤング率はすべて50N/mm2に設定
張力 上:28.70N 中:20.09N 下:11.48N
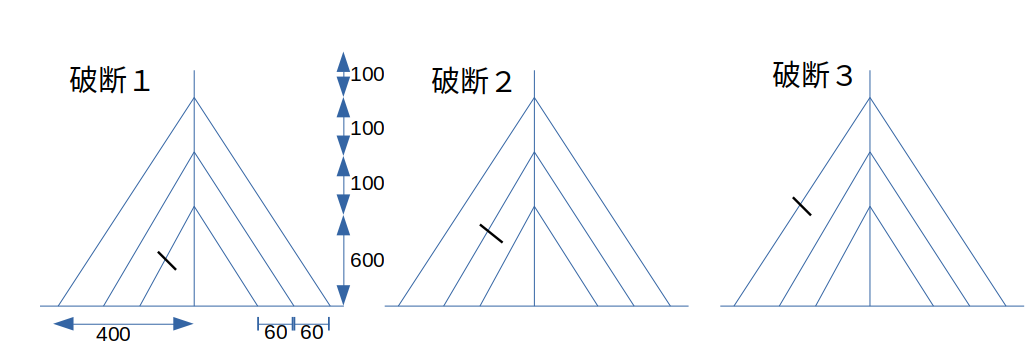
張力 上:28.71N 下:8.61Nは同じまま、ヤング率を上ケーブル80N/mm2、下ケーブル40N/mm2にして解析を行った。
張力の変化量
| ue_hidari | ue_migi | sita_hidari | sita_migi | (上の張力÷下の張力) |
| 4.608NN | -4.608N | - | -2.201 | 2.094 |
ケーブルのヤング率が変わることで破断時のケーブル張力の変化量比に影響が出ると考えられる。
ヤング率を全てのケーブルで50N/mm2と同じにしたときの塔の動きを確認する。このとき張力は上のケーブルが大きく、下のケーブルが小さくなるよう温度荷重を設定。その反対も
張力 上:28.71N 下:8.61N

ヤング率を同じにしても動きに違いはなかった。
張力の変化量
| ue_hidari | ue_migi | sita_hidari | sita_migi | (上の張力÷下の張力) | |
| 張力 上:28.71N 下:8.61Nのとき | 3.71N | -3.70N | - | -3.50N | 1.06 |
| 張力 上:14.35N 下:20.10Nのとき | 8.65N | -8.65N | - | -8.15N | 1.06 |
| 張力 上:14.3526N 下:14.3526Nのとき | 5.826N | 6.18N | - | 6.17N | 1.06 |
ケーブルのヤング率を揃えることで張力の変化量比に影響が出た。
ヤング率を100N/mm2に揃えたときの張力の変化量比は、1.03となった。
ヤング率を揃えると張力の変化量比は1.0に近づくと考えられる。
ヤング率を50N/mm2に揃えた時、張力の変化量比は1.06になった。
ヤング率を100N/mm2に揃えた時、張力の変化量比は1.11になった。
このことから、破断2の場合はヤング率を揃えると1.11に近づくと考えられる。
9月11日の実験モデルでケーブル張力の大小を上下逆にしてみた
張力 上:14.4081N 下:27.0556N
破断1

張力の大小を逆にしても違いはなかった。
張力の変化量
| ue_hidari | ue_migi | sita_hidari | sita_migi | (上の張力÷下の張力) | |
| 破断1 | 14.7217N | -14.7136N | - | -6.6275N | 2.218 |
| 破断2 | - | -12.8582N | 5.4554N | -5.4553N | 2.357 |
張力の大きさを上下で逆にしても、上下での張力の変化量の比がほぼ変化しない。(張力の入れ方は破断時のケーブル張力の変化量には影響しない)
実験モデル
張力 ケーブル上:24.0161N ケーブル下:15.7814N
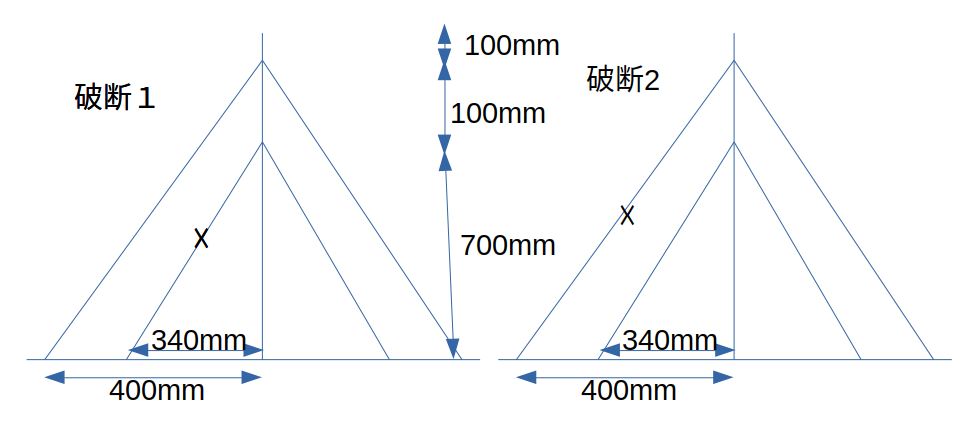
今までは先端変位を測定してDAFを求めてきた。しかし本数を増やしていくことで先端が最大変位にならない可能性がある。
今後は破断時の塔の動きを追うことで、ケーブル本数を増やした時の影響を評価していく。
モデル破断1の塔の動きは次のようになった。(ケーブル要素はアニメーションに映らないように設定。Scale Factorを1000にした。)

モデル破断2の塔の動きは次のようになった。(ケーブル要素はアニメーションに映らないように設定。Scale Factorを1000にした。)

破断時の張力の変化量
| ue_hidari | ue_migi | sita_hidari | sita_migi | (上の張力÷下の張力) | |
| 破断1 | 8.5869N | -8.5872N | - | -3.8658N | 2.221 |
| 破断2 | - | -21.43226N | 9.0947N | -9.09228N | 2.358 |
ケーブル1本、2本、4本のときで動きが異なることから、本数による影響もあると考えられる。
解析は健全時の変位がほぼ一致するように温度荷重を与えた。
実験と解析の結果
| 静的 | 動的 | 健全時 | DAF | |
| 実験 | 0 | 30.01 | 57.99 | 1.932 |
| 解析 | 0 | 30.00 | 59.20 | 1.973 |
ケーブル破断時の周期が解析の方が速い。
解析は静的変位がほぼ一致するように温度荷重を与えた。
初めは温度荷重によりケーブル張力を求め、片方のケーブルをそのまま温度荷重、もう片方を求めた張力で「あたかもあったかも」にする方法で解析を回したが、減衰がかからなかった。(DYNA_VIBRAを使用)
次に、千代岡さんから教えていただいた2段階解析をした。
2段階解析では温度荷重はできない?エラーがでてしまった。
そのため、ケーブル2本とも「あたかもあったかも」の方法を使い、片方は張力をかけたまま、もう片方を途中で張力0にして解析を回した。
この方法で減衰はかかった。(この方法を①とする。)
実験と解析の結果
| 静的 | 動的 | 健全時 | DAF | |
| 実験 | 18.34 | 34.54 | 0 | 1.884 |
| 解析 | 18.40 | 35.43 | 0 | 1.926 |
ケーブル破断時の周期が実験の方が速い。
DYNA_VIBRAを使用し、片方を温度荷重、もう片方を同じ張力で点載荷にしたとき、健全時の変位が0にならない。
つまり、温度荷重と点載荷の両方を使用するときはDYNA_VIBRAは使えない?
DYNA_NON_LINEを使用して片方温度荷重、もう片方を点載荷にした時、健全時の変位は0になった。(この方法を②とする。)
DYNA_VIBRAを使用しているときはcalc_modeとcalc_amor_modalを使用して減衰の設定をしていたが、DYNA_NON_LINEでそれらを使った減衰設定がわからなかった。
そこで材料設定の部分で減衰に関わるα、βを設定し減衰をかけた。しかし、思ったよりも減衰がかからなかった。
(この理由はケーブルのみにα、βを設定していたから)
このときの実験と解析のグラフは次のようになった。
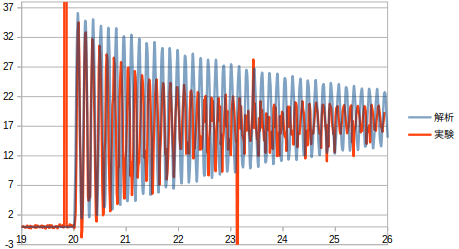
このグラフでは周期のズレは小さくなっている。このことから周期のズレはケーブルの有無によるものだと考える。
方法②を解析の途中でtime stepを変える解析してみた。(0s〜19sまでtime steo0.01、19s〜30sまでtime step0.001)
またα、βは梁のみに設定して解析を行った。
このときの実験と解析のグラフは次のようになった。
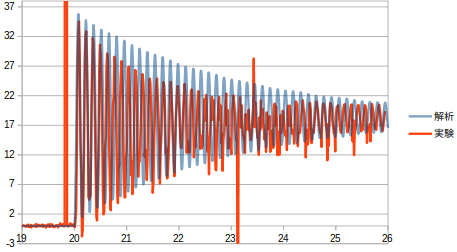
| 静的 | 動的 | 健全時 | DAF | |
| 解析 | 18.40 | 35.79 | 0 | 1.945 |
FrontlSTRチュートリアルP85〜に片持ち梁の動的変位の理論値が載っていた。(正しいとは限らない)
これによると片持ち梁のDAFの理論値は1.9753となる。
断面10mm*50mm,長さ500mmの片持ち梁モデルで動的解析を行ってDAFを確認した。
まずはステップ荷重を梁の先端に載荷する解析を行った。しかし、エラーがでてしまった。
Exception utilisateur levee mais pas interceptee. !
! Les bases sont fermees. ! ! Type de l'exception : NonConvergenceError ! ! ! ! Arrêt pour cause d'absence de convergence avec le nombre d'itérations requis ! ! dans l'algorithme non-linéaire de Newton. ! ! La base globale est sauvegardée. Elle contient les pas archivés avant ! ! l'arrêt. ! ! ! ! Conseils : ! ! - Augmentez ITER_GLOB_MAXI. ! ! - Réactualisez plus souvent la matrice tangente. ! ! - Raffinez votre discrétisation temporelle. ! ! - Essayez d'activer la gestion des événements (découpe du pas de temps par ! ! exemple) dans la commande DEFI_LIST_INST.
次に「あたかもあったかも」を用いてtimestep0.001で解析を行ったところ解析は回り、DAFは1.872となった。
理論値と考えていた1.9753にはならなかった。
| 長さ(mm) | 片持のDAF | 単純のDAF |
| 100 | 1.258 | 1.0962 |
| 200 | 1.7225 | 1.36 |
| 300 | 1.9082 | 1.6528 |
| 400 | 1.9609 | 1.8328 |
| 500 | 1.9791 | 1.9148 |
| 600 | 1.9878 | 1.9527 |
| 700 | 1.9884 | 1.9701 |
| 800 | 1.9915 | 1.9789 |
| 900 | 1.9944 | 1.9858 |
| 1000 | 1.9947 | 1.9889 |
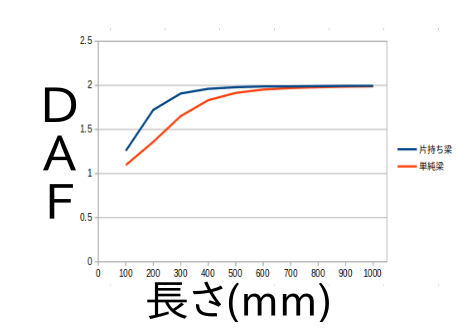
・境界条件:片持ばり
塔の長さを変えながら先端に水平方向の荷重を与えた。
塔の長さを長くすることで先端が境界条件を考えない自由な動きが出来るようになったため、DAFが2に近づいたと考える。
・境界条件:単純梁
DRYのみを自由にした単純梁モデルを作り、梁の長さを変えながら、梁中央に荷重を与えた。
片持ち梁と同様に長くすることで中央が境界条件を考えない自由な動きが出来るようになったため、DAFが2に近づいたと考える。
・両方を比べてみて
片持ち梁の方が同じ長さ時のDAFが大きく、また長さの伸びに対するDAFの上がり方が大きかった。
しかし、固定部からの距離で見る(片持ちL=100mmと単純L=200mmのように比較)と単純梁の方がDAFは大きくなっている。
この理由を考えながら、境界条件がどのようにDAFに影響するかを検討していきたい。
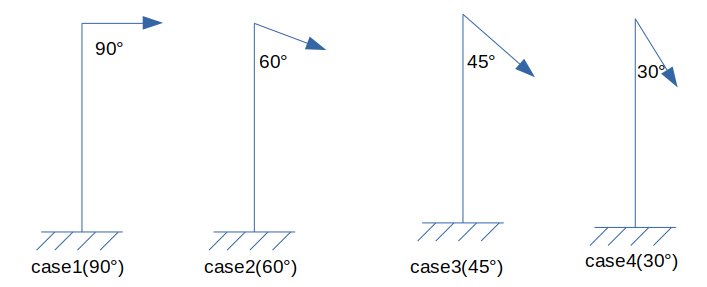
塔の長さ、荷重は同じにして、ケーブルの角度のみを変化させDAFの違いを調べた。
| case1 | case2 | case3 | case4 | |
| DAF | 1.88059 | 1.88059 | 1.88059 | 1.88059 |
この結果からケーブルの角度はDAFに影響しないことが分かった。
・2本の場合(減衰なし)
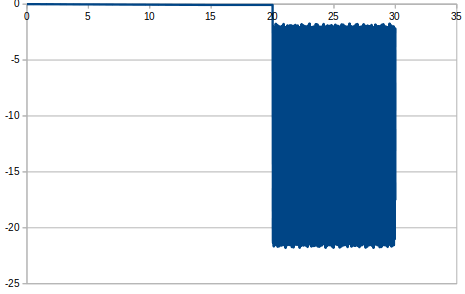
破断していないケーブルがあるため、初期位置より破断したケーブル側へ揺れることはなかった。
7月2日の実験ではタワーにケーブルを1本取り付けたものと2本取り付けたものを用意し、ケーブルを破断させたときのタワーの先端変位を測定した。
・1本の場合

1本のときは上のような状態からケーブルを切った。
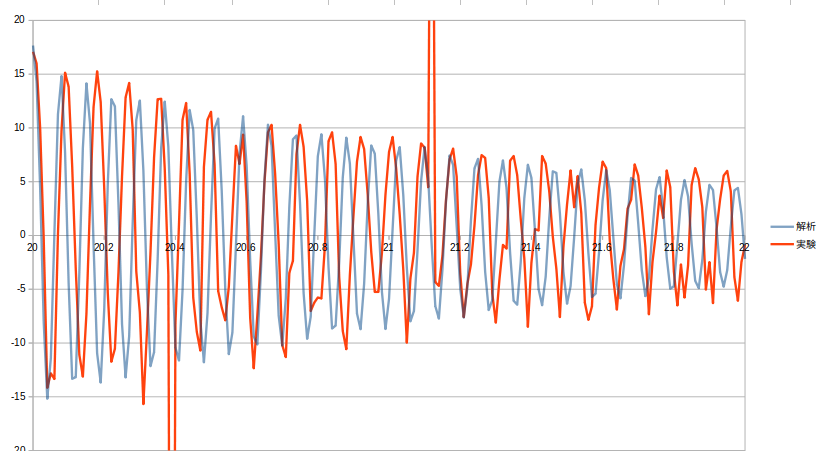
実験と解析の先端変位のグラフは次のようになり、近い値となった。
しかし、解析の方が周期が早く見える。
time stepを0.01から0.005にすることで周期の問題は解決した。(解析時間短縮のため解析時間を30sから20sへ、破断開始を20.1sから10.05sへ変更した。)
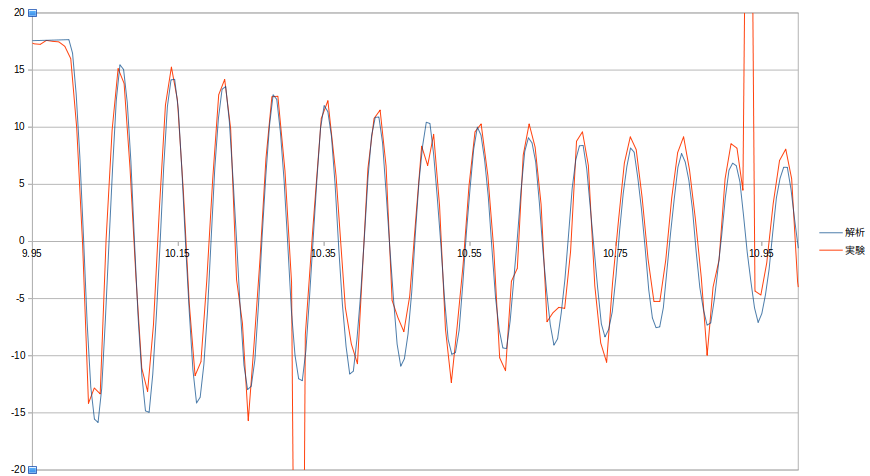
DAFは1.897となり、理論値に近づいた。
time stepを0.005から0.001にすることでDAFが1.919となりさらに理論値に近づいたが、周期の問題がまた発生した。
この原因はまだわかっていない。
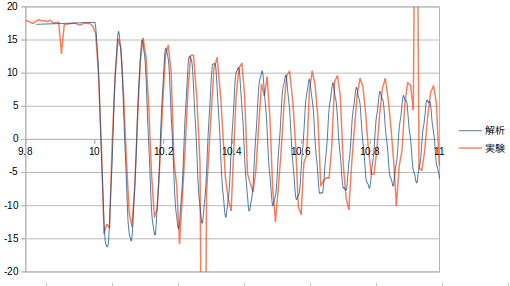
実験と解析結果
| 動的変位 | 静的変位 | DAF | DAF理論値 | ||
| 実験 | 31.76mm | 17.70mm | 1.794 | 1.963 | |
| 解析step0.01 | 32.84mm | 17.66mm | 1.859 | 1.963 | |
| 解析steo0.005 | 33.50mm | 17.66mm | 1.897 | 1.963 | |
| 解析step0.001 | 33.90mm | 17.66mm | 1.919 | 1.963 |
7月2日に行った実験の再現を解析で行っている。
ケーブル部分にプレストレスを与えるため、温度荷重のかけかたを学んだ。

温度荷重によってプレストレスが入り、塔がたわむことを確認できた。
今後はたわんだ状態からケーブルを破断させたときの挙動を確認していく。
これまでの減衰定数の計算の考え方は間違っていた。
https://wwwra.meijo-u.ac.jp/labs/ra007/murata/pdf/textbook/sindo_2005-2.pdf
このページを参考にした。
\( δ=\displaystyle \frac{Y_1}{Y_2} \)で対数減衰率δを求めるが、\( Y_1 \),\( Y_2 \)は最大変位から破断後の静的変位を引いたものである。
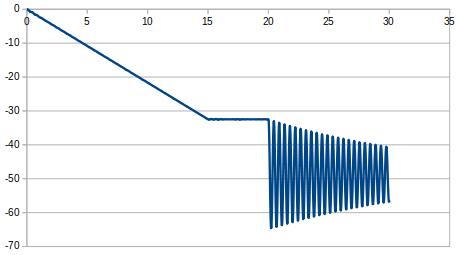
この減衰定数を計算すると0.00477と与えたかった0.005に近い値となった。
・減衰定数を0.05に設定し、解析を行った。
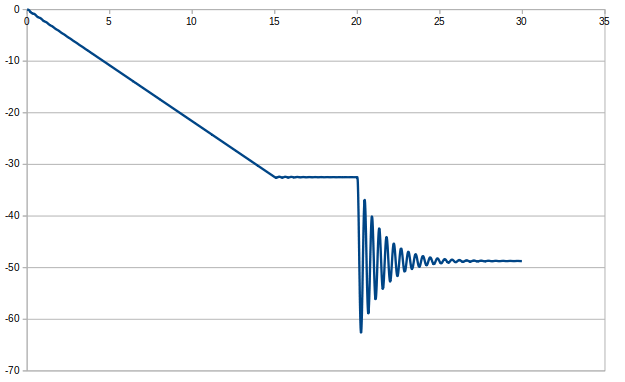
このグラフからDAFを求めると1.850で理論値のDAF=1.855に近い値となった。
・減衰定数0.1に設定した場合
理論値が1.730なのに対し、解析から求めたDAFは1.725となった。
構造関係メモから\( DAF=1-\cos\omega t \)と表すことが出来ることを理解した。
減衰についてだが、現在自分の与えたい減衰定数を反映するができていない。
減衰定数0.005で与えたいところを、変位のグラフから計算すると0.0099となっている。
| 実験値 | 解析値 | |
| 3本静的 | 32mm | 32.48mm |
| 破断時(動的) | 68mm | 65.15mm |
| 2本静的 | 47mm | 48.72mm |
健全時を原点にとり、動的変位と静的変位の比をとったものと、自然長を原点にとった時とではDAFが異なる値となった。
健全時を原点にとったものを\( DAF_{健} \)、自然長を原点にとったものを\( DAF_{自} \)とする。(\( DAF_{自} \)は\( S_{0} \)=0とする。)
構造関係メモから自然長を原点にとったDAFは\( DAF={1-\displaystyle \frac{\cos\omega t}{N}} \)と表される。これを\( DAF_{自理} \)とする。
tは破断開始から最大変位にいたるまでの時間を代入する。
解析、実験の結果は次のようになった。
| \( DAF_{健} \) | \( DAF_{自} \) | \( DAF_{理} \) | \( DAF_{自理} \) | |||
| 解析 | 2.01 | 1.337 | 2.00 | 1.333 | ||
| 実験 | 2.40 | 1.447 | 2.00 |
固有振動数を解析で求め、レイリー減衰で用いるα、βを計算し減衰をかけた。
減衰定数0.005
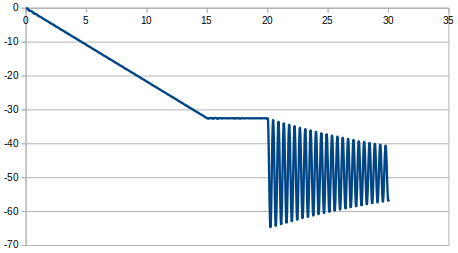
減衰定数0.005よりもかかっている気がする、、
解析方法を見直す必要あり
実験した3本モデルを減衰を考慮して解析してみた。
グラフを見ると減衰しすぎな気がする。なにか設定をミスってる可能性あり。
減衰0.5%のとき
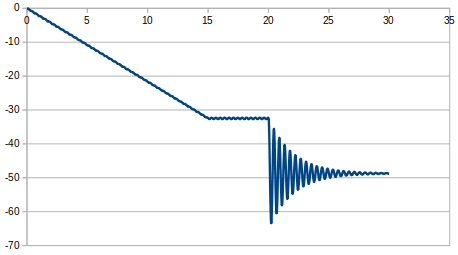
減衰1%のとき
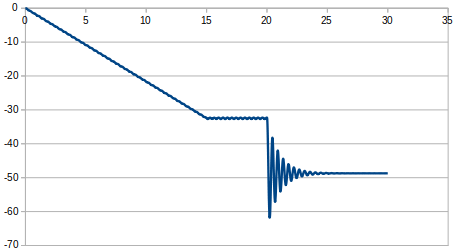
減衰5%のとき
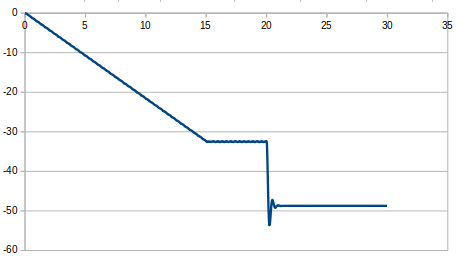
断面、縦22mm、横70mmで高いところから紐+バネで吊るした解析を行ってきた。しかし実験では縦方向の変位だけでなく、横方向にも揺れてしまった。
これを踏まえ断面、縦70mm、横22mmの縦長にし、低いところからバネのみを使用した実験を行った。結果横方向の揺れは少なくなった。
今回の実験の結果からばね定数等を求め解析を行い、実験と解析の自然長からの変位は次のようになった。
| 実験値 | 解析値 | |
| 3本静的 | 32mm | 32.48mm |
| 破断時 | 68mm | 65.15mm |
| 2本静的 | 47mm | 48.72mm |
動的変位と2本の静的変位の比から求めるDAFは次のようになった。
| 実験値 | 解析値 | |
| DAF | 1.447 | 1.337 |
今回のバネの本数が破断により3本から2本になったため、DAFの理論値は1.333である。
DAFを衝撃係数問題から求めると理論値は2になり、実際に解析でも2となった。
5月31日に実験をIHIや他大学の教授に見せ意見をいただいた。
初めの実験モデルでは複数のパラメータにより、調べたい対称が何に起因しているのかわからないのでは、という意見だった。
そこで簡単なモデルから徐々に進めていくことにした。
初めは3本のケーブルで鋼材を吊るしたモデルで、真ん中のケーブルを切ったときの挙動を見ることにした。
千代岡さんに"あたかもあったかも"を教えていただき、salomeで解析を初めた。実験はまだしていない。
3本のケーブルで真ん中の1本を破断させたときの時間と変位のグラフは次のようになった
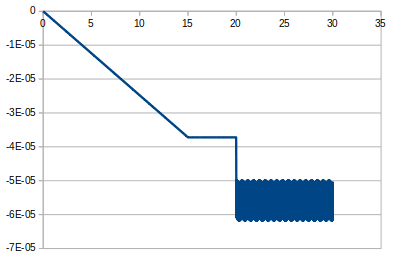
この結果に加え、ケーブルが2本のときの静的変位を調べることでDAFを求めると、DAF=1.317となった。
(DAFの導き方は千代岡さんの卒論を参考にした。)
次にケーブルの剛性を変化させることでDAFの違いを求めようと思ったが、ケーブルの剛性を変化させても変位量は変化するが変位の割合は変化しないと考えられる。
そこでケーブルの本数を増やし、ケーブルの破断する数を変化させたときのDAFを調べることにした。
ケーブルの本数を9本にして真ん中の1本を破断させたときの時間と変位のグラフは次のようになった。
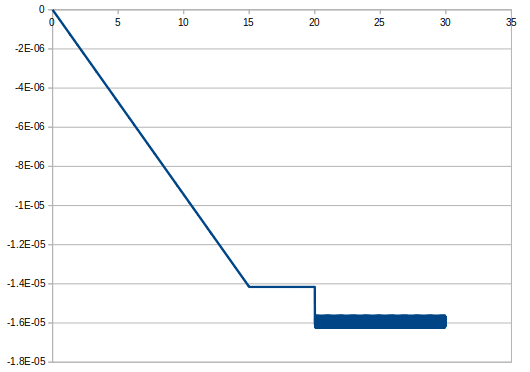
DAFは1.177となった。
今後は3本破断、5本破断、7本破断の解析を進めていく。
衝撃を与える時間を変えてみた
マルチファイバーに衝撃を与えた時の先端変位
http://opencae.gifu-nct.ac.jp/pukiwiki/index.php?plugin=attach&refer=SALOME-Meca%A4%CE%BB%C8%CD%D1%CB%A1%B2%F2%C0%E2&openfile=16-00.pdf このページを参考にして解析した
AFFE_CARA_ELEMのわからない用語を調べる必要あり
EXCENTREMENT_FO: 法線方向で、格子と平均曲面の間の距離を与える関数。法線方向に、グリッドと平均サーフェスに入る距離を定義する (モデリング DKT, DST, GRILLE_EXCENTRE).
点を固定できるのか: lineをグループ化で固定、載荷の点を作ったがAFFE_CHAR_MECAで点が出てこないため固定できない
GROUP_MAを選択していたため点が出てこなかった、GROUP_NOを選択したら点を選べるようになり固定できた
固定面をどうやってつくるのか: 長方形フェースを固定したい面に付ける方法を考えたがうまくできなかった
https://in.midasit.co.jp/wp-content/uploads/2020/07/constrcution-83-civil-book.pdf
https://in.midasit.co.jp/wp-content/uploads/2020/07/constrcution-84-civil-book.pdf
サンドイッチ梁
| メッシュの長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.7 | 155192 | 0.08378905246 | 15.365 | 安藤 |
| 0.8 | 138808 | 0.08380386491 | 15.350 | 安藤 |
| 0.9 | 82587 | 0.083707073981 | 15.45 | 兼田 |
| 1.1 | 38671 | 0.084201207602 | 14.95 | 兼田 |
| 1.2 | 31929 | 0.083688 | 15.466 | 柴田 |
| 1.3 | 28621 | 0.083669 | 15.4857 | 柴田 |
| 1.4 | 28854 | 0.08368 | 15.47 | 佐藤 |
| 1.5 | 20015 | 0.084052 | 15.10 | 佐藤 |
| 1.6 | 19448 | 0.0835402938 | 15.62 | 皆川 |
| 1.7 | 13801 | 0.0834355098 | 15.72 | 皆川 |
| 1.8 | 12528 | 0.083733 | 15.42 | 永山 |
| 1.9 | 11769 | 0.083924 | 15.23 | 永山 |
| 2 | 10699 | 0.084076876559 | 15.074 | 辻 |
| 3 | 3579 | 0.08414561753 | 15.004 | 辻 |
| 4 | 1628 | 0.082794 | 16.37 | 服部 |
| 5 | 1016 | 0.083033 | 18.89 | 服部 |
| 6 | 839 | 0.082882 | 16.26 | 梶原 |
| 7 | 554 | 0.080871 | 18.28 | 梶原 |
| 8 | 285 | 0.079995 | 19.20 | 工藤 |
| 9 | 261 | 0.078980 | 20.22 | 工藤 |
| 10 | 232 | 0.081911 | 17.26 | 佐々木 |
| 11 | 208 | 0.075676 | 23.56 | 佐々木 |
異方性一次 [#p29b4460]
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.7 | 144563 | 0.505252 | 2.76 | 安藤 |
| 0.8 | 141517 | 0.504692 | 2.64 | 安藤 |
| 0.9 | 91648 | 0.502595 | 2.216 | 兼田 |
| 1.1 | 27160 | 0.489914 | 0.363 | 兼田 |
| 1.2 | 24675 | 0.487088 | 0.791 | 柴田 |
| 1.3 | 23446 | 0.4868010 | 0.995 | 柴田 |
| 1.4 | 17738 | 0.485999 | 1.16 | 佐藤 |
| 1.5 | 15438 | 0.485180 | 1.33 | 佐藤 |
| 1.6 | 15900 | 0.483286 | 1.71 | 皆川 |
| 1.7 | 12142 | 0.477952 | 2.80 | 皆川 |
| 1.8 | 11604 | 0.482085 | 1.9554 | 永山 |
| 1.9 | 10391 | 0.470887 | 4.2329 | 永山 |
| 2 | 10291 | 0.480910 | 2.19 | 辻 |
| 3 | 2328 | 0.431937 | 12.15 | 辻 |
| 4 | 1500 | 0.430156 | 12.52 | 服部 |
| 5 | 432 | 0.282968 | 42.45 | 服部 |
| 6 | 356 | 0.3441556 | 30.00 | 梶原 |
| 7 | 196 | 0.213934 | 56.49 | 梶原 |
| 8 | 104 | 0.229874 | 53.25 | 工藤 |
| 9 | 81 | 0.232308 | 52.75 | 工藤 |
| 10 | 78 | 0.203271 | 58.65 | 佐々木 |
| 11 | 63 | 0.222316 | 54.78 | 佐々木 |
等方性二次 [#vb0def3f]
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.7 | 144563 | 0.430124 | 3.22 | 安藤 |
| 0.8 | 141517 | 0.430132 | 3.22 | 安藤 |
| 0.9 | 91648 | 0.430020 | 3.197 | 兼田 |
| 1.1 | 27160 | 0.429828 | 3.151 | 兼田 |
| 1.2 | 24675 | 0.429836 | 3.15 | 柴田 |
| 1.3 | 23446 | 0.42974 | 3.13 | 柴田 |
| 1.4 | 17738 | 0.429797 | 1.3 | 佐藤 |
| 1.5 | 15438 | 0.429958 | 3.14 | 佐藤 |
| 1.6 | 15900 | 0.429755 | 3.18 | 皆川 |
| 1.7 | 12142 | 0.429676 | 3.11 | 皆川 |
| 1.8 | 11604 | 0.429829 | 3.1507 | 永山 |
| 1.9 | 10391 | 0.429684 | 3.1159 | 永山 |
| 2 | 10291 | 0.429620 | 3.10 | 辻 |
| 3 | 2328 | 0.429169 | 2.99 | 辻 |
| 4 | 1500 | 0.429254 | 3.01 | 服部 |
| 5 | 432 | 0.428170 | 2.75 | 服部 |
| 6 | 356 | 0.428452 | 2.82 | 梶原 |
| 7 | 196 | 0.42591 | 2.21 | 梶原 |
| 8 | 104 | 0.426074 | 2.25 | 工藤 |
| 9 | 81 | 0.425552 | 2.12 | 工藤 |
| 10 | 78 | 0.488382 | 17.20 | 佐々木 |
| 11 | 63 | 0.423972 | 9.0534 | 佐々木 |
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.7 | 1455234 | 0.422484 | 0.01388 | 安藤 |
| 0.8 | 142973 | 0.422570 | 0.01409 | 安藤 |
| 0.9 | 91648 | 0.420437 | 0.897 | 兼田 |
| 1.1 | 27160 | 0.405618 | 2.659 | 兼田 |
| 1.2 | 24675 | 0.404349 | 2.96 | 柴田 |
| 1.3 | 23446 | 0.404185 | 3.00 | 柴田 |
| 1.4 | 17738 | 0.398604 | 4.34 | 佐藤 |
| 1.5 | 15438 | 0.396593 | 4.83 | 佐藤 |
| 1.6 | 16122 | 0.398212 | 4.44 | 皆川 |
| 1.7 | 12026 | 0.393411 | 5.59 | 皆川 |
| 1.8 | 11604 | 0.393668 | 5.53 | 永山 |
| 1.9 | 10391 | 0.390695 | 6.24 | 永山 |
| 2 | 10921 | 0.395103 | 5.18 | 辻 |
| 3 | 2328 | 0.324762 | 22.06 | 辻 |
| 4 | 1500 | 0.155013 | 62.80 | 服部 |
| 5 | 432 | 0.065278 | 84.33 | 服部 |
| 6 | 357 | 0.213062 | 48.87 | 梶原 |
| 7 | 196 | 0.1019 | 75.55 | 梶原 |
| 8 | 104 | 0.1158624 | 72.20 | 工藤 |
| 9 | 81 | 0.1255118 | 69.88 | 工藤 |
| 10 | 78 | 0.07733 | 81.44 | 佐々木 |
| 11 | 63 | 0.1999 | 52.03 | 佐々木 |
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.7 | 198464 | 6.54281 | 1.91 | 安藤 |
| 0.8 | 113812 | 6.5104 | 2.39 | 安藤 |
| 0.9 | 40280 | 6.3631525 | 4.60 | 兼田 |
| 1.1 | 30055 | 6.3363525 | 5.00 | 兼田 |
| 1.2 | 26467 | 6.3043375 | 5.48 | 柴田 |
| 1.3 | 25180 | 6.304355 | 5.48 | 柴田 |
| 1.4 | 32212 | 6.31612 | 5.31 | 佐藤 |
| 1.5 | 17753 | 6.1209 | 8.23 | 佐藤 |
| 1.6 | 14296 | 6.2044625 | 6.98 | 皆川 |
| 1.7 | 13596 | 6.2156625 | 6.81 | 皆川 |
| 1.8 | 2866 | 5.737755 | 13.98 | 永山 |
| 1.9 | 6001 | 5.7263625 | 14.15 | 永山 |
| 2 | 5617 | 5.6458525 | 15.355 | 辻 |
| 3 | 2309 | 5.4728755 | 17.948 | 辻 |
| 4 | 617 | 3.6160575 | 0.458 | 服部 |
| 5 | 494 | 3.8580375 | 0.422 | 服部 |
| 6 | 581 | 2.50682 | 62.416 | 梶原 |
| 7 | 133 | 1.41225 | 78.827 | 梶原 |
| 8 | 78 | 1.2887175 | 80.68 | 工藤 |
| 9 | 72 | 1.2879925 | 80.69 | 工藤 |
| 10 | 60 | 1.14344 | 82.85 | 佐々木 |
| 11 | 65 | 1.23124 | 81.154 | 佐々木 |
コマンドを学んだ。
pwd:今いる場所
ls:今いる場所のフォルダ名ファイル名等を見る
mkdir:フォルダの作成
cd:ファイル間の移動(ディレクトリーの移動)
gedeit ファイル名 .tex & :テキストファイルを開く
vi:ファイルを開く
Esc : q:開いたファイルを閉じる
cp 元のファイル名 新しいファイル名:元のファイルをコピー
cat:ファイルの中を確認
rm:ファイルの削除、cd .. :1個前に戻る
rmdir:フォルダを削除