![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
2024年4月からは千代岡の修論日誌に研究成果等を記載します。
3月までに書いたことはそのままこのページに残しておきますが、大事なことはこちらにまとめます。
研究内容:様々な外力が作用する斜張橋の動的応答解析
model300のケーブル7本モデルのC1破断時の主桁中央の鉛直変位を減衰率を変えて求めた.
減衰率の設定法は秋山さんの修論日誌に書かれているレイリー減衰の与え方を参考にして行った.(全ての部材に減衰を与えている.)
・減衰0%
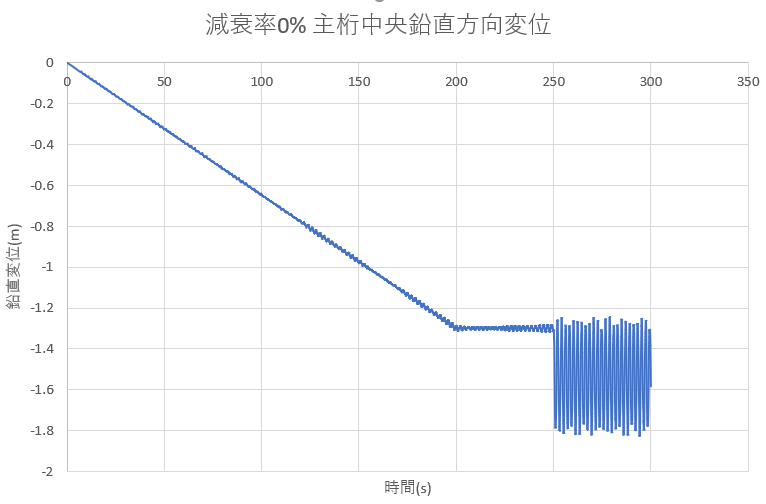
基本的に減衰率の値以外の設定条件は先輩方が設定したものと同じである.
減衰率5,10%だと主桁中央変位の最もたわむ値が変わっているが,これはtimestepの切り方が悪いからだと思われる.
ステップ条件を複数条件→荷重時間に対する初期比率を0.01にやっているからかな?(一応、一定条件でtimestepを切る方法はあるが,これを使っていないのは収束しなかったために解析が回らないことをできるだけ減らすためだったはず.)
先生に結果をお見せしたところ,問題なさそうとおっしゃていたのでとりあえずはこれでいいと思う.(やらかしてたらすぐにやり直そう...)
R3年度バックアップの根本さんのお名前が書いてある外付けHDDの内部にchiyooka→soturon→Salomesoturonに入っています.
ファイル名のDは死荷重,Cは集中荷重を示しています.また,どのファイルにも最低限commファイルとmedファイルは入っていますので,解析を回すこと自体はできるようになっています.
自分の研究成果の課題点(院でやること)をまとめておく。
・実験的検討を行う。解析結果とSalome_Mecaで出したデータを比較.(Marcのほうでも出しておいたほうがいいかな?)
・橋モデルをSalome_Mecaで作成して,今回得られた結果とどう変わってくるか検討.まず,Salomeでも解析できる状態に持っていくことからスタートだけど...。
研究室で編み出した連鎖崩壊のメソッドの妥当性を確認する。これまで連鎖崩壊に関する解析を様々な先輩が行なっていた(行なっている)が、その中でDAFを用いた連鎖崩壊に関するメソッドを編み出した。
しかし、その妥当性の評価を行なっていなかったので、その評価をSalome-mecaで簡単なモデル(以降、簡易モデルと表記)を作成して行なってみる。
Salome-mecaで行う理由としては...
①ビーム要素を用いた動的応答解析の手法ができていないのでそれをできるようにしたい。研究室にはSalome-MecaとMarcの2種類の解析ソフトがあるが、現状そういった解析ができるのはMarcだけ。
②2種類以上の解析ソフトで解析できるようにした上で、同じような結果が得られれば解析結果の信頼性が増す。
卒論としての目標は、簡易モデルでのDAFを用いた連鎖崩壊に関するメソッドの妥当性評価を行う(余裕があれば、モデル長を変えてみるのもあり? 例:1m⇒10m)
DAFとは?
動的増幅率を表す指標。式等はこちらを参照。
3/22 卒業式
3/23 一旦実家に帰省
4月以降については修論日誌に書く。
大学卒業までにやること
まずは東北支部の発表に備える!
・本論作成(3/15まで)
・引継ぎ関連(先輩方にお願いしないと...)
・以前、Salomeで作成した橋モデル作成の続き
・wiki整理
・謝恩会準備(研究とは関係ないが...)
卒論まで残り1週間 残りの期間でやること
・2回目練習の動画を見て,反省会(メモしきれなかったところもあるため...)
・スライドの修正
・概要は卒論用に手直ししたので、一度指導教員にお見せする
・ひたすら練習.個人練習を含め,15回くらいはやりたい
2024年 1,2月にやること
・0.01sから短めにtimestepを切ると途中で張力が落ちる問題を解決する。
・東北支部、卒論に向けての概要とスライド作成
・(研究とは関係ないけど...)謝恩会の準備
ラストスパート!!自分のできる限りのことは尽くす!
2023年 12月にやること
・簡易モデルで得られる張力の値がMarcと大きく異なる謎を解明する。何とか来週中(12月の2週目)までに解決策を見つけたい。
・橋モデル:model300をsalomeで作成する。(橋はすでにgeometryで作成し、複雑な桁断面の作成方法も分かったので、後は断面作成しmeshを切るだけ。)
・PRE_EPSIを使ったモーダル解析(山本君と共同研究)
・12/22に向けての中間発表の準備
今年もいよいよ今月で終わり、これまでの成果を自信を持って発表できるようにしたいな。
2023年 11月にやること
・動的解析(線形&弾塑性を含んだver.)でプレストレスを考慮した解析をできるようにする。
・model300をsalomeで作成する。
・PRE_EPSIの解析手法の検討(山本君と共同研究)
・ビーム張力を見れるようにする。
2023年 10月にやること
・簡易モデルの弾塑性周辺の設定見直し→ケーブルには何も設定しないで解析してみる
・ピン接合の設定確認(ばねが本当に一軸方向のみに作用しているか。)
・簡易モデルにプレストレス入れてみる
・張力だけを落として集中荷重のみが載荷し続ける挙動再現(片持ち梁で)
・Salome-mecaの簡易モデルを用いた動的応答解析のやり方を学ぶ
・Salome知識(ソリッド絡みの知識)復習 10月に来る3年にSalomeの使い方を教えるため
2023年夏休みにやること
8月は実家に戻るまではピン接合問題(Salome,calculixの両方の解析ツールから)について考える。
Salomeを使えるノートパソコンを借りることができたので、実家に戻ったら,Salomeに関する資料を読みつつ解析する。(calculixのほうも考えてみる。後、ノートパソコンは自分のものではないので、丁寧に扱うこと!何かあったら、報告するように!)
何か進捗があれば、先生に報告することを忘れないように。
秋田に戻ったら、中間発表に向けて今まで以上に気合を入れて取り組むこと!
2023年7月にやること
(1)Salome-Mecaでビーム要素の弾塑性解析をできるようにし、引張もしくは圧縮のみのグラフを導出できるようにする。
⇒ケーブルには引張しか存在しないので、それを再現するため。
(2)Salome-Mecaでピン接合をできるように考え、Marcの簡易モデルで導出した先端変位のグラフをSalome-Mecaでも導出できるようにする。(違う解析ソフトでも計算手法が同じなら、結果も同じものがでるはず。)
今は上記2つを重点的に行う。今のままだと、10月の中間発表で発表することがない状況に...。
(3)英語ゼミの中間発表に向けてスライド作り
⇒これは研究背景と今取り組んでいることとこれからどうしていきたいか話すと思われる。(大学院入試で研究について話すことをスライドを用いて説明するイメージでいいのかな?)
後は、自分にとって必要だと思う力(コミュニケーション能力とか)を鍛えること(意識して過ごすこと)や知識(英語とか土木知識)の勉強も忘れずに。
焦ってもしょうがないが、自分のやっていることなどを人に分かりやすく説明できるようには早くなりたい。
2023年6月にやること
(1)Salome-Mecaでビーム要素の弾塑性解析をできるようにする。
(2)Salome-Mecaでソリッド要素の弾塑性解析のグラフ改善(Marcに近いグラフを出したい)
(3)Salome-Mecaでピン接合をできるように考える。
(4)振動解析の勉強(動画のモデルの実際に作る)
後は、来月に大学院入試があるので、それに向けて準備する。
2023年5月にやること
(1)先月同様、salomeでの振動解析について学ぶため、code_asterの動画を視聴する。急いで取り組む必要はないみたいなので、じっくりやっていきたいと思います。(動画の視聴とその解析はさすがに今月中までに終わらせます。動画に至っては残り3つ見れば終わりなので...。)勉強してまとめたノートを共有してほしい?みたいなので、それも載せる。
(2)Marcで弾塑性解析(モデルは10×10×100mm)を行い、235MPaで降伏するか確かめる。
Salome-MecaとMarcの結果比較をするために、Salomeで梁要素,Marcでソリッド要素でモデルを作成し、弾塑性解析を行う。(wikiで調べたところ、Salomeを用いた梁要素の弾塑性解析がこれまで上手くいってなさそう?)
(3)Salome-Mecaでピン接合をできるように考える。
後は、時間があるときに院試に向けて勉強や本などを読んで知識をつける。
2023年4月にやること
(1)code_asterの動画https://www.youtube.com/@DigvijayPatankar/playlistsを視聴する。研究に取り組む前にsalomeの知識が足りないため、まずはsalomeの勉強! (字幕は英語のほうがよい。...が、話している人の声が小さいせいなのかyoutubeの問題か分からないが、おかしな英語字幕となるので、あくまで参考程度にして自分の耳で英語を聞き、参考資料も使いながら理解しつつ取り組んでみる!)
目標はGW明けに終わらせる!(どんなに時間がかかっても5月中に!)
参考資料
(2)時間があるときにMarcの使い方に慣れておく。
12/12 温度考慮した動的解析ができるようになったこととケーブルから得られた応力の話
12/6 現状の問題点と打開策を話す。
11/29 軸力絡みの話
11/22 ビーム軸力の話
11/15 特になし
11/8 PRE_EPSIを使ったプレストレス再現のお話
11/1 線形での動的解析の設定の仕方は分かった。(FORC,REACの力の導出も見れるようにした。) ただ、プレストレスは考慮してくれない。
10/25 線形解析ではプレストレスが導入できたこと、動的解析の使い方の勉強をする
10/18 プレストレス導入の話
10/11 プレストレスとピン接合絡みの話
10/4 後期1回目のゼミ 報告することは特になし
現時点で分かっている問題点と分かったこと
(以上、秋山さんの修論日誌より引用)
↑簡易モデル
↑桁断面
簡易モデルを作成して、梁の先端変位を簡易モデルのケーブル破断前と破断後のグラフを作成した。
ケーブルはピン接合、梁は原点を完全固定、ケーブルとの節点はピン接合をした。
桁の長さは1000mm,完全固定から図の上のピン接合までの距離は1000mm,梁断面は薄肉断面の幅50mm,厚さ10mm,穴あきまでの距離は2mm(空白部分の厚さは6mm)で、ケーブル断面は直径8mmある。
材料特性は以下に示す。
| ヤング率(GPa) | ポアソン比 | 密度(ton/mm^3) | |
| 梁 | 200 | 0.3 | 7.9e-9 |
| ケーブル | 195 | 0.3 | 7.9e-9 |
ケーブルに掛けたプレストレスは-100℃,熱膨張係数は1.25e-5
↑ケーブル破断前の先端変位グラフ
↑ケーブル破断後の先端変位グラフ
↑ケーブル破断後の先端変位グラフ拡大図
先端変位の理論値(片持ち梁のたわみ式から)を導出すると、15.46mmだった。破断後の最大変位(ケーブルが安定しているところを0基準とした。)は-y方向に22.5mmであり、理論値より1.45倍大きい値となった。
破断後の最大変位が理論値の1.5〜2倍程度になればいいみたいなので、これらのグラフをSalome-mecaでも導出できるのか取り組んでいく。
ちなみに、ケーブル破断後に振動したグラフができたのは、梁がケーブルによってy方向に引っ張られて、ケーブルが切れた衝撃で上下に振動したため。
↑ビーム要素で作成し、モデルの向きも合わせた。 また、メッシュの切り方も同じにした。(桁50分割 ケーブル2分割)
↑梁断面(Marcと同じ) 写真には載せてないが、ケーブル断面も作成した。(断面を作成したのは、DEFI_GEOM_FIBREで使用するため。)
モデルの作り方は桁とケーブルのモデルを作成し、メッシュを別々に切ってからコンパウンドした。
・動的応答解析は?
簡易モデルではDYNA_LINE,DYNA_NON_LINEを使って解析する。(直接積分法というもの)
・弾塑性解析は?
再現できた。しかし、降伏応力より大きめの値を設定すると収束しないエラーが出るので、反復回数やstep数の調整が必要である。
・プレストレスは?
線形静的解析の場合、温度からでも導入できる。しかし、弾塑性解析といった材料非線形の場合や動的解析だと温度を考慮してくれないので、その方法は不可。代わりにPRE_EPSIを使って再現することができる。
・途中で張力を落とす(0にする)やり方
ケーブル破断した際、張力は0になるので、それを再現するためにはDEFI_FONCTIONを使用する。それに加え、動的解析の設定を行う必要がある。(詳細は後述)
ケーブル破断後の挙動を再現するためにある時間でケーブルの張力を0に落とし、荷重をそのまま維持させる必要がある。
本来、まず簡易モデルに荷重をかけて、そのときのケーブル張力をデータから抽出して、それを張力として作用させる必要がある。
そこで、試しに片持ち梁(10✕10✕1000mm)を作成してやってみた。
梁の先端に0.1mmのバネ要素の線をつけて、バネの先端(1000,0.1,0)に適当な張力の値Ty=11700Nをかけ,集中荷重を(990,0,0)にFy=-23400Nを50sまで載荷し,70sまで安定させてから張力を落とす(0にする)ような挙動を再現しようと試みた。(70.1sでT=0に設定)
やり方として、DEFI_FONCTION(関数の定義)でNOM_PARA[INST]に設定して、VALEで数値入力する。下図はVALEの画面。表の左側が横軸,右側が縦軸に対応する。
表の左側にNOM_PARAで定義した数値(今回はINST)を入れ、表の右側(Function)に荷重の変化率(例えば、1を入力すると設定した荷重の1倍掛かることになる。)、
図は張力の設定だが、INST0のとき、0倍の荷重が載荷、INST50のとき、1倍の荷重がかかるようにして、その状態を70sまで続けるように設定した。その後、70.1sで荷重を載荷させないようにして、その状態を100sまで続けるようにした。
次にDEFI_LIST_REEL(データ定義)での設定を行う。
DEBUTは0にする。これは解析を始めるスタート地点(初期値)であり、今回INSTの0から解析を始めたいので、0を入力した。
INTERVALLEはuntil(JUSQU_Aと同じ意味。横軸の最終値)に100,PASを0.1,Interval typeをstep lengthに設定した。これで、100sを1000分割(0.1s刻み)した解析ができるようになる。
ちなみに、分割数は(until - DEBUT)/PAS で求められる。
これらの設定を踏まえた上で以下のような結果が得られた。
10/25 動的解析に直し、集中荷重を100N,張力を50Nに直した結果
70s後に梁の先端が揺れる挙動ができた!
ただ、変位だけは出せるが、何故か力を導出する設定をすると、エラーが出てしまう...。
プログラムミスということは、どこか設定がおかしいとは思うけど...?
集中荷重と張力の状態を見る限り、載荷の仕方は求めたいものが得られた。
しかし、張力が0になると、その衝撃で梁が上に持ち上がり、上下に揺れる状態になるらしいが、梁がそのままたわみ続ける挙動となった。(本来であれば、70s後に先端変位のグラフが上下に行き来するような変化になるはず。)
原因を探ってみたところ、載荷再現は問題なかったが、動的解析の設定をしていないことが原因だった。
静的解析だと、時間を考慮しない解析になり、時間に依存する荷重をかけた際のモデルの様子を見ることができないので、ケーブルが切れた際の衝撃を再現できていないから上図の挙動が得られたと思われる。
また、挙動を見る限り、荷重を掛けすぎていると思うので、荷重を減らした状態で動的解析の設定に変えて再度やってみる。
ピン接合とは?
→節点(部材と支点の節点)が自由に回転するように接合する方法。曲げモーメントが0となる。
バネ要素を用いた線で再現できる。(AFFE_MODELEのDIS_TR,AFFE_CARA_ELEMのDISCRET:K_TR_D_L)
部材と部材の距離はできる限り短くすること。(下の写真のモデルのバネ要素の線は0.1mmにしている。)
VALE[0],[1],[2]は変位に対する剛性(0,1,2の順にx,y,z方向を示す.),
[3],[4],[5]は回転に対する剛性(3,4,5の順にDRX,DRY,DRZを示す.)
回転が自由にできるピン接合を再現するなら、回転に対する剛性を緩め、変位に対する剛性を高めればよい。
REPEREはGLOBALでよい。
バネ要素を用いたピン接合は、本来節点を共有して接合するのを線を使って再現したので、できるかぎり変形は避ける必要があると思うので変位に対する剛性を高めた。(バネ要素の線自体がケーブルと桁を接続する共有節点になっているということ。)
・ばねが一軸方向に作用しているかの確認
以下の3枚の画像には桁の先端に荷重Fy=-500N掛けている。白色が元の状態,色付きが変形後の状態。
↑x方向変位に対する剛性のみを緩めた場合
y軸負の向きに力を掛けることで、ケーブルとバネ要素の線の共有節点が半時計回りに倒れ始めたときにバネが伸び、時間が経つと上の画像のようになる。
変化前と後の座標
桁側の共有節点(1000,0,0)→(1000,-14.5803,0.000175109)
ケーブル側の共有節点(1000,0.1,0)→(985.425,-14.4802,0.000175109)
↑y方向変位に対する剛性のみを緩めた場合
y軸負の向きに力を掛けることによって、バネ要素の線が伸びた状態になる。
変化前と後の座標
桁側の共有節点(1000,0,0)→(1000,-14.5802,0.000175108)
ケーブル側の共有節点(1000,0.1,0)→(1000,0.0953226,0.000175108)
↑z方向変位に対する剛性のみを緩めた場合
z軸には影響がほとんど見られなかったため、ほぼ変形せず。(モデル自体xy平面で作成しているため)
変化前と後の座標
桁側の共有節点(1000,0,0)→(999.989,-0.16365,1.965e-6)
ケーブル側の共有節点(1000,0.1,0)→(999.984,-0.0587042,1.96543e-6)
y方向変位に対する剛性を緩めた画像を見れば分かりやすいと思うが、剛性を緩めた方向にバネが真っ直ぐ伸びていることが分かる。
画像を見るかぎりは一軸方向に作用していることが分かる(バネ要素として再現はできている。)し、剛性を高めることで値を高く設定した軸方向に作用することはないと言えるのでは。
・PRE_EPSIを使ったプレストレス再現(線形静的解析 MECA_STATICS以外を用いる場合はこちらで)
AFFE_CHAR_MECA → PRE_EPSI を使ってプレストレスを再現してみた。
PRE_EPSIは変形の負荷を与えるコマンドで、説明書を見るとεと書いてあるのでひずみを与えて変形させるみたい。
PRE_EPSIの詳しい説明はこちら
今回、ケーブルにプレストレスを適用したいので、EPX(梁のローカル軸に応じた伸びの要素別定数値)を-0.00125に設定した。(この値はMarcの温度応力-100℃に相当する。後述するが、この値で桁の先端変位を見たら、Marcで得た先端変位の結果とほぼ同じだった。)
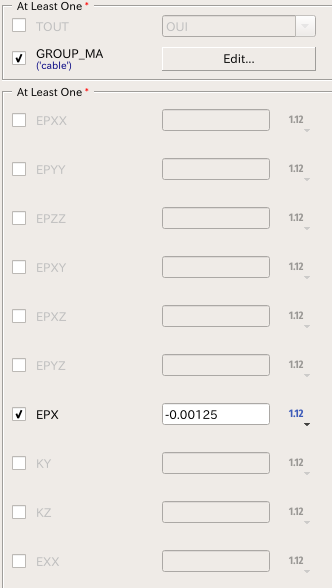
上記の設定に変えて、解析を行なったら以下の結果が得られた。
↑scalefactor1倍だと変化が見にくかったので、30倍で見てみた。
↑桁の先端変位
Marcで得た先端変位:2.49607mm
Salomeで得た先端変位:2.49608mm
Marcだと節点に温度応力-100℃与えてプレストレス再現していたので、とりあえずそれに相当するEPX(梁のローカル軸に応じた伸びの要素別定数値)を与えた。
変形図と先端変位のグラフを見る限り、再現性は高いと思うので、この方法はどうだろうか。
注意点として、何回か解析を回していると、計算自体は回るが結果が出力されないエラーが出るので、適度にRuncaseは消すこと。(今使ってる簡易モデルだと、3,4回程度までは消さずに解析可。)
・温度で再現する際の問題点
12/12追記
CREA_CHAMPとCREA_RESUを使うことで動的解析でも温度を考慮することができた。
CREA_CHAMPやAFFE_VARCの設定は一切変えずにSTAT_NON_LINEを始めとした弾塑性解析用の設定や動的解析用の設定に変えると、プレストレスが導入されていない解析になる。
線形静力学を計算してくれる(MECA_STATICS)は、材料の機械的特性は温度に依存するので勝手に計算してくれるが、それ以外の解析では材料に温度を考慮してくれないので、プレストレスは無視されるとのこと。
説明書やSalome-Mecaの掲示板なども見て、試せるものは全てやってみたが、結果は変わらずだった。(掲示板を見ると、プレストレスを考慮した動的解析はできないのかといくつか挙がっていたが、途中でやり取りが終わっていたり、誰も答えてくれないものばかりだった...。)
・やり方
CREA_CHAMPとAFFE_VARCを用いて再現可能。
過去の先輩方が行なっていた設定を参考にしながらやってみた。
線形解析で桁に死荷重Fy=-0.0183456N/mmを掛けているが、桁が上に持ち上がる挙動が得られた。
(白線が変形前、色付きが変形後)
Marcでも線形解析でのプレストレスを導入した簡易モデルのデータがあったので、比較してみたところ以下の結果が得られた。
| Marc | Salome | |
| 桁の先端変位(mm) | 2.4954 | 2.49607 |
SalomeでもMarcとほぼ同じ結果が得られたのでプレストレスの導入はできていると判断してよいだろう。
後、ピン接合の箇所を確認したところ、変形は見られなかった。
軸力はEFGE_ELNOの[N]で見る事ができることが分かった。Nは法線方向の力を意味している。(Marcだとbeam axial forceで軸力を見ることができ、その値とほぼ一致したので恐らくこれであっていると思われる。)
見る方法だが、medファイルをParaViSで閲覧し、フィルター→mechanic→ELNOfieldToSurfaceを選択すればOK。
参考資料
↑Salomeで出力される力やひずみなどについて詳しく書かれている。
模索中のメモ>
節点力から求める軸力はあまりにも値が大きすぎることから、ケーブルを要素分割して、ピン固定側(0,1000,0)の要素にPRE_EPSIを掛けてケーブルを引張り、ケーブル内の応力を求めて軸力を出してみた。
しかし、得られた軸力は4Nほどでケーブル破断後のモデルにその力を掛けてみても、死荷重-0.01848N/mmのほうが大きく桁が持ち上がらなかった...。
PRE_EPSIを使って力を見てみる人が質問していたので見てみたが、自分と同じような問題に悩ませていたようだった。(内容を要約すると、この人は変位と反力は合ってるのに、求めたい力が正しく導出されなくて困っている。)
ただ、回答していた人があるテストケースの存在を教えてくれて、それを閲覧したところDEFI_MATERIAUのPOST_ROCHEというコマンドを使えば解決できる可能性があることが分かったので、それを試してみる。
12/12追記:残念ながら自分の使っているSalomeのversionではそのコマンドが存在しなかった...。
timestepを0.01より小さな値で刻むと安定状態に入る直前に張力が落ちてしまう問題が生じてしまう。
↑初期モデルから得た張力(timestepを0.01にしている) 要素分割をしたときの張力も取ってみたが、上のグラフと同じ結果が得られた。
↑99sと100sの間の様子 一瞬だけ張力が落ちているのが分かる。
原因としては温度を用いたプレストレスが問題であることが分かった。一旦温度を用いるのはやめて、以前行なっていたひずみを与えてプレストレスを再現するPRE_EPSIで改めて解析してみた。
ただ、PRE_EPSIは設定したひずみになるような外力を与えているので、適用した要素(ケーブル)には与えたひずみをもとに応力や外力を計算してしまうため、ケーブルにそのまま適用することはできない。
そこで、ケーブルを10要素に分割して、1要素((0,1000,0)側)にPRE_EPSIを適用してプレストレスを再現した。
↑白色のところにPRE_EPSIを適用した。
↑変位も張力も温度で解析していたときとほぼ一致しつつ、張力が落ちてしまう問題も回避できたのでこれで進めてみる。
↑ただ、個人的に気になる点として、0.1Nほどの振れ幅が見られる。これって、無視できるものとして考えていいのだろうか...。
(追記)無視していいそうです。
1m(1000mm)の桁長で解析を行なったが、思っていた以上の衝撃力が出なかった。
そこで、桁長を10m(10000mm)に変えて解析を行なってみた。(断面の形状や境界条件等は変えていない。)
・問題点
↑1m簡易モデルの初期モデルは上記のような挙動が得られていた。
しかし、10m簡易モデルでは下にたわんでしまった。(120sの様子)
↑ケーブル1本モデル
↑ケーブル2本モデル
この状態でケーブル1本モデルの解析を行なってみたところ、以下の結果が得られた。
ただ、ケーブル2本モデルで解析を行うと,初期モデルのC1ケーブルに圧縮が発生することが確認できた。(→C2のプレストレスを落とす。)
対策>
桁がたわむのは問題ないらしい。まず、1本モデルの結果をまとめる。
2本モデルに関しては、C2のプレストレスを落として再解析。
このモデルは初期モデルで得た初期張力を桁の先端に元々ケーブルがあったかのように掛け、100sまで死荷重と見せかけの張力を載荷し、20s安定させてから張力を0にする(ケーブル破断を再現)。Tstはある時間の張力を表している。
2024年のデータ
12/20
120s後、10s,5s,1s,0.1s,0.05sの時間を掛けて張力を0に落とし、そのときの衝撃力を見た。その様子を縦軸を変位,桁の上フランジの応力,下フランジの応力、横軸を時間のグラフを作成した。(115s~135s区間を載せた。)
↑Salomeの結果
↑Marcの結果
10s〜0.1sまではよさそうな結果が得られているが...0.05sを見ると大きく揺れ過ぎな気がする。それに、Salomeのほうは張力を0に落とす前に振動しているし...。
・問題点
本来であれば、0.01sとも比較するつもりだったが、初期モデルから張力を取る際に99s〜100sの間で張力が落ちてしまっている。
そのため、そのデータをケーブル要素なしモデルに入れても安定させる時間(100s〜120s)で振動してしまっている。
↑初期モデルから得た張力(timestepを0.01にしている) 要素分割をしたときの張力も取ってみたが、上のグラフと同じ結果が得られた。
↑99sと100sの間の様子 一瞬だけ張力が落ちているのが分かる。
↑得た張力をケーブル要素なしモデルにあてはめた変位
ちなみに、0.005sの場合
50sで下がって、100sで上がっている。これ...何が起こっているんだ?
また、0.05s以降から衝撃力が出過ぎな気がするけど...これはこれでいいのだろうか。
上フランジ応力
模索中に得られた結果>
12/13
PRE_EPSI、もしくは温度を用いた場合でもケーブル内の応力は約0.085MPaとほぼ一様に出力されており、荷重に直すと4Nほどの値が得られた。
試しに、ケーブル破断モデルに入れてみたが、桁が下にたわむ挙動が得られた。
↑50sの様子 (scalefactorは100倍)
↑70s後の拡大図
11/29
Marcの設定を参考にしながら、Salome-Mecaでプログラムを組んでみたが、結果に大きな差がでた。
↑張力を安定させた直後(50s)のモデルの様子 上がりすぎだろ...。
力を安定させた直後(50s)の桁の先端変位の比較
| Marc | Salome | |
| 先端変位(mm) | 2.508 | 4321 |
あまりにもMarcとの差がありすぎるので、試しにMarcで得たビーム軸力をSalomeに入力して50sでの先端変位を見てみると、0.986mmという値が得られた。
↑Salomeで得た張力データを入れた際の先端変位結果
↑Marcで得た張力データを入れた際の先端変位結果
↑Marcの結果
↑70s後の振動の拡大図 Salomeに入力した張力データの結果では70s後の振動はずっとこのような挙動となる。
↑70s後の振動の拡大図 Marcで作成したグラフの70s後の振動はずっとこのような挙動となる。
<ケーブル破断後モデルについて、現時点で考えること>
・当初、Marcの出力結果がkNだと思っていたが、得られた結果を見る限り、その考えは間違っている可能性が高いだろう。(Marcで得られた値を1000倍したらSalomeのFORCと誤差が小さかったのはたまたまの可能性もあるが、全ての値を1000倍したら誤差が数%程度に落ち着いているので、それをたまたまと片づけていいのか個人的には疑問に思う。)
また、SalomeもMarcも張力が[N]で出ていることは分かったので、逆に言えばSalomeで得られたFORC_NODAの値が1000倍掛けた値として出ているとも言えるので、それが何故かを考える必要もある。
FORC_NODAでビーム軸力を得られるなら、何故値がずれるのか考える必要がある。自分の考えでは、ピン接合再現で使ってるバネ要素の線が怪しい? (ちなみに、初期張力はばね要素とケーブルの接合部の節点力を取った。)
仮にSalomeで正しいビーム軸力を得られなかった場合、Marcの軸力の値を使うという手段はある。
⇒張力の見方を改めて考える必要がある。案としては、ケーブルモデルを要素分割して、ケーブルの真ん中あたりの張力(ひとまず、FORC_NODAの合力で)を見てみる。
それか、MULTIFIBERを用いてケーブルモデルの応力を求め、その値に断面積を掛けて力を求めるとか?(MULTIFIBER要素なら、応力を見ることはできるので...)
・力と時間のグラフ
横軸:時間 縦軸:FORCの合力
横軸:時間 縦軸:応力
横軸:時間 縦軸:応力から力に変換
12/6追記
色々探ってみたが、バネと桁の影響を無視してケーブルのみのPRE_EPSIで与えたひずみしか考慮していないため、力が大きく出てしまった可能性がある。(Marcと1000倍値が異なるのは謎だけど...)
一つ思いついた策として、ケーブルをcable要素に変えてやってみる方法である。
ただ、問題点として、salomeのケーブル要素はコンクリートに用いるものを想定している?らしいので、自分の求めている挙動・値が出ない可能性もある。
また、cable要素は温度を考慮した解析をしてくれることは分かったが、温度を時間依存で変化させる方法(横軸を時間にしたtable)が分からない...。(調査不足なので、もう少し調べてみる。)
・Marcの軸力データをsalomeに入力したとしても、50sまでに桁の持ち上がる変位が1mmほど下がっているので、その原因も探る。
ケーブルを2本にして桁を支えたモデルで外側のケーブルを破断させた際の衝撃力を見てみた。
手順としては初期モデルで外側のケーブル(C1)の張力を取って、C1をなくしたモデルに桁の先端に得た張力を掛け、そのときの先端変位・応力・C2の張力を見る。
解析時間は150sで100sまでプレストレスと死荷重を掛け、その後安定させる。
まず、桁の先端変位とC1の張力を取ってみたが、張力はマイナスの値が出てしまった。ちなみに、Marcの結果とほぼ一致した。
先生に意見を頂いたところ、2本のケーブルのプレストレスが同じなのでこのような結果が得られてしまった可能性があるとのことなので、C2のケーブルのプレストレスを少し落としてみる。
| 変位 | 張力 | |
| Salome | 2.50mm | -32.28N |
| Marc | 2.51mm | -32.08N |
↑先端変位
↑張力
グラフの縦軸は桁の先端変位(mm),横軸は時間(s) 119s〜126s間のデータを抽出した.
また、死荷重はFy=-0.017248N/mm,集中荷重は桁の先端にFy=-100Nを掛けている.
・桁1mモデルA,Bの先端変位の動的応答値とDAF
モデルA
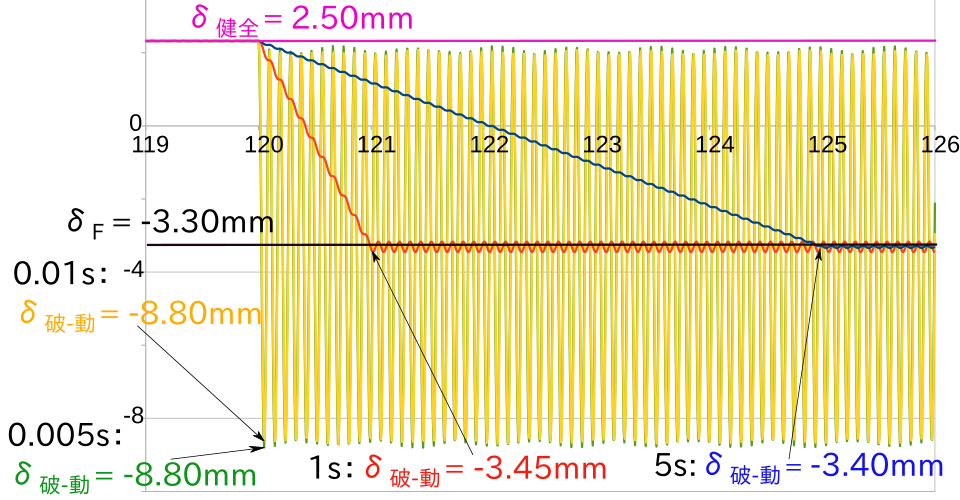
DAF
| 時間 | モデルA | モデルB |
| 0.005s | 1.95 | 1.47 |
| 0.01s | 1.93 | 1.27 |
| 1s | 1.02 | 1.00 |
| 5s | 1.01 | 1.00 |
・桁10mモデルAの先端変位の動的応答値とDAF(モデルBは健全モデルの時点で桁の先端側のケーブルに圧縮が出たので省略.)
DAF
| 時間 | モデルA |
| 0.005s | 2.00 |
| 0.01s | 2.00 |
| 1s | 1.96 |
| 5s | 1.57 |
ただし、120sまでの健全モデルとケーブル破断モデルで桁の先端変位の値が異なっている問題あり。(健全時:24.7897mm,破断時:19.8683mm)
・桁の先端に集中荷重を載荷した桁1mモデルA,Bの先端変位の動的応答値とDAF
DAF
| 時間 | モデルA | モデルB |
| 0.005s | 1.97 | 1.47 |
| 0.01s | 1.95 | 1.27 |
| 1s | 1.03 | 1.00 |
| 5s | 1.00 | 1.00 |
・桁の先端に集中荷重を載荷した桁10mモデルA,Bの先端変位の動的応答値とDAF
DAF
| 時間 | モデルA | モデルB |
| 0.005s | 2.00 | 1.95 |
| 0.01s | 2.00 | 1.95 |
| 1s | 1.96 | 1.26 |
| 5s | 1.57 | 1.04 |
ただし、モデルAについては120sまでの健全モデルとケーブル破断モデルで桁の先端変位の値が異なっている問題あり。(健全時:24.4665mm,破断時:11.9237mm)
○考察
DAFの値としては,1を超えているため大きな衝撃力が発生してると言える。
しかし、桁長10mの場合、健全モデルで得た桁の先端変位と120sまでの破断モデルの先端変位の値が一致していない。
そもそも、健全モデルで得た張力を元々ケーブルがあった箇所に掛けているため、変位の値が大きく変わるということはないはずである。
値が違うということは,何かしら原因があると思うが...。
↑ビーム要素のみのモデル(片持ち梁のモデルは10✕10✕100mmである。)
分かったこと
・1D要素(ビーム要素)で非線形解析を行う際は、Mulifiber(POU_D_EMやPOU_D_TGM)を用いる必要があること。
このページの下から2番目の回答より.
・断面モデルもGeometryで作成してMeshで切る必要がある。(Mulifiberを用いる際、DEFI_GEOM_FIBERを使う必要があるため。)
・結果は_ELGAで見ること。NOEU,ELNOでは結果を見ることができない。
・反復回数や分割数(step数)は細かいほうがよい。(載荷値を増やすことによって、収束しないエラーが出ることがある。)
↑グラフが折れ曲がる付近の拡大図
応力とひずみのデータはこちら 左がひずみ,右が応力
載荷側の断面上の真ん中の球体の応力ひずみデータを取った。
ビーム要素の弾塑性解析の設定方法
DEFI_MATERIAU,DEFI_MATERIAU_GC、どちらでも可。
step数を細かくすると、235MPaで降伏していることが確認できた!
235MPaを超えると、ひずみが大きく増加するので、降伏していると言っていいと思う。(応力で判断するのではなく、ひずみの変化で判断する。)
応力がずっと同じ値で増える理由だが、恐らく周辺の要素(断面を構成している球体)の影響を考慮してないからだと思われる。(逆にソリッド要素は周辺の要素の変化を考慮した応力変化となっているのでは。)
ちなみに、降伏後のひずみだが、降伏後の応力ひずみ曲線の傾き(D_SIGM_EPSI)が小さすぎると大きなひずみ値(5000とか)が出てくるので、降伏後の傾きは大きい数値(1くらい)のほうがよい。
10✕10✕1000mmの片持ち梁で曲げによる弾塑性解析を行い、235MPaで降伏するか確かめた。
ビーム要素
完全固定で設定した節点から応力ひずみ曲線を求めた。
ソリッド要素
Salome-meca
7/24
time0.5sのとき

↑SIEQ_NOEUとEPSI_NOEUを用いた解析結果
グラフの数値はこちら 左側の数値がひずみ 右側の数値が応力
コマンドファイルはこちら
↑SIEQ_NOEUとEPEQ_NOEUを用いた解析結果
グラフの数値はこちら 左側の数値がひずみ 右側の数値が応力
見たところは断面真ん中上で(②)、step数は50分割しています。
SIEQ_NOEUのVMISでミーゼス応力を見れることを知ったので、試しに使ってみた。すると、降伏応力235MPaで曲がるグラフができた!
ミーゼス応力は相当応力とも呼ぶらしく、ひずみも相当ひずみに合わせたほうがいいのかもしれないので、2種類のグラフを作成した。
これらが正しいグラフなのか分からないが(そもそも、何故これまでSIGM_NOEUを使っていたのか理由が気になる。SIEQ_NOEUに何かしらデメリットがあるのでは?)...もしこれが正しい手法であればソリッド要素の弾塑性解析の問題を解決したことになるのでは?
ちなみに、SIEQ_NOEUではミーゼス応力の他にもトレスカ応力や最小・最大主応力や符号付きミーゼス応力も見れる。
後藤メモ(23/9/8):Salome-Mecaのミーゼス応力は、相当応力\( \tilde{\sigma}=\sqrt{3}\overline{\sigma} \)のことだと思う。 \( \overline{\sigma} \)は偏差応力のノルムみたいなもので、1軸引張状態の場合、せん断応力成分の絶対値になる。 せん断降伏応力を\( \tau_{Y} \)と書くと、1軸引張の引張降伏応力\( \sigma_{Y} \)は、\( \sigma_{Y}=\sqrt{3}\overline{\sigma}=\sqrt{3}\tau_{Y} \)と表せるが、ミーゼス応力と(ミーゼス?)ひずみでプロットして、折れ曲がる応力がだいたい235MPa\( =\sigma_{Y} \)になっているということは、Salome-Mecaのミーゼス応力は、相当応力\( \tilde{\sigma}=\sqrt{3}\overline{\sigma} \)になっていると考えられる。 \( \overline{\sigma} \)の方を相当応力という場合もあり(更にはミーゼス応力という場合もあったりするか?)、 この辺は注意が必要である。
このコマンドはCALC_CHAMP→CRETERIAから設定できる.
意味は,相当塑性ひずみ(累積塑性ひずみ)で,EPSIから計算されるとのこと.
ParavisではINVA_2(ミーゼス相当塑性ひずみ)を使えば,相当応力と相当ひずみの応力-ひずみ曲線が作成できると考えている.
ちなみに...相当塑性ひずみとは,各成分の塑性ひずみを用いて計算するものなので,恐らくだが相当ひずみと塑性ひずみを合わせた言葉ではないかと思う.
↑片持ち梁の断面図
メッシュ長さ0.5 要素数394121でメッシュを切った。下の図は固定面の様子

timestepは50分割しており、引張側の真ん中の点が降伏したのがstep20なので、そのときの断面の4隅と引張・圧縮側の真ん中の点をデータをまとめる。
| 降伏応力(MPa) | ひずみ | |
| ① | 264.193 | 0.001099 |
| ② | 238.937 | 0.000947 |
| ③ | 261.468 | 0.001107 |
| ⑤ | -259.924 | -0.001051 |
| ⑥ | -248.081 | -0.000970 |
| ⑦ | -267.69 | -0.001079 |
timestep100の場合(春課題と同じ)
引張側の真ん中の点が降伏したのがstep40
| 降伏応力(MPa) | ひずみ | |
| ① | 264.201 | 0.001099 |
| ② | 238.937 | 0.000947 |
| ③ | 261.412 | 0.001107 |
| ⑤ | -259.925 | -0.001051 |
| ⑥ | -248.081 | -0.000970 |
| ⑦ | -267.692 | -0.001051 |
春課題のデータ
| 降伏応力(MPa) | ひずみ | |
| ① | 249.267 | 0.001042 |
| ② | 234.025 | 0.000936 |
| ③ | 236.751 | 0.000984 |
| ⑤ | -252.657 | -0.001037 |
| ⑥ | -233.743 | -0.000935 |
| ⑦ | -252.314 | -0.001067 |
Marc
↑断面4隅の点を取った場合の応力-ひずみ曲線。4隅どの1点を取っても同じグラフが得られる。(勿論、引張と圧縮側で符号は変わる)
↑②(引張側)の点を取って、応力-ひずみ曲線を求めた。
引張側の真ん中の点が降伏したincrement14で断面の4隅の状況をまとめる.(Increment14: time0.59sのとき)
| 降伏応力(MPa) | ひずみ | |
| ①③ | 240.8 | 0.001451 |
| ② | 236.8 | 0.001186 |
| ⑤⑦ | -240.8 | -0.001451 |
| ⑥ | -236.8 | -0.001186 |
グラフに関してはどうしても上降伏点と下降伏点が現れるグラフになってしまう...
一応,設定している降伏値に近い値であればよいらしいので,多少このようなグラフになるのはしょうがないみたい.
しかし,1つ問題点?があり,固定面からずれた位置のほうが大きな降伏応力が出てしまう場合がある.固定面に一番大きな応力が出るはずなので,これだとおかしい?
②(引張側の真ん中の点)
| 位置 | 降伏応力(MPa) | ひずみ |
| 0mm | 236.8 | 0.001186 |
| 1mm | 248.8 | 0.001116 |
| 2mm | 239 | 0.001091 |
| 3mm | 236.7 | 0.00114 |
4隅(数値は絶対値で表記)
| 位置 | 降伏応力(MPa) | ひずみ |
| 0mm | 240.8 | 0.001451 |
| 1mm | 237.9 | 0.001304 |
| 2mm | 236.6 | 0.001117 |
| 3mm | 238.3 | 0.001098 |
↑②(引張側)の点を取って、応力-ひずみ曲線を求めた。
↑①,②,③の応力-ひずみ曲線をまとめたグラフ
↑④,⑧,⑨の応力-ひずみ曲線をまとめたグラフ
↑⑤,⑥,⑦の応力-ひずみ曲線をまとめたグラフ
・上降伏点と下降伏点が現れるグラフができた。
グラフとしては間違っていないが、設定した降伏応力を超えないようにしたいのでこれではダメみたい…。
ビーム要素
ソリッド要素
| 解析ツール | 降伏応力(MPa) | ひずみ |
| Salome | 238.937 | 0.000947 |
| Marc | 236.8 | 0.001186 |
4隅のデータ
Salome-meca
| 降伏応力(MPa) | ひずみ | |
| ① | 264.193 | 0.001099 |
| ③ | 261.468 | 0.001107 |
| ⑤ | -259.924 | -0.001051 |
| ⑦ | -267.69 | -0.001079 |
Marc(数値は絶対値)
| 降伏応力(MPa) | ひずみ |
| 240.8 | 0.001451 |
Marcのビーム要素でできるグラフ(指定した降伏応力で曲がるグラフ)を作りたいと考える。
どちらも降伏応力はそれなりに近い値が出るが、グラフ形状が大きく異なる。
Salomeは指定した降伏応力を設定しても応力がずっと増えていってしまう。(降伏点は確認できるが、それでも設定した値より大きな値で曲がる。)
一方、Marcは上降伏点と下降伏点が現れるグラフができるが、上降伏点は設定した降伏応力より大きく離れていない上に最終的には設定した降伏応力に落ち着くので許容範囲として扱ってもいいだろう。
が、固定面の応力より固定面から離れた位置のほうが少し大きな応力が出ることについては疑問に感じる...。(曲げモーメントで考えると、固定面は一番応力が大きいはず。)
また、4隅のデータについてだが、Salomeは4隅のデータそれぞれバラバラに対し、Marcは全て同じ値(絶対値として一致)が出た。断面は10✕10mmなので、対称部材であることを考えると同じ値が出ないとおかしいはずだが...。
現段階で言えることは、ソリッド要素の弾塑性解析はSalome-mecaでのやり方を見直す必要があるだろう。降伏に達した後も応力がずっと増え続けるグラフを何とかしたい...。まず、Aster_codeの弾塑性解析に関わるコマンドの説明書を読んで、何か解決策がないか模索する。
(追記:一旦、ビーム要素の弾塑性解析を重視で行っているので、こちらの作業はひとまずストップします。)
片持ち梁曲げの解析方法は以下の通りに行なった。(一部、Marc_Mentatメモを引用して作成)
形状設定
テーブルと座標系
ちなみに、バイリニアだとここで応力ひずみの値を入れる必要はないが、入れる場合はタイプをplastic_strain → データポイントを追加する。(最低、2点は必要)
なお、最初の点の塑性ひずみは0でその時の応力が降伏応力である。(0,235)だと降伏応力の数値は235である。
材料設定
境界条件設定
解析
結果見る
形状設定より先の設定は梁要素と同じなので、それより前の設定を述べる。
形状設定
ここからの設定は梁要素と同じです。注意点として、境界条件で荷重を設定する際に集中荷重を用いる場合、1点あたりの荷重を掛けることになるので、かける荷重を節点の数で割った値を入力すること。 (例:点が100個あって、荷重を800N掛けるなら、入力値は8)
5/19(金)遅くなりましたが、Tutorial9,10視聴完了。Tutorial9は減衰を伴う梁の周波数応答解析、10は複合材料(鉄筋コンクリート)の断面モデリングの内容でした。後は自分のパソコンで解析をして、動画と同じように解析できるか試します。
5/4(木)Tutorial8視聴完了。内容は高調波ベース加振を受けるDOFシステムでした。この手法は耐震解析にも有効だそうなので、大事なところかなと思います。
4/30(日)Tutorial7視聴完了。内容は非減衰MDOFシステムの周波数応答解析でした。
4/27(木)Tutorial4で使用したモデルを作成し、動画と同じ挙動になることを確認した。Tutorial5は動画のようなグラフの出し方が分からない(XMGRACEに対応していない)ので、一旦ストップ。
4/26(水)Tutorial6視聴完了。内容はMDOF法(多自由度振動系)のモーダル解析でした。最近、salomeの解析に手が回っておらず、T4~T6までを実際に解析を回してなかったので、今週中に取り組みます。
4/24(月)Tutorial5,5A視聴完了。内容はSDOF法(1自由度系の振動系)のモーダル解析でした。この解析手法が振動系を考える上での基本らしいので、今視聴した範囲では一番重要なところかなと思います。
4/21(金)Tutorial4視聴完了。片持ち梁のモード解析の内容だった。今まで使ったことのないコマンド(Pre analysis:ASSEMBLAGEなど)が出てきたので、よく勉強しようと思います。
4/13(木)Tutorial2B,3視聴完了。データの保存方法(.resuファイルの作り方と見方)・MACR_CARA_POUTREを使ってTutorial2と同じ解析を行う内容だった。MACR_CARA_POUTREは断面性能を計算する際に用いるコマンドらしい。
4/11(火)Tutorial2で使用したモデルを作成し、動画と同じ挙動になることを確認した。今後、動画視聴→実際にsalome解析するという流れで作業を行なっていく。Tutorial2Bも現在視聴中。
4/8(土)Tutorial2 一通り視聴完了。点と線で片持ち梁モデルを作り、梁の先端に荷重をかける内容だった。自分のパソコンで実際に解析できるか試してみる。
ここでは自分が学んだSalome-mecaの知識についてまとめる。ビーム要素(1Dモデル)関連の話がメインなので、2D,3Dモデルの話は少なめです。
code-aster名称http://opencae.gifu-nct.ac.jp/pukiwiki/index.php?Salome-%A5%D5%A5%E9%A5%F3%A5%B9%B8%EC%C2%D0%BA%F6(このURLに載っているExcelファイルに更に詳しく書いてあります。)
1D要素で弾塑性解析を始めとした材料非線形の解析を行う場合は、POU_D_EM, POU_D_TGMを用いる必要があり、これらの要素にはビーム断面を作成してビームモデルに適用する必要がある。
(1)DEFI_GEOM_FIBER
まず、このコマンドを使う前にビーム要素の断面として使う断面モデルをGeometryで作成、Meshを切り、LIRE_MAILAGEで適用すること。
SECTIONは断面定義、FIBREは断面の穴あき部分を定義する?(例えば、鉄筋コンクリートの断面モデルを作成する際、鉄筋を入れるところはcutして空白部分をつくり、そこをFIBREで当てはめていた。)
ビーム断面が厚肉断面もしくは空白部分に何も入れる必要がなければ、SECTIONだけでよい。
TOUT_SECTはビーム要素に作成した平面モデルを全て適用したい場合にチェックをいれる。
GROUP_FIBERは好きな名前をつけてよい。
MAILAGE_SECTはLIRE_MAILAGEで適用した平面モデルを選択。
COOR_AXE_POUTREとANGLEは0でよい。
(2)AFFE_CARA_ELEM
GEOM_FIBREが適用されていることを確認して、MULTIFIBREの選択。GROUP_MAは自分のつくったビーム要素を選択し、GROUP_FIBREは(1)で設定した名前と同じ名前を記入。後はAFFE_MODELEで適用した設定に合うコマンド(POUTREなど)を設定すること。(例:MULTIFIBRE+POUTRE)
(ただし、AFFE_MODELEで_*Mと書いてあるキーワードを設定すること。詳細はAFFE_MODELE(1)参照)
(3)DEFI_COMPOR
ここでは断面の材料特性と状態(弾塑性を入れるとか)を定義する。
このコマンドは画面上の{a}+の横にある{}+(Show All Commands)をクリックして、DEFI_COMPORと検索すると出てくる。
スクロールして探すなら、Otherの欄にあるので、それを選択してクリック
適用すると、下図のような画面が現れるが、GEOM_FIBREはDEFI_GEOM_FIBERを適用する場所、MATER_SECTは断面に定義する材料特性である。
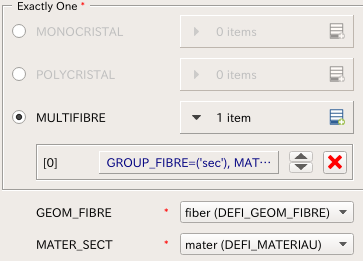
MULTIFIBREを選択したら、GROUP_FIBREは(1)と同じ名前,materはDEFI_MATERIAUで設定したものを適用、RELATION(構成則)は弾塑性(VMIS_ISOT_とか)などを入れることができるので、自分が入れたいものを選択する。(STAT_NON_LINEのCOMPORMENTで設定するRELATIONはMULTIFIBREにすること。)
最後に、DEFI_COMPORをAFFE_MATERIAUのAFFE_COMPORで適用するのを忘れずに行うこと。
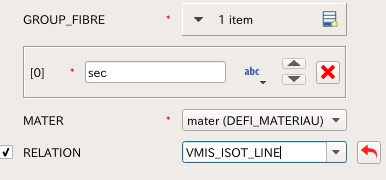
・注意点
(1)DEFI_FONCTIONとAFFE_CHAR_MECAは、Pre Analysis・Analysis用とPostprocessing用に分けること。また、名前も変えるのも忘れないように。
(2)DISCRETに質量マトリクスを用意しておくこと。DISCRETには質量を入れられないので、M_TR_D_LにVALE0を入れる。これでDISCRETの質量マトリクス計算を無視することができる。
この設定をしないと、ASSEMBLAGEでバネ要素に質量マトリクスを定義しようとするので、エラーがでる。
詳しくはこちらを参照
(3)DYNA_VIBRAとCALC_CHAMPの名前は同じにすること。(同じ名前にしないと、何故かエラーが出る。理由は不明。)
(4)CALC_CHAMPのEXCITにDYNA_LINEで設定したCHARGEの分だけ入れること。(ちなみに、DYNA_NON_LINEではこの作業は必要ない。)
設定方法
[1]Pre analysisのASSEMBLAGEを選択
・ここでやること
①NUME_DDLは{}押し、nddlと入力。
②MATR_ASSEで質量マトリクスと剛性マトリクスを定義する。(質量マトリクスはMASS_MECA,剛性マトリクスはRIGI_MECAを選択。MATRICEは好きな名前でOK.)
③CHARGEはAFFE_CHAR_MECAで適用した境界条件分だけ追加する。
[2-1]AnalysisのDYNA_LINEを選択
・ここでやること
①BASE_CALCULをPHYS,TYPE_CALCULをTRANに設定する。
②EXCITに載荷条件(PRE_EPSIも同様に)の設定を適用。DEFI_FONCTIONで作ったテーブルもこちらに適用すること。CHARGEには境界条件(DDL_IMPOで作成したもの)を適用すること。
③SCHEMA TEMPSでNEWMARK,BETAを0.25と設定する。
④INCREMENTはDEFI_FONCTIONで作ったテーブルの時間に合わせる。自分の場合は100sまでのテーブルを作成しているので、INST_FINを100s,INST_INITを0s,PASを0.1に設定した。
ビーム要素なら、CARA_ELEMにチェックを入れること。
[2-2]DYNA_NON_LINEの場合
ここで弾塑性を入れた動的解析ができると思われるが、そのあたりの設定をまだ把握してないので、分かり次第追記します。
・最低限やること
①SCHEMA TEMPSでNEWMARK,FORMULATIONをDEPLACEMENT(変位),BETAを0.25と設定する。(ニューマークβ法の設定)
ちなみに,説明書の11ページを見ると,ニューマークは時間積分を行なっているとのこと。
更に詳しく調べると,これは直接積分法(正確には直接時間積分法)の陰解法と呼ばれているらしい。
(Marcもニューマークβ法を用いて連鎖崩壊に関する解析をしていたので,名称はこれで間違っていないはず。)
参考サイト
②INCREMENTはDEFI_LIST_INSTで設定したものを選ぶ。
③EXCITにAFFE_CHAR_MECAで作成した数だけ設定する。載荷条件にはDEFI_FONCTIONで作成したテーブルを適用するのを忘れずに
ビーム要素なら、CARA_ELEMにチェックを入れること。
[3]Post ProcessingのCALC_CHAMPを選択
・ここでやること
①CALC_CHAMPの名前をDYNA_LINEと同じ名前にすること!これをしないと、エラーが出る!
②EXCITにAFFE_CHAR_MECAで適用した境界条件分だけ追加する。ここで追加するのはCALC_CHAMP用に分けた境界条件を追加。掛けている荷重に適用するDEFI_FONCTIONもCALC_CHAMP用を選択。
モデルをひずみを用いて変形させることができるコマンドである。
1Dモデル(Multifiber要素も含む)ではEPX(梁のローカル軸に応じた伸びの要素別定数値),3DモデルではEPXX,YY,ZZ,XY,XZ,YZに値を入れる。
(ky,kzはたわみの微分方程式から得られるdθ/dx = -M/EI の値を入力する。使う必要があるなら入力する。ちなみに、式を見ると、kyは-dθ/dx,kzはdθ/dx とのこと。)
X,Y,Zの軸の向きはグローバル座標(salome画面の色がついてる座標)にあたるもので、正の値を入力すると伸び、負の値だと縮む。
単純梁モデル(10✕10✕120mm)にEPXX:0.01を与えると、以下の挙動が得られた。(Scalefactorは10倍にした。)

線に色がついてるところが変形前のモデルの端であり、写真を見るとモデルが伸びていることが分かる。
・簡易モデルに用いた際に分かったこと
現在、ケーブルにPRE_EPSIを入れており、縮む挙動(ケーブルが桁を引っ張るようにする)をみる場合、ひずみの値に-をつける必要があるが、それだと応力がマイナスの値が出てしまう。(σ=Eεよりεがマイナスの値を与えているため)
その理由について考えてみたが、要素を構成している節点にモデルを縮ませるような負荷を与えるように力を与えており、その内力(抵抗力)を応力としてSalomeが計算しているのではないかと推測した。(説明書に変形の負荷と書いてあるので、与えたひずみになるような外力をPRE_EPSIの設定をしたモデルに掛けているのでは?)
↑PRE_EPSIの意味 日本語に訳すと要素に変形の負荷を与えるみたい。ちなみに、文字化けしているところはεが入っている。
↑簡単な例 PRE_EPSIで与えたひずみになるような外力をかけて、青い矢印(内力)の向きの応力を見ている可能性がある。
(1)マウス操作について
マウスホイールを動かす or ctrlキー+マウス左クリック押し続ける:拡大,縮小
ctrlキー+マウスホイールを押し続ける:移動
ctrlキー+マウス右クリック押し続ける:回転
(2)つくったモデルを消さずに長さ等を調整する方法
作成したモデルの長さなどを変えたいとき、わざわざ作り直さなくてもviを用いて調整することができる。
Geometryで左上のファイル→スクリプトの保存→ファイルの種類が.pyになっていることを確認して保存→viで保存したファイルを開く
すると、下図のような画面が現れるので、点の位置や線の長さなどを好きなように調整する。調整後は、Geometryで左上のファイルでスクリプトの読み込みで調整したモデルを適用できる。
(1)メッシュのcompoundについて
Meshにもcompound機能があり、別々に切ったメッシュを1つにくっつけることができる。(メッシュ→アセンブリをビルド または、画面✕2と書いてあるマークの左をクリック)
これを使えば、Marcの簡易モデルと同じメッシュの切り方ができる。(簡易モデルについては自分の簡易モデルのページを参照)
・MACR_CARA_POUTREとDEFI_GEOM_FIBERの違い~ どちらのコマンドもビーム要素の断面特性を定義できるが、MACR_CARA_POUTREではねじれ,反りの慣性、ねじれ中心の位置を計算することができる。(DEFI_GEOM_FIBERではこれらの計算はできない。)
・AFFE_MODELEとAFFE_CARA_ELEMの対応コマンド
AFFE_MODELEで設定したmodelisationはAFFE_CARA_ELEMのコマンドに適用できるものを選ばないとエラーがでる。
対応しているものを以下にまとめたので、参考にしてください。
POUTRE:POU_D_E, POU_D_T, POU_D_TG, POU_D_T_GD, FLUI_STRU, TUYAU_3M,TUYAU_6M, POU_D_EM, POU_D_TGM
BARRE:BAR, CABLE_GAINE
CABLE:CABLE, CABLE_POULIE
COQUE:COQUE_AXIS, COQUE_C_PLAN, COQUE_D_PLAN, DKT, DST, DKQ, DSQ,Q4G, COQUE_3D, DKTG, Q4GG
DISCRETE:DIS_T, DIS_TR
DISCRETE_2D:2D_DIS_T, 2D_DIS_TR
MULTI_FIBRE:POU_D_EM, POU_D_TGM
・AFFE_MODELE ビーム要素でのMODELISATIONの選び方
梁の種類によって、選択するものが異なる。
・真っ直ぐな梁:POU_D_E(オイラー梁), POU_D_T(ティモシェンコ梁)
・マルチファイバーの梁(鉄筋コンクリートや非線形材料の解析に使う。)POU_D_*M [*にはEやGなどが入る]
・棒(鉄筋とか断面が円のもの?) 2D_BARRE, BARRE 引張と圧縮応力が見れる
・ケーブル CABLE 引張荷重 (引張だけ出せるが、斜張橋などのケーブルのような挙動ではなく、コンクリートのプレストレスなどを再現するのに使われるコマンド)
・AFFE_CARA_ELEM DISCRETの使い方
DISCRETは離散という意味でバネ要素を定義する場所である。ここではバネ要素に対するマトリクスを与えることができる。
アルファベットの意味
A:減衰
K:剛性
M:質量
T:並進運動
TR:並進運動&回転
D:対角行列
L:線
N:節点
↑K_TR_D_Lにした場合の設定画面
VALE[0],[1],[2]は変位に対する剛性(0,1,2の順にx,y,z方向を示す.),
[3],[4],[5]は回転に対する剛性(3,4,5の順にDRX,DRY,DRZを示す.)
GLOBALはグローバル座標,LOCALはローカル座標を示す。
(1)AFFE_CHAR_MECA DDL_IMPO 完全固定の別のやり方
これまで完全固定をする場合、DX=DY=DZ=0と設定していたが、LIAISON=ENCASTER(全自由度拘束)でも設定可。
(2)AFFE_CHAR_MECA FORCE_の意味
FORCE_NODAL ノードあたりの力
FORCE_FACE 1面あたりの力
FORCE_ARETE エッジ1本あたりの力(1D要素では使えなかった。)
FORCE_CONTOUR 輪郭の長さあたりの力
FORCE_POUTRE 梁の長さあたりの力
ELGA:ガウス点のelementごとに応力または力またはモーメント
ELNO:node点におけるelementごとの応力または力またはモーメントを意味する。
EFGE_ELNO:要素ローカル軸の節点における要素ごとの力またはモーメントを意味し、SIEF_ELNOと同じ成分を含んでいる。
・CALC_CHAMPとCREA_CHAMPの違い
CALC_CHAMP を使用して、既存のデータからデータ構造を計算します。
CREA_CHAMP を使用して新しいフィールドを初期化し、後で分析式を使用してデータを入力するか、既存の結果から計算します。
CREA_CHAMPでは、構造物にどれだけ温度を与えるか設定できる。(弾性のコマンドとかあるから、他の使い方もできそうだけど...。)
・このエラーメッセージは構造的に不安定なときに出る。
これが出た場合は基本的にAsterstudyの設定を間違えていることが多いので、まずは設定を見直そう。
・AFFE_CHAR_MECAの設定をモデルに適用できない場合に出る。自分の場合は1D要素(ビーム要素)にFORCE_ARETEを適用しようとしたらエラーがでた。
・AFFE_MODELEとAFFE_CARA_ELEMの条件が一致しない場合に出る。
AFFE_MODELEで設定したMODELISATIONは、それぞれAFFE_CARA_ELEMに対応するものが必ずあるので正しいものを選ぶこと。
(例) AFFE_MODELEでBARREを選択した場合→AFFE_CARA_ELEMではBARRE
AFFE_MODELEでPOU_D_Eを選択した場合→AFFE_CARA_ELEMではPOUTRE
(1)評価項目(magnitudeとか選択するところ)について

magnitude:全項目のΣ2乗の平方根(ただし、DEPLだけは変位量の合計っぽい)
DEPLのDX:X方向変位量
SIGM_NOEUのSIXX:X方向垂直応力
SIGM_NOEUのSIXY:XYせん断応力
SIEQ_NOEUのVMIS:ミーゼス応力(ちなみに、ミーゼス応力とは垂直応力とせん断応力から計算されるスカラー量の応力。)
今載せたのは一例だが、他にもこのページにDEPL,SIGM,SIEQの説明が色々書いてある。
(2).csvファイルの数字とParavisの評価項目
.csvファイルの1行目の()の数字(例えば,DEPL(0)とか)はPavarisの評価項目と対応している。
例を挙げると、SIGM_NOEUの場合、SIXXはSIGM_NOEU(0),SIYYはSIGM_NOEU(1),SIZZはSIGM_NOEU(2),SIXYはSIGM_NOEU(3),SIXZはSIGM_NOEU(4),SIYZはSIGM_NOEU(5)に対応している。
久し振りに使うとコマンド等を色々忘れているので、ここにメモしておきます。
(1)余白の埋め方
入れる場所はタイトルや名前を書くところより上に(こんな感じに)
{0pt}にすると余白がなくなる。図などを貼り付けた際にできる余白が気になるなら以下のコマンドを入れる。
\setlength\textfloatsep{0pt} %本文と図の間の余白
\setlength\floatsep{0pt} %図と図の間の余白
\setlength\intextsep{0pt} %本文中の図の余白
\setlength\abovecaptionskip{0pt} %図とキャプション(図や表の名前)の間の余白
(2)画像の貼り方
ファイルの語尾が.pdf_texの場合(inkscapeで編集したグラフなど)は、\scalebox{倍率(数値入れる)}{\input{ファイル名.pdf_tex}}を入力。
.png(スクリーンショットした画像など)の場合、\includegraphics[width=数値mm]{ファイル名.png}を入力する。
(3)数式について
数式で表すには$で挟む必要がある。
(例)
・研究活動で使う参考資料
code_asterの動画 (音声は英語だが、内容は振動解析に関わってくるもの。)
code-asterの説明 (英語で書かれているので翻訳する必要あり)
CAE用語辞典(解析の種類などの意味を調べるのに使う)
例題で学ぶMarc有限要素法解析入門 (2013年に出版されたものなので、少し違いがあるかもしれない。なお、閲覧にはAUアカウントとPW必要)
Salome-Mecaのチュートリアル (英語だが、Salome-Meca全体の話が色々載っている。例えば、作成した構造物に適した要素(3D,BAR...etc)とか)
Salome-meca beginning with code_aster (Salome-mecaの質問するところ[掲示板]でよくこれを見てくれと答える人が多いので、載せてみた。英語で書かれている。)
・UNIXコマンド一覧 リンク集
https://www.str.ce.akita-u.ac.jp/~gotou/linux/vine.html#unix
https://proengineer.internous.co.jp/content/columnfeature/2669
https://amorphous.tf.chiba-u.jp/lecture.files/seminar-I/unix/01unix-command.pdf
・弾塑性解析
春課題で行なった弾塑性解析については以下のURLにまとめてあります。
3/31(日)
3年生から更新してきた卒論日誌も本日で最終更新です。明日からいよいよ4月となり、院生としての生活が始まります。
これからの2年間、色々なことが待ち受けていると思いますが、楽しく過ごしていきたいと思います。
そして、これまで鋼橋の研究をされていた先輩方という自分にとっては目標となる人達がいますので、自分も先輩方みたいな学生に近づけるように自分なりに考えて勉強に研究活動を頑張ります!!
3/22(金)
卒業式が無事に終了しました。今日で3年生の後期からずっと一緒に過ごしてきた仲間たちと何人かはお別れになります。ここまで一緒にいて楽しくて、お別れするのが寂しいと思ったのは初めてだな...。
けど、またいつかどこかで会う機会はあるはずです。そのときには、お互いに成長した姿を見せることになると思うので、自分もこれからの院での生活を通じてもっともっと成長していきたいと思います!
3/8(金)
無事に謝恩式が終了しました。皆さんが協力していただいたおかげで無事に開催もできて、終える事ができたので、本当によかったと思います。
挨拶のとき、皆さんの前に立ったとき、緊張もありましたが、色々思うことがあって、何度か言葉が出てこなくなってしまいました...。感動するってこういうことなんだな、ほんと、秋田大学で土木を学ぶことができてよかったな...。
秋田での生活はまだまだこれからも続きますが、まずは卒論本体完成,引き継ぎをしっかり行なって、来年度に備えたいと思います。
来年度から鋼橋の研究する先輩が誰もいなくなるから、自分がしっかりしないとね...(・・;)
2/21(水)
久々の更新です。卒論発表が無事に終わり、先生方からの評価も頂きました。
そしたらなんと、学部生の中では1番良い評価をいただいたので、自分でも非常にびっくりしました。...嘘だろ(・・;)
ただ、自分の研究成果はまだまだ途中段階ではあるし、まだこれで終わりというわけではないので、いい評価を頂いたからと言って油断することなく、4月からの修士でも頑張って研究に取り組んでいきたいと思います。
12/31(日)
2023年も残りあとわずかです。
今年も色々ありましたが、楽しく過ごすことができました。
特に今年は自分のことを色々見直す機会が多く、もっと人として成長しなきゃいけないなと思いました。
来年は1月から3月にかけて、卒論に東北支部、それに謝恩会の準備とやることがたくさんありますが、一つ一つしっかりとこなしていきたいと思います。
2024年はどんなことが待っているのだろうか…
来年もよろしくお願いしますm(_ _)m
11/28(火)
11月ももうすぐ終わり...早いな(・・;)
来月でいよいよ2023年も終わり、中間発表に卒論が近づいてきています。
卒業できないということはないと思うけど、このままだと面白くない発表になってしまうので焦りを感じています。
残りの時間でどこまでやれるか分かりませんが、先生方や先輩方の知識や力をお借りしながら、自分のできる限りを尽くして、まずは12月を乗り切りたいと思います!
11/17(金)
今日、創造工房実習でSalome-Mecaを教えました。
皆さんの前で立って教えましたが、人にわかりやすく教えるのは難しいなと改めて思いました。
あの説明で、ある程度理解することはできたのだろうか...。
次は前で教えることはありませんが、反省点もいくつか見つかったので、周りで教える際はその反省を活かして教えればいいなと思います。
11/5(日)
10月下旬あたりからずっと考えていたプレストレス問題だが、どうやら動的解析にはプレストレスを適用できないことが分かった...。
何で線形静的解析でしかできない(対応していない)のか不思議だが、卒論まで時間もなくなってきているので、その問題は卒論が終わった後にでも改めてじっくり考えてみることにする。
...卒論まで残り3ヶ月だし、いい研究成果が発表できるように頑張らないとな。
10/24(火)
家の近くに熊が出没するという中々恐ろしいことがありました。ほんと近いうちに遭遇するかもな...(^^;
思えば10月も来週で終わり、時が経つのが早いなと感じます。
来年の4月から就職する同級生や先輩と過ごすのもあと半年もありません。1日1日を大事に過ごさないといけないなと思います。
10/20(金)
ようやく家のネット環境が復帰して、早速自宅で日記を書いています(^^;
…さて、今日は構造研に配属された3年生と顔合わせをしました。
3年生達の姿を見て、去年の自分達もこんな感じだったのかなと思うと懐かしく思います。ここにきて、もう1年経ったんだよな…。
自分は大学院に進むので、少なくとも1年半は一緒に過ごすことになるので、仲良くできたらいいなと思います。
よろしくお願いしますm(_ _)m
10/18(水)
本日、3年生の研究室配属先が決まったそうです。
すでに何人かは顔合わせをしましたが、全員での顔合わせは今週の金曜日になるそうなので、どんな人が来るか楽しみです!
同時に、自分もしっかりしなきゃいけないとも思います。
卒業された先輩方や今の院生のようにちゃんとサポートできるように頑張りたいと思います!
10/11(水)
学部生での研究活動も後半戦、他の研究室でもそろそろ卒論に向けて本格的に取り組み始めている頃かな...?
いよいよ今週末に3年生も研究室に入ってくるので、悪い手本にならないようにしないとなと思っています。
ただ...最近、細かいミスをしたり、人の話を1回で正しく理解できていないことが結構あるなと感じています...。
あまりこういう状況が続くのはさすがにまずいと思う(場合によっては他の人にも迷惑をかけるし...)ので、休むときはしっかり休んでやるときはしっかりやるというメリハリをつけて研究に取り組みたいと思います。
9/29(金)
中間発表が無事に終わり、そして夏休みも終わりました。
発表に対しても初めて発表をした2月の頃と比べると成長したなと感じることができました。
...少しは変われたかな?
来週から後期が始まりますので、引き続き研究に取り組みたいと思います。...とはいっても、授業はとっていないので何か変わるわけではありませんが(^^;)
9/12(火)
今週は昼過ぎまで集中講義を受講し、夕方から研究をするという日程で過ごしています。
calculixでプログラムを作っている最中で、どうしても分からないところは除いて一通り作成したら、先生方に見てもらおうと考えています。
それでも簡易モデルの再現ができなければ、どうするべきか相談しないとな...。
9/8(金)
昨日は帰ってきて何もせずに寝てしまったので、部屋の掃除や帰秋後の片付けなど元の生活環境に戻す準備を行なっていたため、研究室に来るのが夜になってしまった...。
ひとまず、実家でやっていたデータを研究室のパソコンに移した(とはいっても、あまり進展がないが...。)ので、明日からは研究室メインでの活動に戻ります!
中間発表までは、平日は解析をメインで、休日は概要とスライド作成をメインに行なっていこうと思います。
9/7(木)
今日、秋田に戻ってきます。
実家での夏休みは父の実家に行ったり、インターンシップに参加、友人と会ったり等充実した日々を過ごすことができました。(お盆明けあたりで夏バテで1週間くらい体調を崩してしまったことは反省しないと...)
秋田に戻ったら、再び研究一筋の日々になりますが、卒論に向けて頑張っていこうと思います!
8/6(日)
秋田は竿燈祭りで盛り上がっています(^^)
自分は平日に見に行ったので、昨日今日はのんびり過ごしつつ実家に戻る前の準備をしています。(解析用のノートパソコンを借りることができたので、その準備もしました。)
後は...台風がどうなるか心配です。無事に帰省できるといいけど...(^_^;)
8/2(水)
前期のゼミは本日で終わりました。...早いな(^_^;)
Salomeを使えるノートパソコンを借りることができ、これで実家でも解析ができるので引き続きピン接合問題の解決に向けて取り組みます!
ちなみに、明日から竿燈祭りがあるらしいです。人はたくさん来るけど...去年みたいに少し離れた場所からでも見ようかな。(大通りは人が多すぎて入れないし...)
7/26(水)
久々の更新です。(4月〜7月の日誌はwikiの整理の際に消してしまいました...。)
今日、外国語文献の講義での発表が終了しました。質問の際、言ってることを理解できていても自分の言いたいことを上手く伝えることができなかったケースが何回もあったので、単語知識が不足しているなと感じました。
けど、4月のときより聞き取る力は上がっていると思うので、英語の勉強は引き続きやっていこうと思います。...また来年再チャレンジしようかな(来年以降は単位関係なく参加できます)
気が向いたら、こんな風に更新していこうと思います。
2/3(金)
課題は完成しました。後はスライド作りをするのみです。(現在、スライド構成に悩み中)
1/31(火)
一通り確認し、後はサンドウィッチ梁の考察について思うところがあったので、そこを改めて考えて完成です。
1/27(金)
概要は提出できる状況までできましたが、提出期限まであと1週間あるので見直しをしていきます。
今日からスライド作成に入りたいと思います。(2/10までには完成させる必要あり、余裕を持って2/8までに終わらせたい。)
1/26(木)
まとめまで一通り書き終えました。後は図の配置や適切な大きさに変える等の編集、誤字脱字やおかしいことを書いてないかなどの見直しを行います。
1/24(火)
異方性2次単純梁の解析完了。サンドウィッチ梁について書く材料は揃ったので、サンドウィッチ梁について書く、まとめを作成、そして必要なグラフと図を貼り付ける。
1/23(月)
異方性2次単純梁の解析を行っている途中である。(サンドウィッチ梁の比較で使うため。) 後、LaTeXに貼り付けた図の位置がいまいちなので、調整すること。
1/20(金)
解析結果と考察を1つにまとめることにした。
残りの作業は解析結果と考察に関してはサンドウィッチ梁を書くのみ、まとめの作成、課題で作成した表とグラフの貼り付け、必要な図の作成を行う。後、図2の大きさ編集を行う。
1/17(火)
論文の構成を変更(はじめに→材料性質と解析方法→解析結果→考察→まとめ)
はじめに、材料性質と解析方法を一通り書いた。(図の作成はinkscapeを使ってこれから行なっていく。)
1/16(月)
創造工房実習の課題の解析結果を一部編集しました。(単純梁と異方性)
解析結果の編集に入りました。
1/13(金)
課題で使う全てのグラフをinkscapeで修正しました。
とりあえず、課題の論文の構成は(はじめに→解析結果→考察→まとめ)にする。(sibup2を使って作成していく。) また、論文のタイトルと名前の修正を行い、「はじめに」の部分を一応完成させた。
1/11(水)
wikiに貼り付けたグラフをsvgに変換させました。
メモ:inkscapeで凡例のみを消す方法はグラフをノードツール(画面左側にある黒矢印の下、もしくはキーボードのF2)でクリックして、画面上部にあるパス→分解を選択。すると、グラフ線と凡例が別々に分かれるので、これで凡例だけ消すことができる。なお、分解した際に色が消えたら、グラフ線をノードツールでクリックして、ストロークの塗りで色を付けることが可能。
異方性の単純梁(1次)と2次要素のサンドウィッチ梁(鋼材:等方性 木材:異方性)の比較
2次要素のサンドウィッチ梁のデータ
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 583289 | - | - | 千代岡 |
| 0.6 | 214850 | - | - | 高井 |
| 0.7 | 155266 | 0.0861 | -13.0 | 関合 |
| 0.8 | 138453 | 0.083487 | -15.7 | 岡田 |
| 0.9 | 82766 | 0.083312 | -15.8 | 松田 |
| 1.2 | 32279 | 0.083574 | -15.6 | 青野 |
| 1.3 | 28343 | 0.083668 | -15.49 | 山口 |
| 1.4 | 23667 | 0.083680 | -15.48 | 山本 |
| 1.5 | 19958 | 0.083516 | -15.6 | 進藤 |
| 1.6 | 19451 | 0.086037 | -13.1 | 河合 |
| 1.8 | 10933 | 0.084022 | -15.13 | 山口 |
| 2 | 10764 | 0.083324 | -15.8 | 進藤 |
| 3 | 3618 | 0.083497 | -15.66 | 山本 |
| 4 | 1623 | 0.0852 | -13.9 | 関合 |
| 5 | 1007 | 0.083104 | -16.1 | 千代岡 |
| 6 | 842 | 0.0821 | -17.1 | 高井 |
| 7 | 554 | 0.080750 | -18.4 | 青野 |
| 8 | 289 | 0.079715 | -19.5 | 岡田 |
| 9 | 261 | 0.078427 | -20.78 | 松田 |
| 10 | 232 | 0.082495 | -16.67 | 河合 |
異方性1次単純梁と2次要素サンドウィッチ梁の比較グラフ (ihou2:11/25の異方性1次解析のデータ ihouriron2:異方性1次の理論値0.4917mm sand2ji:2次要素のサンドウィッチ梁 sandrironti:サンドウィッチ梁の理論値0.099mm)
メモ:鋼材を挟むのと挟まない場合では理論値が約5倍異なり、サンドウィッチ梁のほうが変位は小さくなる。また、解析できた範囲で考えると、変位は0.083±0.003mmの範囲内にほぼ収まっている。しかし、メッシュ長さ0.5,0.6での解析は要素数が大きすぎて解析できなかったので、値がサンドウィッチ梁の理論値にもっと近づく可能性もある。(グラフを見ると、要素数140000~160000の間で少し右肩上がりになっている。)
2次要素の異方性単純梁のデータ
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) |
| 0.5 | 604167 | - | - |
| 0.6 | 202805 | - | - |
| 0.7 | 145019 | 0.516 | 5.1 |
| 0.8 | 141896 | 0.515 | 4.8 |
| 0.9 | 91974 | 0.514 | 4.6 |
| 1.2 | 24520 | 0.512 | 4.1 |
| 1.3 | 23810 | 0.512 | 4.1 |
| 1.4 | 17725 | 0.511 | 4.0 |
| 1.5 | 15433 | 0.511 | 3.9 |
| 1.6 | 15746 | 0.510 | 3.7 |
| 1.8 | 11647 | 0.509 | 3.5 |
| 2 | 10460 | 0.509 | 3.5 |
| 3 | 2298 | 0.504 | 2.5 |
| 4 | 1482 | 0.500 | 1.6 |
| 5 | 431 | 0.496 | 0.8 |
| 6 | 356 | 0.497 | 1.1 |
| 7 | 196 | 0.487 | -0.8 |
| 8 | 104 | 0.491 | -0.14 |
| 9 | 81 | 0.485 | -1.3 |
| 10 | 78 | 0.488 | -0.75 |
(ihou2:11/25の異方性1次解析のデータ ihou2ji:2次要素の異方性単純梁のデータ ihouriron2:異方性1次の理論値0.4917mm sand2ji:2次要素のサンドウィッチ梁 sandrironti:サンドウィッチ梁の理論値0.099mm)
1次要素のサンドウィッチ梁のデータ
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) |
| 0.5 | 583289 | 0.08164 | -17.5 |
| 0.6 | 214850 | 0.07724 | -22 |
| 0.7 | 155276 | 0.07681 | -22.4 |
| 0.8 | 139020 | 0.07642 | -22.8 |
| 0.9 | 83327 | 0.07678 | -22.4 |
| 1.2 | 32182 | 0.07602 | -23.2 |
| 1.3 | 28507 | 0.07652 | -22.7 |
| 1.4 | 24105 | 0.07563 | -23.6 |
| 1.5 | 19934 | 0.07602 | -23.2 |
| 1.6 | 19653 | 0.07603 | -23.2 |
| 1.8 | 12468 | 0.07620 | -23 |
| 2 | 10647 | 0.07373 | -25.5 |
| 3 | 3599 | 0.06616 | -33.2 |
| 4 | 1665 | 0.05568 | -43.8 |
| 5 | 1067 | 0.05320 | -46.2 |
| 6 | 834 | 0.03034 | -69.4 |
| 7 | 554 | 0.01788 | -81.9 |
| 8 | 289 | 0.01806 | -81.8 |
| 9 | 261 | 0.01413 | -85.7 |
| 10 | 232 | 0.03341 | -66.3 |
異方性1次単純梁と1次要素&2次要素サンドウィッチ梁の比較グラフ(sand1ji:1次要素のサンドウィッチ梁 sand2ji:2次要素のサンドウィッチ梁 sandrironti:サンドウィッチ梁の理論値0.099mm ihouriron2:異方性1次の理論値0.4917mm ihou2:11/25の異方性1次解析のデータ )
メモ:サンドウィッチ梁を1次要素に変えたらどうなるか気になったので解析してみた。(2次要素と同じ条件にするため、メッシュ長さ0.5,0.6の結果は除いてある) 2次要素のサンドウィッチ梁の解析結果を比較すると、理論値より相対誤差が大きくずれていることが分かる。(特にメッシュ長さ3以上) 11/25(金)の課題でも述べたが、2次要素の解析が1次要素より正確なのは、この結果を見ても分かるだろう。
<等方性1次のデータは11/18(金)課題を参照>
二次要素の等方性のデータ(メッシュ長さ0.5は要素数が多すぎて解析できませんでした。)
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 604167 | - | - | 千代岡 |
| 0.6 | 203209 | 0.42383 | 0.98 | 高井 |
| 0.7 | 145234 | 0.43301 | 3.22 | 関合 |
| 0.8 | 140987 | 0.43006 | 3.2 | 岡田 |
| 0.9 | 91974 | 0.429913 | 3.18 | 松田 |
| 1.2 | 24800 | 0.429777 | 3.14 | 青野 |
| 1.3 | 23132 | 0.42989 | 3.16 | 山口 |
| 1.4 | 17617 | 0.429745 | 3.13 | 山本 |
| 1.5 | 15433 | 0.429844 | 3.2 | 進藤 |
| 1.6 | 15900 | 0.429754 | 3.13 | 河合 |
| 1.8 | 11677 | 0.42962 | 3.1 | 山口 |
| 2 | 10460 | 0.429605 | 3.1 | 進藤 |
| 3 | 2486 | 0.429217 | 3.0 | 山本 |
| 4 | 1453 | 0.4293 | 3.02 | 関合 |
| 5 | 431 | 0.427885 | 2.69 | 千代岡 |
| 6 | 360 | 0.4282 | 2.78 | 高井 |
| 7 | 196 | 0.42606 | 2.25 | 青野 |
| 8 | 104 | 0.42631 | 2.3 | 岡田 |
| 9 | 81 | 0.42513 | 2.03 | 松田 |
| 10 | 78 | 0.424466 | 1.8 | 河合 |
一次と二次要素の等方性比較のグラフ(niji:二次要素のデータ rironti1118:単純梁理論値0.4167mm tanjunbari0.5nashi:要素数0.5を抜いた1次要素単純梁のデータ)
メモ:[1次要素は頂点の節点だけで要素の変形を表現する、2次要素は頂点と頂点の間に存在する節点をも用いて要素の変形を計算する→変形に対する追随性が高く精度の高い結果が得られる。 (引用元:日経XTECH 第2回精度はメッシュで決まる https://xtech.nikkei.com/dm/article/FEATURE/20111012/199212/?P=3#:~:text=%E6%AC%A1%E6%95%B0%E3%81%A8%E3%81%AF%EF%BC%8C%E8%A6%81%E7%B4%A0%E5%BD%A2%E7%8A%B6,%E3%82%92%E6%8C%81%E3%81%A4%EF%BC%88%E5%9B%B36%EF%BC%89%E3%80%82)]
↑2次要素の解析での相対誤差が1次要素より小さいのは恐らくこれが理由だと思われる。
グラフを見ると、1次要素よりも理論値に近い解析ができており、値としては、0.43±0.005の範囲内に落ち着いている。しかし、要素数が大きすぎると1次要素より解析に時間がかかることor解析できないことがあることが分かった。これは、[ ]に書いた2次要素の定義から考えると、1次要素よりも多くの節点を用いて変形の計算を行なっているので、要素数が多いほどパソコンにかかる負荷が1次要素より大きいからだと思われる。 実際、メッシュ長さ0.5の解析はできなかった。(他のパソコンでも解析したが、解析できなかった。)
異方性1次のデータ(メッシュ長さ1.0と1.1追加)
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 604167 | 0.50919 | 3.56 | 千代岡 |
| 0.6 | 203209 | 0.50472 | 2.6 | 高井 |
| 0.7 | 145234 | 0.5036 | 2.42 | 関合 |
| 0.8 | 140987 | 0.50283 | 2.3 | 岡田 |
| 0.9 | 91974 | 0.50053 | 1.8 | 松田 |
| 1.0 | 77582 | 0.4999 | 1.6 | 千代岡 |
| 1.1 | 27533 | 0.4886 | -0.63 | 千代岡 |
| 1.2 | 24800 | 0.48739 | -0.9 | 青野 |
| 1.3 | 23132 | 0.48841 | -0.67 | 山口 |
| 1.4 | 17617 | 0.48403 | -1.56 | 山本 |
| 1.5 | 15433 | 0.48202 | -2.0 | 進藤 |
| 1.6 | 15900 | 0.48329 | -1.7 | 河合 |
| 1.8 | 11677 | 0.47855 | -2.67 | 山口 |
| 2 | 10460 | 0.47906 | -2.6 | 進藤 |
| 3 | 2436 | 0.42787 | -12.98 | 山本 |
| 4 | 1453 | 0.42772 | -13.02 | 関合 |
| 5 | 431 | 0.27364 | -44.3 | 千代岡 |
| 6 | 360 | 0.33927 | -31.0 | 高井 |
| 7 | 196 | 0.21363 | -58.5 | 青野 |
| 8 | 104 | 0.22574 | -54.1 | 岡田 |
| 9 | 81 | 0.22750 | -53.7 | 松田 |
| 10 | 78 | 0.20327 | -58.7 | 河合 |
等方性1次と異方性1次の比較のグラフ(ihou:異方性1次のデータ ihourironti:異方性理論値0.4917mm rironti1118:単純梁理論値0.4167mm tanjunbari:11/18の単純梁解析のデータ )
メモ:解析結果から異方性1次単純梁の変位は約0.50mmに落ち着くと判断した。また、このグラフも異方性の理論値と交わる点があるので相対誤差0に近いメッシュ長さを探すのも面白いかも。<1/16(月)追記 メッシュ長さ1.0,1.1についても解析してみたが、その間に相対誤差0のメッシュ長さが存在する。今回、解析した範囲ではメッシュ長さ1.1で解析するとより正確だと思われる。>
後、等方性1次のグラフと比較すると、お互いグラフの形が似ているが、これは等方性1次単純梁の理論式\( \delta = \frac{P\ell^3}{3EI} \)に\( \delta = \frac{P\ell}{kGA} \)を加えたものが異方性1次単純梁の理論式であるので、等方性1次のグラフに\( \delta = \frac{P\ell}{kGA} \)を加えたら異方性1次のグラフになるはずだからである。(グラフより、多少のずれがあるので実際はそのままの形で移動していない。)
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 604167 | 0.428982 | 2.94 | 千代岡 |
| 0.6 | 361584 | 0.421233 | 1.09 | 高井 |
| 0.7 | 145234 | 0.4225 | 1.4 | 関合 |
| 0.8 | 140987 | 0.422627385 | 1.4 | 岡田 |
| 0.9 | 91857 | 0.420351606 | 0.88 | 松田 |
| 1.0 | 77582 | 0.4192 | 0.6 | 千代岡 |
| 1.1 | 27533 | 0.4057 | -2.6 | 千代岡 |
| 1.2 | 24520 | 0.404744325 | -2.87 | 青野 |
| 1.3 | 23132 | 0.4045 | -2.93 | 山口 |
| 1.4 | 17530 | 0.3986 | -4.34 | 山本 |
| 1.5 | 15433 | 0.396317756757 | -4.9 | 進藤 |
| 1.6 | 15900 | 0.399049 | -4.24 | 河合 |
| 1.8 | 11677 | 0.404457 | -2.94 | 山口 |
| 2 | 10460 | 0.394818715517 | -5.3 | 進藤 |
| 3 | 2344 | 0.32447 | -22.13 | 山本 |
| 4 | 1453 | 0.3329 | -20.1 | 関合 |
| 5 | 431 | 0.136240 | -67.3 | 千代岡 |
| 6 | 360 | 0.2130486 | -48.9 | 高井 |
| 7 | 196 | 0.1019892 | -75.5 | 青野 |
| 8 | 104 | 0.1158624 | -72.2 | 岡田 |
| 9 | 81 | 0.1247076 | -70.1 | 松田 |
| 10 | 78 | 0.07733 | -81.4 | 河合 |
単純梁のグラフ:縦軸 変位(mm) 横軸 要素数 (rironti1118:単純梁理論値0.4167mm tanjunbari:単純梁のデータ)
メモ:解析結果から、単純梁のグラフの傾きが0に近づくのは約0.42mmだと判断した。また、メッシュ長さ0.9〜1.2の間で理論値と交わる点が存在するはずなので、その間で解析するとかなり精度の高い解析ができると思われる。(次は相対誤差0に近いメッシュサイズを探してみる→1/16(月)追記 メッシュ長さ1.0,1.1についても解析してみたが、その間に相対誤差0のメッシュ長さが存在する。今回、解析した範囲ではメッシュ長さ1.0で解析すると相対誤差0に近い状態で変位が出るので、メッシュ長さ1.0で解析するのがベストだと思われる。)
| メッシュ長さ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 59504 | 6.56 | -1.5 | 千代岡 |
| 0.6 | 45512 | 6.48774 | -2.69 | 高井 |
| 0.7 | 39075 | 6.54133 | -2.0 | 関合 |
| 0.8 | 13397 | 6.43695 | -3.5 | 岡田 |
| 0.9 | 9903 | 6.36315 | -4.6 | 松田 |
| 1.2 | 6256 | 6.3043375 | -5.4 | 青野 |
| 1.3 | 5767 | 6.29784 | -5.6 | 山口 |
| 1.4 | 5146 | 6.286015 | -5.76 | 山本 |
| 1.5 | 3935 | 6.24807 | -6.3 | 進藤 |
| 1.6 | 3400 | 6.20446 | -6.98 | 河合 |
| 1.8 | 2952 | 6.17161 | -7.5 | 山口 |
| 2 | 1632 | 5.64585 | -15.3 | 進藤 |
| 3 | 667 | 5.4053975 | -18.96 | 山本 |
| 4 | 264 | 3.6161 | -45.8 | 関合 |
| 5 | 191 | 3.86 | -42 | 千代岡 |
| 6 | 190 | 2.5077325 | -62.4 | 高井 |
| 7 | 75 | 1.41225 | -78.8 | 青野 |
| 8 | 56 | 1.2887175 | -80.7 | 岡田 |
| 9 | 49 | 1.28799 | -80.9 | 松田 |
| 10 | 44 | 1.226075 | -81.6 | 河合 |
片持ち梁のグラフ:縦軸 変位(mm) 横軸 要素数 (katamochi:片持梁のデータ rironti:片持梁の理論値6.67mm)
メモ:解析結果から、片持ち梁のグラフの傾きが0に近づくのは先端変位6.5±0.1mmのときだと読み取れる。また、要素数が大きいほど相対誤差が小さいことから、正確な解析ができることが分かった。(その分、History Viewでの解析時間も長くなるが...。)
・課題で作成したグラフ
2月10日(金)
今日で発表含め創造工房実習の課題が全て終わりました。ただ、質問に対して答えることができなかったので、春休み課題の発表ではしっかり答えられるように知識をつけたいです。 次は春休み課題(弾塑性解析)を行う必要があるので、それに向けて頑張ります。
1/31(火)
今日は中村先生の講義に参加しました。 特に印象に残ったのは、ケーブルに乾燥した空気を送りこんで腐食の対策をしていることでした。明石海峡大橋は四国に行く際によく使っていたので、ケーブルにこういった対策をしていることに非常に驚きました。 ケーブルに関する知識は鋼橋の研究をする際に必要になる知識なので、メモしたものは綺麗にまとめて忘れないようにします。
1/11(水)
今日の創造工房実習でLaTeXについて一通り学びました。 後は課題提出に向けて作業するのみなので、頑張っていきたいと思います。
1/9(月)
遅くなりましたが、2023年が始まりました。今年もよろしくおねがいします。 明後日、創造工房実習があるので、LaTeXについて昨年学んだことを確認するために復習を行いました。 また、創造工房実習の課題の締切まであと約1ヶ月後なので、計画的に進めていきたいと思います。
12/16(金)
LaTeXについて学びました。色々覚えることはありそうですが、ゆっくり覚えていこうと思います。後、英語もう少し勉強します...。
12/14(水)
これまで行なってきた解析データやグラフを少し整理しました。これからまとめ作業に入るみたいなので、できるだけ進めやすいように整理していきます。
12/9(金)
本日は中村先生の特別講義を聴講しました。東京湾アクアラインなどの有名な橋の設計をされた方で、振動解析などのお話を聞くことができました。 明石海峡大橋のお話は別の機会でしてくださるそうなので、次にお話する機会が来る日までに自分の知識を高めようと思います。
12/8(木)
12/2の課題を終わらせました。明日は特別講義ですが、どんな話を聞けるのか楽しみです。(質問される?みたいなので、橋について復習しておいたほうがいいかも...。)
12/5(月)
salome-mecaの単純梁の復習とサンドウィッチ梁の1次要素解析を行なってみました。(グラフは後日作成) 2次要素の結果はまだ出ていませんが、結果がでた後に1次とどう違うのか見比べてみます。
12/3(土)
salome-mecaで行う片持梁解析の復習を行いました。恐らく、来年は自分たちが次の後輩たちに教えることになると思うので、今時間があるうちに教わったことを復習+まとめておきたいと考えています。(今一番にやることはそれかな...。)
12/2(金)
本日で創造工房で習うsalome-mecaの演習が終わりました。今までやったことを忘れないように復習は忘れずに行いたいと思います。
12/1(木)
11/25の課題を終わらせました。明日はサンドウィッチ梁の解析を行うので、資料を一通り見ておこうと思います。 今年も残り1か月です。(月初めから大雪でしたが...(-_-;))
2022年の残りの期間も楽しく過ごしつつ、自分の知識を高めていきたいと思います。
2022年11月の記録 [#o8b95629]
11/28(月)
2次要素メッシュ長さ0.5の解析を違うパソコンを使って行いましたが、要素数が多すぎて解析できませんでした。メッシュ長さ0.5を抜いて、結果をまとめようと思います。
11/25(金)
今日も先週に引き続きsalome解析を学びました。ただ、2次要素でのノード0.5の要素数が多すぎて、エラーを起こすので自分の使っているパソコンでは解析不可という状況です。対応策は教えてもらったので、まだどうなるか分かりませんが、やれることは全てやっておきたいと思います。 また、今週は研究室で色々な方からお話を聴きました。中には貴重な話や裏話もあって面白かったので、人との関わりは大事だなと思いました。同時に、自分も色々な話ができるように知識やネタを増やしていきたいとも思いました。(約1年後には後輩も入ってきますし...。)
11/18(金)
salomeで単純梁の解析について学びました。やることは単純梁の解析と似ているので、前回の復習にもなりましたが、思っていたより忘れていたことが多かったです...。
11/11(金)
salomeについて学びました。次回もsalomeを使った解析を行うので、今日学んだことを忘れないように復習します。
11/9(水)
viiとgnuplotの使い方を軽く復習しました。
11/4(金)
初めて昼休憩での英語会話に参加しましたが、皆さんの会話を聴いて理解するのに精一杯でした。 理解して自分の考えを英語で話すことができるように英語力を鍛えていきたいです。
また、本日の創造工房でgnuplotとviについて学びました。 今後、salomeなど様々なことを学びますが、これらの機能を使えるようになって効率よく作業できるようになることを目指します。
11/2(水)
UNIXコマンドを実際に使ってみました。昨日調べたものを含め色々試してみましたが、便利なものもあれば、どこで使うんだろうと思うコマンドもありました。 これから様々な場面でUNIXコマンドを使う機会があるはずなので、授業等で使いながら覚えていこうと思います。
(ちなみに...ctrl+zで実行しているコマンドを終了させることができるみたいです。使う機会はありそうなので、覚えておこうと思います。) 11/4追記:ctrl+zはどうやらコマンドの強制終了らしいので、あまり使わないほうがいいかも...。
11/1(火)
UNIXコマンドについて調べました。使えそうなコマンドをいくつか見つけたので、明日試してみようと思います。
<取り組むこと>
・UNIXコマンドについて学ぶ。
・構造・材料系の本を読む
2022年10月の記録 [#z5e925c3]
10/28(金)
UNIXコマンドについて学びました。資料に載っているコマンド以外にも色々なコマンドがあるとのことなので、自分で調べてみて、使えるコマンドを増やしていきたいと思います。
10/27(木)
タッチタイプの一通りの流れをストップウォッチで計測したら、2分59秒でした。 しかし、キーボードを見ながらの記録なので、できる限り、下を見ないように打てるようになりたいです。
(追記)木材についての勉強を始めました。(本:プロでも意外に知らない<木の知識> 林 知行 著)
10/24(月)
タッチタイプの練習を行いました。大文字と小文字を交互に打つところ(aBc,Abcなど)で時間がかかってしまうので、そこをできるだけもたつかずに打てるようにしたいです。
10/21(金)
タッチタイプの練習を行いました。まずは、3分以内に打つことを目標にします。
<取り組むこと>
・タッチタイプの練習
・構造・材料系の本を読む