回転座標

振動解析における回転系座標についての検証を行う。

片持ち梁†

X=100,Y=10,Z=20の片持ち梁を作成。画像奥側が固定面。

等方性†

細かい条件については、根本の卒論日誌：片持ち梁の振動解析（ソリッド要素）と同じ。

異方性†

等方性から、材料条件のみを変更。

ihou = DEFI_MATERIAU(
 ELAS_ORTH=_F(
   E_L=6000.0, 
   E_N=240.0, 
   E_T=240.0, 
   G_LN=400.0, 
   G_LT=400.0, 
   G_TN=400.0, 
   NU_LN=0.016, 
   NU_LT=0.016, 
   NU_TN=0.016, 
   RHO=3.8e-07
 )

異方性+回転+回転座標適用†

梁を回転させて、かつ回転座標を適用させる。

材料設定について、上のELAS_ORTHをそのまま適用。

回転座標については

AFFE_CARA_ELEM > MASSIF > ANGL_REP
入力欄を3つ作成し、それぞれがX,Y,Zに対応している。
それぞれの軸回りでいくら回転させるかを入力。
ex)今回の場合、Y軸を90度回転させるので、1番目に0、2番目に90、3番目に0を入力

回転座標を適用する前と同じ結果になったため、ANGL_REPで回転座標を適用できるといえる。

結果†

片持ち梁の場合は、ANGL_REPでの回転座標適用は有効だと考えられる。

単純梁†

次に、同じくX=100,Y=10,Z=20で単純梁を作成。

固定方法については、Salome-Meca演習_単純梁のジオメトリの作成と同じ。

等方性†

材料設定は片持ち梁と同じ。

固定箇所が回転しているように見えるが、確認したところ回転していなかった。

異方性†

材料設定は片持ち梁と同じ。

異方性+回転+回転座標適用†

片持ち梁と同様に梁を回転させ、ANGL_REPを適用させる。

回転前と少しだけ振動数が違う。

ANGL_REPが正しく適用されていない可能性もあるため、比較用に回転前の梁（X軸方向が長軸）に回転座標を適用させてみる。

【比較用】異方性+回転座標で梁を回転させなかった場合†

異方性を持たせて回転なしのときと、異方性+回転+回転座標適用のときとも違う結果になったため、 これを見る限り、回転座標は適用されているようだ。

結果†

単純梁の場合は、ANGL_REPでの回転座標適用は有効だと考えられるが、 回転前と後で少しだけ振動数が違った。

考えられる原因としては、単純梁は線要素での固定であるため、片持ち梁のような面要素での固定よりも 固定部分の周りが動きやすいことから、

その違いが振動数となって現れた可能性は考えられる。

アーチ†

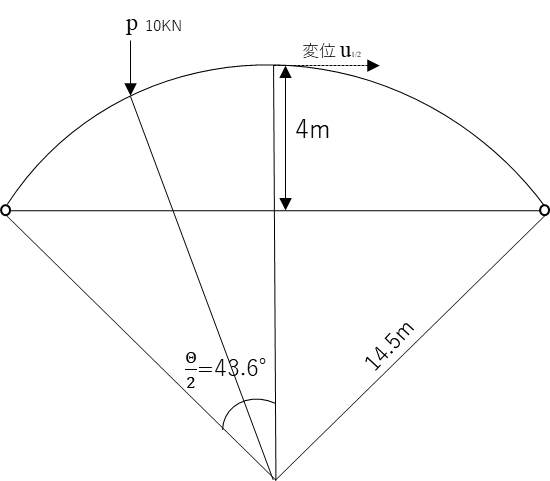
アーチへの適用も検証する。 図の3点を使用してアーチを作成。

等方性†

材料設定は以下のとおり。

mater = DEFI_MATERIAU(
 ELAS=_F(
   E=7500.0, 
   NU=0.4, 
   RHO=3.8e-10
 )

【比較用】異方性†

異方性アーチの場合はELAS_ISTRを使用するのがいいらしい。（及川さん談）

ihou = DEFI_MATERIAU(
 ELAS_ISTR=_F(
   E_L=7500.0, 
   E_N=300.0, 
   G_LN=400.0, 
   NU_LN=0.016, 
   NU_LT=0.016, 
   RHO=3.8e-10
 )

アーチの場合下記の回転座標適用をしないと、ただの直交異方性が適用されてしまうので、参考値とする。

異方性+回転座標適用†

アーチの回転座標適用にはANGL_AXEとORIG_AXEコマンドを使用する。 （上のANGL_REPと同じ位置にある）

ANGL_AXEは回転角（図を参照）、ORIG_AXEはアーチの中心座標を指定する。

elemprop = AFFE_CARA_ELEM(identifier='2:1',
                         MASSIF=_F(ANGL_AXE=(0.0, 90.0),
                                   GROUP_MA=('Cut_1', ),
                                   ORIG_AXE=(0.0, 10000.0, 14500.0)),
                         MODELE=model)

上の異方性のみの材料設定よりも、固定端近くの剛性が高いように見える。

【比較用】回転座標の適用について†

ORIG_AXEでアーチの中心座標を指定するが、ANGL_AXEで回転角を調整する前の中心座標か調整後の中心座標かわからなかったので、検証用として回転角を調整前の中心座標（X=14500,Z=0）を入力して解析する。

elemprop = AFFE_CARA_ELEM(identifier='2:1',
                         MASSIF=_F(ANGL_AXE=(0.0, 90.0),
                                   GROUP_MA=('Cut_1', ),
                                   ORIG_AXE=(14500.0, 10000.0, 0.0)),
                         MODELE=model)

他の結果よりも梁が横に伸びたように見える。

ELAS_ORTHを使用した場合†

ihou2 = DEFI_MATERIAU(identifier='5:1',
                     ELAS_ORTH=_F(E_L=7500.0,
                                  E_N=300.0,
                                  E_T=300.0,
                                  G_LN=400.0,
                                  G_LT=400.0,
                                  G_TN=400.0,
                                  NU_LN=0.016,
                                  NU_LT=0.016,
                                  NU_TN=0.016,
                                  RHO=3.8e-10))

ELAS_ISTRと全く違う値になった。 回転座標は適用させているので、及川さんのアーチ橋に異方性を適用させたら振動数が変わったのはこれが原因かも？

まとめ†

等方性と異方性について比較すると、異方性の方が小さい値の振動数になる傾向があることがわかった。

また、アーチの異方性については、ELAS_ISTRを使用し、ANGL_AXEで回転角を、ORIG_AXEで回転の原点を指定する。

11/22追記†

code_asterマニュアル「Operator DEFI_MATERIAU」P21に、以下の記載がある。

3.6 Keywords factor ELAS_ISTR, ELAS_ISTR_FO, ELAS_VISCO_ISTR
Definition of the constant elastic characteristics (ELAS_ISTR) or functions of the temperature in the
case of the transverse isotropy for the isoparametric solid elements (ELAS_ISTR_FO). It is possible to
define   constant   transverse   isotropic   characteristics   viscoelastic   (ELAS_VISCO_ISTR)  at  a  given
frequency, the modules to be informed are then complex.
By taking again the same notations as for the orthotropism, the transverse isotropy means here that
isotropy is in the plan  (L,T)  and that the orthotropism is thus carried by the direction  N  [R4.01.02].
One can draw the attention of  the reader to the fact that this convention differs from  a usual
convention   which   indicates   by   “longitudinal   direction”   the   direction   of   orthotropism   of   isotropic
transverse materials.

• isotropy is in the plan (L,T) and that the orthotropism is thus carried by the direction N より、ELAS_ISTRの場合、LTは等方性を持つことから、Nが繊維方向の強さになり、LTは繊維直角方向の強さを当てはめる。

• ELAS_ISTRを以下のように書き換え、再度解析をする。

  ihou3 = DEFI_MATERIAU(
   ELAS_ISTR=_F(
     E_L=300.0, 
     E_N=7500.0, 
     G_LN=400.0, 
     NU_LN=0.016, 
     NU_LT=0.016, 
     RHO=3.8e-10
   )

異方性のみ(回転なし)†

異方性+回転座標†

上の結果にANGL_AXEとORIG_AXEを適用させる。 おそらくこれが正しい（マニュアル上は）アーチへの異方性の適用のさせ方。

【比較用】異方性(ELAS_ORTH)+回転座標†

比較用に、ELAS_ORTHについても修正したものを使用して解析する。

ihou4 = DEFI_MATERIAU(
 ELAS_ORTH=_F(
   E_L=300.0, 
   E_N=7500.0, 
   E_T=300.0, 
   G_LN=400.0, 
   G_LT=400.0, 
   G_TN=400.0, 
   NU_LN=0.016, 
   NU_LT=0.016, 
   NU_TN=0.016, 
   RHO=3.8e-10
 )

まとめ†

以下に等方性アーチの結果と、（マニュアル上はおそらく正しい）異方性アーチの結果についてまとめる。

• 等方性

  mater = DEFI_MATERIAU(
   ELAS=_F(
     E=7500.0, 
     NU=0.4, 
     RHO=3.8e-10
   )

• 異方性

  elemprop = AFFE_CARA_ELEM(identifier='2:1',
                           MASSIF=_F(ANGL_AXE=(0.0, 90.0),
                                     GROUP_MA=('Cut_1', ),
                                     ORIG_AXE=(0.0, 10000.0, 14500.0)),
                           MODELE=model)
  ihou3 = DEFI_MATERIAU(
   ELAS_ISTR=_F(
     E_L=300.0, 
     E_N=7500.0, 
     G_LN=400.0, 
     NU_LN=0.016, 
     NU_LT=0.016, 
     RHO=3.8e-10
   )

比較すると、全体的に1/3程度の振動数になっている。

斜めの梁†

(10,10,100)でジオメトリを作成後、Y軸を軸として45°回転させる。

これを片持ち梁として解析→伸びを手計算と比較し、グローバル座標系/ローカル座標系について考察を行う。

解析†

• 解析条件

  E=7500
  NU=0.4
  荷重は、FX=FZ=1.414213562(梁の長手方向に100Nになる)

  

DX変位†

DY変位†

ほとんど変化はない。

DZ変位†

計算結果との比較†

解析値の合力は\( \frac{DX+DZ}{2}×\frac{1}{\sqrt{2}} \)で計算。

理論値と解析値の相対誤差はかなり小さいため、解析自体に問題はないと思われるが、変位、各種応力についてはX,Y,Z座標ごとにしか表示させることはできなかった。

【比較用】斜めじゃない梁†

斜めにしない（Z軸に並行な）梁について比較する。条件は同じ。

ひずみ、応力の比較†

ひずみ、応力についても比較する。

同じ結果ではないため、斜めの梁でも並行な梁でも同じ座標系が適用されているわけではないようだ。

ANGL_REPとANGL_EULER†

ANGL_REPとANGL_EULERの場合でY軸を軸に45°回転を適用させて、座標系が変化しているか見る。

①elemprop = AFFE_CARA_ELEM(identifier='2:1',
                         MASSIF=_F(ANGL_REP=(0.0, 45.0, 0.0),
                                   GROUP_MA=('naname', )),
                         MODELE=model)

②elemprop = AFFE_CARA_ELEM(identifier='2:1',
                         MASSIF=_F(ANGL_EULER=(0.0, 45.0, 0.0),
                                   GROUP_MA=('naname', )),
                         MODELE=model)

①と②と上の結果を比較する。

変化がないので、座標系の適用方法が間違っているかもしれない。

メモ†

salomeメモの「局所座標系」(近藤さん編集？)を確認すると、以下の記載がある。

                    MASSIF=(_F(GROUP_MA='moto',               ←回転なしの梁に適用
                                ANGL_EULER=(0.0,0.0,0.0,),     #(\psi,\theta,\phi)
                                ),
                             _F(GROUP_MA='alp330',　　　　　　 ←θx=330°傾けた梁に適用
                                ANGL_EULER=(0.0,330.0,270.0,), #(\psi,\theta,\phi)
                                ),
                             _F(GROUP_MA='bt30',               ←θy=30°傾けた梁に適用
                                ANGL_EULER=(90.0,30.0,270.0,), #(\psi,\theta,\phi)
                                ),
                             ),
                     );

270.0の数字がよくわからない。

3つ目の数字はθzの回転？ だとしたら、オイラー角の適用のさせ方か考え方が間違っている可能性があるかも。

'21.12.02 近藤より†

ここでは，\( E_{xx}=E_{yy}=\frac{E_{zz}}{25} \)としているので，\( \phi \)の値は何であっても結果は変わらないと思いますが，より一般化するために後藤さんの軸のとり方に合わせて載荷方向がy軸の正となるように回転させました（うろ覚え）． ちなみにANGL_EULERは若干ややこしい（下記）ので，このようなサイトでチェックするのがいいかもです．

• (X, Y, Z) → \( \psi \):Z軸右回り → (x1, y1, z1)
• (x1, y1, z1) → \( \theta \):x1軸右回り → (x2, y2, z2)
• (x2, y2, z2) → \( \phi \):z2軸右回り → (x3, y3, z3)

追記†

まさかの近藤さんからコメントが・・・ありがとうございます。

もう一度マニュアルについて確認したところ、近藤さんのコメントの通りZ→X→Z'の順番の回転でした。 （ずっとオイラー角はx→y→zの順だと思ってました）

ななめの梁を異方性にして等方性と比較†

まず、オイラー角の設定を以下に修正。

elemprop = AFFE_CARA_ELEM(identifier='2:1',
                         MASSIF=_F(ANGL_EULER=(90.0, 45.0, 0.0),
                                   GROUP_MA=('naname', )),
                         MODELE=model)

これで斜めの梁の中心にZ軸が通る（はず）

材料設定を2種類作る。

mater = DEFI_MATERIAU(identifier='3:1',
                     ELAS=_F(E=7500.0,  #等方性
                             NU=0.4))
mater = DEFI_MATERIAU(identifier='3:1',
                     ELAS_ORTH=_F(E_L=300.0, #異方性
                                  E_N=7500.0,
                                  E_T=300.0,
                                  G_LN=400.0,
                                  G_LT=400.0,
                                  G_TN=400.0,
                                  NU_LN=0.016,
                                  NU_LT=0.016,
                                  NU_TN=0.016))

E_Nを7500にして、ANGL_EULERの設定が正しければ材料の強軸方向ヤング率が等方性と異方性で同じなので、先端の変位、応力はほぼ同じになるはず。

等方性、異方性でほぼ同じ結果が出たため、正しく適用できたようだ。

気になること†

• LIAISON_OBLIQUEで局所座標をノードに適用させることができる？という情報があるが細かい適用方法がよくわからない
• LIAISON_OBLIQUEは固定面と同じ面のノードで設定するとエラーになる
• Paravisのオブジェクトインスペクターの「GenerateVectors」の使用方法（unnamed_○○_Vectorというのが追加される）

アーチ（変形）†

アーチの異方性をsalome_meca2019のAFFE_CARA_ELEM > MASSIF > ANGL_AXEを用いて 回転対称性、横方向等方性の軸指定でやってみる。

• 
• ANGL_AXEの設定は以下

  elemprop = AFFE_CARA_ELEM(
   MASSIF=_F(
     ANGL_AXE=(0.0, 90.0), 
     GROUP_MA=('Cut_1', ), 
     ORIG_AXE=(0.0, 10000.0, 14500.0)
   ), 
   MODELE=model
  ) 

• ANGL_AXEは回転対称軸の角度　(0,90)で(L,T,N)=(Z,Y,-X)になる
• ORIG_AXEは回転対称の中心　今回の場合アーチの円弧の中心(0,10000,14500)

  等方性（E=7500）	等方性（E=300）	異方性（EL=7500 EN=300）
  2.505	62.618	6.156

• 振動解析（等方性E=7500） ここ
• 振動解析（等方性E=300）

  振動モード	解析値(Hz)
  水平一次	0.8344
  鉛直二次	1.8885
  水平二次	2.3257
  対称一次	4.1671
  水平三次	4.6612
  対称二次	7.6607
  水平四次	7.9425
  鉛直四次	8.3786
  水平五次	12.0524
  対称三次	13.0186

• 振動解析（異方性EL=7500,EN=300） ここ

local axis†

• https://code-aster.org/UPLOAD/DOC/Formations/06-structural-elementsce-2.pdf
• ↑を見ると、paravis上でlocal axisを表示させている。
• もしかしたら、結果の出力（CREA_CHAMP）とかで表示させることができるコマンドがあるのかも。

最新の100件