- 卒論日誌
- かじか橋アーチ部分における腐朽を考慮した振動解析
- ソリッド要素と梁要素の振動解析精度の比較(アーチ、片持ちばり)
- 梁の振動解析
- 単純梁の振動解析(シェル要素)(x,y,z)=(600,50,0)
- 片持ち梁の振動解析(シェル要素)(x,y,z)=(100,10,0)
- 片持ち梁の振動解析(梁要素)(x,y,z)=(100,0,0)
- 片持ち梁の振動解析(ソリッド要素)(x,y,z)=(100,10,20)
- 片持ち梁の振動解析(ソリッド要素)(x,y,z)=(100,10,10)
- 作業日誌(5月)
- 材料非線形解析(弾塑性)
- 3年次
卒論日誌†
振動解析を用いた木橋の劣化状態の予測 [#d29acbab]
今後の課題(引き継ぎ)†
- 床版以外の部材(特にアーチ)の異方性の適用.
- 固有振動数に対する影響が大きかったアーチ支柱接合部の劣化範囲拡大(特に支柱部分).
- 劣化具合,劣化箇所を増やす.
fieldmatの個数制限†
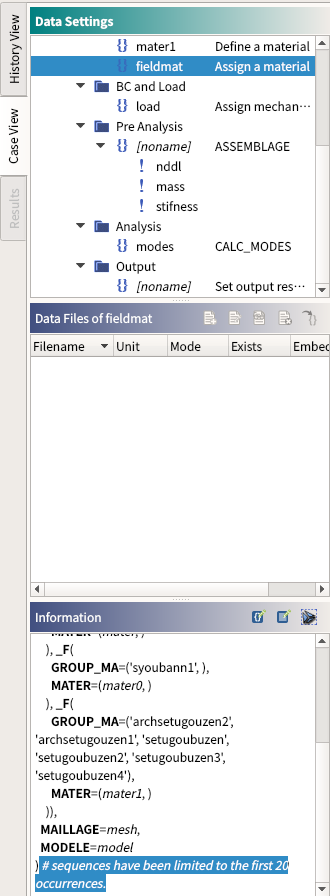
- fieldmatのMaterial assignementの数とGroup of elementの中の個数が20個までに制限されている.
実測との比較†
- 32年経過のかじか橋2019年調査から得られた測定値に近づけ,推定ヤング率を算出する.
- より解析精度を上げるために,要素数を100万程度(2次メッシュ)に設定する.
- 支点部・継手部の腐朽劣化とそれ以外の箇所(健全部分)を段階的にヤング率を減少させる.
解析結果†
- ヤング率E
健全:980000[tf/m^2]
腐朽:980[tf/m^2]
欠損:70[tf/m^2]
- ポアソン比 ν=0.4 密度 ρ=0.0459[tf/m3]
| 振動モード | 測定値 | 全て健全[Hz] | 部分的腐朽劣化(支点部・継手部)[Hz] | 全体ヤング率3割減少[Hz] | 全体ヤング率5割減少[Hz] | 全体ヤング率6割減少[Hz] | 全体ヤング率7割減少[Hz] |
| 水平一次 | 2.37 | 12.3006 | 10.8957 | 9.11776 | 7.70708 | 6.89407 | 5.97117 |
| 鉛直逆対称一次 | 8.69 | 17.6497 | 14.2401 | 11.9164 | 10.0733 | 9.01131 | 7.80603 |
| ねじれ | | 18.9542 | 15.4512 | 12.9327 | 10.9337 | 9.78135 | 8.47317 |
| 鉛直1次 | 15.38 | 21.23 | 18.3786 | 15.3814 | 13.0041 | 11.6343 | 10.0797 |
| ねじれ | | 23.2348 | 20.4232 | 17.0919 | 14.4491 | 12.9263 | 11.1978 |
全体ヤング率が62.8%減少したとき実験値と解析値が一致し,その時の設定ヤング率(=推定ヤング率)は主構部分が3.57GPa,床版が3.83GPaという結果になった.†
縦桁・枕梁[欠損腐朽]†
解析結果†
- ヤング率E
健全:980000[tf/m^2]
腐朽:980[tf/m^2]
欠損:70[tf/m^2]
腐朽(下流側):490000[tf/m^2]
- ポアソン比 ν=0.4 密度 ρ=0.0459[tf/m3]
- 縦桁と枕梁の接合部における欠損腐朽場所を2パターンに分けて,それぞれの固有振動数における影響度を比較する.
パターン1:縦桁と枕梁の接合部全て欠損腐朽
パターン2:縦桁と枕梁の接合部における欠損腐朽具合を上流側と下流側とで区別(上流側の欠損腐朽を大,下流側を小)
- 要素数は一次メッシュの30万程度
- 欠損腐朽場所として,縦桁は外側を欠損,枕梁は縦桁と接してる箇所を欠損腐朽
- 括弧内は「全て健全」に対する各パターンの相対誤差
| 振動モード | 全て健全[Hz] | パターン1[Hz] | パターン2[Hz] |
| 水平一次 | 13.9987 | 13.896(-0.74%) | 13.9902(-0.059%) |
| 鉛直逆対称一次 | 20.8479 | 20.64(-1.0%) | 20.7782(-0.33%) |
| 鉛直一次 | 24.8321 | 24.4318(-1.6%) | 24.4327(-1.6%) |
| ねじれ | 28.1637 | 28.7497 | 28.8119 |
| ねじれ | 30.621 | 30.2455 | 30.2735 |
| 鉛直二次 | 35.0597 | 34.4265(-1.8%) | 34.5181(-1.5%) |
モデル化†

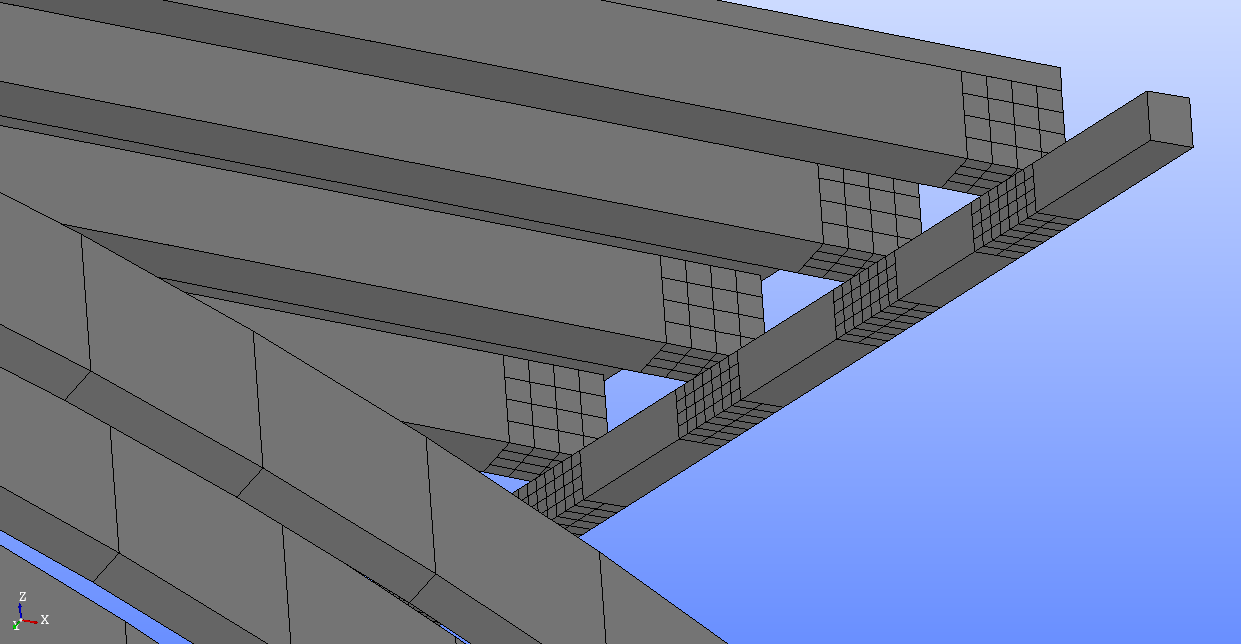
アーチ[欠損腐朽]†
解析結果†
- ヤング率E
健全:980000[tf/m^2]
腐朽:980[tf/m^2]
欠損:70[tf/m^2]
- ポアソン比 ν=0.4 密度 ρ=0.0459[tf/m3]
- アーチの欠損腐朽場所を3パターンに分けて,それぞれの固有振動数における影響度を比較する.
パターン1:アーチ端部のみ
パターン2:支柱接合部付近のみ
パターン3:中央接合部付近のみ
パターン4:アーチ端部と支柱接合部付近
パターン5:アーチ端部と中央接合部付近
パターン6:支柱接合部と中央接合部付近
パターン7:アーチ端部,支柱接合部,中央接合部付近
- 要素数は一次メッシュの30万程度
- 括弧内は「全て健全」に対する各パターンの相対誤差
| 振動モード | 全て健全[Hz] | パターン1[Hz] | パターン2[Hz] | パターン3[Hz] | パターン4[Hz] | パターン5[Hz] | パターン6[Hz] | パターン7[Hz] |
| 水平一次 | 13.9987 | 13.7703(-1.6%) | 13.4892(-3.6%) | 13.7614(-1.7%) | 13.446(-3.9%) | 13.7241(-2.0%) | 13.4449(-4.0%) | 13.4026(-4.3%) |
| 鉛直逆対称一次 | 20.8479 | 20.5437(-1.5%) | 17.8754(-14.3%) | 20.5053(-1.6%) | 17.8004(-14.6%) | 20.3643(-2.3%) | 17.6278(-15.4%) | 17.5582(-15.8%) |
| 鉛直一次 | 24.8321 | 23.9116(-3.7%) | 23.405(-5.7%) | 22.8186(-8.1%) | 22.7379(-8.4%) | 22.2347(-10.5%) | 21.7183(-12.5%) | 21.2168(-14.6%) |
| ねじれ | 28.1637 | 27.2662 | 25.6766 | 26.9552 | 25.4799 | 26.7336 | 25.137 | 24.9687 |
| ねじれ | 30.621 | 29.4339 | 28.1702 | 29.7901 | 27.508 | 29.0787 | 27.8604 | 27.235 |
| 鉛直二次 | 35.0597 | 34.269(-2.3%) | 31.1073(-11.3%) | 33.6118(-4.1%) | 30.7907(-12.2%) | 33.0724(-5.7%) | 30.0695(-14.2%) | 29.6676(-15.4%) |
鉛直逆対称一次において,パターン7>パターン6>パターン4>パターン2>パターン5>パターン3>パターン1の順で健全時に対する相対誤差が見られた.
支柱接合部付近の欠損腐朽が固有振動数に大きく影響を及ぼす可能性が高い.
鉛直逆対称一次モード:http://www.str.ce.akita-u.ac.jp/~gotouhan/j2020/nemoto/kazikaanime.ogv
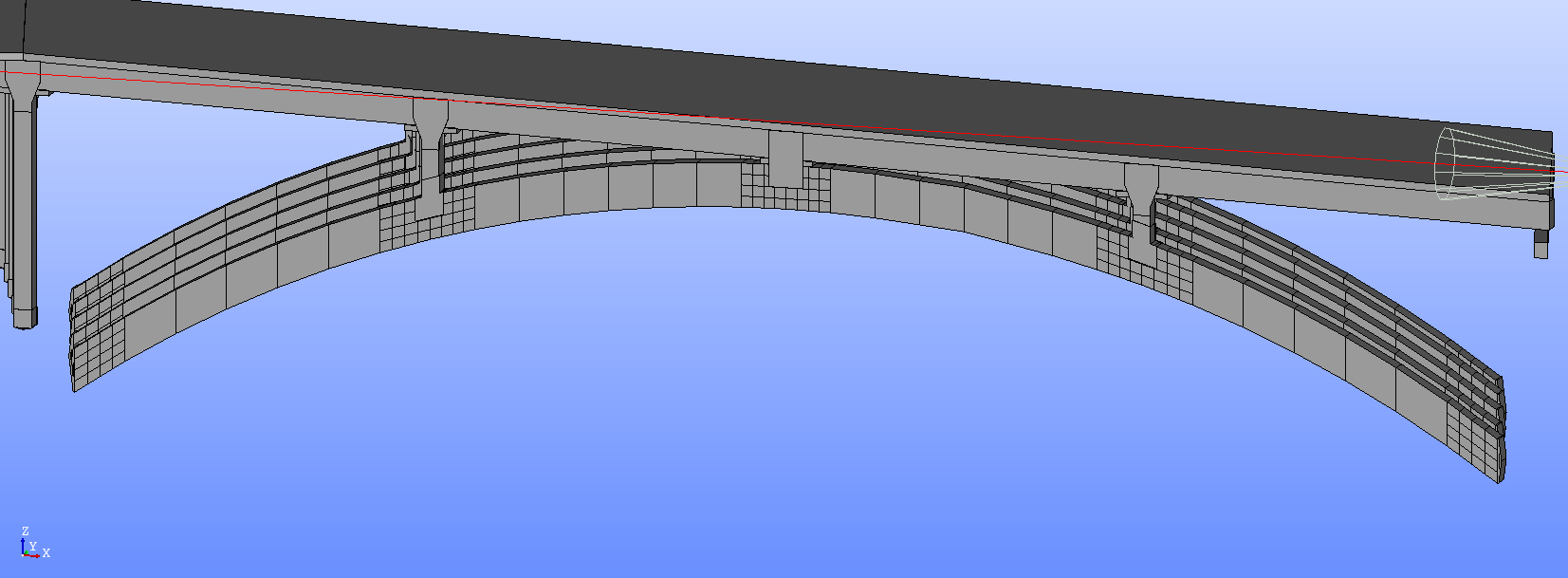
モデル化†
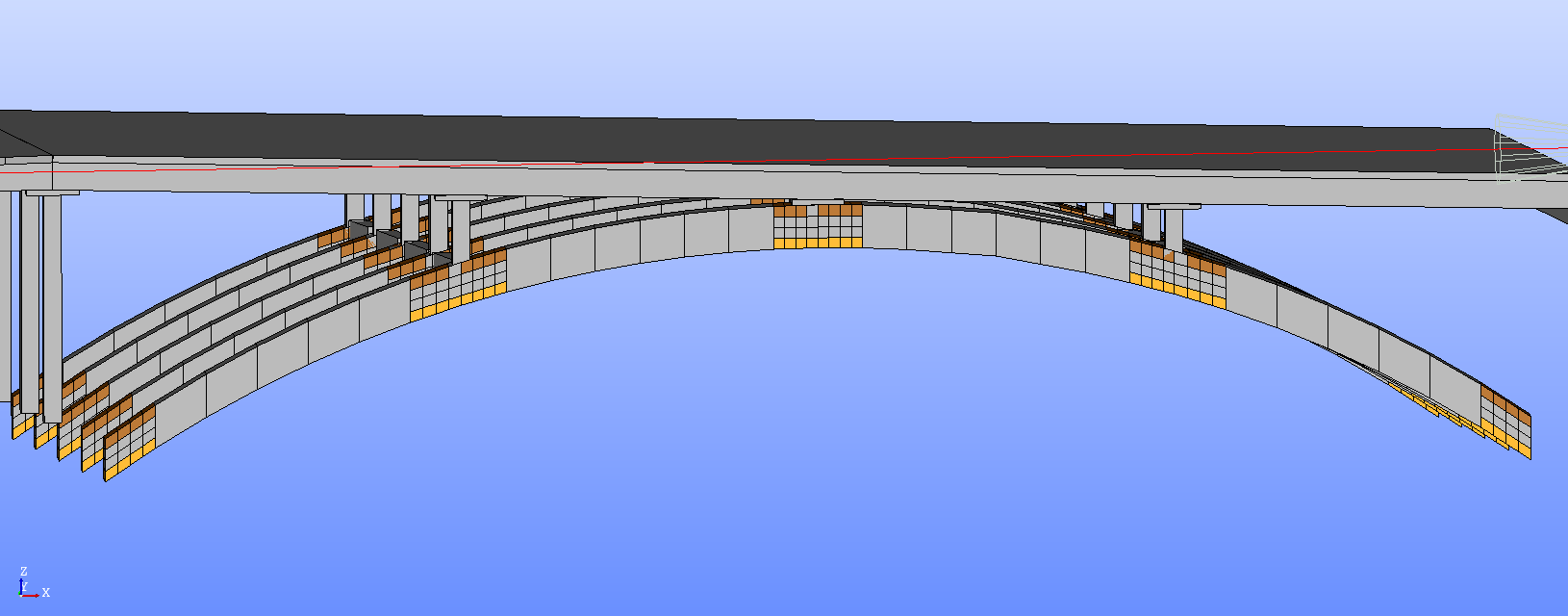
- 接合部有りの場合,構造上設定が複雑化するため接合部の鋼材を取り払ったモデルで解析を行う.
(鋼材を取り払っても固有振動数にあまり影響がないらしい)


かじか橋アーチ部分における腐朽を考慮した振動解析†
- 健全なアーチと腐朽を伴ったアーチを立体要素で表現し振動解析を行う.
→それぞれの固有振動数を比較し,腐朽による影響について考察する.
→かじか橋全体解析に活用
解析結果†
- ヤング率 E=9.6[GPa] ポアソン比 ν=0.4 密度 ρ=0.0459[tf/m3]
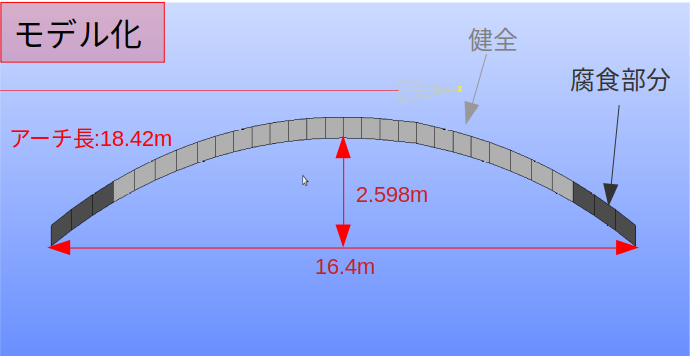
弧長18.42m、弦長16.4m、矢高2.598m、半径11.138m、中心角1.654rad、断面(0.5m,0.2m)
理論値:一次固有振動数6.60Hz、二次固有振動数29.88Hz
- 腐食部分のヤング率は健全な状態 (9.6GPa) から3/4(7.2GPa),1/2(4.8GPa),1/4(2.4GPa) と段階的に設定し , 腐食部分以外は健全な状態とする.
- 表の括弧内は健全なアーチに対する腐朽したアーチの固有振動数の相対誤差を示す.
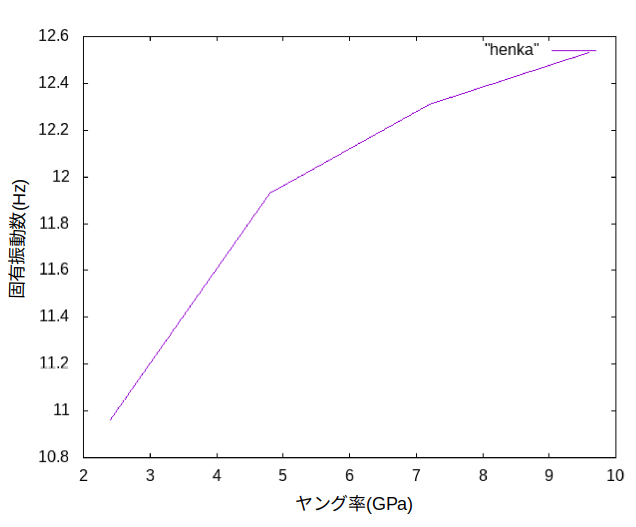
- 下のグラフは鉛直逆対称1次における各段階のヤング率に対する固有振動数の変化を示す.
| 振動モード | 健全 | 3/4(%) | 1/2(%) | 1/4(%) |
| 水平一次 | 1.21 | 1.10(-9.1) | 0.92(-24.0) | 0.67(-44.6) |
| 水平二次 | 10.04 | 9.77(-2.7) | 9.52(-5.2) | 8.90(11.4) |
| 鉛直逆対称一次 | 12.53 | 12.31(-1.8) | 11.93(-4.8) | 10.96(-12.5) |
| 鉛直対称一次 | 26.79 | 25.86(-3.5) | 24.28(-9.4) | 20.92(-21.9) |
ソリッド要素と梁要素の振動解析精度の比較(アーチ、片持ちばり)†
- 振動解析において、構造物の様子をそのまま表現できるソリッド要素での解析が理想である.
→複雑な構造物(トラス橋やアーチ橋など)を表現する場合、ソリッド要素だと計算容量が大きくなり解析精度に支障をきたす.
→複雑な部分を計算容量が小さい梁要素で代用できるか
- 佐々木さんの卒論では、長さ幅を10:1と3:1の場合で比較し、ソリッド要素に対する梁要素の相対誤差を求めた.
→今回は、より長さ幅の比較の数を多くし、?:?からだったら梁要素でも代用可能か調べる.
- 表の括弧内は、ソリッド要素に対する梁要素の相対誤差
アーチ(かじか橋のアーチ部分)†
2回目
- 前回、ヤング率や密度などの値が間違っていたため、訂正版を下の表に示す.
- ヤング率 E=9.6[GPa] ポアソン比 ν=0.4 密度 ρ=0.0459[tf/m3]
弧長18.42m、弦長16.4m、矢高2.598m、半径11.138m、中心角1.654rad、断面(0.5m,0.2m)
理論値:一次固有振動数6.60Hz、二次固有振動数29.88Hz
| 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 1.21 | 2.96(145) |
| 水平二次 | 10.04 | 8.35(-16.8) |
| 鉛直逆対称一次 | 12.53 | 12.50(-0.24) |
| 鉛直一次 | 26.79 | 27.64(3.2) |
1回目
| 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 197.804 | 80.4797(-59.3) |
| 水平二次 | 545.131 | 227.027(-58.4) |
| 鉛直一次 | 725.067 | 339.824(-53.1) |
| 鉛直二次 | 1077.69 | 751.72(-30.2) |
片持ち梁†
- 断面(10mm,20mm)
- 各長さ幅で比較し,ソリッド要素に対して梁要素でも許容できる長さ幅を見つける.
| 長さ幅3:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 221.382 | 225.539(1.9) |
| 鉛直一次 | 358.135 | 451.078(26) |
| ねじれ | 512.002 | 463.856(-9.4) |
| 水平二次 | 976.642 | 1413.43(44.7) |
| 鉛直二次 | 1148.46 | 2826.86(146.1) |
| 長さ幅4:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 128.251 | 126.866(-1.1) |
| 鉛直一次 | 221.115 | 253.731(14.8) |
| ねじれ | 379.956 | 347.874(-8.4) |
| 水平二次 | 634.711 | 795.054(25.3) |
| 鉛直二次 | 821.454 | 1590.0454(93.6) |
| 長さ幅5:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 82.6247 | 81.194(-1.7) |
| 鉛直一次 | 148.452 | 162.388(9.4) |
| ねじれ | 298.992 | 278.293(-6.9) |
| 水平二次 | 439.048 | 508.834(15.9) |
| 鉛直二次 | 615.602 | 1017.67(65.3) |
| 長さ幅6:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 57.6223 | 56.3847(-2.1) |
| 鉛直一次 | 106.167 | 112.769(6.2) |
| ねじれ | 247.042 | 231.908(-6.1) |
| 水平二次 | 319.659 | 353.357(10.5) |
| 鉛直二次 | 477.659 | 706.714(48) |
| 長さ幅7:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 42.5245 | 41.4255(-2.6) |
| 鉛直一次 | 79.4533 | 82.851(4.3) |
| ねじれ | 211.127 | 198.777(-5.8) |
| 水平二次 | 242.827 | 259.609(6.9) |
| 鉛直二次 | 380.129 | 519.219(36.6) |
| 長さ幅8:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 32.4298 | 31.7164(-2.2) |
| 鉛直一次 | 61.5021 | 63.4328(3.1) |
| ねじれ | 182.779 | 173.929(-4.8) |
| 水平二次 | 189.034 | 198.763(5.1) |
| 鉛直二次 | 308.46 | 397.527(28.9) |
| 長さ幅9:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 25.6651 | 25.0599(-2.4) |
| 鉛直一次 | 49.0123 | 50.1198(2.3) |
| ねじれ | 162.076 | 154.603(-4.6) |
| 水平二次 | 151.761 | 157.048(3.5) |
| 鉛直二次 | 254.938 | 314.095(23.2) |
| 長さ幅10:1 | 振動モード | ソリッド要素 | 梁要素(相対誤差) |
| 水平一次 | 20.8188 | 20.2985(-2.5) |
| 鉛直一次 | 39.9531 | 40.597(1.6) |
| 水平二次 | 124.4 | 127.209(2.3) |
| ねじれ | 145.725 | 139.142(-4.5) |
| 鉛直二次 | 213.841 | 254.417(19) |
作業日誌(6月)†
| 6/2 | 12:30-14:00 | 1.5 | 卒論 | |
| 6/5 | 14:30-17:00 | 2.5 | 卒論 | |
| 6/7 | 13:00-18:00 | 5.0 | 卒論経過報告 | 後藤さん |
| 6/12 | 14:00-18:00 | 4.0 | 卒論 | |
| 6/14 | 13:30-16:30 | 3.0 | 卒論経過報告 | 後藤さん |
梁の振動解析†
単純梁の振動解析(シェル要素)(x,y,z)=(600,50,0)†
- (x,y,z)=(600,50,0) [mm] 支間長500mm 厚さ1mm
ヤング率 E=206000[MPa] ポアソン比 ν=0.3 密度 ρ=7.693e-05[N/mm3]
| 振動モード | 解析値(Hz) | 理論値(Hz) | 相対誤差(%) |
| 鉛直一次 | 0.0933 | 0.0939 | -0.63 |
| 鉛直二次 | 0.3663 | 0.3754 | -2.4 |
| 鉛直三次 | 0.795 | 0.8447 | -5.9 |
よりシェル要素に近づけると、理論値との相対誤差は小さくなるということがわかった.

片持ち梁の振動解析(シェル要素)(x,y,z)=(100,10,0)†
- (x,y,z)=(100,10,0) [mm]
- ヤング率 E=6000[MPa] ポアソン比 ν=0.4 密度 ρ=3.8e-07[N/mm3]
厚さ20mm
| 振動モード | 解析値(Hz) | 理論値(Hz) | 相対誤差(%) |
| 水平一次 | 20.2899 | 20.2963 | -0.03 |
| 水平二次 | 121.436 | 127.2036 | -4.5 |
| 鉛直二次 | 170.61 | 254.4073 | -32.9 |
| 314.818 | | |
| 水平三次 | 318.971 | 356.2097 | -10.5 |
厚さ5mm
| 振動モード | 解析値(Hz) | 理論値(Hz) | 相対誤差(%) |
| 水平一次 | 20.2899 | 20.2963 | -0.03 |
| 鉛直二次 | 44.427 | 63.6018 | -30.1 |
| 水平二次 | 121.436 | 127.2036 | -4.5 |
| 鉛直三次 | 143.703 | 178.1048 | -19.3 |
| ねじれ | 168.011 | 139.0860 | 20.8 |
結果として,厚さが20mmと5mmのどちらの場合でも理論値との相対誤差は,水平方向だと小さく,鉛直方向だと大きい値となった.
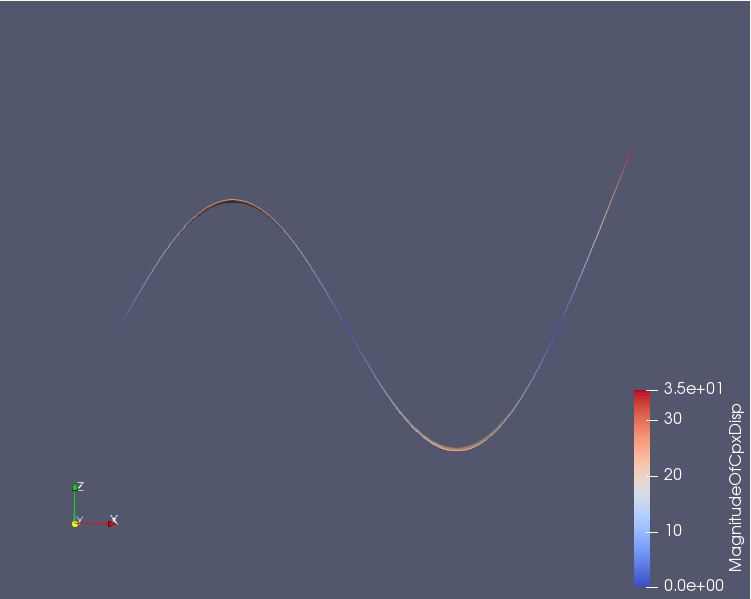
片持ち梁の振動解析(梁要素)(x,y,z)=(100,0,0)†
- (x,y,z)=(100,0,0) [mm] Asterstudyにおいて断面諸量を(10,20)に設定
ヤング率 E=6000[MPa] ポアソン比 ν=0.4 密度 ρ=3.8e-07[N/mm3]
理論値(曲げ振動)f=(1/2π)*(λ/I)^2*√(EI/ρA)
理論値(ねじれ振動)f=λ/2πL*√(GJ/ρIp)
| 振動モード | 解析値(Hz) | 理論値(Hz) | 相対誤差(%) |
| 水平一次 | 20.2985 | 20.2963 | 0.01 |
| 鉛直一次 | 40.597 | 40.5925 | 0.01 |
| 水平二次 | 127.209 | 127.2036 | 0.004 |
| ねじれ | 139.142 | 139.0860 | 0.04 |
| 鉛直二次 | 254.417 | 254.4073 | 0.004 |
梁要素でも青山さんと同じ結果となり,理論値との相対誤差はとても小さい値となった.
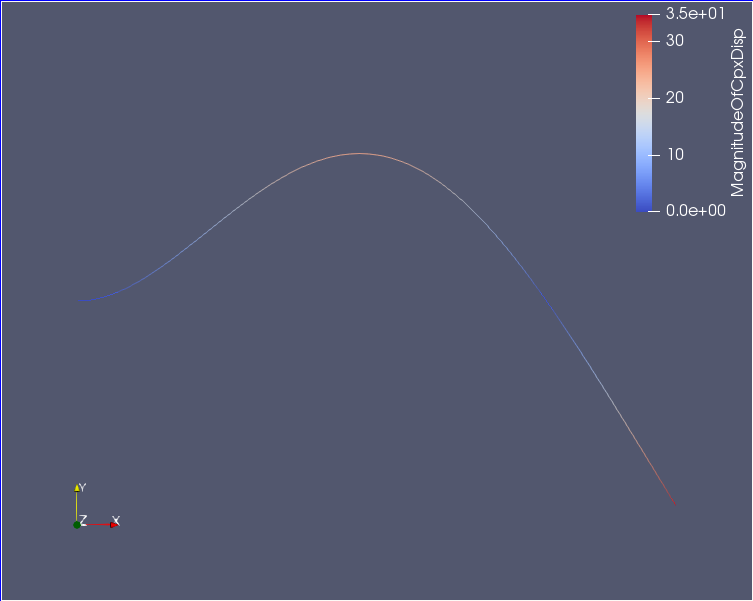
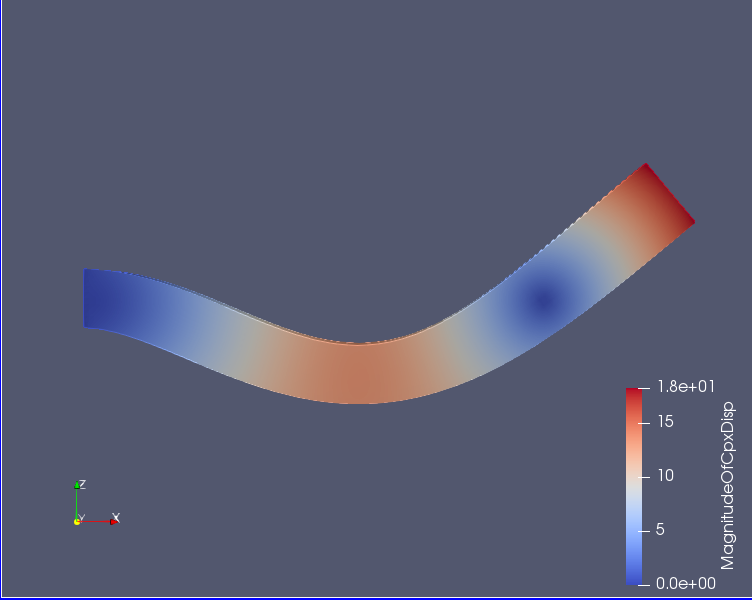
片持ち梁の振動解析(ソリッド要素)(x,y,z)=(100,10,20)†
- (x,y,z)=(100,10,20) [mm]
ヤング率 E=6000[MPa] ポアソン比 ν=0.4 密度 ρ=3.8e-07[N/mm3]
理論値(曲げ振動)f=(1/2π)*(λ/I)^2*√(EI/ρA)
理論値(ねじれ振動)f=λ/2πL*√(GJ/ρIp)
| 振動モード | 解析値(Hz) | 理論値(Hz) | 相対誤差(%) |
| 水平一次 | 20.8188 | 20.2963 | 2.57 |
| 鉛直一次 | 39.9531 | 40.5925 | -1.58 |
| 水平二次 | 124.4 | 127.2036 | -2.20 |
| ねじれ | 145.725 | 139.0860 | 4.77 |
| 鉛直二次 | 213.841 | 254.4073 | 15.95 |
青山さんの計算結果と照らし合わせると,同じ結果となり理論値との相対誤差も小さくなった.
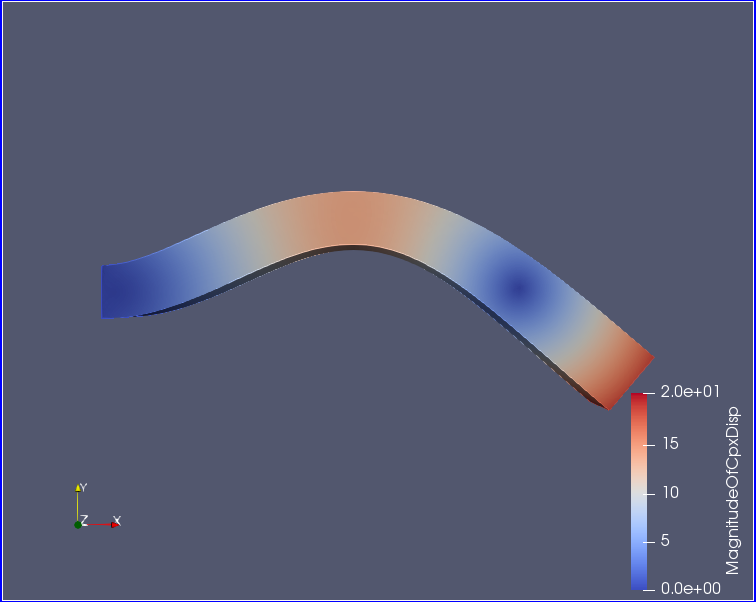
片持ち梁の振動解析(ソリッド要素)(x,y,z)=(100,10,10)†
- (x,y,z)=(100,10,10) [mm]
ヤング率 E=6000[MPa] ポアソン比 ν=0.4 密度 ρ=3.8e-07[N/mm3]
理論値(曲げ振動)f=(1/2π)*(λ/I)^2*√(EI/ρA)
理論値(ねじれ振動)f=λ/2πL*√(GJ/ρIp)
| 振動モード | 解析値(Hz) | 理論値(Hz) | 相対誤差(%) |
| 水平一次 | 0.0204138 | 0.0142 | 43.8 |
| 鉛直一次 | 0.0204138 | 0.0142 | 43.8 |
| 水平二次 | 0.122138 | 0.128202 | -4.73 |
| 鉛直二次 | 0.122139 | 0.128202 | -4.73 |
| ねじれ | 0.173527 | 0.156478 | 10.9 |
解析方法と理論値に間違い(密度とλの値)があったため、訂正後の計算結果を下の表に示す。
| 振動モード | 解析値(Hz) | 理論値(Hz) | 相対誤差(%) |
| 水平一次 | 20.4138 | 20.2963 | 0.58 |
| 鉛直一次 | 20.4138 | 20.2963 | 0.58 |
| 水平二次 | 122.139 | 127.2036 | -3.98 |
| 鉛直二次 | 122.139 | 127.2036 | -3.98 |
| ねじれ | 173.527 | 172.4301 | 0.64 |
作業日誌(5月)†
| 5/10 | 11:00-19:00 | 8.0 | 卒論 | 後藤さん |
| 5/12 | 12:00-14:00 | 2.0 | 卒論 | |
| 5/17 | 14:00-18:00 | 4.0 | 卒論 | 後藤さん |
| 5/21 | 15:30-18:30 | 3.0 | 卒論 | |
| 5/24 | 13:00-17:00 | 4.0 | 卒論 | 後藤さん |
| 5/26 | 13:00-14:30 | 1.5 | 卒論 | |
| 5/28 | 15:00-19:00 | 4.0 | 卒論 | |
| 5/31 | 13:30-18:30 | 5.0 | 卒論 | 後藤さん |
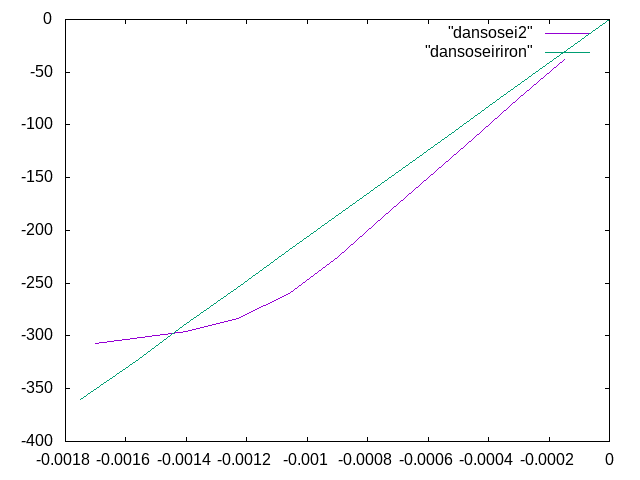
材料非線形解析(弾塑性)†
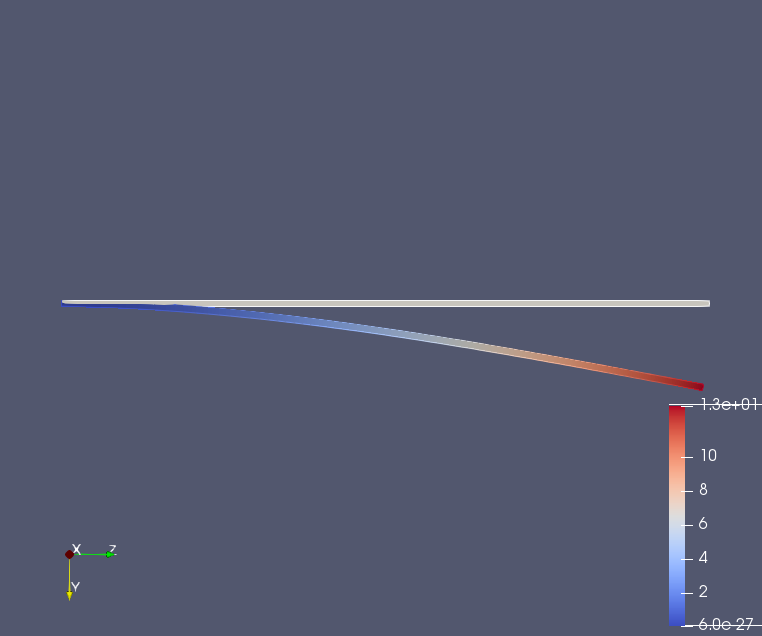
- 鋼材1mm✕1mm✕100mmの片持ち梁の先端に荷重0.6[N]をかけた.
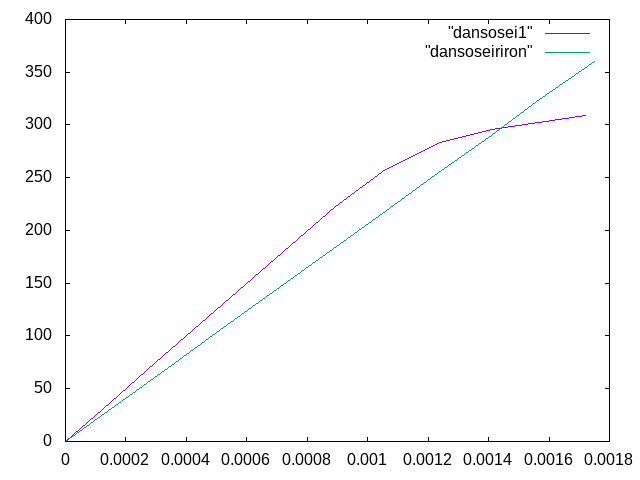
- 時間ごとに変位を解析し,固定部の縁部の軸方向応力が降伏点に達しないうちは弾性線形になり,
降伏点に達したところでグラフが折れ曲がることを確認していく.
- 理論値は,\( σ=\frac{Pl}{I}y \)より,360[N/mm\( ^{2} \)]
作業日誌(4月)†
| 4/5 | 16:00-16:30 | 0.5 | 顔合わせ(zoom) | 後藤さん、青木さん、石黒さん |
| 4/12 | 14:30-16:00 | 1.5 | 卒論テーマ紹介 | 後藤さん |
| 4/14 | 13:00-18:00 | 5.0 | 春休み課題 | |
| 4/16 | 15:00-19:00 | 4.0 | 春休み課題 | |
| 4/19 | 10:30-17:00 | 6.5 | 春休み課題発表、卒論テーマ決定 | 後藤さん |
| 4/23 | 15:00-19:00 | 4.0 | 卒論 | |
| 4/26 | 14:00-17:30 | 3.5 | 卒論 | 後藤さん |
3年次†
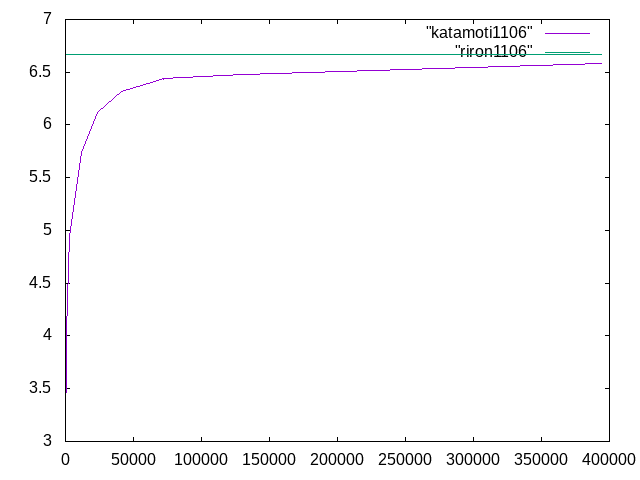
Salome-Meca 11/6†
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.5 | 394121 | 6.57938 | -1.4 | 君島 |
| 0.7 | 130916 | 6.4781 | -2.8 | 君島 |
| 0.8 | 72101 | 6.43695 | -3.5 | 高橋 |
| 0.9 | 71718 | 6.43136 | -3.6 | 高橋 |
| 1.0 | 72278 | 6.44302 | -3.4 | |
| 1.2 | 65575 | 6.408255 | -3.9 | 田村 |
| 1.4 | 41096 | 6.316155 | -5.2 | 田村 |
| 1.5 | 23417 | 6.120905 | -8.2 | 根本 |
| 1.8 | 11758 | 5.7368975 | -13.9 | 根本 |
| 2 | 11817 | 5.7382525 | -13.9 | 藤原 |
| 4 | 2862 | 4.9428 | -25.9 | 藤原 |
| 8 | 897 | 4.0411725 | -39.4 | 森島 |
| 10 | 596 | 3.4634575 | -48.1 | 森島 |
ヤング率は6000N/mm2,ポアソン比0.4,手計算での片持ち梁の変位は6.67であった.
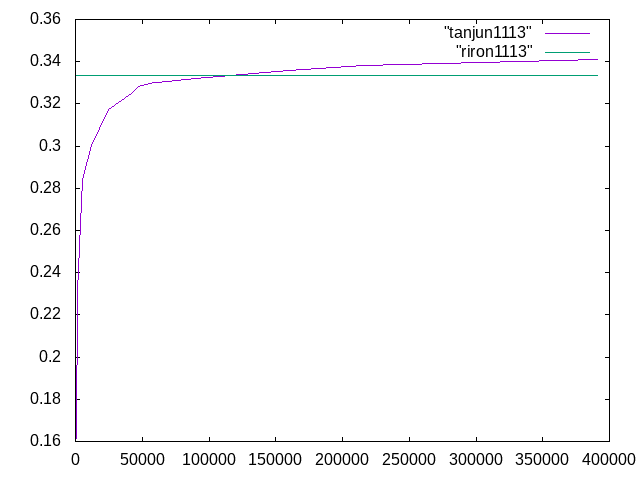
Salome-Meca 11/13†
| メッシュの長さ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.341181238095 | 2.35 | 君島 |
| 0.7 | 215780 | 0.337975375 | 1.39 | 君島 |
| 0.8 | 159468 | 0.33563 | 0.69 | 高橋 |
| 0.9 | 90071 | 0.33203 | -0.39 | 高橋 |
| 1 | 61315 | 0.32997 | -1.2 | |
| 1.2 | 58111 | 0.329956 | -1.2 | 田村 |
| 1.4 | 47409 | 0.328156 | -1.5 | 田村 |
| 1.5 | 42068 | 0.325074 | -2.4 | 根本 |
| 1.8 | 24627 | 0.317161 | -4.8 | 根本 |
| 2 | 12228 | 0.3005115 | -6.9 | 藤原 |
| 4 | 5077 | 0.28405475 | -13.9 | 藤原 |
| 8 | 1795 | 0.2312003333 | -30.6 | 森島 |
| 10 | 752 | 0.1612725 | -51.6 | 森島 |
ヤング率は7500N/mm2,ポアソン比0.4,断面積10mm×10mm,手計算での単純梁の変位は0.33…であった.
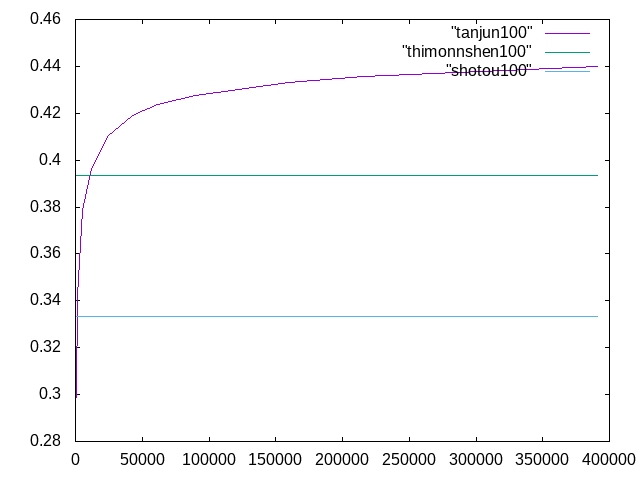
Salome-Meca 11/20†
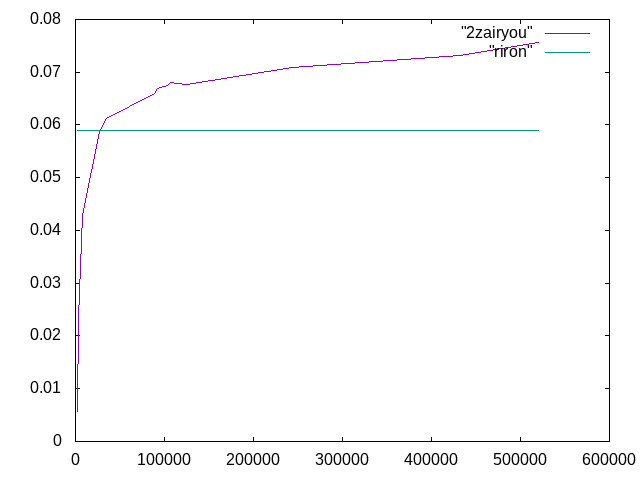
長さ100mmの場合
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.440015 | 11.9 | 君島 |
| 0.7 | 215780 | 0.435823 | 10.8 | 君島 |
| 0.8 | 159468 | 0.4330131 | 10.1 | 高橋 |
| 0.9 | 90071 | 0.42766 | 8.72 | 高橋 |
| 1 | 61315 | 0.423881 | 7.77 | |
| 1.2 | 58111 | 0.423005 | 7.54 | 田村 |
| 1.4 | 47409 | 0.420309 | 6.86 | 田村 |
| 1.5 | 42068 | 0.418470375 | 6.4 | 根本 |
| 1.8 | 24627 | 0.410464142857 | 4.4 | 根本 |
| 2 | 12228 | 0.396314 | 0.84 | 藤原 |
| 4 | 5077 | 0.378695 | -3.6 | 藤原 |
| 8 | 1795 | 0.342299 | -12.7 | 森島 |
| 10 | 752 | 0.298709 | -24 | 森島 |
初等梁の理論値は0.333333,ティモンシェン梁の理論値は0.393333であった.
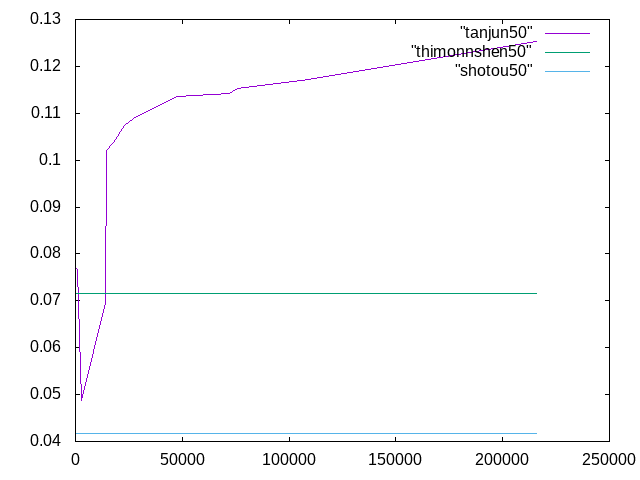
長さ50mmの場合
| メッシュの長さ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.5 | 215781 | 0.1253048 | 74.8 | 君島 |
| 0.7 | 109175 | 0.1172535 | 63.6 | 君島 |
| 0.8 | 75902 | 0.11527 | 60.8 | 高橋 |
| 0.9 | 71911 | 0.11416 | 59.3 | 高橋 |
| 1 | 47757 | 0.113602 | 58.5 | |
| 1.2 | 26945 | 0.108935 | 51.99 | 田村 |
| 1.4 | 22998 | 0.107298 | 49.71 | 田村 |
| 1.5 | 17689 | 0.10375025 | 44.77 | 根本 |
| 1.8 | 14668 | 0.1021334 | 42.51 | 根本 |
| 2 | 13986 | 0.069684 | -2.8 | 藤原 |
| 4 | 3009 | 0.048789575 | -32.0 | 藤原 |
| 8 | 967 | 0.0764429 | 7.2 | 森島 |
| 10 | 558 | 0.0768385 | 6.7 | 森島 |
初等梁の理論値は0.041666,ティモンシェン梁の理論値は0.071666であった.
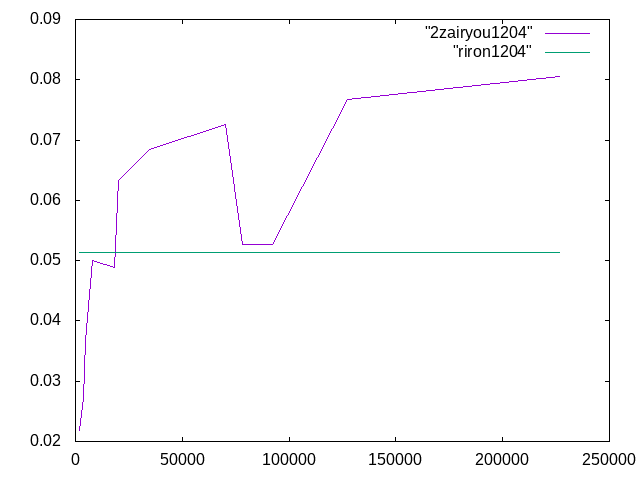
Salome-Meca 12/4†
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.8 | 226647 | 0.08053 | 56.9 | 高橋 |
| 0.9 | 127506 | 0.07678 | 49.7 | 高橋 |
| 1 | 92447 | 0.05276 | 2.79 | |
| 1.2 | 88386 | 0.05264 | 2.55 | 田村 |
| 1.4 | 78086 | 0.05261 | 2.49 | 田村 |
| 1.5 | 70032 | 0.072549 | 41.3 | 根本 |
| 1.8 | 34858 | 0.068375 | 33.2 | 根本 |
| 2 | 20313 | 0.063280 | 23.3 | 藤原 |
| 3 | 18229 | 0.048924 | -4.68 | 君島 |
| 4 | 8067 | 0.050046 | -2.51 | 藤原 |
| 5 | 4846 | 0.036773 | -28.3 | 君島 |
| 8 | 3814 | 0.027088 | -47.2 | 森島 |
| 10 | 1716 | 0.021791 | -57.5 | 森島 |
理論値は0.051335であった.
創造工房†

作業日誌(3年次)†
| 日付 | 時間帯 | 作業時間 | 内容 | 立会 |
| 10/16 | 14:30-16:00 | 1.5 | 顔合わせ、ノートPCの使い方 | 後藤さん、M2、その他 |
| 10/23 | 14:30-16:00 | 1.5 | UNIXコマンドの使い方 | 後藤さん |
| 10/30 | 14:30-16:00 | 1.5 | viの使い方 | 後藤さん |
| 11/6 | 14:00-18:00 | 4.0 | Salome-mecaの使い方 | 後藤さん |
| 11/12 | 14:30-18:00 | 3.5 | 課題 | |
| 11/13 | 14:00-18:00 | 4.0 | Salome-meca 単純梁 | 後藤さん |
| 11/19 | 16:00-19:30 | 3.5 | 課題 | |
| 11/20 | 13:30-16:30 | 3.0 | Salome-meca 木材 直交異方性 | 後藤さん |
| 11/26 | 15:00-18:00 | 3.0 | 課題 | |
| 12/3 | 16:30-21:30 | 5.0 | 課題 | |
| 12/4 | 13:00-17:30 | 4.5 | Salome-meca 2材料(木材、鋼材) | 後藤さん |
| 12/10 | 16:00-19:00 | 3.0 | 課題 | |
| 12/11 | 13:30-18:30 | 5.0 | LaTeX XHTMLの練習 | 後藤さん |
| 12/17 | 16:30-18:30 | 2.0 | 課題 | |
| 12/18 | 14:30-16:30 | 2.0 | LaTeX XHTMLの練習 | 後藤さん |
| 1/22 | 14:30-16:30 | 2.0 | 最終課題 | 後藤さん |
| 1/28 | 16:00-18:30 | 2.5 | 最終課題 | |
| 1/29 | 14:30-19:00 | 4.5 | 最終課題 | 後藤さん |
| 2/5 | 14:30-17:30 | 3.0 | 最終課題 | 後藤さん |
| 2/10 | 16:30-18:30 | 2.0 | 最終課題 | 後藤さん |
| 2/12 | 14:30-17:00 | 2.5 | 発表 | 後藤さん |
| 3/9 | 14:00-16:00 | 2.0 | 春休み課題 | 後藤さん |
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)