![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
2/22 毎日追われるように解析と修正の繰り返しの日々だったが、無事卒論発表を終えることができた。 wikiの更新が全然できてなくて結果ばかりになってしまったが、できる限りわかりやすくまとめ直していこうと思う。
(覚えている範囲の手直しなので間違いが出るかも もっとノートとかwikiを真面目に書いておくんだった)
12/22 とりあえず中間発表終了
12/20 中間発表用のLaTeXとスライドの作成
12/13 データまとめはとりあえず終わったが決定係数\( R^2 \)とは何なのだろうか。そこら辺を調べつつ中間発表に向けて準備を進めていく。
12/6 自分のパソコンだと解析に3週間程度かかるので及川さんのパソコンで解析を回しつつASTERCODEの作成とデータまとめをしていく
11/29 解析は終わっていたが間違えて1次要素でやっていた。2次要素で解析をやり直しているが長い。これからはミスできない解析になってきたようだ。
11/22 かじか橋のアーチ部分に異方性用のBOX作成完了。 AsterStudyの変更も多分完了したので今日解析して帰って金曜日までに終わっていることを願う
11/15 青山さんの論文を読んだのでこれからアーチに異方性を適用できるように頑張る
11/8 ワクチンによる体調不良
11/1 ウォルトキングの論文を梁要素で再現してみた
10/25 ウォルトキングの論文を一通り読み終えた
10/18 理論値と大きく離れたので論文を頑張って翻訳中
10/11 ウォルトキングの理論値関連
とりあえずねじれが卓越した原因がせん断弾性係数Gの影響だったのかGの値を変えながら感度解析してみるか?(今は異方性だと\( G = \frac{E}{15} \)、等方性だと大体\( G= \frac{E}{3} \))
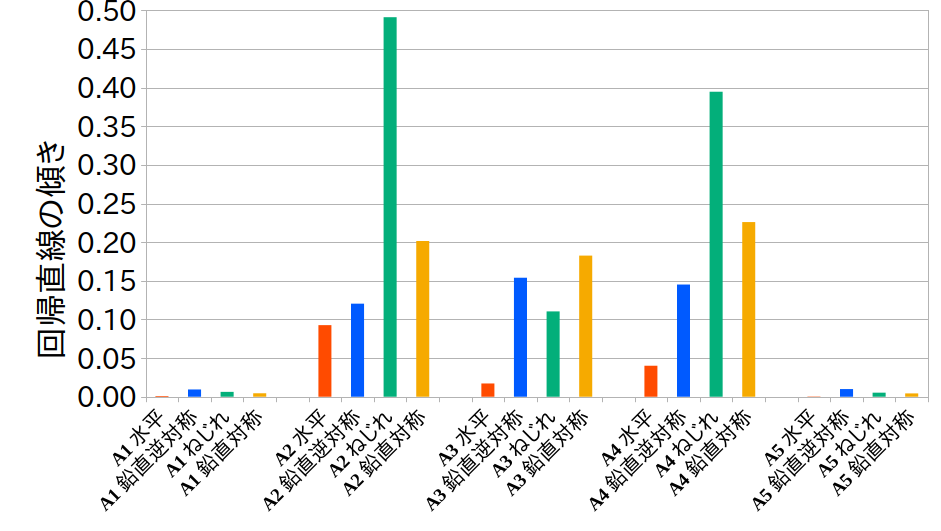
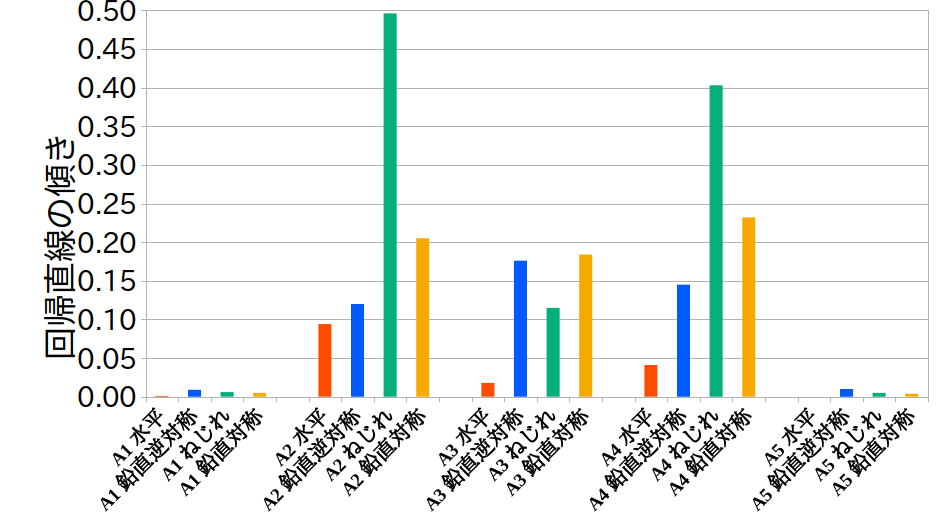
最初の解析は\( G= \frac{E}{10} \)とかで作ってやってみるとか?(3/5 10:51start 3/6 16:23end) 上が\( G = \frac{E}{10} \) 下が\( G = \frac{E}{15} \)
3/8 思ったより差が出なかったので\( G = \frac{E}{5} \) 下が\( G = \frac{E}{7} \)も作ってやってみる。(アーチのGしか変えていないのが原因なのか?)
3/11 salomeが落ちてた… 何も結果は出てないし、どこで終わったのかもわからないので今まで通りやるしかない(120個の結果を一気に得ようとして失敗)
3/15 とりあえずでやったものが下のグラフだが、Gを変えたのが床版以外だからこうなったのか? 床版もGを同じで変えてみるしかない
3/18 床版も全てのGを同じ倍率で変えてみたら下のグラフのようなグラフが得られた。自分的には\( G=\frac{E}{15} \)から等方性(\( G=\frac{E}{3} \))にかけて徐々に落ちていくと思っていたが、何故か増えた。 原因を探さなきゃ…
3/25 とりあえず全データを取り終えた。傾きはせん断弾性係数を大きくしたほうが大きくなっているが、他の振動モードとねじれモードの比率を見るとねじれが卓越しているのはせん断弾性係数が小さいほうが卓越したのでねじれモードが卓越したのはせん断弾性係数の影響なのではないかと考えられる。
アーチだけ取り出して今は15BOXでアーチの角度変えているけどもっとすくないBOX数でも問題ないとかの検討もする必要あるのかな?
振動解析(青山さん、七五三さんの続き) 不朽箇所1箇所ごとの感度は青山さんの手法で調べられるのだけど、それらの組み合わせの影響を何らかの統計的な手法(ベイズ推定とか)で評価できないかとか。
参考: 経年による木製アーチ道路橋(かじか橋)の構造性能と健全度調査
ヤング率の減少のみで逆対象1次を測定値8.69Hzに合わせた場合
| 固有振動数(Hz) | 水平1次モード | 鉛直逆対称1次モード | ねじれ逆対称1次モード | 鉛直対称1次モード |
| アーチ異方性 | 6.01510 | 8.69551 | 9.45167 | 13.8143 |
| 測定値(2019) | 2.73 | 8.69 | 10.64 | 15.38 |
| アーチ等方性 | 6.64165 | 8.69488 | 12.3674 | 14.9576 |
ねじれが10.64Hzに合ってくれたらうれしい
等方性だと振動数が高く、異方性だと振動数が低い
ねじれの誤差
アーチ等方性 16.23%
アーチ異方性 12.57%
床版は異方性を適用済み
腐朽なしのときの固有振動数
| 固有振動数(Hz) | 水平1次モード | 鉛直逆対称1次モード | ねじれ逆対称1次モード | 鉛直対称1次モード |
| アーチ等方性 | 9.44718 | 12.9978 | 18.4994 | 21.5656 |
| アーチ異方性 | 9.17776 | 12.3707 | 15.7861 | 18.2731 |
| 全体異方性 | 7.56782 | 11.1306 | 13.0727 | 17.5401 |
各状態からの減少率
| 減少率(%) | 水平1次モード | 鉛直逆対称1次モード | ねじれ逆対称1次モード | 鉛直対称1次モード |
| アーチ等方性→アーチ異方性 | 2.85 | 4.82 | 14.67 | 15.27 |
| アーチ等方性→全体異方性 | 19.89 | 14.37 | 29.33 | 18.67 |
| アーチ異方性→全体異方性 | 17.54 | 10.02 | 17.19 | 4.01 |
ねじり剛性とは、\( K = G \times J \)
Kがねじり剛性、Gは材料のせん断弾性係数、Jがサン・ブナンのねじり定数
\( G = \frac{E}{2 \times (1 + \nu )} \)
\( \nu \) はポアソン比
アーチに異方性を適用して振動解析を行った。アーチが腐朽していくパターンと桁が腐朽していくパターン
縦軸:固有振動数(Hz)、横軸:ヤング率の残存率
及川さんの英語論文より5%程度固有振動数が減少したかな?
決定係数\( R^2 \)は、数値予測のモデルの良さを測る指標の一つ。高ければ高いほどよく、最良の場合 1 になる。評価用データに含まれる正解の値と、予測モデルが予測した値との間にどれくらい相関があるかを確認するために用いられる。
論文を読んでからやり直し
(E=9.6*10^9N/m^2 , b=0.1m , h=0.65m ,RHO=459Kg/m^3 ,弧長\( \ell \)=16m , 矢高f=2m)
| \( f/\ell \)=1/8 | 対称1次 | 対称2次 | 逆対称1次 | 逆対称2次 |
| 解析値(Hz) | 34.4245 | 48.1666 | 18.2823 | 76.3628 |
| 理論値(Hz) | 40.012 | 117.369 | 18.6724 | 77.3571 |
| 誤差(%) | 13.96 | 58.96 | 2.09 | 1.28 |
(E=9.6*10^9N/m^2 , b=0.1m , h=0.65m ,RHO=459Kg/m^3 ,弧長\( \ell \)=15m , 矢高f=3m)
| \( f/\ell \)=1/5 | 対称1次 | 対称2次 | 逆対称1次 | 逆対称2次 |
| 解析値(Hz) | 36.3346 | 65.0017 | 16.0021 | 71.0228 |
| 理論値(Hz) | 37.881 | 111.081 | 15.665 | 71.206 |
| 誤差(%) | 4.08 | 41.48 | 2.15 | 0.26 |
(E=9.6*10^9N/m^2 , b=0.1m , h=0.61m ,RHO=459Kg/m^3 ,弧長\( \ell \)=16m , 矢高f=1m)
| \( f/\ell \)=1/16 | 対称1次 | 対称2次 | 逆対称1次 | 逆対称2次 |
| 解析値(Hz) | 20.5211 | 46.8057 | 20.3054 | 82.1309 |
| 理論値(Hz) | 44.014 | 117.369 | 18.672 | 82.692 |
| 誤差(%) | 53.38 | 60.12 | 8.75 | 0.68 |
対称2次は全部上手く行ってないが、その他のモードに関しては上手くいっているのではないかと思う。 特に逆対称2次に関しては誤差がかなり小さい解析ができている。誤差が小さいときにはウォルトキングの論文にあったモード(P18)と同じ振動をしていたのでsalomeでも上手く再現できることがわかった。梁要素で成功したので次はsolidで解析して異方性の適応まで行う。(メモ:細長比や断面積を注意しないと上手く行かない可能性大)
load1 = AFFE_CHAR_MECA(DDL_IMPO=(_F(DRX=0.0,
DRZ=0.0,
DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_NO=('koteiL', )),
_F(DRX=0.0,
DRZ=0.0,
DX=0.0,
DY=0.0,
DZ=0.0,
GROUP_NO=('koteiR', ))),
MODELE=model)
構造力学集P269にあるウォルトキング(waltking)の円弧2ヒンジアーチの振動数に関する図から固有振動数を求める。 解析は梁要素で確認を行った。(E=9.6*10^9N/m^2 , b=0.625m , h=0.16m ,RHO=459Kg/m^3 ,弧長=16m , 矢高=2m)
| f/l=1/8 | 対称1次 | 対称2次 | 逆対称1次 | 逆対称2次 |
| 解析値(Hz) | 4.46454 | 11.7934 | 4.53596 | 18.9013 |
| 理論値(Hz) | 9.84918 | 28.8909 | 4.59629 | 19.0417 |
| 誤差(%) | 54.67 | 59.18 | 1.31 | 0.74 |
直線梁を作成して等方性と異方性の振動の違いを確認。
B=10mm,H=5mm,L=500,RHO=4.59/mm^3,E=9600N/mm^2,NU=0.4 メッシュは2次要素でやればそんなに振動数が変わらないのでメッシュ1で確認する。
| 鉛直1次 | 鉛直2次 | 水平1次 | 水平2次 | |
| 等方性(Hz) | 41.4685 | 165.794 | 82.8916 | 330.865 |
| 異方性(Hz) | 41.4215 | 165.046 | 82.5045 | 328.842 |
| 等方性と異方性の差(%) | 0.11 | 0.45 | 0.47 | 0.61 |
かじか橋をやるということで5本のアーチでやっていたが、アーチへの異方性の適用を確認するためにはアーチ一本で確認するほうがいいと思うのでその方向で進んでみる。(6/28)
とりあえず単純梁を作成して異方性にした際の振動数の減少を確認する。(7/18〜8/2まで取っていたデータは固定方法を間違っていたためやり直し)(8/3)
等方性の鉛直振動は固定の仕方を間違っていたのでやり直し(8/4)
全データ取り終わり。等方性より異方性のほうが振動数が減少することが確認できた。2次要素だと理論値を下回る結果だが異方性のほうが振動数が減少する傾向は同じ。 次はアーチを作成して同じようになるのかを確認。(8/9)
アーチにオイラー角を用いて振動解析してみた。等方性だと鉛直1次が3101.59Hzに対して異方性を与えると3068.31Hzと少し減少したが理論値等を求めていないのでそもそもあっているかわからない。理論値を探してみて確認したほうが良さそう。(8/17)
とりあえずアーチのみのデータは取り終わった。1次要素・2次要素ともにオイラー角を用いて異方性を適用すると、振動数が明確に落ちることが確認できた。また、振動をやるときには2次要素でやったほうが収束しているので2次要素での解析で要素数を少なくして解析したほうが解析時間も短くなるのでいい気がする。(今回のデータだと大体1~2Hzくらいしか変わっていないのでそこは無視してもいい気がする。)(8/25)
構造力学公式集にあった2ヒンジアーチの固有振動数の式から1次と2次の理論値の式の計算は終わった。計算量が多く、手計算でやったのでもう一度計算してあってるかの確認をしておく必要がある(一応単位計算したら合ってたので多分大丈夫だと思うが、念の為もう一度やる)。エクセルに計算式も一応作っておいたので間違いがなかったら理論値は簡単に計算できる(File:2hinjiarchriron)。ヒンジがよくわかっていないのでそこの勉強と設定方法の確認をして中間発表に間に合うか間に合わないか早めに決めておく。(9/5)(最近あまり休めていなかったので少し休みを入れていきます)
構造力学集にあったウォルトキングの図から振動数を求めたら対称1次振動で58.9Hzであったが、解析では1200Hzぐらいだったので大きく違う。理論値に入れる値が間違っているのか解析の設定が間違っているのか分からないのでようチェック。とりあえず他の文献も読みながら理論式を探して見ようと思う。(9/15)
参考
ここから下はアーチにオイラー角で異方性を15BOXで与えたときの記録(E=9.6GPa,RHO=4.59ton/mm^3, b=0.2mm, h=0.5mm)
横軸:要素数 縦軸:振動数
ここから下は単純梁の記録(E=9.6GPa,RHO=4.59ton/mm^3, b=20mm, h=10mm, L=500mm)
縦軸:時間(分) 横軸:要素数
縦軸:振動数 横軸:要素数
アーチは一つのものとして作成されているため、場所ごとにboxを作成して異方性を適用する。
アーチを選択→点を作成(左から2番目のものを選ぶと角のものを選べる)→点を線でつなぎ4辺作成→フェースを作成で面を作成→partitionでアーチと面を選ぶ
以上によって面で区切りとなってboxを作成することができる。
もしかしたら青山さんのモデルを異方性にしていくこともするかも(オイラー角をつかって?)
Z軸回転のみ(部材がXY平面上にあるとき)のオイラー角の適用はできたのでアーチの異方性適用についてもこの方向でやっていく。
多分一つの回転のみなら簡単にできるのかもしれない
→x軸回転のみもできたのでZ軸またはX軸方向の回転はできる(y軸回転がないので少し不便だが、頑張ってZ,X軸で上手く回転させて適応させてみるしかないまたはy軸を回転するような部材を作成しないように頑張るしかないと思う)
追加
boxを斜め方向(どの平面にも触れないように)作成し、オイラー角がきちんとできるのかも確認する。急ぎではないが早めにやる。
片持ち梁を上の図のように作成して、曲げの応力-ひずみからヤング率を求めたところ完全に6000MPaと240MPaは得られなかったものの、6050MPaや245MPa付近で値を得られたのでオイラー角はうまく適応できたと考えられる。
オイラー角の回転はZ軸→X’軸→Z’’軸の順番に行っていることに注意して与える必要がある(salomeだと0→Z軸、1→X’軸、2→Z''軸の順番)
オイラー角:座標軸で回転させて向かせたい方向に回転させる。その時の角度をオイラー角と呼ぶ。
x軸を回転させる:φ角
y軸を回転させる:θ角
z軸を回転させる:ψ角
(飛行機の場合、上からバンク角、ピッチ角、機首方位角と呼ばれている)
回転させる時、原点から軸の正方向を見て右回転させていく。
片持梁の曲げで確認 応力とひずみからヤング率を計算したところ、軸方向ヤング率6000MPaに対してオイラー角を設定すると軸方向ヤング率240MPaを得ることができたので上手く設定できたと考えられる。
アーチを作成して適用してみる。
最初の名前が表面の状態
数字がモード(1:1次モード、2:2次モード)
e(鉛直)s(水平)方向
断面図↓
横軸:振動数 縦軸:中心の含水率
気乾比重は、乾燥させたときの比重のため少し(含水率10%程度)の水分を含んでいる。
全乾比重は、完全に乾燥させたときの比重(含水率0%)となっている。
スギでモデル作成していく.10✕20✕1000をモデルとし、気乾比重を最低値として考える。(5/9)(自分用メモ:解析していったデータは10bunnkatu dataに理論値とかの計算はsinndourironnkeisannにある)
| 種類 | 密度g/cm3 |
| バルサ | 0.10 |
| リグナムバイタ | 1.25 |
| キリ | 0.23 |
| アカガシ | 0.97 |
| スギ | 0.34 |
| ヒノキ | 0.42 |
| ケヤキ | 0.66 |
| ミズナラ | 0.70 |
図心をZ軸に合わせて固定もZ軸上でのものとする(Boxの中心上にできるようにする)。そこから相対誤差がどのくらい変化するかの確認。(4/27)
追記:振動解析班のものは鉛直、水平のモードで分類してなかったので理論値計算を含めやり直す。(5/1)
相対誤差まで完成。ほとんど誤差のない結果となった。(5/2)
再解析データ
理論値
鉛直1次:36.036Hz 水平1次:72.073Hz 鉛直2次:144.146Hz 水平2次:288.292Hz
1次モード
| メッシュの長さ | 鉛直1次モード | 相対誤差 | 水平1次モード | 相対誤差 |
| 0.8 | 36.0307 | 0.015% | 72.0219 | 0.067% |
| 0.9 | 36.0307 | 0.015% | 72.0219 | 0.067% |
| 1.0 | 36.0307 | 0.015% | 72.0219 | 0.067% |
| 2.0 | 36.0310 | 0.014% | 72.0224 | 0.066% |
| 3.0 | 36.0308 | 0.014% | 72.0224 | 0.066% |
| 4.0 | 36.0312 | 0.013% | 72.0226 | 0.066% |
| 5.0 | 36.0313 | 0.013% | 72.0227 | 0.066% |
2次モード
| メッシュの長さ | 鉛直2次モード | 相対誤差 | 水平2次モード | 相対誤差 |
| 0.8 | 144.053 | 0.065% | 287.477 | 0.283% |
| 0.9 | 144.053 | 0.065% | 287.477 | 0.283% |
| 1.0 | 144.053 | 0.065% | 287.477 | 0.283% |
| 2.0 | 144.058 | 0.061% | 287.484 | 0.280% |
| 3.0 | 144.055 | 0.063% | 287.485 | 0.280% |
| 4.0 | 144.060 | 0.060% | 287.488 | 0.279% |
| 5.0 | 144.062 | 0.058% | 287.490 | 0.278% |
振動解析班のデータ1次モード
| メッシュの長さ | 要素数 | 一次モードの固有振動数解析値 | 相対誤差 |
| 0.8 | 256077 | 36.0194 | 0.0294% |
| 0.9 | 128086 | 36.0194 | 0.0294% |
| 1.0 | 89462 | 36.0195 | 0.0291% |
| 2.0 | 21074 | 36.0196 | 0.0288% |
| 3.0 | 24457 | 36.0196 | 0.0288% |
| 4.0 | 5473 | 36.0199 | 0.0280% |
| 5.0 | 5725 | 36.02 | 0.0277% |
振動解析班のデータ二次モード
| メッシュの長さ | 要素数 | 二次モードの固有振動数解析値 | 相対誤差 |
| 0.8 | 256077 | 108.067 | 4.03% |
| 0.9 | 128086 | 108.183 | 3.93% |
| 1.0 | 89462 | 108.358 | 3.78% |
| 2.0 | 21074 | 109.174 | 3.05% |
| 3.0 | 24457 | 109.061 | 3.15% |
| 4.0 | 5473 | 109.906 | 2.40% |
| 5.0 | 5725 | 110.024 | 2.30% |
ねじれの理論式 \( f= \frac{\lambda}{2\pi\ell}\times \sqrt{\frac{GJ}{\rho I_p}} \)
棒材の場合はJ=\( I_p \)であるため\( f= \frac{\lambda}{2\pi\ell}\times \sqrt{\frac{G}{\rho}} \)
構造振動学(https://www.str.ce.akita-u.ac.jp/~gotouhan/j2023/aono/wiki/jsme-or-jp.pdf )
固有振動数 理論式 日本機械学会のものが見当たらなくなったのでとりあえずおいておく
ベイズ推定による既存構造物数値モデルの不確定性定量化とキャリブレーション
(Model Verification & Validation(V&V))
Alvin, K. F., Oberkampf, W. L, Dieger, K., Rutherford, B.:Uncertainty quantification in computational structural dynamics: a new paradigm for model validation, Society for Experimental Mechanics, Inc, 16 th International Modal Analysis Conference.. Vol. 2. 1998. (計算構造力学における不確かさの定量化:モデル検証のための新しいパラダイム、実験力学研究会、16th国際モード解析会議. Vol.2. 1998.)
タッチタイプ練習
・課題
・練習
| メッシュの長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 59504 | 6.56 | -1.5 | 千代岡 |
| 0.6 | 45512 | 6.48774 | -2.69 | 高井 |
| 0.7 | 39075 | 6.54133 | -2.0 | 関合 |
| 0.8 | 13397 | 6.43695 | -3.5 | 岡田 |
| 0.9 | 9903 | 6.36315 | -4.6 | 松田 |
| 1.2 | 6256 | 6.3043375 | -5.4 | 青野 |
| 1.3 | 5767 | 6.29784 | -5.6 | 山口 |
| 1.4 | 5199 | 6.29990 | -5.55 | 山本 |
| 1.5 | 3935 | 6.24807 | -6.3 | 進藤 |
| 1.6 | 3400 | 6.20446 | -6.98 | 河合 |
| 1.8 | 2952 | 6.17161 | -7.5 | 山口 |
| 2 | 1632 | 5.64585 | -15.3 | 進藤 |
| 3 | 682 | 5.47288 | -17.9 | 山本 |
| 4 | 264 | 3.6161 | -45.8 | 関合 |
| 5 | 191 | 3.86 | -42 | 千代岡 |
| 6 | 190 | 2.5077325 | -62.4 | 高井 |
| 7 | 75 | 1.41225 | -78.8 | 青野 |
| 8 | 56 | 1.2887175 | -80.7 | 岡田 |
| 9 | 49 | 1.28799 | -80.9 | 松田 |
| 10 | 44 | 1.226075 | -81.6 | 河合 |
片持ち梁のグラフ:縦軸 変位 横軸 要素数
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 604167 | 0.428982 | 2.94 | 千代岡 |
| 0.6 | 361584 | 0.421233 | 1.09 | 高井 |
| 0.7 | 145234 | 0.4225 | 1.4 | 関合 |
| 0.8 | 140987 | 0.422627385 | 1.4 | 岡田 |
| 0.9 | 91857 | 0.420351606 | 0.88 | 松田 |
| 1.2 | 24520 | 0.404744325 | -2.87 | 青野 |
| 1.3 | 23132 | 0.4045 | -2.93 | 山口 |
| 1.4 | 17530 | 0.3986 | -4.34 | 山本 |
| 1.5 | 15433 | 0.396317756757 | 4.9 | 進藤 |
| 1.6 | 15900 | 0.399049 | -4.24 | 河合 |
| 1.8 | 11677 | 0.404457 | -0.03 | 山口 |
| 2 | 10460 | 0.394818715517 | -5.3 | 進藤 |
| 3 | 2344 | 0.32447 | -22.13 | 山本 |
| 4 | 1453 | 0.3329 | -20.1 | 関合 |
| 5 | 431 | 0.136240 | -67.3 | 千代岡 |
| 6 | 360 | 0.2130486 | -48.9 | 高井 |
| 7 | 196 | 0.1019892 | -75.5 | 青野 |
| 8 | 104 | 0.1158624 | -72.2 | 岡田 |
| 9 | 81 | 0.1247076 | -70.1 | 松田 |
| 10 | 78 | 0.07733 | -81.4 | 河合 |
片持ち梁のグラフ:縦軸 変位 横軸 要素数
二次要素の等方性のデータ
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 604167 | - | - | 千代岡 |
| 0.6 | 203209 | 0.42383 | 0.98 | 高井 |
| 0.7 | 145234 | 0.43301 | 3.22 | 関合 |
| 0.8 | 140987 | 0.43006 | 3.2 | 岡田 |
| 0.9 | 91974 | 0.429913 | 3.18 | 松田 |
| 1.2 | 24800 | 0.429777 | 3.14 | 青野 |
| 1.3 | 23132 | 0.42989 | 3.16 | 山口 |
| 1.4 | 17617 | 0.429745 | 3.13 | 山本 |
| 1.5 | 15433 | 0.429844 | 3.2 | 進藤 |
| 1.6 | 15900 | 0.429754 | 3.13 | 河合 |
| 1.8 | 11677 | 0.42962 | 3.1 | 山口 |
| 2 | 10460 | 0.429605 | 3.1 | 進藤 |
| 3 | 2486 | 0.429217 | 3.0 | 山本 |
| 4 | 1453 | 0.4293 | 3.02 | 関合 |
| 5 | 431 | 0.427885 | 2.69 | 千代岡 |
| 6 | 360 | 0.4282 | 2.78 | 高井 |
| 7 | 196 | 0.42606 | 2.25 | 青野 |
| 8 | 104 | 0.42631 | 2.3 | 岡田 |
| 9 | 81 | 0.42513 | 2.03 | 松田 |
| 10 | 78 | 0.424466 | 1.8 | 河合 |
異方性1次のデータ
| メッシュ長さ | 要素数 | 変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 604167 | 0.50919 | 3.56 | 千代岡 |
| 0.6 | 203209 | 0.50472 | 2.6 | 高井 |
| 0.7 | 145234 | 0.5036 | 2.42 | 関合 |
| 0.8 | 140987 | 0.50283 | 2.3 | 岡田 |
| 0.9 | 91974 | 0.50053 | 1.8 | 松田 |
| 1.2 | 24800 | 0.48739 | -0.9 | 青野 |
| 1.3 | 23132 | 0.48841 | -0.67 | 山口 |
| 1.4 | 17617 | 0.48403 | -1.56 | 山本 |
| 1.5 | 15433 | 0.48202 | -2.0 | 進藤 |
| 1.6 | 15900 | 0.48329 | -1.7 | 河合 |
| 1.8 | 11677 | 0.47855 | -2.67 | 山口 |
| 2 | 10460 | 0.47906 | -2.6 | 進藤 |
| 3 | 2436 | 0.42787 | -12.98 | 山本 |
| 4 | 1453 | 0.42772 | -13.02 | 関合 |
| 5 | 431 | 0.27364 | -44.3 | 千代岡 |
| 6 | 360 | 0.33927 | -31.0 | 高井 |
| 7 | 196 | 0.21363 | -58.5 | 青野 |
| 8 | 104 | 0.22574 | -54.1 | 岡田 |
| 9 | 81 | 0.22750 | -53.7 | 松田 |
| 10 | 78 | 0.20327 | -58.7 | 河合 |
異方性の単純梁(1次)と2次要素のサンドウィッチ梁(鋼材:等方性 木材:異方性 木材を鋼材で挟む)の比較
| メッシュ | 要素数 | 変位 | 相対誤差 | 測定者 |
| 0.7 | 155266 | 0.0861 | -13.0 | 関合 |
| 0.8 | 138453 | 0.08349 | -15.7 | 岡田 |
| 0.9 | 82766 | 0.083312 | -15.9 | 松田 |
| 1.2 | 32279 | 0.08357 | -15.6 | 青野 |
| 1.3 | 28343 | 0.083667 | -15.5 | 山口 |
| 1.4 | 23667 | 0.08368 | -15.5 | 山本 |
| 1.5 | 19958 | 0.083516 | -15.6 | 進藤 |
| 1.6 | 19451 | 0.086037 | -13.1 | 河合 |
| 1.8 | 10933 | 0.084021 | -15.1 | 山口 |
| 2 | 10764 | 0.083323 | -15.8 | 進藤 |
| 3 | 3618 | 0.083467 | -15.7 | 山本 |
| 4 | 1623 | 0.0852 | -13.9 | 関合 |
| 5 | 1007 | 0.083104 | -16.1 | 千代岡 |
| 6 | 842 | 0.0821 | -17.1 | 高井 |
| 7 | 554 | 0.08075 | -18.4 | 青野 |
| 8 | 289 | 0.079715 | -19.5 | 進藤 |
| 9 | 261 | 0.078427 | -20.8 | 松田 |
| 10 | 232 | 0.082495 | -16.7 | 河合 |
[m]単位でモデリングするときは,密度の単位はkg/m3を用いる。
GenerateVectorsは2Dの結果を可視化するときに適用するものらしい。(別に入れても問題ないなら忘れないために常に入れておいたほうが安全だと思う)
Normalmodesanimationrealは鉛直or水平の振動を見ることができるもの?
Normalmodesanimationcomplexは鉛直・水平振動を同時に起こせるもの?
POUTRE 梁(ビーム)
COQUE シェル
AXE_POUTRE ビーム軸
coq_pou このオプションにより、船体内に格子状の部品を梁状の部品と接続することが可能になります?(原文:This option makes it possible to connect a part with a grid in hull with a beam part.)
http://www-mdp.eng.cam.ac.uk/web/CD/engapps/aster_docs/UDocs-HTML/U44401i1/U44401i1.pdf.html#52(P52)
5/15~5/26 教育実習
5/29 研究再開
全角/半角の切り替えは、「無変換」(左手親指)でもできる
コピペは、左クリックで領域選択したら、スクロールボタンで貼り付け
単語選択は、ダブルクリックで可(トリプルクリックだと行選択)
初めての学会発表で東北支部(岩手大学)で発表したが、やっぱり質問対応が上手くいかない。 質問の意図が上手く汲み取れなくて違う回答をしたあとに質問内容を変えてもらってなんとか回答できるようになる。
相手の質問内容を上手く理解できるようになる必要がある。
また、他の人の発表が全然理解できなかったのでもっと理解できるよう幅広い知識と様々な試験方法を知っておく必要があると感じた。
1