![[PukiWiki]](image/pukiwiki.png "[PukiWiki]")
| 人 | 体積(mm\( ^3 \)) | たわみ(mm) | 無次元化比剛性 | 順位 |
| さ | 11588 | 0.1383 | 2.166\( \times 10^{-3} \) | |
| す | 11973 | 0.163913 | 1.769\( \times 10^{-3} \) | |
| わ | 8211.3 | 0.5811 | 7.277\( \times 10^{-4} \) | |
| お | 11683 | 5.2600 | 5.650\( \times 10^{-5} \) | |
| ナ | 11331 | 0.168316 | 1.0214\( \times 10^{-3} \) |
| 人 | FEM(mm) |
| さ | 0.415424 |
| す | 0.416464 |
| わ | 0.417315 |
| お | -0.7181015 |
| ナ | -0.7181015 |
| 人 | 長さ | 手計算(mm) | FEM(mm) |
| さ | 100 | 40.00 | 39.09 |
| す | 200 | 320.0 | 311.7 |
| な | 300 | 1080 | |
| わ | 400 | 2560 | 2508.84 |
| お | 500 | 5000 | 4790 |
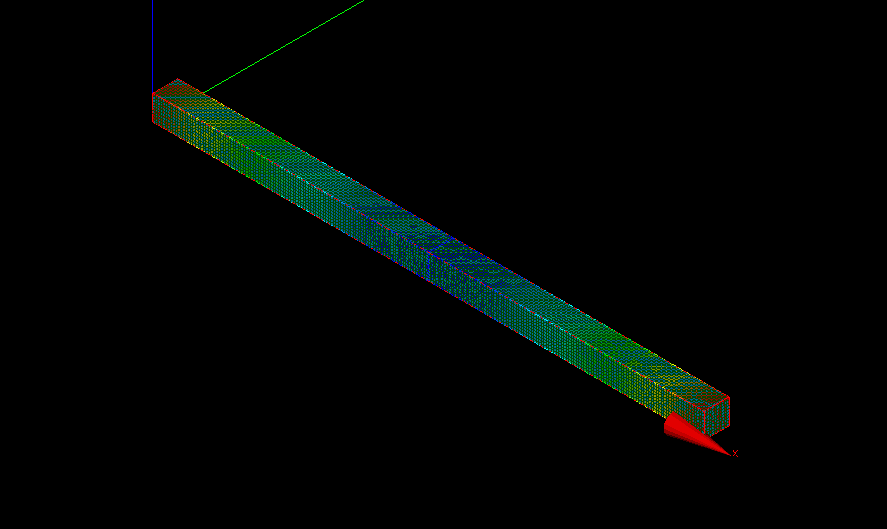長方形断面10mm*10mm*200mm(両端の張り出し10mmずつ)の単純梁中央載荷
| Length | FEM(mm) | \( \frac{P\ell^{3}}{48EI} \)(mm) | 相対誤差\( \frac{FEM-手}{手} \) |
| 0.8 | 3.27523 | 3.33333 | 1.743 |
黄緑の冊子の8-10ページに書いてます。
Create mesh→Assign a set of hypothesesを3D:Automatic Hexahedralizationを選択→Cancel→1Dを選択→AlgorithmをWire Discretisationを選択→HypothesisをLocal Lengthを選択し、Lengthは1mmとか2mmにする。→Apply and Close
単純な梁ならばこの方法で出来る。
しかし、複雑になると面が切れなくなってしまう。
Local Lengthを使うときは、６面体の領域に分割する必要がある。 試しにI形でmeshを切ってみる。
3Dプリンターの修理が間に合わず、年度内の3D造形はできませんでした。 すいません。
卒論発表が終わってから、2月中に、1位のモデルを３Dプリンタで印刷して サイカ試験してみるので、希望者は適宜参加する。
| 学生(いえき...） | 体積(mm\( ^3 \)) | たわみ(mm) | 剛性\( \frac{P\ell^{3}}{48v} \) | 比剛性（剛性/体積） | 要素数 |
| い | 7760 | 7.41 | 2811516 | 362 |
| え | 11448 | 5.729 | 3636469 | 317.7 | 180612 |
| き | 11736.458 | 3.539 | 5886735 | 501.6 | 107429 |
| け | 11717 | 3.20 | 6510417 | 556 | 51979 |
| さ | 11689.375415 | 2.22316 | 9371045.419 | 801.6720386 | 113954 |
| す | 11730 | 2.3182 | 8986857.619 | 766 | 89844 |
| ふ | 4720 | 9.96546 | 2090554.107 | 442.9 | 53882 |
| や | 11874.906223 | 6.17439 | 3374152.48 | 284.1414001 | 66611 |
以下の条件のモデルをSalomeで作成する。 FEM用の拘束線、載荷線を作っておく。 スパン100mmの単純支持境界条件と中央線載荷の荷重条件を入れて、 Salome-Mecaで解く。
| Length | 変位(mm) |
| 12 | 0.188698 |
| 11 | 0.211159 |
| 10 | 0.211158 |
| 9 | 0.296500 |
| 8 | 0.300116 |
| 7 | 0.311889 |
| 6 | 0.276896 |
| 5 | 0.291271 |
| スパン(mm) | FEM変位(mm) | \( \frac{P\ell^{3}}{48EI} \) |
| 110 | 0.551006 | 0.554583 |
| 120 | 0.715056 | 0.720000 |
| 130 | 0.911506 | 0.915417 |
| 140 | 1.13605 | 1.143333 |
| 150 | 1.39896 | 1.406250 |
| 160 | 1.69264 | 1.706667 |
| 170 | 2.02416 | 2.047083 |
| 180 | 2.39042 | 2.430000 |
| 日付 | 欠席者 | 内容 |
| 10/23 | なし | テキストファイル、バイナリファイル、Unixコマンド、vi |
| 10/16 | なし | Linuxの話、タッチタイプの練習 |
| 10/9 | なし | viの使い方、日本語入力 |
以下の条件のモデルをSalomeで作成する。 FEM用の拘束線、載荷線を作っておく。 メッシュの細かさは後で指定するが、unvc3d4tan.f90を使って、 スパン100mmの単純支持境界条件と中央線載荷の荷重条件を入れて、 CalculiXで解いてみる。
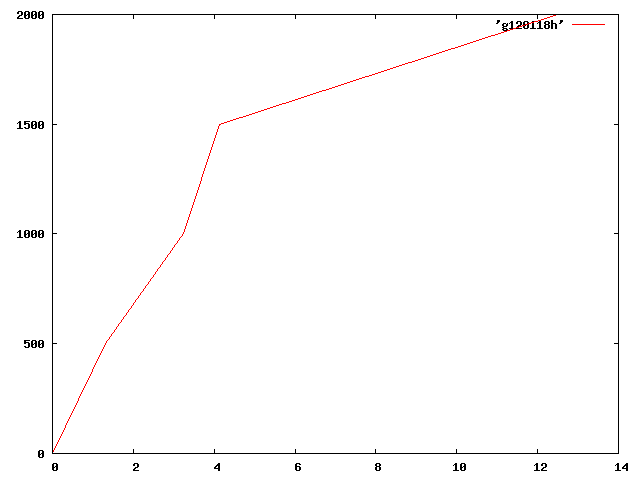
す2回目 0. 0. 0.02 0.505 0.06 1.505 0.09 2.505 0.12 3.505 0.15 4.505 0.18 5.505 0.21 6.505 0.24 7.505 0.28 8.505 0.31 9.505 0.34 10.505 0.37 11.505 0.40 12.505 0.43 13.505 0.46 14.505
き1回目 0. 0. 0.05 0.505 0.10 1.505 0.15 2.505 0.21 3.505 0.26 4.505 0.31 5.505 0.37 6.505 0.43 7.505 0.49 8.505 0.55 9.505 0.61 10.505 0.66 11.505 0.71 12.505 0.77 13.505
き2回目 0. 0. 0.11 0.505 0.17 1.505 0.23 2.505 0.28 3.505 0.34 4.505 0.40 5.505 0.46 6.505 0.51 7.505 0.56 8.505 0.61 9.505 0.65 10.505 0.70 11.505 0.75 12.505 0.80 13.505
implicit real*8(a-h,o-z) print*,'2GPaのときの剛性を入れて' read*, ei print*,'最大荷重を入れて' read*,p p=p*9.8 print*, '最大変位を入れて' read*, vmax ei=ei/2.*2.84 v=p/48./ei*(3.*100**2*45.-4.*45.**3) print*,'たわみは',v gousei=p/48./vmax*(3.*100**2*45.-4.*45.**3) print*, '剛性は', gousei end
単純梁中央載荷のたわみ \( v(z)=\frac{P}{48EI}(3\ell^{2}z-4z^{3}) \) \( (0\le z\le\frac{\ell}{2}) \)
つまり、実験で中央載荷して、z=45mmのたわみを測定したならば、 実験で測定された剛性は \( $EI_{実験}=\frac{P(3\ell^{2}z-4z^{3})}{48v_{実験}} \)$にz=45mmを代入
鈴木
| たわみmm | 要素数 |
| 1.472 | 4627 |
| 1.528 | 6005 |
| 1.526 | 10703 |
| 1.565 | 20078 |
| 1.639 | 90489 |
| 2.057 | 150514 |
| 1.685 | 277913 |
| 学生(いすた...） | 体積(mm\( ^3 \)) | たわみ(mm) | 剛性\( \frac{P\ell^{3}}{48v} \) | 比剛性（剛性/体積） | 要素数 |
| た | 11070 | 4.56 | 4568713 | 413 | 99071 |
| す | 11778 | 2.33 | 8941345 | 759 | 90489 |
| い | 10993 | 7.346 | 2836010 | 258.0 | 333821 |
| き | 11933 | 3.350 | 6217050 | 521 | 146060 |
| こ | 11159 | 28.8 | 813704 | 73 | 238754 |
| じ | 11872 | 6.65 | 3132653 | 264 | 14151 |
| や | 11744 | 6.83 | 3054740 | 260 | 183279 |
○計算結果
理論値：62.1mm (メッシュで比較)
| 幅（x) | 高さ(y) | 長さ(z) | メッシュ | 要素数 | dat(mm) | 手(mm) | FEM/理論 | 相対誤差(%) |
| 10 | 10 | 1000 | 1 | 462452 | 60.3 | 62 | 0.972 | -2.9 |
| 10 | 10 | 1000 | 3 | 37717 | 51.3 | 62 | 0.827 | -17.4 |
| 10 | 10 | 1000 | 5 | 16414 | 48 | 62 | 0.774 | -22.7 |
| 10 | 10 | 1000 | 10 | 4512 | 33.3 | 62 | 0.537 | -46.4 |
| 10 | 10 | 1000 | 20 | 862 | 8.77 | 62 | 0.141 | -85.9 |
| 10 | 10 | 1000 | 101の1/10 | 34 | 62 | 0.548 | |
| 10 | 10 | 1000 | 101 | 0.4 | 62 | 0.45*10^-4 | |
| 10 | 10 | 1000 | 101の3倍 | 81*10^-9 | 62 | 1.3*10^-9 |
(体積一定で形状比較)
| 幅（x) | 高さ(y) | 長さ(z) | メッシュ | dat(mm) | 手(mm) | 相対誤差 |
| 10 | 20 | 1000 | 10 | 6.459 | 7.767 | 0.832 |
| 20 | 10 | 1000 | 10 | 13.11 | 31.07 | 0.422 |
(体積を変えて比較)
| 幅（x) | 高さ(y) | 長さ(z) | メッシュ | dat(mm) | 手(mm) | 相対誤差 |
| 20 | 20 | 1000 | 10 | 3.078 | 3.8835 | 0.793 |
| 30 | 30 | 1000 | 10 | 0.67 | 0.76 | 0.882 |
| 幅 | 高さ | 長さ | FEM/手計算 | メッシュ |
| 10 | 10 | 100 | 0.973 | 1(<-10.09) |
| 10 | 30 | 1000 | 0.864 | そのまま |
| 15 | 15 | 1000 | 0.782 | 7 |
| 20 | 20 | 1000 | 0.788 | 5 |
| 30 | 30 | 1000 | 0.852 | 10(<-42) |
| 40 | 40 | 1000 | 0.961 | 5(<-100) |
| 100 | 200 | 1000 | 0.801 | 102.47そのまま |
| 100 | 200 | 1000 | 1.02 | 10.47(<-102.47) |
| メッシュ長さ | 計算結果 |
| 41.275 | 9290070 |
| 31.275 | 9302012 |
| 21.275 | 9389625 |
| 電卓での計算結果 | 9424777 |
| メッシュ長さ | 計算結果 |
| 41.814 | 3054424 |
| 13.938 | 3122485 |
| 電卓での計算結果 | 3141592 |
| メッシュ長さ | 計算結果 |
| 34.78886 | 4048687 |
| 25 | 4152818 |
| 17 | 4154875 |
| 10 | 4180501 |
| 5 | 4186770 |
| 電卓での計算結果 | 4188790 |
各自1橋ずつ制作。できた人から載荷試験。 優秀者に粗品があるかも（未定）。
トラス再挑戦。対傾構をちゃんといれて。接合部はしっかりと丁寧に。
すいスティックを部材としたトラス橋を作ってみる。 去年のトラスを参考に（対傾向を入れて、載荷部分を補強するなど）去年の モデルの弱点を改善する。
丸スティック、三角スティック、逆三角スティック、四角スティック、ギザギザ折りスティックを５本ずつ作って、次回、曲げ試験を行なって、剛性・強度比較する。
すいガールズ橋と同様のすいスティック方式の橋と、三角スティック橋とを作って、 次週に載荷試験してみる。
去年の例(学内のみ）等を見ながら、 より剛性・強度の高い橋を作るにはどうすればいいか、各自のアイデアを考えてきて、紹介してもらう。
| 10/4 | 全員 |
| 10/11 | 全員 |
| 10/18 | 全員 |
| 11/1 | 全員 |
| 11/8 | 全員 |
| 11/15 | 全員 |
| 11/22 | 全員 |
| 11/29 | 全員 |
| 12/13 | 全員 |
| 12/20 | 全員 |
| 1/10 | 全員 |
| Yさん試作 | 9.5kgf | プラットトラスタイプ |
| Oさん試作 | 13.0kgf | ハウトラスタイプ |
| Nさん試作 | 24.5kgf | キングポストトラスタイプ |
| Kさん試作 | 34.0kgf | キングポストトラスタイプ |
| Sさん試作 | 19.5kgf | スイスティック板2段離間タイプ |
| Tさん試作 | 19.5kgf | スイスティック巻きタイプ |
| Iさん試作 | 34kgf | 1分程度で破壊 |
暫定1位 主要な桁部分はスイスティック3本の三角形の上側1本に、 載荷用の掛けひもを引っ掛けるためのもう1本のすいスティックを主桁より短めに 巻いている。掛け紐は、すいスティックで作った輪を折り曲げたV字型で、 主桁の両脇から1割ぐらいのところに引っ掛ける。 載荷用手下げ袋は、掛け紐の輪のV字型の折れ曲がった箇所に通す。 掛け紐には引張がかかるので、紙2枚程度の細いすいスティックでも十分に耐える。 主桁への載荷は、両脇の当曲げと、上部の引っ掛け用短めスティックへの圧縮が作用する。主桁中央での載荷ではないので、主桁中央は折れ曲がらず、 V字方向への圧縮が作用する掛け紐の引っ掛け部が、少しずつめり込んでいくものの、 材料的な耐力を失っている箇所は、20kgf以上でも特に認められない。 最終的な破壊は、34kgf載荷時に一方の掛け紐の引っ掛け部が、クリープにより徐々に 折れ曲がって1分程度で落橋。
| Sさん試作 | 18.5kgf |
暫定1位
スイスティックを横に並べた板2段の間に短いスイスティックのスペーサーを挟んで上下に離して固定し、桁高をかせぐ。
| プラットトラスタイプ | 8kgf |
| ハウトラス？タイプ | 7kgf |
| すいガールタイプ | 17.1kgf |
| 三角スティックタイプ | 16.1kgf |
| 種類 | 1回目 | 2回目 | 3回目 | 4回目 | 5回目 | 平均 |
| まる棒スティック | 968gf | 597gf | 694gf | 888gf | 679gf | 765.2gf |
| 三角スティック | 194gf | 449gf | 611gf | 645gf | 428gf | 465.4gf |
| 逆三角スティック | 472gf | 588 | 508gf | 291gf | 451gf | 462gf |
| 四角スティック | 291gf | 514gf | 571gf | 468gf | 588gf | 486.4gf |
崩壊荷重18.5kgf以上を目標に各自で橋を試作。 定規、鉛筆は使ってよい。 糊も制限はしないが、使った量を申告する。 できた人から実験する。 期間内なら何回挑戦してもよい。 毎週、顔合わせをして、進捗状況を確認する。 1月中には全員の実験が終了し、 レポートに着手できるようにする。 その時点で、実験の写真はここに公開する。
| アーチ系 | 斎 |
| トラス系 | 長星 |
| プレートガーダー系 | 渡鴨 |
2主桁の合理化橋的な構造で、主桁も横桁も6枚から8枚でごっつく、 糊も全面につけてしっかり固定する。
紙を4から8枚貼り合わせてケント紙並の剛性を有すI桁や横構を作って貼り合わせ、 ケント紙では剛性を発揮できているプレートガーダー的な構造を試しに作ってみる。 東大生チームが意図した桁高をかせいで断面二次を確保するという戦略に沿った橋は作れないか。
| 10/12までの課題 | すいガールズ方式の橋を試作してみる |
| 10/19までの課題 | すいガールズ方式の橋の作り直し |
| 名 | 崩壊荷重 |
| 星 | 8.5kgf |
| 渡 | 6kgf | |
| 長 | 4kgf | |
| 鴨 | 9kgf | |
| 斎 | 20kgf |
すいガールと同様のすいスティック方式の橋を作ったが、 15枚で15本のスティックを作ろうとすると、他の部分に割ける紙が 少なくなり、正方形からスティックを作ったところ、橋長が短くなり、 十分な強度を発揮できなかった。 10kgf
A4用紙の7枚のみを幅をせまく切り、切り出した細長い部分で、 スティック3本を巻く紙、三角桁全体を巻く紙に割く。 19.5kgf.我々のコピー用紙とスティック糊でもすいガールズと同等以上の強度を確保できることがわかった。
4主桁I型プレートガーダー。 フランジなども2枚程度の補剛で糊も全面にはついておらず剛性不足の割に 桁高も高く簡単に局部座屈というか初期不整がそのまま拡大。 4kgf.
2主桁プレートガーダー。 3箇所の対傾構は、天板、底板と接着されていない。 横構はすいスティックで☓字に。 フランジの張り出しは長め。 垂直、水平補剛材はなし。 載荷部がめり込み、桁中央ウェブ部に局部座屈が発生して崩壊。 7kgf?
2主桁のプレートガーダー。使用した糊は2.5本。 3箇所の対傾構は、天板、底板と接着。 ウェブ中央部に垂直補剛材（これも天板、底板に接着）。 前回のように中央部がめりこむことはなく、 比較的剛性を保つ。 支点側が相対的に剛性が低く、補剛材もないため、 支点付近のウェブから局部座屈が始まる。 最終的には、(1/4点より)支点側に近い部位で天板がめり込み、 そこで折れ曲がって崩壊。 内部の×字のすいスティックは、細めだったため、 引っ張りにも圧縮にも抵抗していないよう。 18.5kgf
| 日付 | 出席者(場所) | 作業内容 |
| 10/05 | 鴨斎長星渡(218) | 打ち合わせ |
| 10/12 | 鴨斎長星渡(218) | 予備実験 |
| 10/19 | 鴨斎長星渡(218) | 実験 |
| 11/2 | 鴨斎長星渡(218) | 実験 |
| 11/9 | 鴨斎長星渡(218) | 実験 |
すイエんサーでは、すいガールズチームはぐるぐる巻にした棒を3本ずつ束ねて 並べていた一方、東大生チームは、長方形断面にすることで断面二次モーメントを 確保しようとしていた。もちろん、断面二次についていえば、円管よりも （縦長）長方形断面の方が圧倒的に大きいから、東大生チームの設計思想の方が、 効率的に断面二次をかせいで有利に思われた。しかし、実際に実験してみると、 東大生チームの橋は途中で横倒れしてしまい、すいガールズチームの円管の梁の 数分の一の荷重にしか耐えられなかった。
番組では、すいガールズチームの勝ちということで終わってしまい、 「紙のような極めて薄肉の構造では、下手に断面二次をかせごうとするよりも、 まずは、ぐるぐる巻など圧肉化して、局部座屈や全体座屈の発生をふせぎ、 円管の屈服で破壊するような構造にした方がまし」 ということなのか、 「薄い紙であっても、適切に座屈や転倒をふせぎながら断面二次をかせぐ 構造はありうる（東大生チームの設計もちょっと変えれば、遥かに強くなる）」 ということなのか、その辺の検証が全くなされないので、 気持ち悪い。
ちなみに、もう少し厚いケント紙とかであれば、 構造力学的に有利と予想されるプレートガーダーや桁橋はちゃんと予想通りに強くなる （&link(2003年度の創造工房,http://www.str.ce.akita-u.ac.jp/~gotou/souzou/#por03)
ケント紙の二十壁構造で、ハニカム構造、それを引張切った互い違い格子桁、 普通の格子桁の三種を試作してみる。 おおきさは、桁高が15-20mm, 桁幅が100-150mm, 桁長が400-600mm程度。 ハニカムや互い違い格子は、剛性の高い方を桁長方向にする。
| 日付 | 出席者(場所) | 作業内容 |
| 10/05 | A/E/K/N/S(218) | 打ち合わせ |
| 10/12 | A/E/K/N/S(218) | 文献調査、作業計画 |
| 10/19 | A/E/N/S(218) | 製作方法の検討 |
| 10/25 | A/E/K/N/S(218) | 製作方法の検討 |
| 11/2 | A/E/K/N/S(218) | 製作モデルの検討 |
| 11/2 | A/E/K/N/S(218) | 製作方法の検討 |
| 11/9 | A/E/K/N/S(218) | 予備試験 |
| 11/30 | A/E/K/N/S(218) | 実験 |
| 12/7 | A/E/K/N(218) | 実験 |
| 12/14 | A/E/K/N/S(218) | 実験 |
"honeycomb frp deck bridge"
年内に、アクリル床版+グルーガン仕様で、半円筒と半ダイヤカット円筒の 試験体を作成し、載荷試験を行う。 年明けに、ダイヤカットのパターン数を5*10とかに変更したモデルを作成して 載荷試験を行う。
| 日付 | 出席者(場所) | 作業内容 |
| 10/06 | U/K/N/Y(218) | 打ち合わせ |
| 10/13 | U/K/N/Y(218) | 半円筒の作成計画 |
今回の創造工房では、ダイヤカットの構造物の利用というテーマで実験を行った。そのために、ダイヤカットの柱の曲げ強度試験を行った。その結果、強度は、円柱の二分の一から四分の一となってしまった。このような結果となってしまった理由として断面二次モーメントの低下が考えられる。また、また、実験中にも飛び移り座屈により急激に断面が低下して結果として断面二次モーメントの低下が起こった。これにより、載荷点における応力が増加し円柱より強度が低下したと考えられる。また、ダイアカットの構造物を現場で作るには施工が難しいという問題もある。しかし、円柱に比べてメリットがあることも分かった。それは、円柱は、壊れる際に急激に破壊したが、ダイアカットにする事によってゆっくりとこわれていった。これは円柱より延性が高いということなので構造物として利用するには危険性が少なくなるのでとてもよい特性だと考えられる。
実験前の予想では、ダイヤカット構造のほうが耐久力に優れていると思ったが、実験をした結果、円筒のほうが曲げ強度が優れているということが分かった。氷結に代表される缶チューハイに用いられているダイヤカット構造であるが、内部からの圧力には強い半面、外部からの曲げにはさほど耐久力がないことが、実験結果からも分かった。これは、ダイヤカット構造の他におりの部分に曲げモーメントが集中した結果と考える。私の知識不足・調査が足りないだけかもしれないが、実際の建築物にダイヤカット構造が使用されないのは、このあたりに原因があるのだと私は考える。しかし、授業の最後で後藤先生がおっしゃっていた「災害時の際の橋梁への利用」も、補強材の使用・材質の選考・使用部位の考慮をすれば十分可能と思われる。（橋梁本体でなく、それを覆う屋根としての使用など）
ダイヤカット型円筒を橋などに利用できるか>
- 模型製作について
- より精度の高い実験結果を得るための工夫
- ケント紙に折り目をつける際は、ノミを使用
- のりしろは実験に影響が出ないように２～３�程度にとる
- 小さいと接着時に円筒に手が入らないので、出来るだけ大きくとって作製する
- 接着部は斜めに
など。。。
結果はダイヤカット型円筒よりも普通の円筒の方が曲げに対する強度が高かった。 ダイヤカット型円筒は荷重を載せていくと、だんだんと変形していき最後には、潰れるように破壊した。 円筒は破壊するまでは変形は小さかったが、荷重に耐えられなくなると急激に破壊した。 曲げに対してはダイヤカット型円筒よりも円筒の方が、強度があったがダイヤカット型円筒には延性があることが実験結果より得られた。
実験を行う前はダイヤカットの方が円筒よりも強度があると予測していた。 なぜならダイヤカットは缶コーヒーや缶チューハイに使われており、わざわざそのように加工するのだから、強度が高くなるとかメリットがあるだろうと思ったからだ。 しかし実験結果は違った。では、ダイヤカットのメリットとは何だろう。調べてみると、ダイヤカットはもともと宇宙研究で考案され、強度を保ちながら、材料を出来るだけ軽量化するためのもので、曲げに対する耐力ではなく、内圧に対する耐力に優れているものであった。 曲げに対する強度は、円筒より劣っているダイヤカット型円筒だが、軽量化が可能、延性があることなどから、内部に補強材を入れるなどして強度を持たせ、災害時、可動式の橋梁としてなどの利用方法があるのではないかと思う。
今回、「ダイヤカットの構造物を橋などに利用できないか」というテーマで実験を行った。しかし、結論から言って「非現実的」と考えられる。その根拠としては、今回の「ケント紙を用いた模擬荷重試験」の実験結果が示している。一回目（6×12、等間隔）の結果、二回目（6×12、間隔にバラつきを持たせたもの）の結果の二つと円柱の結果を比べると、円柱の方が2～4倍近い荷重に耐えられるという結果となった。よって、ダイヤカットにしない方が鉛直方向に対する強度に優れていることが分かる。もちろん今回は六角形のものしか荷重試験を行っていないので、「ダイヤカットにする」＝「必ず鉛直方向の強度の低下」とはいえない。しかし、六角形のダイヤカットにすることで強度が円柱に比べて各段に落ちている。このことからダイヤカットの形を変えてもそこまで強度があがるとは考えられない。結果「ダイヤカットの構造物は橋などの構造物には不向き」と言える。原因として、第一に断面二次の低下があると考えられる。ダイヤカットの断面積の方が円柱の断面積よりも小さくなること、飛び移り座屈により急激な断面積の低下などが考えられる。第二にダイヤカットにすることによって折り目がつき、壊れやすくなることも考えられる。ダイヤカットにすることで施工が難しい点、強度が下がる点を考慮すると構造物としての利用価値は格段に落ちると考える。強いてメリットを挙げるなら第一に円柱は一気に破壊されたが、ダイヤカットは初めの局部座屈から破壊までのスパンが少しあった点。第二に設計での景観のバリエーションが増える点の二つが考えられる。延性の特性を生かして内部、外部を補強することも考えられるが、やはり、強度を格段に下げてまでダイヤカット構造物を利用するメリットが小さ過ぎると考える。ならば、円柱構造物に延性を持たせる工夫を考えたほうが利口ではないかと考える。（現実可能かは分からないが）
今回、ダイヤカットの構造物への利用というテーマで、ダイヤカット柱と円柱の曲げ強度試験を行い曲げに対する強度について比較した。実験結果のグラフより、ダイヤカット柱は2回とも円柱よりも低い値となった。今回の実験では、製作者の作業精度により実験値に最大５割弱の誤差が生じたが、ダイヤカット柱の曲げ強度は円柱の1/2.5から1/4程度となったので曲げに対して円柱より劣るであろうことが分かる。この理由としてダイヤカットの折り目によって荷重が上手く分散・伝達されずに部分的に集中してしまうため、局部座屈が生じ低強度となったのではないかと考えられる。しかし、円柱は座屈が生じてから破壊に至るまでの状態の変化が急激であったのに対して、ダイヤカット柱は局部座屈が生じてから破壊に至るまで延性があることがグラフからも読みとれる。この特性を利用し、ダイヤカット柱の内側から対傾構のようなもので補強したり、任意の場所から局部座屈を生じさせるような構造にすれば、延性を利用して十分構造物として利用可能ではないかと思う。
&link(新しいタイプの屋根付き橋,http://www.str.ce.akita-u.ac.jp/~gotou/linux/tizai.html#yane)を ダイヤカット型円筒とかで作ってみたらどうなるだろうかの予備試験。
前回の課題はうまくできなかったようなので、まずは A3のコピー用紙の短辺を1辺とする正方形の半分の長方形を 細長く丸めた6角、8角のダイヤカットを作ってみる。 のりしろは、長方形の対角線方向にダイヤカットの斜め線に沿って 切り込んでいく。長方形の対角線とダイヤカットの斜め線は一致しないので、 「2個斜めに進んで1個横に戻る」みたいなギザギザになる。
| 日付 | 場所 | 出席者 | 内容 |
| 10/14 | 218 | I/K/T/H/U | ガイダンス |
| 10/21 | 218 | I/T/H/U | 進捗確認、課題 |
| 10/28 | 218 | I/K/T/H/U | 進捗確認、課題 |
| 11/4 | 218 | I/K/T/H | 進捗確認、課題 |
| 11/11 | 218 | I/K/T/H/U | 進捗確認、課題 |
| 11/25 | 218 | I/K/T/H/U | 実験 |
| 12/9 | 218 | I/K/T/H/U | 実験 |
| 12/16 | 218 | I/K/T/H/U | レポートの説明 |
以下は2008年度の残骸など
2008年の授業は12/17が最後。 2009年は1/14から。折り畳み円筒の引っ張り試験。
| 日付 | 出席者(場所) | 作業内容 |
| 10/01 | H/E/S/Y(218) | 打ち合わせ |
| 10/15 | H/E/S/Y(218) | 打ち合わせ |
| 10/22 | H/E/S/Y(218) | 打ち合わせ |
| 10/29 | H/E/S/Y(218) | 打ち合わせ |
| 11/5 | H/E/S(218) | 打ち合わせ |
| 11/12 | E/Y(218) | 打ち合わせ |
| 11/19 | H/E/S/Y(218) | 実験 |
| 11/26 | H/E/S/Y(218) | 実験 |
| 12/3 | H/E/Y(218) | 実験 |
| 12/10 | H/E/S/Y(218) | 実験 |
| 12/17 | E/S/Y(218) | 装置製作 |
| 1/14 | H/E/S/Y(218) | 実験 |
| B3 | B2008 | KN-528 |
| A3 | A1504 | KN-514 |
| A4 | A1508 | KN-518 |
){kind=link}
,){kind=link}
)と同じように6*12パターンをA3コピー用紙で製作){kind=link}