田村の卒論日誌

\( v=\frac{P\ell^{3}}{48EI} \)

卒業研究「木材を用いたハイブリッド梁の数値的基礎解析」†

2✕6ハイブリッド材の弾塑性解析(elastoplastic analysis)[後に節を考慮]†

• 解析手法
• 
• 解析モデル
• 

  スパン長2000mm、2✕6材を想定して断面140mm✕114mm、鋼材を2本入れるモデルと4本入れるモデルでそれぞれ鋼材直径10mmと20mmの条件で解析を行う

• 設定した応力ひずみ曲線(stress-strain curve)
• 
• 木材のみの解析結果
• 
• 鋼材入りの解析結果
• 
• 

載荷試験†

• 今まで使っていた載荷試験機の限界荷重50kNでも試験体を破壊することができなかったためより荷重をかけれる試験機を整備
• 
• まだうまく動かせるかわからないので試験機の情報収集と予備試験を行った後中断している実験の再開
• 
• 
• 
• 
• 

試験結果†

• 
• 
• 

破壊後写真†

• 
• 
• 

アラミド引張試験†

• 
• A ・B ・C
• ・ ・
• 

メモ†

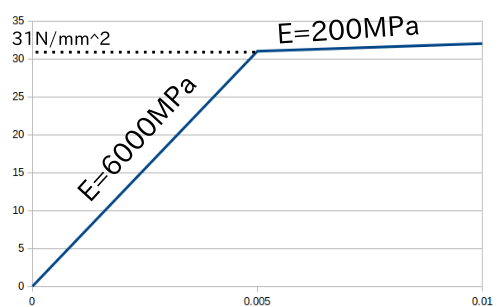
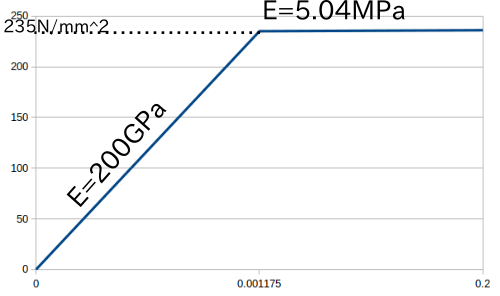
• 木材工学発表後想定するツーバイ材の材料定数を指摘されたので、弾性係数6GPa→10GPa、降伏点31MPa→90MPaに直して再計算（引張強度90MPa,圧縮強度40MPa）

弾塑性エラー†

• 
• 

salome 弾塑性（引張）†

• https://www.slideshare.net/stebee19/salomemeca-59878666
• 応力についてhttps://d-monoweb.com/blog/evaluate-strength-mises-stress/

直交異方性弾塑性解析 2022/9/30〜†

• salomeで異方性を考慮した弾塑性解析ができないか
• http://www.str.ce.akita-u.ac.jp/~gotouhan/j2022/tamura/hill.comm
• http://www.str.ce.akita-u.ac.jp/~gotouhan/j2022/tamura/hill_IS_z.hdf
• 

2022/11/25
「F1_A,C_A,F1_M」とかに0を入力して計算は回ったのでF_MXX_XXとかC_MXY_XYの値を変えて解析結果に違いが出るか確認したところほぼ変化なかった
→F1_A,C_A,F1_Mとかの値を変えて計算してた時は解析結果に違いがあったのでそこに設定するべき値を調査する
　＆コンター図に違和感があったので弾塑性解析ができているか確認

＊META_LEMA_ANIのLEMAがおそらくLemaitreモデルのことではないかと思われる→そこらへんを調べてF1_A,C_A,F1_Mとかに入れるべき値を見つけられないか

• META_LEMA_ANI例題

2022/11/16
META_LEMA_ANIのパラメータ設定の下部にマトリクスの値を設定するであろう場所を発見し、今まで設定していた「F1_A,C_A,F1_M」とかがまた違う値を設定するところであったと思われる。
＊ここのパラメータを設定する際のFとCの違いはcold-faceとhot-faceの違いであった。「cold=froid[フランス語],hot=chaud[フランス語]」　今のところFとCには同じ値を設定する

とりあえず今まで設定していたパラメータに0を入力してF_MXX_XXとかC_MXY_XYとかに適当に値を入れて計算が回るか確認する

2022/10/4〜
簡単な直方体モデルを作成し、salomで異方性パラメータを入れるMETA_LEMA_ANI(Define a materialの中)にcode-asterのマニュアルにのってる等方性にする設定で解析したものと今までの方法で等方性解析したものを比べてみた
解析がまわったので結果を比べてみたところ全く同じ結果で設定が反映されてるのか分からなかったため異方性パラメータの値をを少し変えて再計算した(*詳しく結果を確認したら微妙な違いが確認できた)
下のようなエラーが出たのでアドバイスどおりにAnalysis設定上のRESI_GLOB_RELAの値を0.0001だったものを0.001にしたところ計算がまわった
等方性の時とは解析結果に違いが出たので異方性パラメータの設定は反映されてることがわかった
異方性パラメータに設定する値を木材のものに近づけるように調査中...

• 

  2022/10/3 
  AnsysのHillの異方性パラメータに関するページとCode-Asterの材料設定に関するガイドページからHillの異方性パラメータを設定すると思われるところを発見
  2つのページを比べるとsalome上で設定するべき値が分かりそうだが、各軸方向の降伏応力と降伏せん断応力が必要になる？

• https://www.cybernet.co.jp/ansys/product/lineup/multiscale/relation/mono009.html
• https://www.code-aster.org/doc/default/en/man_u/u4/u4.43.01.pdf (p.137〜)

  2022/9/30
  Hillの降伏条件という直交異方性を考慮した弾塑性解析に必要なパラメータを設定するところがないor見つけられてない→Hillの降伏条件や直交異方性弾塑性について文献調査↓

• https://www.jstage.jst.go.jp/article/aijs/79/700/79_741/_pdf
• https://archi.hiro.kindai.ac.jp/laboratory/SAL/study/ronbun/2018/nagaoka.pdf
• http://www.opencae.or.jp/wp-content/uploads/2019/12/08-non_linear_capabilities.pdf
• https://www.jstage.jst.go.jp/article/jilm/65/5/65_164/_pdf

• 後藤メモ221110

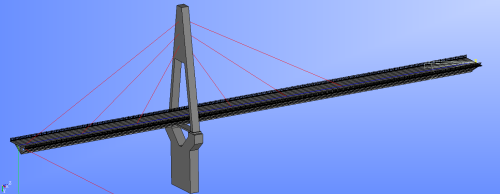
新橋の考案†

・都会の町並みに合う歩道橋（斜張橋）

• 4/18~ 基礎部分を足４本と基礎上部に分けて印刷
• 4/11~ 基礎部分のモデリングができたのでCuraでgcodeに変換後印刷
• 4/5~ 主塔モデル２の基礎部分の作り込みと３Ｄプリンターでの印刷
• R4↑
• 11/8~　一旦考えたデザインをsalome上でモデリングする 「今後の目標」

  ・新橋全体のデザインを考えていく
  ・ハイブリッド建材に関して鋼材の本数や太さを変えた時の曲げ、圧縮、座屈の解析を行う

• 11/1~　主塔に注目してデザインを考えていく
• 10/25~　理想とする橋の簡易的なモデルが完成したので、強度や重量を計算しながら断面形状や構造を調整していく
  木歩道橋に関する資料
• 10/18~　主桁と高欄のモデル作成（第１モデル完成）
• 10/11~　見た目でどんな感じか確かめるために何パターンかSalome上で簡単にモデリングしてみる
• R3↑

3Dプリンター†

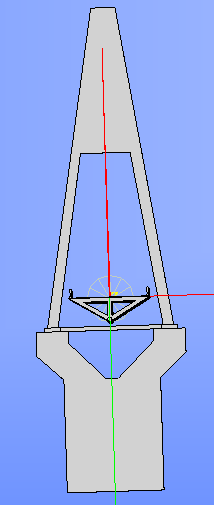
主塔モデル2†

・トラス構造で高さを出す構造として鉄塔に注目
・主塔モデル1から基礎部の安定感を出すために錐形に→エッフェル塔を参考にデザイン

• 
• 
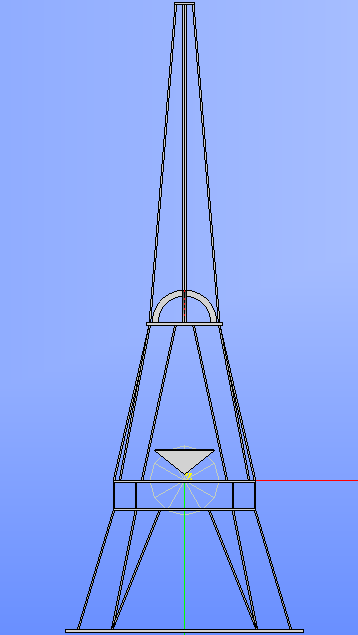
• 大体の外形ができた途中経過、この後斜材を付けていく→部材数が多くなり不朽の観点から難あり

主塔モデル1†

モデル1で採用したA型のまま木材もしくはハイブリッド建材でトラス構造のようなデザインに

• 
• 

  最大部材長7m←実際この長さの部材は難しい...
  全体的に不安定な感じがある+そのまま基礎部も木材で作ったらさらに不安定感が出る

モデル１†

• 
• 

  諸元
  [スパン]60m+105m,[幅員]10m
  [材料]木材又は木材と鋼材の複合部材
  [主桁]トラス状(キングポストトラス)
  [塔]A型もしくは逆Y型
  [ケーブル]1面ファン状3段→歩道橋のため景観を重視

・橋長や幅員、塔の高さ位置などは奥和歌大橋を参考にモデリング

ハイブリッド部材の解析†

考案中の新橋モデルに取り入れるハイブリッド部材の強度解析

• https://www.icba.or.jp/kenchikuhorei/2018tsuiho/505_523_9.1.pdf
• https://www.ffpri.affrc.go.jp/labs/etj/karube/Mokkyo/pdf/20000927JTE42.KaketudukeruJidai.pdf

• 1/17~　2×8材での解析も行い比較対象を増やして、強度,重量,値段について照査する
• 応力のまとめ方を縁応力をみてまとめる→2×4と2×6での挙動の違いがなくなった
• 2✕材を用いた鋼-木ハイブリッド部材の曲げ、圧縮、座屈解析を行う
• http://zenmoku-data.jp/pdf/report-03-3.pdf
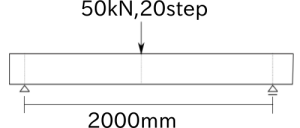
• 取り掛かりとして2✕6材（断面38✕140）の使用を想定して、2✕6を3枚重ねてその間に丸鋼を入れたようなモデルを作成
• 12/6~　2✕4材、2✕6材、2✕8材それぞれに関して丸鋼の直径を10mm~20mmまで2mmずつ変化させた時の解析を行って剛性評価を行う

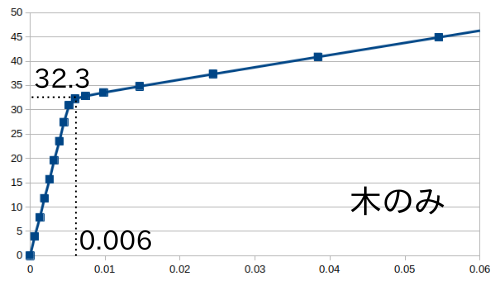
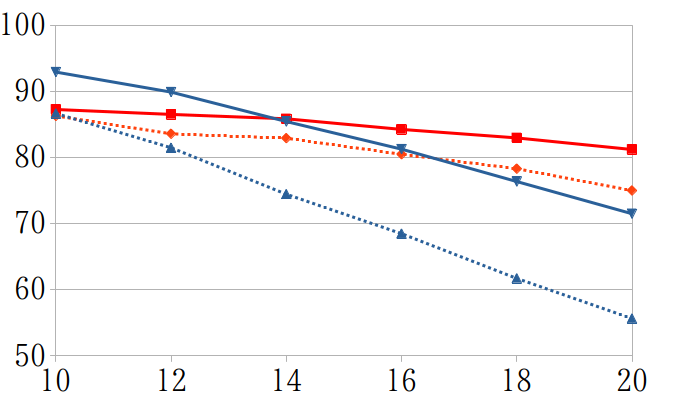
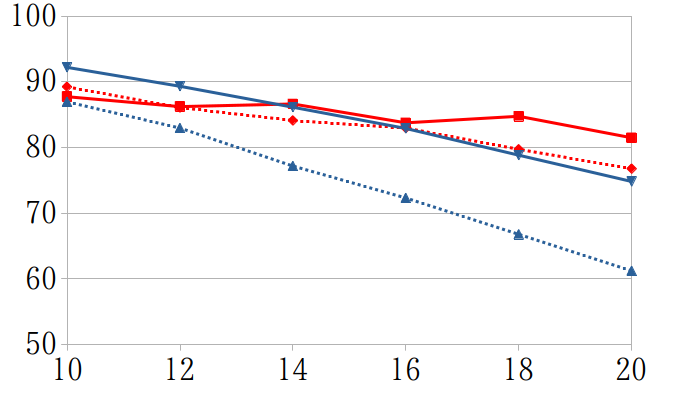
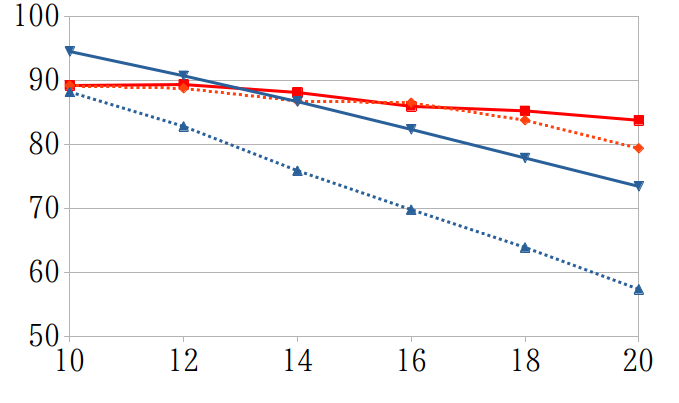
2×4と2×6の曲げ解析結果(東北支部2022)†

鋼材直径とたわみ量、鋼材直径と載荷断面上縁と下縁の直応力のグラフ

• 
• 
• 

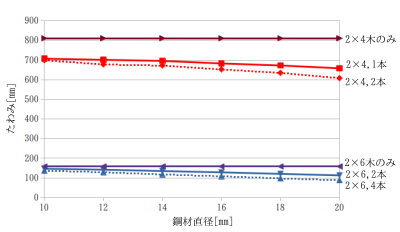
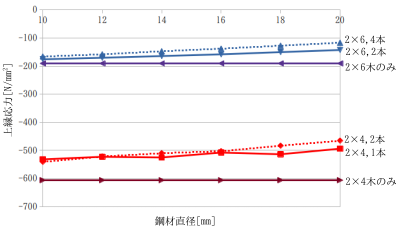
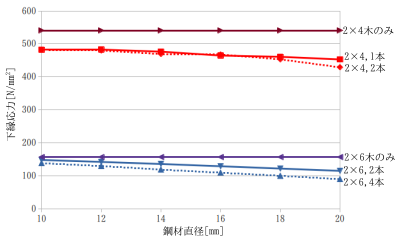
  木材のみに対する値をプロットしたグラフ

• たわみ
• 上縁
• 下縁

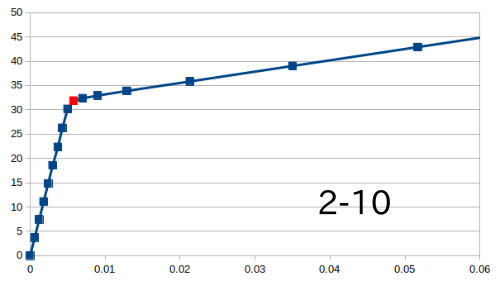
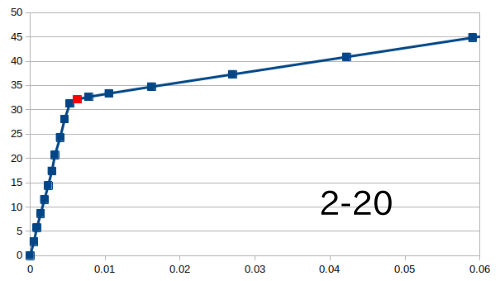
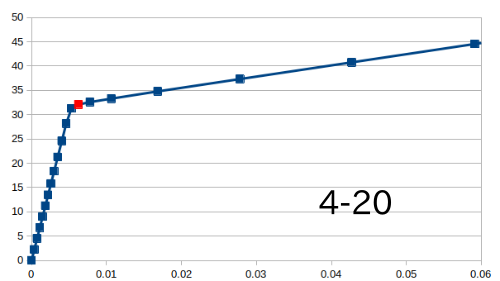
2✕6材の解析結果†

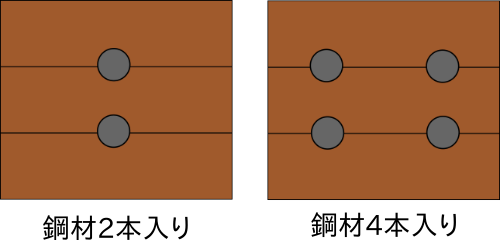
• 丸鋼の直径と本数を変えて解析を行った
• モデルは断面114mm✕140mmで長さ2mの部材において、丸鋼の本数を2本と4本でそれぞれ直径12mmと18mmのモデルを作成
• 

ねじれ座屈解析†

• モデル：10mm(幅)×20mm(厚さ)×1000mm,E=7GPa,ν=0.4
• STAT_NON_LINEで表現できないか試してみる
• 

  荷重を上げていくと変形方向が段階的に変わるような挙動が得られた。ねじれ座屈とはとはいえないので別の設定方法を考える。

• CALC_MODEで再挑戦
• 

  9/1近藤さんにねじれ座屈の設定についてアドバイスをいただき、荷重をかける向きを軸方向から厚さ方向に変えて設定したところねじれ座屈のような挙動が得られた。
  座屈荷重97.849N（1次モード）
  
  ・理論値との比較をしようと「Trahairの座屈公式」から理論値を算出しようとしたが、式に使用されている定数が分からず調べることに...
  ・J=棒部材のねじり定数→GJ=ねじり剛性、Iω=そりねじり定数→EIω=そりねじり剛性であって、ねじりには純ねじりとそりねじりがある。
  ・矩形断面における各定数はどう決定されるのか？→後藤さんからねじり定数とそりねじり定数を計算可能なプログラムを教えてもらったので、それを使用して計算。

• Trahairの座屈公式 \( P_{cr}=\frac{\sqrt{EI_yGJ}}{l^2}(3.95+3.52\sqrt{\frac{\pi^2EI_ω}{GJl^2}}) \)

  9/28~芯材（鋼材）を入れたモデルと穴が空いたモデルの横ねじれ座屈解析をおこなう
  1.断面80mm×50mm、長さ1000mmの木材に断面15mm×15mmの鋼材が入ったモデル
  2.上の木材のみのモデルの側面に、断面60mm×30mmの穴を開けて穴の位置を変えながら解析

1. 行った解析は比較のために鋼材を入れたモデルの他に木材のみと、鋼材が入る部分が穴あきのモデルの3種類 結果としては、木材のみ21.931kN,穴あき21.931kN,鋼材入り25.261kN
2. 穴の開け方は線形座屈のときと同様で結果はグラフのようになった。

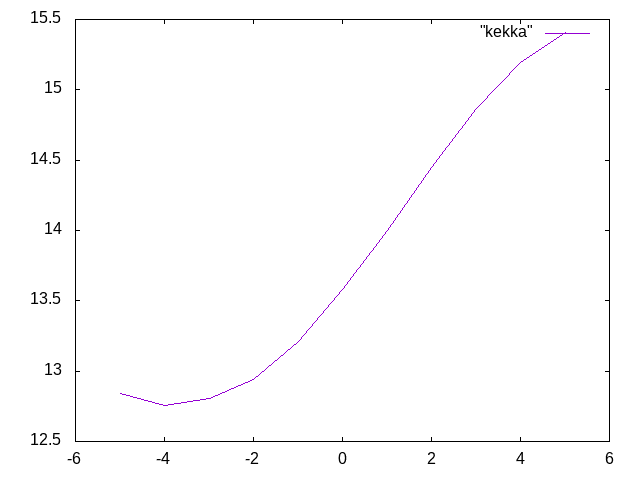
座屈解析†

• https://hitoricae.com/2021/01/31/%e8%96%84%e6%9d%bf%e7%ad%92%e3%81%ae%e7%b7%9a%e5%bd%a2%e5%ba%a7%e5%b1%88%e8%a7%a3%e6%9e%90/
• https://www.code-aster.org/V2/doc/default/en/index.php?man=commande

  ・上のページを参考にしてAsterStudyの設定をしてみた。マトリクス関連の設定でエラーが出た。「MATR_RIGI」、「MATR_RIGI_GEOM」
  ・上のエラーは線形解析を行うことで解消される
  ・5/31時点でAsterStudyの設定で赤くエラーが表示されることはなくなった。
  （この時のコマンドファイル）http://www.str.ce.akita-u.ac.jp/~gotouhan/j2020/tamura/buckling_TR.comm
  ・上のコマンドファイルでは「no eigen mode in the waveband requested.」のようなエラーがでた。固有値が設定されてないっぽい
  ・6/2時点で計算可能になった。
  （この時のコマンドファイル）http://www.str.ce.akita-u.ac.jp/~gotouhan/j2020/tamura/buckling_TR1.comm
  改善した理由としてはCALC_MODESのCALC_CHAR_CRITの値を変更したからだと思われる。→CALC_CHAR_CRITに入れる値は固有値とモードの捜索範囲を指定するものらしい。
  ・座屈した時の梁の挙動は解析結果に示したようであるが座屈荷重のアウトプットが目に見えてはっきりしているものでないため検討する必要がある。

  ✧座屈解析などの固有値解析で求められる固有値\( \lambda \)（ParaVisの"Time"の値）は、与えた条件に対する倍率なので、\( P_{cr}=\lambda \times P \)が座屈荷重になります。特に理由がないのであれば、与える条件を単位荷重（P=1kNとか）にしておくと"Time"の値がそのまま座屈荷重になるので楽なんじゃないかと（6/2近藤）。

・6/7~は座屈解析ができるようになったので、これを利用した応用的な解析をしていく。まず正方形断面でも解析できることが確認できたので予てから行っているモデルで座屈解析を行っていこうと思う。
・木材90mm×90mm×1200mmのモデルで断面の中心に16mm×16mmの鋼材が入ってるモデルの解析を行った結果、2000kN以上の座屈荷重が出てきた。これの示すことは鋼材まで座屈する時の荷重であると考えられる。鋼材が入った際に木材のみが座屈する状態を作る設定を考える必要がある。
・確認のため鋼棒のみ、木材のみ、穴の空いた木材のモデルで座屈解析して、解析値と理論値の座屈荷重を比べてみた。
・90×90×1200の鋼材を座屈解析したところ2000kN以上の座屈荷重が出たので鋼材が入ったモデルの設定を見直してみたら材料設定のミスが見つかった。設定を直して解析を行ったところ72.1194kN(6.94%)の座屈荷重が得られた。

・6/14~ モデルをより実際に近づけるために、木材に異方性を設定して座屈解析を行う。解析を行ったのは断面90×90mmの木材一材料のモデルと、その中に16×16mmの鋼材が入ったモデルである。
・解析を行った結果求められた座屈荷重は、木材のみの方が65.922kN(0.52%)、鋼材の入った方が68.895kN(2.16%)であった。
・

・6/28~ 要素を変えて座屈解析してみる。
 1.梁要素を使って座屈解析する。←青木さんから他のソフトで解析をした結果理論値に近くなったとのことだったのでsalomeでも確かめてみる
   モデル90×90×1200の木材（ヤング率7GPa,ポアソン比0.4）で行った結果、座屈荷重は65.579kN()と求められた
 2.ソリッド要素を使って、鋼材の位置を中心からずらした場合の座屈解析を行う

・7/5~ ねじれ座屈解析
メモ：Trahairの座屈公式
STAT_NON_LINEで表現できないか

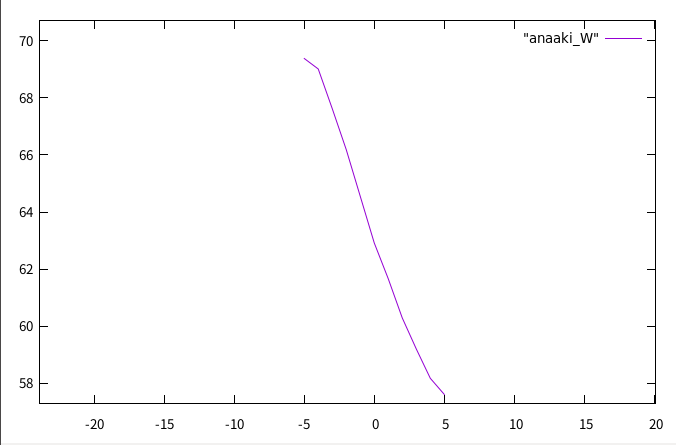
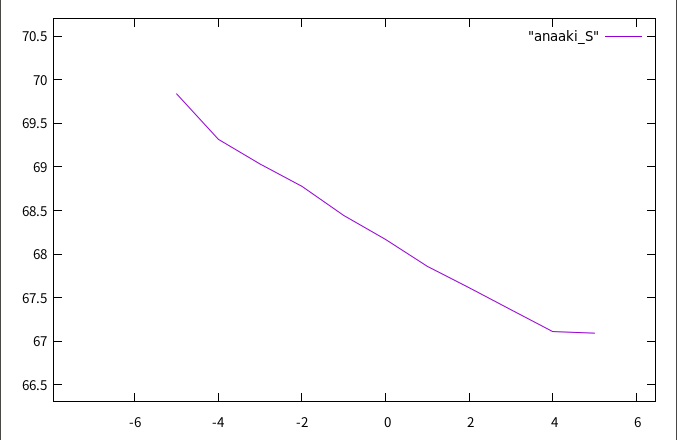
・7/26~ 柱部材に穴が空いている時の座屈解析
モデル：90×90×1200mmの木材（E=7000,ν=0.4）
1.穴の形状を変化させたときの座屈荷重の変位を確かめる
2.穴の位置を変化させたときの座屈荷重の変位を確かめる

1. 
2. 

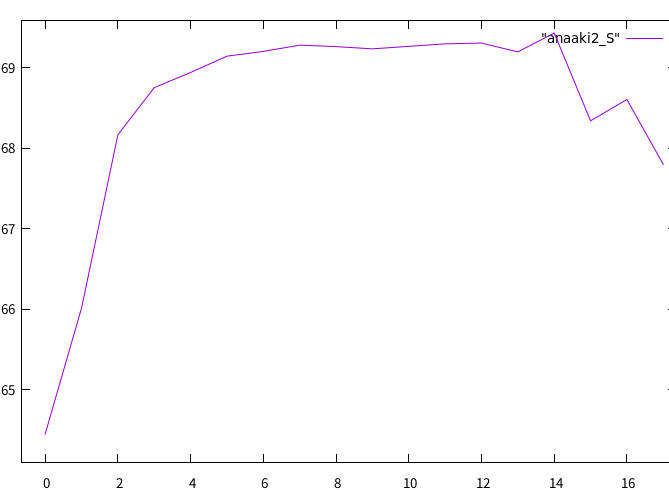
初めての座屈解析の解析結果†

• モデル断面80mm×60mm、高さ1000mm、E=7GPa、ν=0.4、P=300kN

1. 
2. 
3. 
4. 

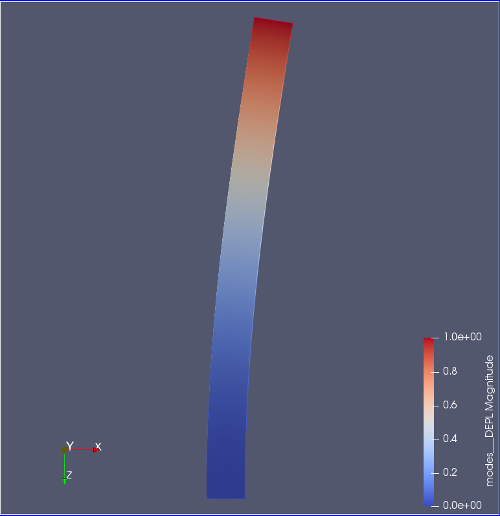
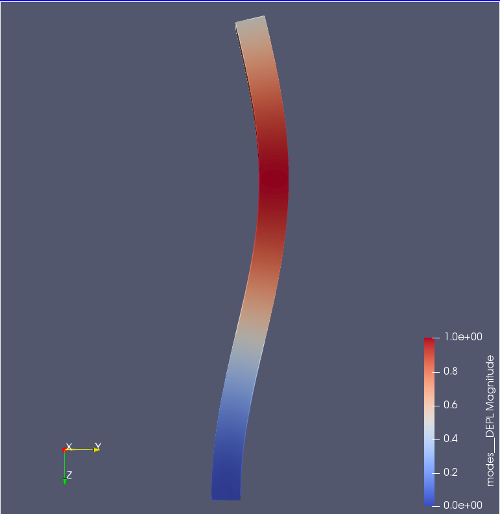
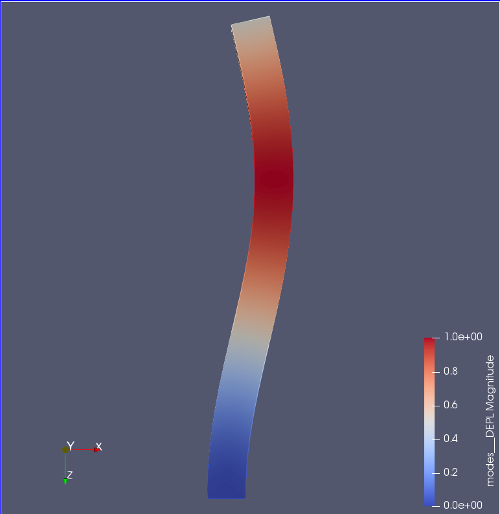
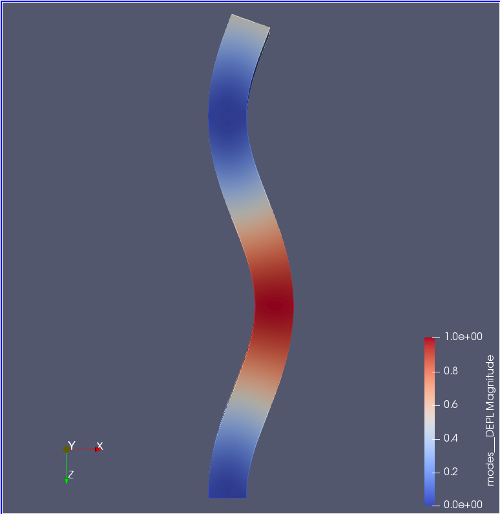
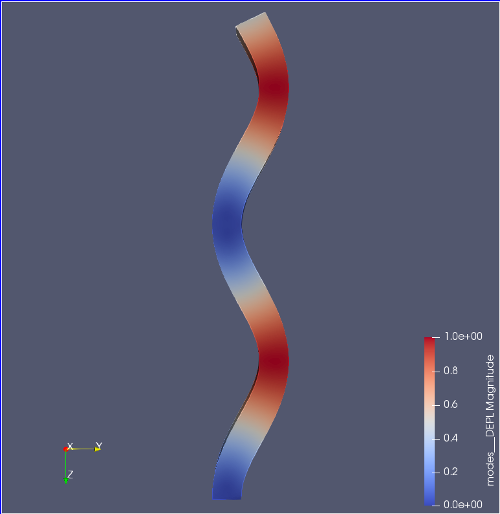
• 各モードの座屈荷重

  座屈荷重[kN]

  	弱軸方向	強軸方向
  1次モード	27.130	46.432
  2次モード	238.27	400.34
  3次モード	630.96	1026.0
  4次モード	1157.0

5/10~†

• もらった実験結果との比較をするためにモデルの作成と解析を行う
• モデルは90mm×90mm×1200mmの柱荷重

1. 真ん中に断面16mm×16mmの正方形の穴が空いた木材

• 200kN荷重時たわみ　解析値:4.350275　理論値:4.370948(-0.473%) 実験値:2.9(50%)

1. 穴に16mm×16mmの鋼材が入った

• 200kN荷重時たわみ　解析値:2.369955　理論値:2.261846(4.78%) 実験値:2.25(5.33%)
• 300kN荷重時たわみ　解析値:3.418366　理論値:3.392770(0.754%) 実験値:3.2(6.82%)
• 

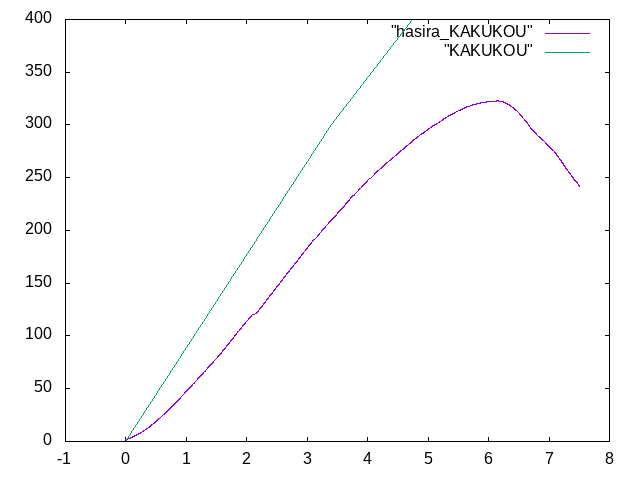
1. 真ん中に半径8mmの鋼棒が入った

• 200kN荷重時たわみ　解析値:2.7934175　理論値:2.5129587(11.16%) 実験値:3.3(-15.35%)
• 300kN荷重時たわみ　解析値:4.1901825　理論値:3.7694380(11.16%) 実験値:5.1(-17.84%)
• 

半径8mmの鋼棒解析†

• たわみ理論値60.228,解析値60.216
• 解析値と理論値の差はほぼなく解析できた
• 理論値は2材料のときのように木材と鋼材の曲げ剛性を足して計算した
  • 円の断面二次モーメント→\( I=\frac{πr^{4}}{4} \)

• 
• 

• salomeでモデルを変えて解析する場合はコマンドファイルを移す方法が便利
• すでに出来てるコマンドファイルをエクスポート
• 新しいモデルでAdd stageする際にインポート→メッシュなどを設定し直す

4種類解析してみて†

• どれも理論値と解析値は近い値になったのでうまく解析はできたと思う。
• たわみの値の大きさの順番は木材→サンドイッチ→鋼材だと思っていたが解析結果ではサンドイッチ→木材→鋼材の順だった。この結果に違和感を感じるが理論値がこの結果が正しいことを裏付けている。
• 青木さんより、得られたたわみの差は大きな差ではないのでどちらがよりたわんだかはさほど気にすることはないとのこと→次のステップへ

4/26~†

• 200×200×3000mmの単純梁に100kN荷重をかけた解析を各材料について行う
• たわみの理論値は以下の式より求める\( v=\frac{P\ell^{3}}{48EI} \)
• 100kN=10.2t→2Lペットボトル5000本分くらい
  • ①E=200GPa,ν=0.3
• 
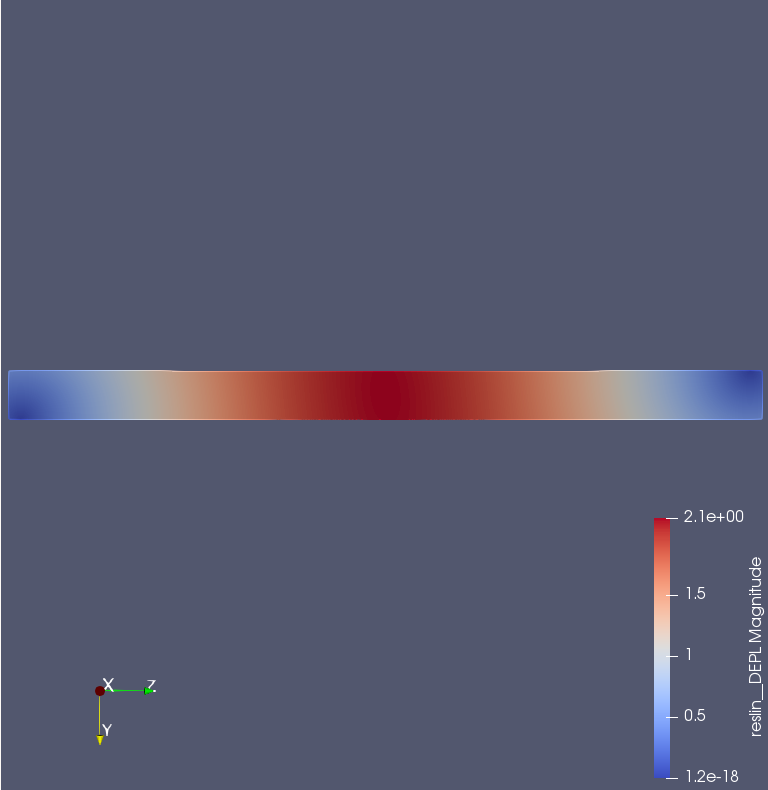
• 理論値:2.109,解析値:2.113
  • ②E=7GPa,ν=0.4
• 
• 理論値:60.268,解析値:60.191
  • ③木材、鋼材をサンドイッチした際の理論値を計算して仮定のヤング率を設定
• 
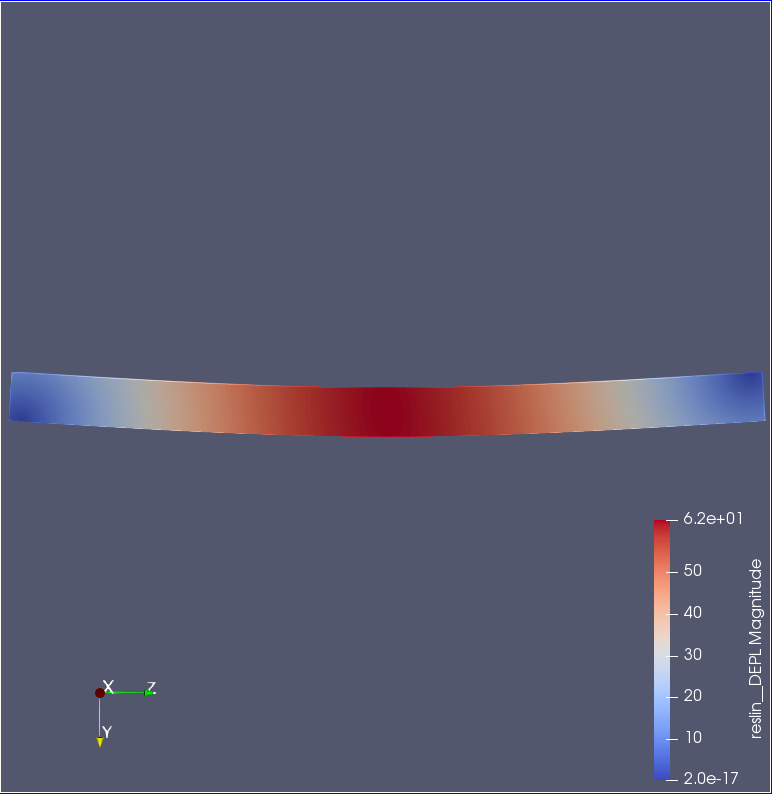
• 理論値:62.114,解析値:62.037
  • ④実際にサンドイッチしたモデルを作成して解析→2材料を参考
• 
• 理論値:62.111,解析値:60.196

4/19~4/25†

• salomeを使った座屈解析の方法を調べる
• https://www.code-aster.org/V2/doc/default/en/man_u/u4/u4.52.02.pdf
• https://www.code-aster.org/V2/doc/default/en/index.php?man=commande
• ↑のページを読めば分かるかも？
• 座屈は難しいので一旦置いといて簡単なモデルで解析していく

imagemagick†

• http://www.protein.osaka-u.ac.jp/rcsfp/supracryst/suzuki/jpxtal/Katsutani/gif1.php
• https://pen.envr.tsukuba.ac.jp/~torarimon/?Imagemagick

作業日誌†

11/13 Salomeの宿題†

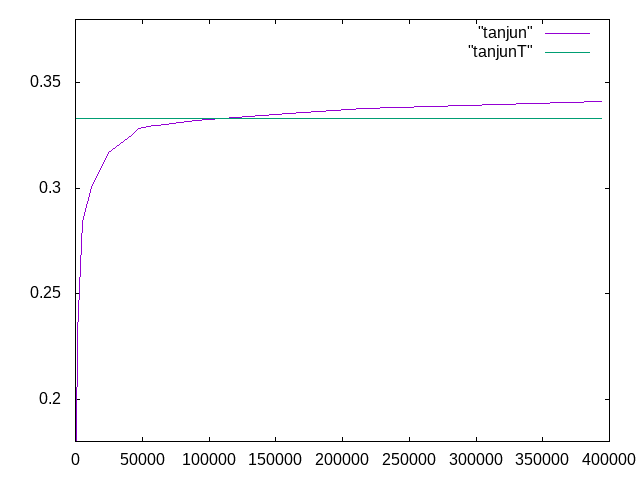
11/20 Salomeの宿題（単純梁）†

ヤング率：7500N/mm＾2　ポアソン比0.4　断面積　10mm×10mm

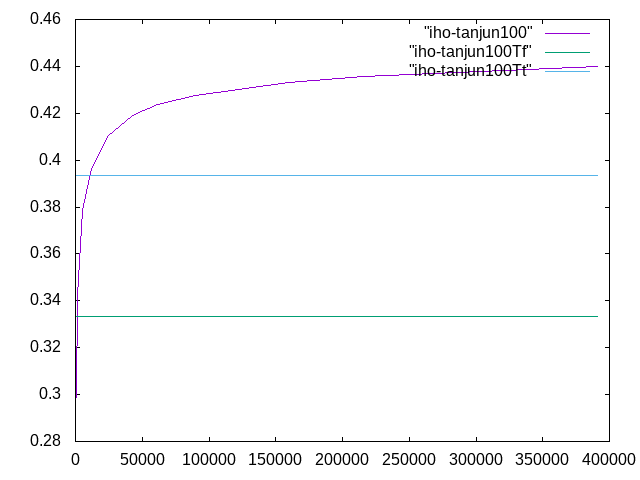
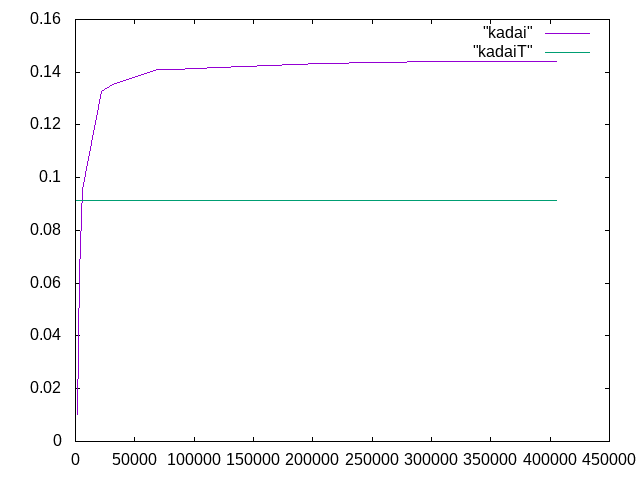
11/20課題「異方単純梁」†

スパン長100mm、

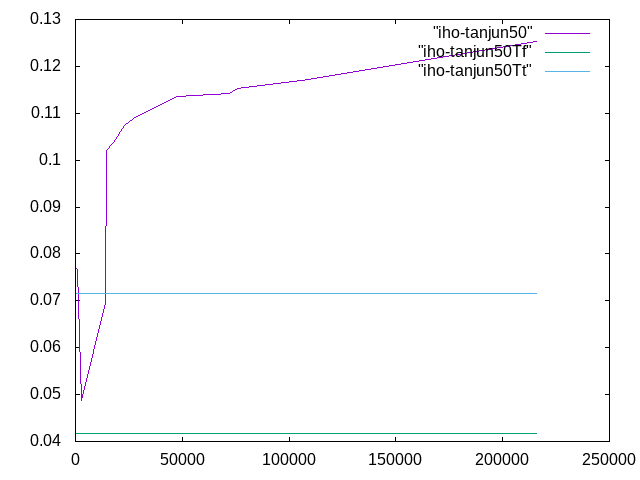
スパン長50mm、

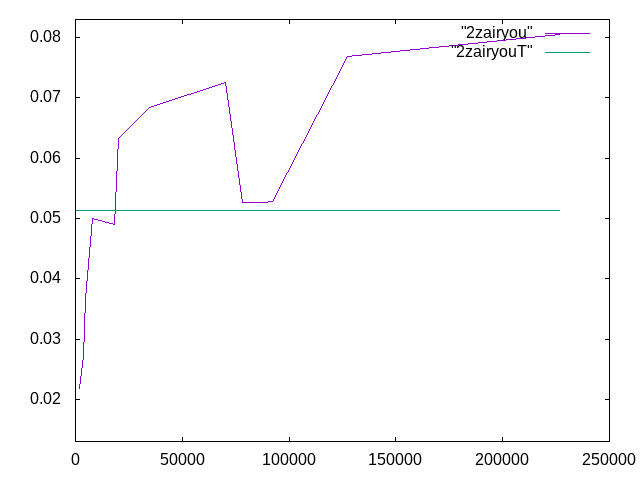
12月4日課題「2材料」†

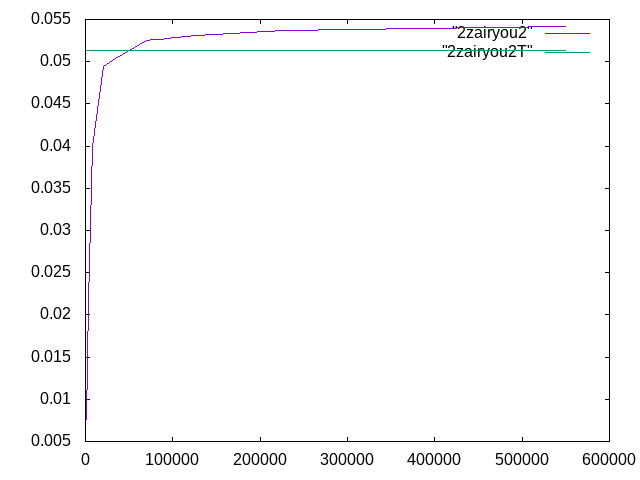
創造工房課題†

10mm×10mm木材断面の縦軸中心に1mm×10mmの鋼材が入った、スパン長100mmの単純梁

最新の100件