![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
タイトル
ケーブル腐食を考慮した3D斜張橋モデルの終局強度に関する検討
概要
斜張橋のような吊形式の橋梁においてケーブルは外力に抵抗する重要な部材である.
近年それらの橋梁のケーブル腐食が問題となっており,実際にケーブル腐食が原因で崩落事故も発生している.
このことを踏まえ,弾塑性解析から健全時とケーブル腐食時の終局強度を算出し,~腐食が橋全体に与える影響を検討した.
ケーブル部を梁要素、桁をシェル要素でつくる
主径間長300mの斜張橋モデルを作成していく。簡易モデルと同様にケーブルを梁要素、桁をシェル要素でつくる。
・5月27日 橋桁、タワー完成
スイープと再番号付けまでは完了した。今後、ケーブルを作成しモデルを完成させる。
・5月30,31日 モデルの完成
来週のゼミまでには形状・材料特性を設定し、梁ピン結合を行う。
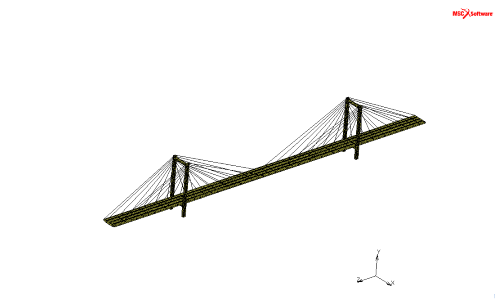
・6月3日 梁ピン結合
ケーブルをタワーと桁にピン結合した。来週はこの続きとバネ結合、境界条件の設定をする。
また、次回ゼミまでには最低一回は解析を行いたい。
・6月7日 梁ピン結合完了
・6月9日 境界条件、バネ結合の設定完了
チェックはできたが、回らないので試行錯誤中
・6月10日 検討1
境界条件や材料特性に問題はなさそう。
角田さんが桁のみで解析を行ったときは解析ができたが、変位図を見てみると一体化されてないかもとのこと。
サーフェス設定時の向きも考えながら、桁のみで一度モデルを作ってみる。
・6月13日 検討2
桁からモデルを作り直した。桁の一端を固定端に、もう一端を自由にして載荷。
model 300と同様の荷重をかけた結果、一体化の問題はなさそう。
Marcにおけるシェル要素の一体化の問題は、サーフェス設定時のポイントの選択の順を統一することで解決できた。
・6月14日 検討3
桁のモデルにタワーも作成して解析したがエラー。
エラーメッセージはmodel 300の解析時と同じ(終了番号2004)だった。
・6月15日
タワーを梁要素として設定、解析を行った。
しかし、同様のエラー(終了番号2004)。
・6月22日
タワーだけのモデルにして点荷重を与えて解析してみた。
結果は今までと同じエラー(終了番号2004)。
・6月27日
タワー(梁要素)と桁(シェル要素)のモデルの解析に成功した。
また、同時進行で作成していたタワーのみ(シェル要素)のモデルも解析に成功した。
シェルで行けそうか確認して引き続きモデル作成していく。
・6月28日
新しいmodel300(タワー、桁→シェル要素)が完成した。以下model300_1
・7月1日
model300(タワー→梁要素、桁→シェル要素)の作成。以下model300_2
model300_2の作成と同時進行でmodel300_1の断面照査を行い、model300_2が完成次第、2つのモデルを比較していく。
・7月14日
スパン中央の変位が10m。明らかに大きすぎる。中央と塔の部分に橋軸方向と垂直方向の仕切りを入れてみる。
・7月20日
変位が10mから約2m程度に小さくなった。
まだ角田さんの解析結果と比較しても大きいのでケーブル位置に同様の仕切りを入れてみる。
・7月22日
主径間には入れ終わった。ただ部分的に変位が大きくなっており、
最大の変位がスパン中央部になっていない。もう少し検討する。
・7月29日
桁の10mごとに仕切りを入れることにした。その結果、部分的に大きくなっていた変位がなくなり、
2Dモデルの変位と比較しても違和感のない結果になった。
・8月19日
ケーブル部の節点が分離している。スイープの方法が適切でなかった。
そのため、スイープ時に節点番号を打ち込む方法で無事に結合できた。モデル完成。
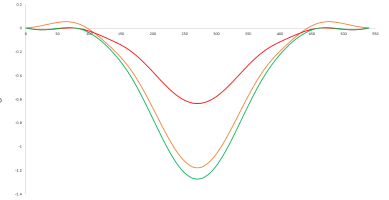 緑:D+CW、赤:D+CW+Pr、黄:D+CW+Pr+L
緑:D+CW、赤:D+CW+Pr、黄:D+CW+Pr+L
・10月5日
要素による変位の影響
元のモデル(四辺形(4),1次要素)
変位:-1.18244mm
2次要素
変位:-1.18553mm
四辺形(8)
要素タイプ75
変位:-1.17581mm
要素タイプ22
変位:-1.17581mm
要素クラスによる変位の変化はあったものの、許容できる範囲であると判断し弾塑性解析に進む.
・10月18日
バネの本数を6本から14本に増やした.
また、シェル要素の表と裏を揃えた.これがどこにどの程度影響しているかは分からないが、
シェル要素のモデルでは確認する必要がありそう.
→弾塑性解析の解析ステップが少し伸びた.線形解析では違いが見られなかったが,弾塑性解析に影響してくるかも.
・8月22日
弾塑性解析開始。回りはするが、解析時間マックスまで解析してくれない。
・9月13日
簡易モデルでは弾塑性解析成功。model300のケーブル無しでも成功した。
・9月16日
model300のケーブルを減らして解析してみた。
スパン中央のケーブル8本(C13,14)だけなら最後まで解析してくれるが段階的に荷重がかからない..
簡易モデルの弾塑性解析も、少し挙動がおかしいかも...
要素タイプを75にして解析してみる.
・9月28日
model300の弾塑性解析成功.もう少しステップ数を増やして解析する.
また,クラス変更から2次要素や四辺形(8)へ変更できることが分かった.
一度弾塑性解析をストップして要素のモデルへ与える影響を検討する。
・10月7日
ステップ数を増やした弾塑性解析を試したが回らない。また、要素を4変形(8)に変更したモデルでもまわらなかった。
・10月11日
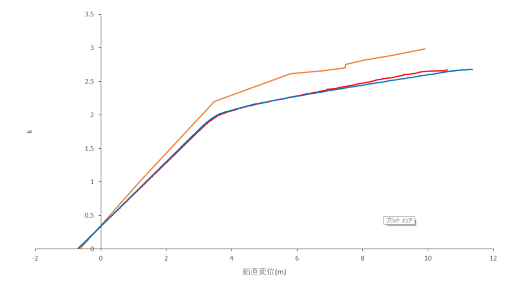
角田さんの2Dモデル、中村先生のモデルとの比較.
黄色:3D、青色:2D、赤色:中村先生
・11月16日
要素数が多いから収束してくれない?→塔を梁要素に変更することを視野に入れて、桁とケーブルだけで弾塑性解析してみる。
ケーブルと桁だけでも段階的に載荷してくれない。→ケーブルの断面積を大きくしてみる。
→段階的に載荷された。塔を梁要素に変更する前にケーブルの断面積を大きくして解析してみる。
・11月18日
ケーブルの断面積による改善は見られなかった
塔をはり要素に変更して解析。→ステップ数は増えた。結果を細かく見ていく
・11月25日
降伏の順番がケーブル→塔の順番。桁に関しては降伏応力に達していない。
色々と試したが結果に変化がないため梁ピン結合に問題があると考え、ケーブルをトラス要素に変更して解析する。
・12月5日
ケーブルをトラス要素に変更。しかし結果は変わらなかった。
・12月15日
要素が重なっている節点(上縁フランジとウェブ、下縁フランジとウェブといった)では応力が正しく出力されない。
よって荷重をかける節点(補剛材)の間隔を10mで固定し、全要素を1m×1mの要素へ細かくする。
・久々の更新
ケーブル健全時の崩壊過程をまとめていた.
また,ケ-ブル腐食を断面積の減少で再現し,両側ケーブル腐食・片側ケーブル腐食の解析を行った.
両側ケーブル腐食では断面積の減少率と崩壊荷重係数が線形的に推移した.
片側ケーブル腐食では橋梁形状のねじれが生じ,腐食ケーブル側のウェブが先行して降伏した.
| 日時 | 作業時間 | 作業内容 |
| 10/15 | 90分 | 顔合わせ |
| 10/21 | 30分 | タッチタイプ |
| 10/22 | 90分 | コマンド練習、タッチタイプ |
| 10/29 | 90分 | gnuplot練習 |
| 11/5 | 90分 | salome片持梁の解析 |
| 11/9 | 80分 | 片持梁の課題 |
| 11/12 | 90分 | salome単純梁の解析 |
| 11/17 | 60分 | 単純梁の課題 |
| 11/19 | 90分 | salome単純梁(異方)の解析 |
| 11/25 | 60分 | 単純梁(異方)の課題 |
11/5
片持梁の解析結果
片持梁の先端変位(集中荷重)の理論値
Pl^3/3EI
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差 | 計算者 |
| 0.5 | 333932 | 6.564 | -1.54 | 新谷 |
| 0.7 | 218976 | 6.541 | -1.89 | 安部 |
| 0.9 | 71718 | 6.431 | -3.54 | 梅宮 |
| 1.2 | 33635 | 6.304 | -5.45 | 七五三 |
| 1.4 | 7699 | 6.316 | -5.26 | 柴田 |
| 1.5 | 4444 | 6.121 | -8.19 | 小池 |
| 1.8 | 2293 | 5.737 | -14.0 | 岩崎 |
| 2 | 2296 | 5.738 | -13.9 | 畠山 |
| 3 | 3487 | 5.474 | -17.9 | 新谷 |
| 4 | 1255 | 3.616 | -45.8 | 安部 |
| 5 | 516 | 4.824 | -27.6 | 岩崎 |
| 6 | 520 | 4.818 | -27.7 | 小池 |
| 7 | 339 | 1.412 | -78.8 | 七五三 |
| 8 | 183 | 4.041 | -39.4 | 柴田 |
| 9 | 191 | 4.002 | -40.0 | 畠山 |
| 10 | 596 | 3.463 | -48.1 | 梅宮 |
11/12
単純梁の解析結果
単純梁の変位の理論値
Pl^3/48EI
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 662117 | 0.429 | 2.89 | 新谷 |
| 0.7 | 145352 | 0.424 | 1.7 | 安部 |
| 0.9 | 105952 | 0.4235 | 1.68 | 梅宮 |
| 1 | 89494 | 0.420 | 0.719 | |
| 1.2 | 32647 | 0.405 | -2.83 | 七五三 |
| 1.4 | 36747 | 0.406 | -2.53 | 柴田 |
| 1.5 | 15675 | 0.396 | -5.04 | 小池 |
| 1.8 | 11493 | 0.394 | -5.5 | 岩崎 |
| 2 | 10495 | 0.395 | -5.09 | 畠山 |
| 3 | 2356 | 0.321 | -23.0 | 新谷 |
| 4 | 1470 | 0.330 | -20.9 | 安部 |
| 5 | 429 | 0.143 | -65.7 | 岩崎 |
| 6 | 355 | 0.125 | -70.0 | 小池 |
| 7 | 415 | 0.0997 | -76.1 | 七五三 |
| 8 | 109 | 0.124 | -70.3 | 柴田 |
| 9 | 91 | 0.135 | -67.7 | 畠山 |
| 10 | 237 | 0.0776 | -81.4 | 梅宮 |
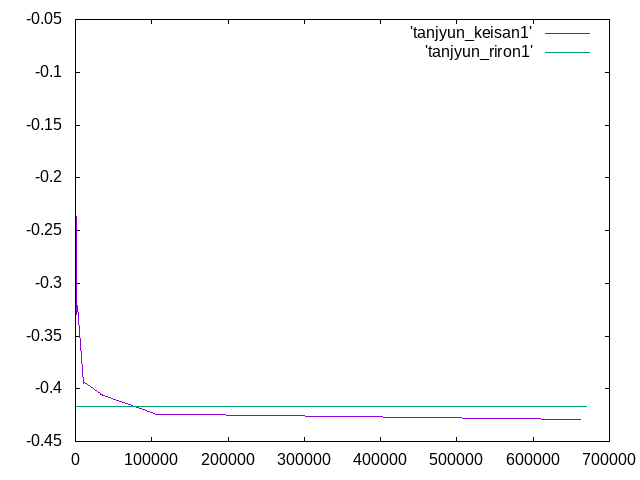
今回、荷重の逆向きをy軸正としたので変位は負となり、グラフは下図のようになった
11/19
単純梁(異方)の解析結果
ティモシェンコ梁理論による変位の理論値
(PL^3/48EI)+(PL/4kGA)
・1次
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 939345 | 0.552 | 12.2 | 新谷 |
| 0.7 | 169112 | 0.540 | 9.76 | 安部 |
| 0.9 | 105952 | 0.537 | 9.15 | 梅宮 |
| 1.2 | 32647 | 0.518 | 5.29 | 七五三 |
| 1.4 | 17737 | 0.514 | 4.47 | 柴田 |
| 1.5 | 15675 | 0.511 | 3.86 | 小池 |
| 1.8 | 11710 | 0.507 | 3.05 | 岩崎 |
| 2 | 10495 | 0.506 | 2.79 | 畠山 |
| 3 | 3885 | 0.451 | -8.33 | 新谷 |
| 4 | 2311 | 0.447 | -9.14 | 安部 |
| 5 | 431 | 0.290 | -41.1 | 岩崎 |
| 6 | 347 | 0.341 | -30.7 | 小池 |
| 7 | 415 | 0.220 | -55.3 | 七五三 |
| 8 | 109 | 0.243 | -50.6 | 柴田 |
| 9 | 91 | 0.251 | -48.9 | 畠山 |
| 10 | 237 | 0.211 | -57.1 | 梅宮 |
・2次
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 939345 | 0.563 | 14.4 | 新谷 |
| 0.7 | 169112 | 0.567 | 15.2 | 安部 |
| 0.9 | 105952 | 0.565 | 14.8 | 梅宮 |
| 1.2 | 32647 | 0.555 | 12.8 | 七五三 |
| 1.4 | 17737 | 0.554 | 12.6 | 柴田 |
| 1.5 | 15675 | 0.552 | 12.2 | 小池 |
| 1.8 | 11710 | 0.551 | 12.0 | 岩崎 |
| 2 | 10495 | 0.549 | 11.6 | 畠山 |
| 3 | 3885 | 0.540 | 9.76 | 新谷 |
| 4 | 2311 | 0.535 | 8.74 | 安部 |
| 5 | 431 | 0.525 | 6.71 | 岩崎 |
| 6 | 347 | 0.527 | 7.11 | 小池 |
| 7 | 415 | 0.508 | 3.25 | 七五三 |
| 8 | 109 | 0.508 | 3.25 | 柴田 |
| 9 | 91 | 0.508 | 3.25 | 畠山 |
| 10 | 237 | 0.507 | 3.05 | 梅宮 |
11/26
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 652354 | 0.089 | -10.2 | 新谷 |
| 0.7 | 192792 | 0.09193 | -7.3 | 安部 |
| 0.9 | 104548 | 0.0919 | -7.26 | 梅宮 |
| 1.2 | 45045 | 0.09192 | -7.27 | 七五三 |
| 1.4 | 24237 | 0.0919 | -7.27 | 柴田 |
| 1.5 | 19998 | 0.0919 | -7.29 | 小池 |
| 1.8 | 12624 | 0.092 | -7.07 | 岩崎 |
| 2.0 | 10716 | 0.0919 | -7.29 | 畠山 |
| 3.0 | 6000 | 0.092 | -7.07 | 新谷 |
| 4.0 | 2993 | 0.09087 | -8.3 | 安部 |
| 5.0 | 1010 | 0.090 | -9.09 | 岩崎 |
| 6.0 | 836 | 0.0886 | -10.62 | 小池 |
| 7.0 | 1167 | 0.0865 | -12.741 | 七五三 |
| 8.0 | 284 | 0.0847 | -14.53 | 柴田 |
| 9.0 | 261 | 0.0832 | -16.1 | 畠山 |
| 10 | 607 | 0.0874 | -11.8 | 梅宮 |
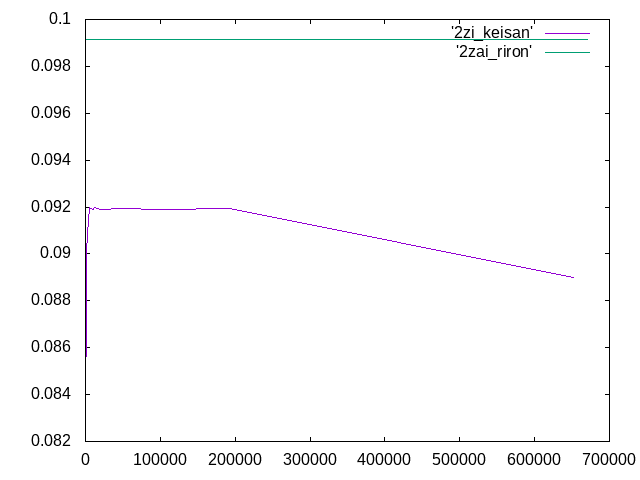
2次で解析を行ったので、要素数が大きくなればなるほど理論値に収束する予想だったが、
グラフが予想に反した形となった。
また、単純梁や張出梁と比較すると変位がかなり小さくなった。