![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
渡辺 ライフスタイルマネジメント 30年後歩きづらくなるのは分かった→何年後手を加えればよいか
荻野 何を基準にどうなったらいけないのか 共振するかしないか 固有振動数をどう制御するのか
平川 固有振動数で歩きやすさは決まるのか?
網田 橋が変わった前後で揺れが変わったのかを感じたかどうか実際に歩いた人にインタビューしたか
局所的腐朽が近代木橋の応答速度に及ぼす影響について 木製歩道橋などでは振動使用性に関する検討が行われている。振動使用性は歩行者が橋を渡る際に生じる振動が歩行者に及ぼす影響(歩きやすいのか、歩きにくいのか)について応答速度の範囲で規定したものである。振動試験をおこない、振動を測定すれば劣化による応答速度の変化なども確認できる。しかしその変化は橋のどの部分が劣化したことによる影響かはわからない。そこでSalome-Mecaの動的応答解析で局所的腐朽の箇所を反映したモデルの解析を行い、橋のどの部分が劣化すると危険な状態になるのか調べる。
2.0Hzの歩行振動を腐朽させためおと橋に加えた。
腐朽前の応答速度が0.219cm/s
腐朽後の応答速度が0.544cm/sで
約2倍近く振幅が増えた。この数値の妥当性を考察しないといけない
1.8Hzのめおと橋の歩行振動解析の結果 測点1の応答速度は0.18cm/sで実測値との誤差が殆どなかった
新めおと橋の腐朽時の固有値振動解析も行った
前回と今回の2回でめおと橋の振動解析を行った。 今回は2.2Hz前回は2.0Hz
解析値は0.219 実測値は0.216 相対誤差1.39%
2回連続で解析途中でサロメが落ちていたので パソコンの容量を確認してかなり使っていたので次回はパソコンの整理をやりたいです。
最大値が3.5977→3.3664
実効値が0.8757→0.7332
に改善した
s/置換前/置換後/g #追加するコマンド
まずは6.26Hzのときの振動数がだいたい200〜250Hzにおさまっていることが今までの解析でわかった(1人の場合)。
次に2Hzのとき、これは及川さんに解析してもらい80Hzくらいになっている。
つまり約3倍程度しか共振によって振幅が増えていないことがわかった。
しかし、小野測器の参考資料によると減衰定数が0.05以下で共振した場合は振幅が10倍になるということがわかっている。そして実験によって得られた減衰定数は0.018なので、今回の3倍になった解析では正しく再現ができていないことになる。
なので今度は砂袋落下試験によって減衰定数を求めることにした。



 http://www.str.ce.akita-u.ac.jp/~gotouhan/j2021/shintani/
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2021/shintani/
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2021/shintani/
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2021/shintani/
シンメオト橋の固有振動数である6.26Hz、アーチ部材のみの固有振動数2.22Hzの振動を与えて共振をするのか計算した。
6個のグラフは6.26Hzを与えたときの振幅と時間のグラフ
現在は5人で歩かせています。 来週以降は50Hzで5にんで歩かせて比較対象を作りたいです。
前回に引き続き腐朽箇所を作成した。 今回はアーチ面に作成した。
今回から実際に腐朽箇所を作成し、その箇所のヤング率を変更することで模擬的に腐朽を再現する。
吊り床と縦桁の交点部と縦桁の継ぎ接ぎ部に上面から厚さ30mm、交わっている場所は余分に50mmで作った。
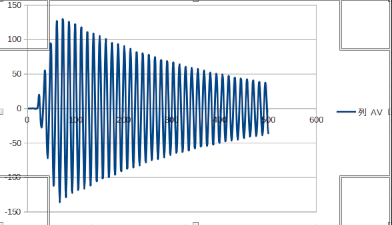
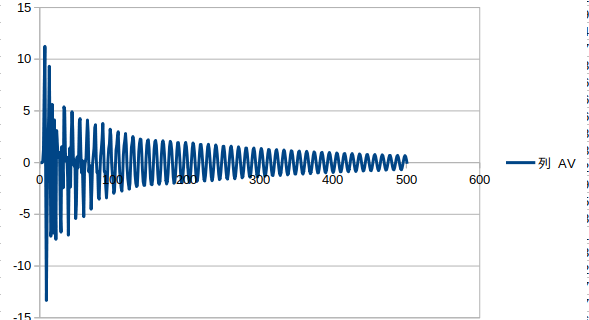
前回は固有振動数が2.0Hzの梁に歩調2Hzをあたえ振動させた。今回は固有振動数を同じ値をとって歩調(3.5Hz)をかえて振動させた。その結果観測点の速度が小さくなり前回の速度が共振によって大きくなっていることが比較してわかった。つまり前回の梁は共振しているということになる。
歩調2Hzのときのグラフ
 縦軸が速度(mm/s)
横軸が数値の番号(0秒から20秒)
縦軸が速度(mm/s)
横軸が数値の番号(0秒から20秒)
歩調3.5Hzのときのグラフ
 縦軸が速度(mm/s)
横軸が数値の番号(0秒から25秒)
縦軸が速度(mm/s)
横軸が数値の番号(0秒から25秒)
振幅倍率 https://www.onosokki.co.jp/HP-WK/c_support/newreport/dampingfactor/dampingfactor_2.htm
歩調が2Hzの場合のモデルを作成した。 理論式より固有振動数を2になるようにλ=π、ρ=3.8×10^-10、E=7000Pa、幅1000mm、厚さ100mmとして長さを求めた。 以上の値を代入し長さ9864mmを求めた。
長さ:幅:厚さ=9864:1000:100(mm)の直方体を作成した。
減衰定数を0.001に設定したが大きすぎて減衰の様子を確認することができなかった。次回は時間を長くして減衰が起こっているかを確認する。 また共振していることを確認するためには歩調を2Hzからさらに高い振動数にする。
歩行者の歩行による振動が主桁の振動と共振することで歩行者に不快感を与えててしまう問題が起きている。
まず人間の歩行は約1秒で2歩進む。この歩調と橋の固有振動数が一致すると共振が発生する。 この共振を起こさないためには橋の固有振動数を一次振動、二次振動において固有振動数を1.5〜2.3Hzを避けるのが好ましい。
この他にも風などによる外力による動的安定性をもたせなければならない
桁形式歩道橋の設計時振動使用性照査手法の提案 田中信治 加藤雅史
振動感覚を考慮した歩道橋の使用性照査法に関する考察 梶川康男
橋梁振動の人間工学的評価法 小堀為雄 梶川康男
振幅倍率 小野測器のサイト https://www.onosokki.co.jp/HP-WK/c_support/newreport/dampingfactor/dampingfactor_2.htm
| 日時 | 内容 |
| 2021.10.15 | 顔合わせ |
| 2021.10.22 | 研究室入室 |
| 2021.10.27 | gnuplotの操作 |
| 2021.11.5 | 片持ち梁のsalome計算(欠席) |
| 2021.11.12 | 単純梁のsalome計算 |
| 2021.11.19 | 直方異方性の単純梁のsaslome計算 |
| 2021.11.26 | 2部材の単純梁のsalome計算 |
| 2021.12.3 | LaTeXとXHTML |
| 2021.12.10 | 現場見学会 |
| メッシュの長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 333932 | 6.564 | -1.5 | 新谷 |
| 0.7 | 218976 | 6.541 | -1.9 | 安部 |
| 0.9 | 71718 | 6.431 | -3.5 | 梅宮 |
| 1.2 | 33635 | 6.304 | -5.4 | 七五三 |
| 1.4 | 7699 | 6.316 | -5.3 | 柴田 |
| 1.5 | 4444 | 6.121 | -8.2 | 小池 |
| 1.8 | 2293 | 5.737 | -14.0 | 岩崎 |
| 2 | 2293 | 5.737 | -13.9 | 畠山 |
| 3 | 3487 | 5.474 | -17.9 | 新谷 |
| 4 | 1255 | 3.616 | -45.8 | 安部 |
| 5 | 519 | 4.824 | -27.7 | 岩崎 |
| 6 | 520 | 4.818 | -27.7 | 小池 |
| 7 | 339 | 1.412 | -78.8 | 七五三 |
| 8 | 183 | 4.041 | -39.4 | 柴田 |
| 9 | 191 | 4.002 | -40.0 | 畠山 |
| 10 | 596 | 3.463 | -48.1 | 梅宮 |
| メッシュの長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 662117 | 0.429 | 2.89 | 新谷 |
| 0.7 | 145352 | 0.424 | 1.7 | 安部 |
| 0.9 | 105952 | 0.4235 | 1.68 | 梅宮 |
| 1.2 | 32647 | 0.4052 | -2.83 | 七五三 |
| 1.4 | 36747 | 0.40613 | -2.53 | 柴田 |
| 1.5 | 15675 | 0.396 | -5.04 | 小池 |
| 1.8 | 11493 | 0.394 | -5.5 | 岩崎 |
| 2 | 10495 | 0.395 | -5.09 | 畠山 |
| 3 | 2356 | 0.321 | -23.02 | 新谷 |
| 4 | 1470 | 0.330 | -20.9 | 安部 |
| 5 | 429 | 0.143 | -65.7 | 岩崎 |
| 6 | 355 | 0.125 | -70.02 | 小池 |
| 7 | 415 | 0.0997 | -76.091 | 七五三 |
| 8 | 109 | 0.124 | -70.25 | 柴田 |
| 9 | 91 | 0.135 | -67.7 | 畠山 |
| 10 | 237 | 0.0776 | -81.4 | 梅宮 |
一次
| メッシュの長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 939345 | 0.552 | 12.20 | 新谷 |
| 0.7 | 169122 | 0.540 | 9.8 | 安部 |
| 0.9 | 105952 | 0.537 | 9.15 | 梅宮 |
| 1.2 | 32647 | 0.518 | 5.28 | 七五三 |
| 1.4 | 17737 | 0.514 | 4.47 | 柴田 |
| 1.5 | 15675 | 0.511 | 3.86 | 小池 |
| 1.8 | 11710 | 0.507 | 3.05 | 岩崎 |
| 2 | 10495 | 0.506 | 2.79 | 畠山 |
| 3 | 3885 | 0.452 | -8.33 | 新谷 |
| 4 | 2311 | 0.447 | -9.14 | 安部 |
| 5 | 431 | 0.290 | -41.06 | 岩崎 |
| 6 | 347 | 0.341 | -30.69 | 小池 |
| 7 | 415 | 0.220 | -55.29 | 七五三 |
| 8 | 109 | 0.243 | -50.61 | 柴田 |
| 9 | 91 | 0.251 | -48.90 | 畠山 |
| 10 | 237 | 0.211 | -57.1 | 梅宮 |
二次
| メッシュの長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 939345 | 0.563 | 14.43 | 新谷 |
| 0.7 | 169122 | 0.567 | 15.24 | 安部 |
| 0.9 | 105952 | 0.565 | 14.8 | 梅宮 |
| 1.2 | 32647 | 0.555 | 12.81 | 七五三 |
| 1.4 | 17737 | 0.554 | 12.60 | 柴田 |
| 1.5 | 15675 | 0.552 | 12.20 | 小池 |
| 1.8 | 11710 | 0.551 | 11.99 | 岩崎 |
| 2 | 10495 | 0.550 | 11.63 | 畠山 |
| 3 | 3885 | 0.540 | 9.76 | 新谷 |
| 4 | 2311 | 0.535 | 8.74 | 安部 |
| 5 | 431 | 0.525 | 6.71 | 岩崎 |
| 6 | 347 | 0.527 | 7.11 | 小池 |
| 7 | 415 | 0.508 | 3.25 | 七五三 |
| 8 | 109 | 0.508 | 3.25 | 柴田 |
| 9 | 91 | 0.508 | 3.29 | 畠山 |
| 10 | 237 | 0.507 | 3.05 | 梅宮 |
| メッシュの長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 652354 | 0.089 | -10.22 | 新谷 |
| 0.7 | 192792 | 0.092 | -7.30 | 安部 |
| 0.9 | 104548 | 0.092 | -7.26 | 梅宮 |
| 1.2 | 45045 | 0.092 | -7.27 | 七五三 |
| 1.4 | 24237 | 0.092 | -7.27 | 柴田 |
| 1.5 | 19998 | 0.092 | -7.29 | 小池 |
| 1.8 | 12624 | 0.092 | -7.07 | 岩崎 |
| 2 | 10716 | 0.092 | -7.29 | 畠山 |
| 3 | 6000 | 0.092 | -7.07 | 新谷 |
| 4 | 2793 | 0.091 | -8.3 | 安部 |
| 5 | 1010 | 0.090 | -9.09 | 岩崎 |
| 6 | 836 | 0.089 | -10.62 | 小池 |
| 7 | 1167 | 0.087 | -12.74 | 七五三 |
| 8 | 284 | 0.085 | -14.53 | 柴田 |
| 9 | 261 | 0.083 | -16.07 | 畠山 |
| 10 | 607 | 0.087 | -11.8 | 梅宮 |
※メッシュサイズ0.5mmは要素数が大きすぎて1次要素で計算した。