注意：
このページの数式は、
MathJaxを使って書いてます。
数式部分がおかしい場合は、更新ボタンをクリックすると
改善するかも知れません。
太文字のギリシャ文字($\mathbf{\sigma}$など)が、
太文字になっていない($\sigma$)かもしれません。
その他、おかしい記述があると思ったら、
メールなどで指摘して下さい。
構造力学IIで、
「伸び縮み変形」と「せん断変形」とか、それらと対応する直ひずみ、せん断ひずみっていうのは、
座標に依存するから、どの座標で観測するかで変わってくるという話をした。
直応力やせん断応力も同様に座標に依存している。
だとすると、物体内のある点$(x,y,z)$において、そこの応力成分
($x,y,z$座標系で記述するなら
$\sigma_{xx}, \sigma_{yy}, \sigma_{zz}, \sigma_{xy}, \sigma_{yz}, \sigma_{zx}$)が、
別の座標系で記述したら、直応力成分だけで表せる向きみたいなのがあったりするだろうか。
まあ、みなさんは土質とかで、既に主応力という言葉は知っていると思うが、
要は、その主応力というのを導いてみたい。
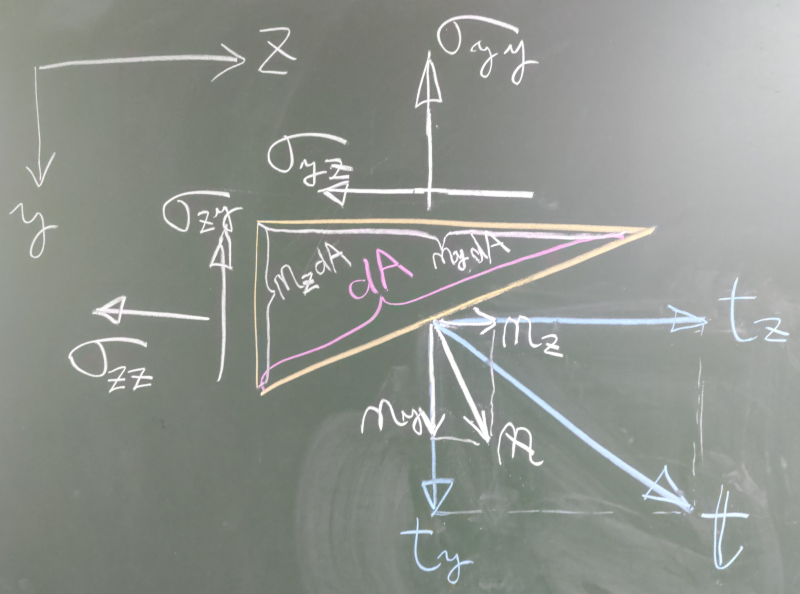応力テンソルの説明によると、
ある任意の断面の微小領域$dA$に作用する表面力ベクトル$\mathbf{t}$は
3次元の場合には以下の応力テンソル$\mathbf{\sigma}$と関係づけることができた。
$t_{x}=n_{x}\sigma_{x x}+n_{y}\sigma_{yx}+n_{z}\sigma_{zx}$
$t_{y}=n_{x}\sigma_{xy}+n_{y}\sigma_{yy}+n_{z}\sigma_{zy}$
$t_{z}=n_{x}\sigma_{xz}+n_{y}\sigma_{yz}+n_{z}\sigma_{zz}$
まとめると
${\displaystyle t_{j}=\sum_{i=x,y,z}n_{i}\sigma_{ij}}
$
(但し$j=x,y,z$)
となる。行列で書くなら、
$
\left(
\begin{array}{c}
t_{x}\\
t_{y}\\
t_{z}
\end{array}
\right)
=
\left[
\begin{array}{ccc}
\sigma_{xx} & \sigma_{yx} & \sigma_{xz} \\
\sigma_{xy} & \sigma_{yy} & \sigma_{zy} \\
\sigma_{xz} & \sigma_{yz} & \sigma_{zz}
\end{array}
\right]
\left(
\begin{array}{c}
n_{x}\\
n_{y}\\
n_{z}
\end{array}
\right)
$
応力の対称条件を考慮すると
$
\left(
\begin{array}{c}
t_{x}\\
t_{y}\\
t_{z}
\end{array}
\right)
=
\left[
\begin{array}{ccc}
\sigma_{xx} & \sigma_{xy} & \sigma_{zx} \\
\sigma_{xy} & \sigma_{yy} & \sigma_{yz} \\
\sigma_{zx} & \sigma_{yz} & \sigma_{zz}
\end{array}
\right]
\left(
\begin{array}{c}
n_{x}\\
n_{y}\\
n_{z}
\end{array}
\right)
$
となる。
これは、物体内のある点$(x,y,z)$を含む断面における
その点$(x,y,z)$の近傍の微小な領域$dA$に作用する表面力ベクトル$\mathbf{t}$を
応力テンソル($\sigma_{xx}$とか$\sigma_{xy}$とか)で表す式だ。
点$(x,y,z)$と$dA$(または、断面からくり抜いた積み木状の微小ピース)との位置関係は
はっきりとは決めてないが、それだとイメージしにくいということであれば、
例えば$dA$の図心とか積み木ピースの図心に点$(x,y,z)$が位置していると考えておいてもいい。
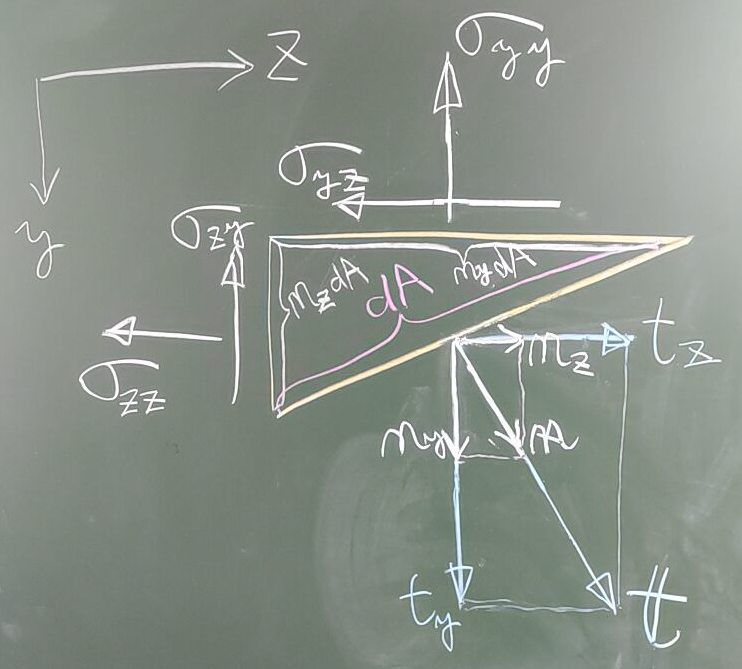今、ある点$(x,y,z)$を含む断面を適当な向きに切ったら、
その点$(x,y,z)$の近傍の微小な領域$dA$
では、図のように、表面力ベクトル$\mathbf{t}$の向きがその断面の法線ベクトル$\mathbf{n}$と完全に一致している
ような場合（つまり、この微小部分の面上にはせん断応力成分が生じておらず、
表面力ベクトルがこの面に垂直な直応力成分だけで表せるような場合）
を考える。
$\mathbf{t}$は、法線ベクトル$\mathbf{n}$のスカラー倍で表せるから、
そのスカラーを$\sigma$と書くことにすると、
$\mathbf{t}=\sigma\, \mathbf{n}$みたいに書ける。
行列を用いて書くなら以下のようになる。
$
\left(
\begin{array}{c}
t_{x}\\
t_{y}\\
t_{z}
\end{array}
\right)
=
\left[
\begin{array}{ccc}
\sigma_{xx} & \sigma_{xy} & \sigma_{zx} \\
\sigma_{xy} & \sigma_{yy} & \sigma_{yz} \\
\sigma_{zx} & \sigma_{yz} & \sigma_{zz}
\end{array}
\right]
\left(
\begin{array}{c}
n_{x}\\
n_{y}\\
n_{z}
\end{array}
\right)
=
\sigma
\left(
\begin{array}{c}
n_{x}\\
n_{y}\\
n_{z}
\end{array}
\right)
$
このような（$\mathbf{t}$の向きが$\mathbf{n}$に一致するような）向きが存在するなら、
上の式で$\mathbf{n}=\mathbf{0}$以外の
(つまり、$n_{x}=n_{y}=n_{z}=0$以外の)$\mathbf{n}$が
存在するということだ。
そのような$\mathbf{n}$が存在する条件は、以下のように表せる。
$
\det\left|
\begin{array}{ccc}
\sigma_{xx}-\sigma & \sigma_{xy} & \sigma_{zx} \\
\sigma_{xy} & \sigma_{yy}-\sigma & \sigma_{yz} \\
\sigma_{zx} & \sigma_{yz} & \sigma_{zz}-\sigma
\end{array}
\right|=0
$
$\det||$は行列式だが、
この式はどこかで見たことがあると思う。
$\sigma$が固有値で、$\mathbf{n}$が固有ベクトルに対応している。
線形代数の教科書の固有値のところを見れば、
同じ表現の式（文字や表記は微妙に違うかもしれないが）がのっている
と思う。
こういうふうに、ゼロでない非自明解を求めたいとき
（例えば、座屈荷重とか固有振動数とか）、固有値を求めるということを
よくやる（で、座屈モードや振動モードが固有ベクトルに対応していると
いったような）。
上の式は、$3\times 3$の行列の行列式だから、スカラー$\sigma$についての
3次方程式になる。
この3次方程式を書き下すのはめんどくさいが、
展開すると、
たぶん次のような感じの式になるのではないかと思う。
$
\sigma^{3}
-(
\sigma_{xx}+\sigma_{yy}+\sigma_{zz}
)\sigma^{2}
+
(
\sigma_{xx}\sigma_{yy}
+\sigma_{yy}\sigma_{zz}
+\sigma_{zz}\sigma_{xx}
-\sigma_{xy}^{2}
-\sigma_{yz}^{2}
-\sigma_{zx}^{2}
)\sigma
\\
-
(
\sigma_{xx}\sigma_{yy}\sigma_{zz}
+2\sigma_{xy}\sigma_{yz}\sigma_{zx}
-\sigma_{xx}\sigma_{yz}^{2}
-\sigma_{yy}\sigma_{zx}^{2}
-\sigma_{zz}\sigma_{xy}^{2}
)=0
$
応力テンソルの各成分（$\sigma_{xx}$とか$\sigma_{xy}$とか）は、
物体内のある点$(x,y,z)$について定義されているものだから、
この3次方程式は、物体内のあらゆる点$(x,y,z)$ごとに3つの解を持つということだ。
この3次方程式の3つの解を大きい順に$\sigma_{1}, \sigma_{2}, \sigma_{3}$と置くと、
それぞれの解（固有値）に対応する固有ベクトル$\mathbf{n}$が
あることになるから、
物体内のあらゆる点$(x,y,z)$ごとに
表面力ベクトルが法線ベクトルと一致する（せん断応力成分が生じない）ような
3面（というか3方向）があるということだ。
これら
$\sigma_{1}, \sigma_{2}, \sigma_{3}$を主応力と呼び、
主応力が作用している面の向き（$\mathbf{n}$の向き）を主方向と呼ぶが、
（3つの主応力のうち、重解にならずに値が異なる主応力どうし）の主方向は直交する。
3つの主応力は、大きい順に
最大主応力($\sigma_{1}$),
中間主応力($\sigma_{2}$),
最小主応力($\sigma_{3}$)と呼ぶが、これらの3つの正負の組み合わせは様々なので、
最大主応力が正で引張で最小主応力が負で圧縮のこともあれば、
3つとも圧縮で負のことも3つとも引張で正のこともある。
有限要素解析ソフト等では、PRN1, PRN2, PRN3みたいに出力されたりするが、
大きい順に並んでいるのか、小さい順に並んでいるのかはソフトによって違うかもしれないので、
PRN1が最大主応力なのか、最小主応力なのか、そういうチェックは重要である。
$\sigma_{1}, \sigma_{2}, \sigma_{3}$を用いると、
上の3次方程式は、解と係数の関係から以下のように書ける。
$\sigma^{3}
-(\sigma_{1}+\sigma_{2}+\sigma_{3})\sigma^{2}
+(\sigma_{1}\sigma_{2}+\sigma_{2}\sigma_{3}+\sigma_{3}\sigma_{1})\sigma
-\sigma_{1}\sigma_{2}\sigma_{3}=0
$
これらの係数を
$I_{1}=\sigma_{1}+\sigma_{2}+\sigma_{3}$
$I_{2}=
\sigma_{1}\sigma_{2}+\sigma_{2}\sigma_{3}+\sigma_{3}\sigma_{1}$
$I_{3}=\sigma_{1}\sigma_{2}\sigma_{3}$
とおくと、3次方程式は、
$\sigma^{3}-I_{1}\sigma^{2}+I_{2}\sigma -I_{3}=0$
のように書け、この$I_{1}, I_{2}, I_{3}$を
それぞれ
応力の第1, 第2, 第3不変量と言う。
式の各項の符号がそろうように
（あるいは、下で出てくる主偏差応力の3次方程式の不変量と符号をそろえて）
$I_{2}$とかが
マイナスをつけたもので定義されている場合もある。
不変量は座標に依存しない量である。
上の3次方程式の係数と比較して、応力テンソルの成分で書けば以下のようになる。
$
I_{1}=
\sigma_{xx}+\sigma_{yy}+\sigma_{zz}
\\
I_{2}=
\sigma_{xx}\sigma_{yy}
+\sigma_{yy}\sigma_{zz}
+\sigma_{zz}\sigma_{xx}
-\sigma_{xy}^{2}
-\sigma_{yz}^{2}
-\sigma_{zx}^{2}
\\
I_{3}=
\sigma_{xx}\sigma_{yy}\sigma_{zz}
+2\sigma_{xy}\sigma_{yz}\sigma_{zx}
-\sigma_{xx}\sigma_{yz}^{2}
-\sigma_{yy}\sigma_{zx}^{2}
-\sigma_{zz}\sigma_{xy}^{2}
$
応力の第1不変量
$I_{1}=\sigma_{1}+\sigma_{2}+\sigma_{3}$
は主応力の合計であるが、
応力テンソル成分で表せば、
$I_{1}=\sigma_{xx}+\sigma_{yy}+\sigma_{zz}$
となるから、$x,y,z$座標で表した直応力の合計でもある。
これを3で割って平均化した
$\sigma_{0}
=\frac{1}{3}(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})$
を平均直応力（等方応力）と呼ぶ。
（引張正で）四方八方から同じ圧力を受けている等方成分と考えておいてほしい。
このような等方成分のことを(材料力学等？の分野では）静水圧成分と言う場合もあるが、
水理学分野の静水圧は深さ方向の変化を考慮した圧力なので、
静水圧を圧力の等方成分の意味では使わないでおく。
金属の球体のような物体は、四方八方から同じ圧力を受けるぶんには、
なかなか塑性変形を生じない（こわれない）。
ということは、金属材料みたいなものが塑性変形で壊れるようなことを考える場合は、
平均直応力以外の成分を考えた方がいいのではないだろうか。
ということで、応力テンソルの直応力成分から平均直応力成分を取り除いた
以下のような偏差応力テンソル$\mathbf{[\sigma']}$を定義する。
$\mathbf{[\sigma']}
=
\left[
\begin{array}{ccc}
\sigma_{xx}-\sigma_{0} & \sigma_{xy} & \sigma_{zx} \\
\sigma_{xy} & \sigma_{yy}-\sigma_{0} & \sigma_{yz} \\
\sigma_{zx} & \sigma_{yz} & \sigma_{zz}-\sigma_{0}
\end{array}
\right]
$
応力テンソルから平均直応力成分を取り除いたせん断応力成分のようなものと
捉えておいていいだろう。
これは、$x,y,z$座標に依存した偏差応力だが、
材料が塑性したりということを考える際には、
どの方向に偏差応力成分が卓越するかはわからないので、
不変量みたいに座標に依存しない量を定義した方が便利だ。
そこで、さっき、応力テンソル$[\sigma]$に対して主応力を
求める3次方程式の係数として応力の第1, 第2, 第3不変量を定義したのと同じように、
偏差応力テンソル$[\sigma']$に対して主偏差応力を
求める3次方程式を考えれば、その係数として偏差応力の不変量を定義できそうだ。
上の式に
$\sigma_{0}
=\frac{1}{3}(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})$
を代入すると、偏差応力テンソルの各成分($\sigma_{xx}'$とか$\sigma_{xy}'$とか)は以下のように表される。
$\mathbf{[\sigma']}
=
\left[
\begin{array}{ccc}
\sigma_{xx}' & \sigma_{xy}' & \sigma_{zx}' \\
\sigma_{xy}' & \sigma_{yy}' & \sigma_{yz}' \\
\sigma_{zx}' & \sigma_{yz}' & \sigma_{zz}'
\end{array}
\right]
=
\left[
\begin{array}{ccc}
\frac{2\sigma_{xx}-\sigma_{yy}-\sigma_{zz}}{3}
& \sigma_{xy} & \sigma_{zx} \\
\sigma_{xy} &
\frac{2\sigma_{yy}-\sigma_{zz}-\sigma_{xx}}{3}
& \sigma_{yz} \\
\sigma_{zx} & \sigma_{yz} &
\frac{2\sigma_{zz}-\sigma_{xx}-\sigma_{yy}}{3}
\end{array}
\right]
$
上の主応力を求める3次方程式と同様に、
主偏差応力を求める3次方程式は、
スカラー変数を$\sigma'$と置くと、
以下のように表される。
$
\sigma'^{3}
-(
\sigma'_{xx}+\sigma'_{yy}+\sigma'_{zz}
)\sigma'^{2}
+
(
\sigma'_{xx}\sigma'_{yy}
+\sigma'_{yy}\sigma'_{zz}
+\sigma'_{zz}\sigma'_{xx}
-{\sigma'_{xy}}^{2}
-{\sigma'_{yz}}^{2}
-{\sigma'_{zx}}^{2}
)\sigma'
\\
-
(
\sigma'_{xx}\sigma'_{yy}\sigma'_{zz}
+2\sigma'_{xy}\sigma'_{yz}\sigma'_{zx}
-\sigma'_{xx}{\sigma'_{yz}}^{2}
-\sigma'_{yy}{\sigma'_{zx}}^{2}
-\sigma'_{zz}{\sigma'_{xy}}^{2}
)=0
$
この式の係数（を不変量として定義する目的で）以下のように置く。
$\sigma'^{3}-J_{1}\sigma'^{2}-J_{2}\sigma'-J_{3}=0$
符号が主応力の3次方程式と微妙に違っているが、
ただの習慣。
（主応力の式と符号を合わせて）
逆の符号で定義されている場合もあるかもしれない（特に応力の不変量の$I_{2}$とか）が、
その場合は係数の式が逆の符号で表されるということ。
まず$J_{1}$を
応力テンソル成分($\sigma_{xx}$とか$\sigma_{xy}$とか)で表そうと
計算してみると、上の行列の対角成分を足したものだから、
$J_{1}=0$となる。つまり、
主偏差応力を求める3次方程式は、
以下のように表されることになる。
$\sigma'^{3}-J_{2}\sigma'-J_{3}=0$
次に$J_{2}$を
応力テンソル成分($\sigma_{xx}$とか$\sigma_{xy}$とか)で表してみる。
$
-J_{2}=
\sigma'_{xx}\sigma'_{yy}
+\sigma'_{yy}\sigma'_{zz}
+\sigma'_{zz}\sigma'_{xx}
-{\sigma'_{xy}}^{2}
-{\sigma'_{yz}}^{2}
-{\sigma'_{zx}}^{2}
\\
=
\frac{1}{9}
(2\sigma_{xx}-\sigma_{yy}-\sigma_{zz})
(2\sigma_{yy}-\sigma_{zz}-\sigma_{xx})\\
+\frac{1}{9}
(2\sigma_{yy}-\sigma_{zz}-\sigma_{xx})
(2\sigma_{zz}-\sigma_{xx}-\sigma_{yy})\\
+\frac{1}{9}
(2\sigma_{zz}-\sigma_{xx}-\sigma_{yy})
(2\sigma_{xx}-\sigma_{yy}-\sigma_{zz})\\
-{\sigma_{xy}}^{2}
-{\sigma_{yz}}^{2}
-{\sigma_{zx}}^{2}
$
これをがんばって計算すると以下のように$J_{2}$が求まる。
${\displaystyle J_{2}=
\frac{1}{6}\left(
(\sigma_{xx}-\sigma_{yy})^{2}
+(\sigma_{yy}-\sigma_{zz})^{2}
+(\sigma_{zz}-\sigma_{xx})^{2}
+6{\sigma_{xy}}^{2}
+6{\sigma_{yz}}^{2}
+6{\sigma_{zx}}^{2}
\right)
}
$
この$J_{2}$は、偏差応力の第2不変量で座標に依存しない量だが、
「$J_{2}$流れ則」とか、塑性論ではよく使われる重要な量だ。
ちょっと（印象が変わるように？）書き直すと、
${\displaystyle J_{2}=
{\sigma_{xy}}^{2}
+{\sigma_{yz}}^{2}
+{\sigma_{zx}}^{2}
+\frac{
(\sigma_{xx}-\sigma_{yy})^{2}
+(\sigma_{yy}-\sigma_{zz})^{2}
+(\sigma_{zz}-\sigma_{xx})^{2}
}{6}
}
$
せん断応力成分の2乗和に、直応力成分どうしの差の2乗和の1/6を足したもので、
主要な成分としては、
せん断応力成分を(2乗にして絶対値にして)合計したような量だ。
これの$\sqrt{}$をとって応力の次元にした$\overline{\sigma}=\sqrt{J_{2}}$を
定義すると、$\overline{\sigma}$は、偏差応力のノルムみたいな量となり、
せん断抵抗を代表したような量と捉えられる。
ちなみに、$J_{2}$を主応力で表すと、以下のようになる。
${\displaystyle J_{2}=
\frac{
(\sigma_{1}-\sigma_{2})^{2}
+(\sigma_{2}-\sigma_{3})^{2}
+(\sigma_{3}-\sigma_{1})^{2}
}{6}
}
$
金属材料の降伏というのは、
平均直応力成分にはほとんど依存せず、偏差応力成分に依存するようだ。
そこで、様々な降伏条件というものがあるのだが、
よく使われる
フォン・ミーゼスの降伏条件というのは、
$\overline{\sigma}$がせん断降伏応力$\tau_{Y}$に達したときに
降伏するという降伏条件だ。
式で書くなら、
$\overline{\sigma}=\sqrt{J_{2}}=\tau_{Y}$ということだ。
条件式としては、$J_{2}-{\tau_{Y}}^{2}=0$と書かれることもある。
$yz$平面内で単純なせん断応力状態にあり、$\sigma_{yz}$のみが卓越して、
他の応力成分が無視できるような場合、
$\overline{\sigma}=\sqrt{J_{2}}=|\sigma_{yz}|$となるから、
その場合、$|\sigma_{yz}|$がせん断降伏応力$\tau_{Y}$に達すれば降伏することになる。
$J_{2}$のせん断応力成分は3成分の合計で、3で割って平均化されていないが、
平均化されていない方が、こういう意味では便利かもしれない。
さて、金属材料の降伏応力としては、測定しやすさから引張降伏応力がよく使われるが、
鋼棒みたいな1方向に長い金属材料を$z$軸に横たわらせ、
$z$軸方向に引っ張ったとすると、$\sigma_{zz}$の成分だけが卓越し、
他の成分はほとんど無視できるので、
$J_{2}=\frac{{\sigma_{zz}}^{2}}{3}$となり、
$\overline{\sigma}=\sqrt{J_{2}}=\frac{\sigma_{zz}}{\sqrt{3}}$となる。
どんどん棒を引っ張っていって、$\sigma_{zz}$が引張降伏応力$\sigma_{Y}$に
達したとすると、$\overline{\sigma}=\frac{\sigma_{Y}}{\sqrt{3}}$である。
つまり、$\sqrt{3}\overline{\sigma}$が引張降伏応力$\sigma_{Y}$に達すると、
降伏するということになる。
ということは、座標に依存しない（偏差応力のノルムみたいな量で）せん断抵抗を代表したような量として、
新たに
$\sigma_\text{eq}=\sqrt{3}\overline{\sigma}=\sqrt{3J_{2}}$
と定義すると、
$\sigma_\text{eq}$が引張降伏応力$\sigma_{Y}$に達した
(つまり$\sigma_\text{eq}=\sigma_{Y}$になった)ときに降伏すると判断できる。
この
$\sigma_\text{eq}=\sqrt{3}\overline{\sigma}=\sqrt{3J_{2}}$のことを
相当応力
と言う（構造力学公式集とかもこの定義）。
有限要素ツール等では、この相当応力のことを
ミーゼス応力(Mises stress)と呼んでいることもある。
一方で、$\sqrt{3}$をかけていない
$\overline{\sigma}=\sqrt{J_{2}}$のことを相当応力と言う場合もあるようなので、
そこは注意する必要がある。
FEMツールのミーゼス応力を出力する際は、
棒の引張を解析してみて、ミーゼス応力が、要素に与えた引張降伏応力にほぼ一致していれば、
$\sqrt{3J_{2}}$の方だし、要素に与えた引張降伏応力の$1/\sqrt{3}$ぐらいの値であれば、
$\sqrt{J_{2}}$の方だということになるだろう。
主偏差応力をちゃんと求めたらどうなるかとか、
その辺のもっとちゃんとした説明は、
私の恩師の岩熊先生と後輩の小山さんとの共著：
岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛--
計算機による構造解析の基礎としての構造力学を独習する』
の
9.2.1 降伏条件--状態の定義
の辺りを参照してください。
ちょっと、おまけ。
3軸圧縮試験の状態のときの相当応力$\sqrt{3J_{2}}$を考えてみる。
軸圧縮方向に最大主応力$\sigma_{1}$（土では圧縮が正）が生じていて、
側面の軸直角方向に中間主応力$\sigma_{2}=$
最小主応力$\sigma_{3}$が生じているとすると、上の主応力で表した$J_{2}$の式に
$\sigma_{2}=\sigma_{3}$を代入して、
${\displaystyle J_{2}=
\frac{
(\sigma_{1}-\sigma_{3})^{2}
}{3}
}
$
となり、相当応力$\sqrt{3J_{2}}=|\sigma_{1}-\sigma_{3}|$である。
つまり、3軸圧縮試験で測定した軸差応力$|\sigma_{1}-\sigma_{3}|$は、
相当応力に相当し、土のせん断抵抗を表しているということだろう。
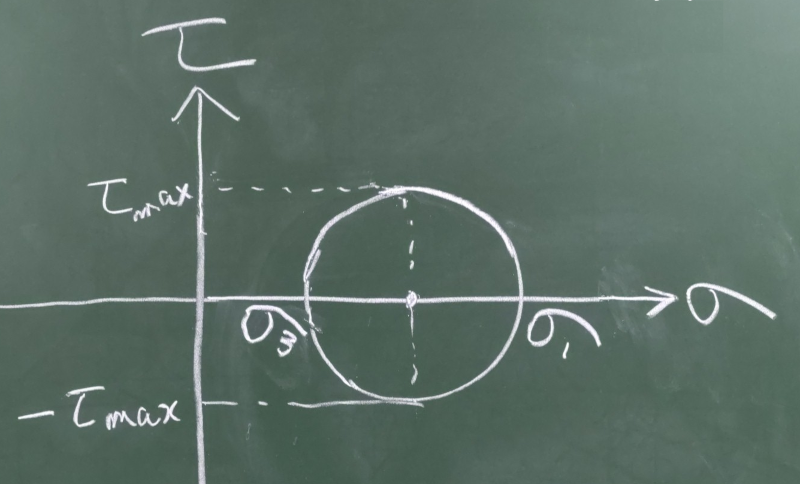
ちなみに、モールの応力円では、$\sigma$軸と円の交点
（せん断応力が$0$で直応力だけだから主応力）のうち、でっかい方（右側）が
（土だと圧縮が正で、最大主応力も、圧縮側の絶対値の
大きい順に$\sigma_{1}, \sigma_{2}, \sigma_{3}$ということだとすると）
$\sigma_{1}$で、
小さい方（左側）が$\sigma_{3}$ということだとすると、最大せん断応力は、円の半径なので
${\displaystyle \tau_{max}=\frac{\sigma_{1}-\sigma_{3}}{2}}$
となる。
トレスカの降伏条件（最大せん断応力説とも呼ばれる）は、この最大せん断応力がせん断降伏応力$\tau_{Y}$に
達したときに降伏するという考えで、
${\displaystyle \tau_{max}=\frac{\sigma_{1}-\sigma_{3}}{2}=\tau_{Y}}$
と表される。
