注意：
このページの数式は、
MathJaxを使って書いてます。
数式部分がおかしい場合は、更新ボタンをクリックすると
改善するかも知れません。
太文字のギリシャ文字($\mathbf{\sigma}$など)が、
太文字になっていない($\sigma$)かもしれません。
印刷版で確認して下さい。
その他、おかしい記述があると思ったら、
メールなどで指摘して下さい。
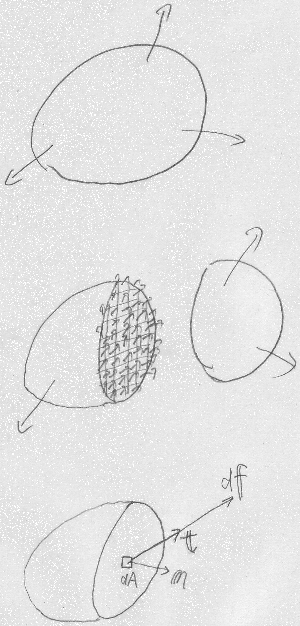物体にいくつかの外力が作用して変形してつりあっていたとする。
この物体の適当なところに切れ目を入れて平らな面で2つの部分に
切り分けたとする。
すると、
内力の節
で述べたように、
切断面には、切り離された部分だけで外力とのつりあいが成り立つような
内力が作用しなければならない。
内力の節
では、切断面に作用する内力を断面に直角な1つの力、
断面に平行な1つの力、1つのモーメントという具合に整理したけども、
実際の内力は断面のあらゆる点に分布して作用している。
力のつりあいだけが成り立てばいいなら、切断面に分布している内力を
図心に作用する$x,y,z$方向の力とモーメントとかに
まとめてしまってもいいかも知れないが、
切り離された物体の変形状態を保つ(例えば平らな切断面が
平らな状態を保つ)ようにするには、
切断面に分布している内力は、そのまま分布した状態で扱わないといけない。
そこで、
切断面のある微小部分にだけ着目し、面積$dA$の微小部分に作用する内力を、
(この微小範囲の内力の分布に関してはまとめてしまってもいいことにして)
1つの力$d\mathbf{f}$にまとめて表す。
この$d\mathbf{f}$を微小部分の面積$dA$で割って圧力の次元で表した
$\mathbf{t}=\frac{d\mathbf{f}}{dA}$
を表面力ベクトルという。
$\mathbf{t}$は、微小部分の内力を1つにまとめたものだから、
力の方向は座標方向とは一致しない。そこで、
座標方向との関係づけがやりやすいように、
微小部分から直角に突き出す単位法線ベクトルを
$\mathbf{n}$で表すことにする。
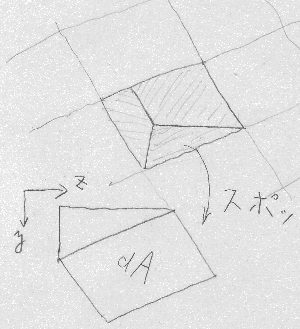さて、微小部分に座標軸と平行な切り込みを入れて、図のように
三角柱の積木状にスポッと切り出してみる。
以後、簡単のため、この積木を$yz$平面だけで考える。
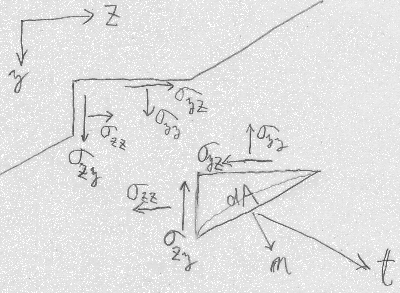切り出された直角な切断面($y$軸に直角な$y$面と$z$軸に直角な$z$面)には、
表面力ベクトル$\mathbf{t}$とつりあうような内力が作用しなければならない。
そこで、それぞれの面に作用する内力を単位面積当たりの力つまり圧力の
次元で$y$方向成分と$z$方向成分として与えることにする。
$y$面に作用する$y$方向の単位面積当たりの力は$\sigma_{yy}$,
$y$面に作用する$z$方向の単位面積当たりの力は$\sigma_{yz}$,
$z$面に作用する$z$方向の単位面積当たりの力は$\sigma_{zz}$,
$z$面に作用する$y$方向の単位面積当たりの力は$\sigma_{zy}$
という記号で書くことにする。
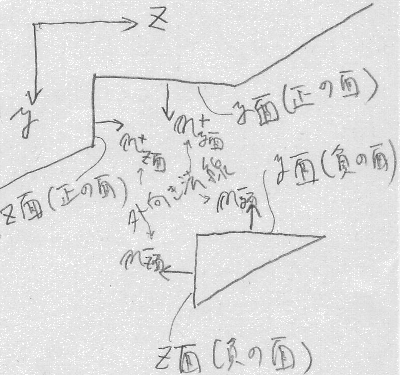力の正負の方向は、切断面から直角に突き出す(外向き)法線の向きが
座標の正の向きと一致する場合が正、逆向きの場合は負とする。
例えば切り出された三角形の直角をはさむ二面は、
外向き法線の向きが座標軸と逆になっている面(負の面)なので、
応力の正の向きは座標軸と逆向きになる。
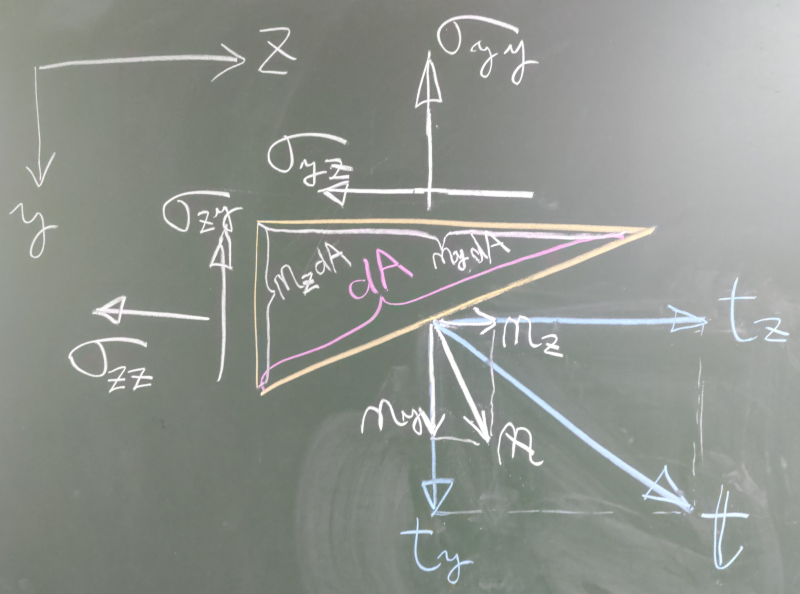さて、切り出された直角三角形の微小部分について力のつりあいを考えてみる。
まず、表面力ベクトル$\mathbf{t}$を$y$方向成分$t_{y}$と$z$方向成分$t_{z}$に
分解し、単位法線ベクトル$\mathbf{n}$も同様に
$n_{y}$と$n_{z}$に分解する。
直角三角形の積木の奥行き方向の厚さを簡単のため1とすると、
斜辺の長さは$\frac{dA}{1}=dA$となる。
残る2辺の長さは、単位法線ベクトルが作る直角三角形との相似関係から
$n_{z}:n_{y}$の比になることがわかる。
単位法線ベクトルの長さは1なので$n_{z}^{2}+n_{y}^{2}=1$だから、
3平方の定理から直角三角形の2辺の長さは、$n_{z}dA$, $n_{y}dA$となる。
単位面積当たりの力(圧力の次元)を力の次元にするには、
それぞれの力が作用している面の面積(奥行きが1だから辺の長さ)をかければよく、
したがって力のつりあいは以下のように書ける。
$y$方向の力のつりあい(下向き正):
$(+t_{y}dA)+(-\sigma_{yy}n_{y}dA)+(-\sigma_{zy}n_{z}dA)=0$
$z$方向の力のつりあい(右向き正):
$(+t_{z}dA)+(-\sigma_{yz}n_{y}dA)+(-\sigma_{zz}n_{z}dA)=0$
つまり、$dA$で割って移項すると、
$t_{y}=n_{y}\sigma_{yy}+n_{z}\sigma_{zy}$
$t_{z}=n_{y}\sigma_{yz}+n_{z}\sigma_{zz}$
と書けることになる。
この式を添字$i,j=y,z$を使って表現すると、
${\displaystyle t_{j}=\sum_{i=y,z}n_{i}\sigma_{ij}
\;\;\;\;(但しj=y,z)}$
と書ける。
このように2つの添字を使った配列$\sigma_{ij}$として表現できる
テンソル$[\mathbf{\sigma}]$を
応力テンソルと呼ひ、
$\sigma_{zz}, \sigma_{yz}$などの個々の成分を応力テンソル成分または
応力成分と呼ぶ。
3次元の場合には、
$t_{x}=n_{x}\sigma_{x x}+n_{y}\sigma_{yx}+n_{z}\sigma_{zx}$
$t_{y}=n_{x}\sigma_{xy}+n_{y}\sigma_{yy}+n_{z}\sigma_{zy}$
$t_{z}=n_{x}\sigma_{xz}+n_{y}\sigma_{yz}+n_{z}\sigma_{zz}$
まとめると
${\displaystyle t_{j}=\sum_{i=x,y,z}n_{i}\sigma_{ij}\;\;\;\;
(但しj=x,y,z)}$
となる。
添字を用いた総和演算や行列表示がわかりやすくなるように、
$i,j=x,y,z$を$i,j=1,2,3$に置き換えて($\sigma_{yz}$などを
$\sigma_{23}$などと)表記するなら、
${\displaystyle t_{j}=\sum_{i=1}^{3}n_{i}\sigma_{ij}\;\;\;\;
(但しj=1,2,3)}$
となる。
ちなみに、添字の多いテンソルの式を表記する際に、
総和記号$\sum$は省略して、同じ添字が2つ以上あった場合(この場合の$i$とか)には、
その添字について和を取るという表記法
(アインシュタイン規約とか総和規約と呼ばれる)
で表記されることも多いので、一応、覚えておいてほしい。
アインシュタイン規約に慣れると、配列計算のプログラムも
書きやすくなるかも知れない。
ちなみに、上の式をアインシュタイン規約で書くと、
$t_{j}=n_{i}\sigma_{ij}\;\;\;\;
(但しi,j=1,2,3)$
となる。
ひずみテンソルの場合と同様に、
応力テンソル$\mathbf{\sigma}$を行列で表示するなら、
$[\mathbf{\sigma}]
=
\left[
\begin{array}{ccc}
\sigma_{x x} & \sigma_{xy} & \sigma_{xz} \\
\sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\
\sigma_{zx} & \sigma_{zy} & \sigma_{zz}
\end{array}
\right]
$
と表せる。
応力テンソル成分$\sigma_{ij}$もひずみテンソル成分$\varepsilon_{ij}$と
同様に対称行列になっているということについては、
下の応力のつりあいのところで示す。
応力成分$\sigma_{ij}$のうち、切断面に直角な成分
($i=j$となる$\sigma_{x x}, \sigma_{yy}, \sigma_{zz}$)を
直応力と呼び、
切断面に平行な成分($i\ne j$となる$\sigma_{xy}, \sigma_{yz}, \sigma_{zx},
\sigma_{yx}, \sigma_{zy}, \sigma_{xz}$)
をせん断応力と呼ぶ。
直応力やせん断応力を特に区別しない場合は単に応力と呼ぶ。
応力の次元は定義から分かるように
圧力(力/面積)の次元で、単位は
N/m2やPaなどで表される。
SI単位の接頭語(k, M, Gなど)は、
原則として先頭に1個だけつけて、分母にはつけないことが望ましいとされているので、
kN/m2, kPa, MPa, GPa などを使うのが推奨されるであろう。
もっとも、土木などの分野では、kN/mm2
や工学単位系のkgf/mm2
などの表記もまだ習慣的に使われることがある。
例えば、平成14年度版の道路橋示方書では、N/mm2が使われている。
梁の問題では、切断面に作用する内力を軸力や曲げモーメントなどの
断面力で
与えるが、こうした断面力は
(後で詳しく述べるが)
軸方向の直応力を断面に対して積分して合計することで求めることができる
(曲げモーメントは、圧縮側と引張側の方向を考慮して腕の長さをかけながら
積分すればいいが、「せん断力」はちょっと特殊なのでこれについては
後述)。
このように断面力は断面に作用する応力を合計したものという意味合いで
「合応力」と呼ばれることもある。
合応力は応力ではなく
断面力だから、次元は「力」だったり「力×長さ」だったりする。
さて、
土木や建築の分野では、
上記の「応力」の意味で「応力度」という語を用い、
上記の「合応力」の意味で「応力」という語を用いるという
使い分けをする紛らわしい習慣が一部にある
(
例えば、平成14年度版の道路橋示方書でも「応力度」という表現が
使われ続けている
)。
「応力」を圧力の次元を持つ応力テンソル成分の意味で使うのが
物理の分野の一般的な使い方だと思うので、
このテキストでも「応力」は圧力の次元を持つ応力テンソル成分の
意味で用いることとし、「応力度」といった紛らわしい表現は使わない。
「ひずみ度」についてはひずみ-変位関係参照。
物体内部の任意の微小部分を切り取って考える場合、
その微小部分の切断面に作用する応力はつりあっていないといけない。
各辺が座標軸と平行になるような直方体(2次元で考えるなら長方形)の
微小要素を切り出してみる。
まず、図の点$A$をはさむ2辺の切断面については、
応力テンソルの節の三角形の積木の切断面と同様に
作用する応力を定義する。
つまり、
$y$面に作用する$y$方向の応力は$\sigma_{yy}$,
$y$面に作用する$z$方向の応力は$\sigma_{yz}$,
$z$面に作用する$z$方向の応力は$\sigma_{zz}$,
$z$面に作用する$y$方向の応力は$\sigma_{zy}$
とし、応力の正負の方向は、切断面から直角に突き出す(外向き)法線の向きが
座標の正の向きと一致する場合が正、逆向きの場合は負とする。
例えば点$A$をはさむ2面は、
外向き法線の向きが座標軸と逆になっている面(負の面)なので、
応力の正の向きは座標軸と逆向きになる。
点$A$をはさむ2面のむかい側の2面に作用する応力は、
長方形の縦横の長さ$dy,dz$がそれぞれ0とみなせるぐらいに微小なら、
向かい合う面の応力とつりあうような逆向きの応力ということにしても
いいかも知れないが、
ここでは、ある点の応力とそこから$dy$や$dz$離れた地点の応力とは
同じとはみなせないことにしておく。
そこで、ひずみテンソル$\varepsilon_{ij}$
と同様に応力テンソル$\sigma_{ij}$も任意点$(x,y,z)$の関数として
与えられると考えることにする。
といっても、応力テンソルは、確か物体を半分に切った切断面から切り出した
微小な三角柱の積木の表面に対して定義したのであって、
点に対して定義した訳ではないはずではなかったかと言われるかも知れないが、
まあ、そこは微小な三角柱は十分に微小で例えばその重心とかの点に
対して各応力成分が定義されているのだと考えてほしい。
で、今 考えている微小な長方形要素の点$A$をはさむ2面に作用する応力成分は、
例えばこの長方形の図心の「点」に対して定義されたものだということにしておいて、
点$A$の向かい側の2面に作用する応力は、
この長方形要素に隣り合う長方形要素の図心点について定義されたものだというふうに
でも考えてほしい。
すると、例えばこの長方形要素の左端の面では$\sigma_{zz}$の値を取る直応力が、
そこから$dz$離れた右端の面では$\sigma_{zz}$からどれだけ変化するかの
変化量は、$\sigma_{zz}$を$z$の関数とみなして
$z$方向の瞬間の変化率$\frac{\partial\sigma_{zz}}{\partial z}$
に$dz$をかけて、
$\frac{\partial \sigma_{zz}}{\partial z}dz$と表すことができそうだ
(微分が偏微分になっているのは$\sigma_{zz}$が$x,y,z$の関数だから)。
つまり、右端の面の直応力は、
$\sigma_{zz}+\frac{\partial \sigma_{zz}}{\partial z}dz$と表すことができそうだ。
他の応力成分についても同じように考えていけば、
点$A$の向かい側の2面について
図のような応力が作用していると考えられる。
さて、これらの作用応力に対して力のつりあいを考えてみる。
この長方形要素というか奥行きを考えると直方体要素の
奥行きの長さが1だとすると、
各面に作用している応力に作用面の(長方形として見た場合は)辺の長さ
(と1)をかければ、作用している力が求まる。よって、
$y$方向のつりあい(下向き正):
$
(-\sigma_{zy}dy)+(-\sigma_{yy}dz)
+\{+(\sigma_{zy}+\frac{\partial\sigma_{zy}}{\partial z}dz)dy\}
+\{+(\sigma_{yy}+\frac{\partial\sigma_{yy}}{\partial y}dy)dz\}
=0
$
$z$方向のつりあい(右向き正):
$
(-\sigma_{zz}dy)+(-\sigma_{yz}dz)
+\{+(\sigma_{zz}+\frac{\partial\sigma_{zz}}{\partial z}dz)dy\}
+\{+(\sigma_{yz}+\frac{\partial\sigma_{yz}}{\partial y}dy)dz\}
=0
$
となるが、$+-$で相殺される項を消して$dydz$で割ると、応力のつりあいは、
$y$方向のつりあい:
$
\frac{\partial\sigma_{yy}}{\partial y}
+\frac{\partial\sigma_{zy}}{\partial z}
=0$
$z$方向のつりあい:
$
\frac{\partial\sigma_{yz}}{\partial y}
+\frac{\partial\sigma_{zz}}{\partial z}
=0$
と書ける。これを添字$i,j=1,2,3$を使って3次元について整理すると、
${\displaystyle \sum_{i=1}^{3}\frac{\partial\sigma_{ij}}{\partial x_{i}}=0
\;\;\;\;(但しj=1,2,3)}$
と書ける。
但し、$x_{1}=x, x_{2}=y, x_{3}=z$である。
さて、次にモーメントのつりあいを考える。
点$A$回りのモーメントのつりあい(左まわり正):
$-(\sigma_{zz}dy)\cdot\frac{dy}{2}$ 左端直応力による
$+(\sigma_{yy}dz)\cdot\frac{dz}{2}$ 上端直応力による
$+\{(\sigma_{zz}+\frac{\partial\sigma_{zz}}{\partial z}dz)dy\}\cdot\frac{dy}{2}$
右端直応力による
$-\{(\sigma_{zy}+\frac{\partial\sigma_{zy}}{\partial z}dz)dy\}\cdot dz$
右端せん断応力による
$-\{(\sigma_{yy}+\frac{\partial\sigma_{yy}}{\partial y}dy)dz\}\cdot\frac{dz}{2}$
下端直応力による
$+\{(\sigma_{yz}+\frac{\partial\sigma_{yz}}{\partial y}dy)dz\}\cdot dy$
下端せん断応力による
$=0 $
$+-$で相殺される項を消して$dzdy$で割ると、
$\frac{\partial\sigma_{zz}}{\partial z}\frac{dy}{2}$
$-(\sigma_{zy}+\frac{\partial\sigma_{zy}}{\partial z}dz)$
$-\frac{\partial\sigma_{yy}}{\partial y}\frac{dz}{2}$
$+(\sigma_{yz}+\frac{\partial\sigma_{yz}}{\partial y}dy)$
$=0$
2010/5/17まで、まちがって右端せん断応力による項と下端せん断応力による項に
$\frac{1}{2}$をかけてしまって
(そうすると$y, z$方向の力のつりあいの項ができてしまうのを
利用して微小項を削除して)いました。
大変、失礼しました。
$d$の1次の微小項を削除すると、
$
-\sigma_{zy}
+\sigma_{yz}
=0$
つまり、
$\sigma_{yz}=\sigma_{zy}$
となる。$xy$面、$zx$面についても
同様にモーメントのつりあいを考えれば、3次元でのモーメントのつりあいは、
$\sigma_{ij}=\sigma_{ji}\;\;\;\;(但しi,j=x,y,z)$
と書ける。ひずみテンソル成分
$\varepsilon_{ij}$の場合は、
伸びひずみと
せん断ひずみの定義から
対称行列になっていたが、
応力テンソル成分$\sigma_{ij}$は、モーメントのつりあいから対称行列となる。
2020/11/6追記
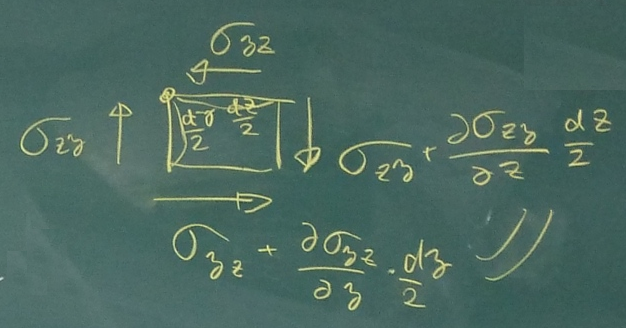上のモーメントのつりあいに
$dy=\frac{dy}{2}+\frac{dy}{2}$
と
$dz=\frac{dz}{2}+\frac{dz}{2}$
を代入して変形すると、
$(
\frac{\partial\sigma_{yz}}{\partial y}
+
\frac{\partial\sigma_{zz}}{\partial z}
)\cdot\frac{dy}{2}$
$-(\sigma_{zy}+\frac{\partial\sigma_{zy}}{\partial z}\cdot\frac{dz}{2})$
$-(
\frac{\partial\sigma_{yy}}{\partial y}
+
\frac{\partial\sigma_{zy}}{\partial z}
)\cdot\frac{dz}{2}$
$+(\sigma_{yz}+\frac{\partial\sigma_{yz}}{\partial y}\cdot\frac{dy}{2})$
$=0$
応力のつりあい
$
\frac{\partial\sigma_{yy}}{\partial y}
+
\frac{\partial\sigma_{zy}}{\partial z}
=0$
$
\frac{\partial\sigma_{yz}}{\partial y}
+
\frac{\partial\sigma_{zz}}{\partial z}
=0$
を代入すると、1行目と3行目が消えるから、
$\sigma_{yz}+\frac{\partial\sigma_{yz}}{\partial y}\cdot\frac{dy}{2}
=
\sigma_{zy}+\frac{\partial\sigma_{zy}}{\partial z}\cdot\frac{dz}{2}$
という関係が得られる。まあ、ここで(分子と分母に$\partial$があるのは1のオーダーとして)
$d$の一次の項を消せば、$\sigma_{yz}=\sigma_{zy}$ということでもいいのだが、
これは、縦$\frac{dy}{2}$, 横$\frac{dz}{2}$の微小部分の
下の切断面と右の切断面に作用するせん断応力どうしが等しいという関係でもある。
写真の
$\frac{\partial\sigma_{yz}}{\partial y}\cdot\frac{dy}{2}$
のところが、2023/11/9まで
$\frac{\partial\sigma_{yz}}{\partial z}\cdot\frac{dy}{2}$
になってました。すいません。
2021/4/23追記
1次の微小項を消さずに$\sigma_{yz}=\sigma_{zy}$を示せないかという
ことであれば、
上の追記で、微小部分の下の切断面と右の切断面に作用するせん断応力が
等しいということは、
この同じ微小部分に対して、座標軸を上向きと左向きを正にとって同じ
導出をすれば、上の切断面と左の切断面のせん断応力が等しいという
結論になる。だから$\sigma_{yz}=\sigma_{zy}$という理屈では、
ちょっと詭弁っぽいだろうか。
さて、物体の任意点の変形を
ひずみテンソルとして定義できたし、
物体の任意点の内力を
応力テンソルとして定義できた訳だけど、
この応力とひずみとを関係づけるにはどうしたらいいだろうか。
我々が(中学や高校の理科や物理の範囲で)知っている物体の弾性に関する
法則を応力テンソルやひずみテンソルを用いてもっと一般的に
表現したらどういうふうに
表現できるだろうか。
『物理I』(東京書籍、平成18年2月10日発行)p.157によると、
「ばねに力を加え変形させたあと，力を除くと変形がもとに完全に
もどる場合，この変形を弾性変形という。」
とあり、注釈部分には
「これに対して，力をとりのぞいても変形が残るような場合を
塑性変形という。」
なんてことまでちゃんと書いてある。
塑性変形が生じない範囲の外力を受ける場合、
ばねに限らず、一般的な物体(木材とかプラスチックとか金属とか)では、
ある外力の組み合わせに対しては同じ変形状態になる。
外力を取り除けば、外力が作用していなかった初期状態に戻るし、
また同じ外力を加えれば、同じ変形状態になる。
つまり、外力の状態と変形の状態とが1対1に対応している。
こういう(木材とかプラスチックとか金属とかの)物体の一般的な性質のことを弾性と呼んでいるのだが、
外力の状態と物体の任意点の変形とをいきなり対応づけるのは難しい。
その点、外力を受けた際に物体内部に生じる
内力であれば、
任意点$(x,y,z)$での応力テンソルの9成分で表せるから、
任意点$(x,y,z)$でのひずみテンソル9成分と成分の数も同じだし、
それらが1対1で対応しているという関係を式で表現できそうだ。
つまり、「ある点の応力テンソル9成分が分かれば、その点のひずみテンソル9成分が
決まる」あるいは「ある点のひずみテンソル9成分が分かればその点の
応力テンソル9成分が決まる」のどちらかを式で表現したいのだが、
ここでは、後者の表現を用いるとすると、それはたぶん
「応力テンソル成分$\sigma_{ij}$が座標$(x,y,z)$と
ひずみテンソル成分$\varepsilon_{ij}$の関数として与えられる」
ということなのだが、
座標$(x,y,z)$とひずみテンソル成分$\varepsilon_{ij}$の関数として与えられる
4階のテンソル$E_{ijk\ell}$を用いると、その関係は、
${\displaystyle \sigma_{ij}=\sum_{k=1}^{3}\sum_{\ell=1}^{3}E_{ijk\ell}\varepsilon_{k\ell}
\;\;\;\;(但しi,j,k,\ell=1,2,3)}$
と表せる。$a_{ij}$みたいな2階のテンソルなら$i$行$\times j$列の
行列として表せるけど、4階のテンソルになると、紙の上で表現するのは
難しくなるが、$i\times j\times k\times \ell=3\times 3\times 3\times 3=81$
の81成分のテンソルとういことになる。
ちなみにアインシュタイン規約で書くと、
$\sigma_{ij}=E_{ijk\ell}\varepsilon_{k\ell}
\;\;\;\;(但しi,j,k,\ell=1,2,3)$
となる。
この4階のテンソル$E_{ijk\ell}$のことを弾性係数テンソルという。
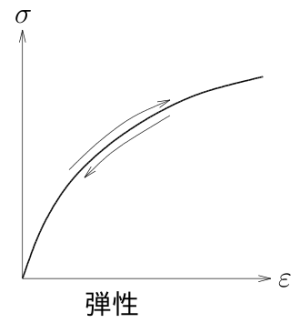さて、一応、上式で関連づけた応力テンソルとひずみテンソルのそれぞれ
適当な1つの成分どうしの関係をグラフに書くなら、図のような感じになる。
応力とひずみが1対1に対応していて、
応力を加えて取り除くと、同じ経路上を戻ってくる。
さて、我々が知っている(木材とかプラスチックとか金属とかの)一般的な物質は、
単に弾性が
あるだけではなく、外力と変形との関係が比例関係にあることも分かっている。
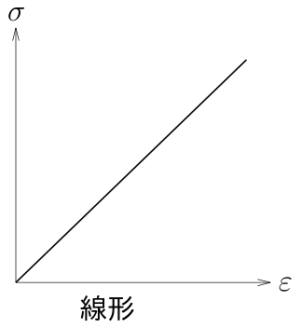比例関係というのは、グラフに書くと直線になるので線形というが、
ちなみに、弾性だからといって線形だとは限らないし(力を
取り除くと元に戻るけど、力と変形の関係は線形じゃない非線形弾性もあるし)、
線形だからといって弾性だとは限らない
(力と変形の関係は線形だけど力を取り除いても元に戻らない
線形非弾性もあり得る)ので混同しないように。
さて、(木材とかプラスチックとか金属とかの)一般的な物質の塊から$x,y,z$軸方向にそれぞれ細長い棒を
切り出して引っ張り試験をしてみれば、それぞれの方向の直応力と
伸びひずみが線形関係にあることが確かめられるし、
ねじり試験をしてみれば、それぞれの方向のせん断応力とせん断ひずみが
線形関係にあることも確かめられる。
それ以外のある方向の応力成分とある方向のひずみ成分との組み合わせでも
適当な試験を行えば線形関係があることが確かめられるのではないかと
思う(たぶん)。
$x$と$y$が線形関係にあることを式で表すには、
$y=ax$みたいに$x$に定数$a$をかけて$y$と等値すればいいが、
どの応力テンソル成分もどのひずみテンソル成分とも線形関係にあることを
式で表すには、上の弾性係数テンソル$E_{ijk\ell}$の81個の成分がすべて
定数であればよい。
という訳で、ここでは木材とかプラスチックとか金属のような物質を扱うことにして、
$E_{ijk\ell}$の各成分は定数だということにすると、
$\sigma_{ij}=E_{ijk\ell}\varepsilon_{k\ell}
\;\;\;\;(但しi,j,k,\ell=1,2,3)$
の式は一般化されたフックの法則と呼ばれる。
さて、
応力テンソル成分$\sigma_{ij}$と
ひずみテンソル成分$\varepsilon_{k\ell}$は、
それぞれ対称で、$\sigma_{ij}=\sigma_{ji}$,
$\varepsilon_{k\ell}=\varepsilon_{\ell k}$だから、
$E_{ijk\ell}$
の添字$ij$を$ji$と取り換えたものは同じだし、
$k\ell$を$\ell k$と取り換えたものも同じである。
すると$i,j$の組み合わせは6通りだし、
すると$k,l$の組み合わせも6通りだから、
$E_{ijk\ell}$の独立な成分は$6 \times 6=36$個でいいことになる。
応力テンソルとひずみテンソルの成分が6成分ずつだったら、
1列に並べてベクトルで書いてもそれほど長くならないので、
以下のように$6\times 6$の行列で関係づけられる。
$
\left(
\begin{array}{c}
\sigma_{x x} \\
\sigma_{yy} \\
\sigma_{zz}\\
\sigma_{xy}\\
\sigma_{yz}\\
\sigma_{zx}
\end{array}
\right)
=
\left[
\begin{array}{cccccc}
E_{11} & E_{12} & E_{13} & E_{14} & E_{15} & E_{16} \\
E_{21} & E_{22} & E_{23} & E_{24} & E_{25} & E_{26} \\
E_{31} & E_{32} & E_{33} & E_{34} & E_{35} & E_{36} \\
E_{41} & E_{42} & E_{43} & E_{44} & E_{45} & E_{46} \\
E_{51} & E_{52} & E_{53} & E_{54} & E_{55} & E_{56} \\
E_{61} & E_{62} & E_{63} & E_{64} & E_{65} & E_{66}
\end{array}
\right]
\left(
\begin{array}{c}
\varepsilon_{x x}\\
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{xy}\\
\varepsilon_{yz}\\
\varepsilon_{zx}
\end{array}
\right)
$
さて、ここから先はまだまだ遠いので、この辺から適当にごまかし始めるが、
ひずみエネルギー密度関数
$W=\frac{1}{2}E_{ijk\ell}\varepsilon_{ij}\varepsilon_{k\ell}$というもの
が存在してある条件
($\sigma_{ij}=\frac{\partial W}{\partial\varepsilon_{ij}}$)
を満たすと($W$がポテンシャルで$\sigma_{ij}$が保存力として表せるみたいな
条件と対応し、$E_{ijkl}=E_{klij}$の対称性がなりたち)
$E_{ijk\ell}$の独立な成分は21個に減り、
互いに直交する3面に対して対称性を有す(木材のような)
直交異方性材料だと
$E_{ijk\ell}$の独立な成分は9個となる。
応力テンソル成分の重複する対称成分を取り除いた6成分
($\sigma_{x x}, \sigma_{yy}, \sigma_{zz}, \sigma_{xy}, \sigma_{yz}, \sigma_{zx}$)
と
ひずみテンソル成分の重複する対称成分を取り除いた6成分
($\varepsilon_{x x}, \varepsilon_{yy}, \varepsilon_{zz}, \varepsilon_{xy}, \varepsilon_{yz}, \varepsilon_{zx}$)
との関係を
$6\times 6$の行列を用いて関係づけると、以下のように書ける。
各成分の物理的な意味は、
これの逆関係の方がわかりやすい。
保存力と対称性の話をちょっとだけ。$U$という関数に対して、
$F_{x}=-\frac{\partial U}{\partial x}$,
$F_{y}=-\frac{\partial U}{\partial y}$,
$F_{z}=-\frac{\partial U}{\partial z}$
みたいに定義できる力$F$のことを保存力と呼び、こういうふうに表せる
$U$のことをポテンシャル（位置エネルギー）と呼ぶ。
そうすると、
$\frac{\partial F_{x}}{\partial y}=\frac{\partial F_{y}}{\partial x}$,
$\frac{\partial F_{y}}{\partial z}=\frac{\partial F_{z}}{\partial y}$,
$\frac{\partial F_{z}}{\partial x}=\frac{\partial F_{x}}{\partial z}$
がなりたつことが$F$が保存力であることの条件となる。
$
\left(
\begin{array}{c}
\sigma_{x x} \\
\sigma_{yy} \\
\sigma_{zz}\\
\sigma_{xy}\\
\sigma_{yz}\\
\sigma_{zx}
\end{array}
\right)
=
\left[
\begin{array}{cccccc}
E_{11} & E_{12} & E_{13} & 0 & 0 & 0\\
E_{12} & E_{22} & E_{23} & 0 & 0 & 0\\
E_{13} & E_{23} & E_{33} & 0 & 0 & 0\\
0 & 0 & 0& E_{44} & 0 & 0 \\
0 & 0 & 0 & 0& E_{55} & 0 \\
0 & 0 & 0 & 0 & 0& E_{66} \\
\end{array}
\right]
\left(
\begin{array}{c}
\varepsilon_{x x}\\
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{xy}\\
\varepsilon_{yz}\\
\varepsilon_{zx}
\end{array}
\right)
$
更に、プラスチックや金属のようにあらゆる方向に対称面を持つ等方性材料では
独立な成分は2個だけになる。
$G$と$\nu$という2個の定数を使って
$6\times 6$の行列の部分を書き換えると、以下のように書ける。
$
\left(
\begin{array}{c}
\sigma_{x x} \\
\sigma_{yy} \\
\sigma_{zz}\\
\sigma_{xy}\\
\sigma_{yz}\\
\sigma_{zx}
\end{array}
\right)
=
{\displaystyle \frac{2G}{1-2\nu}}
\left[
\begin{array}{cccccc}
1-\nu& \nu& \nu& 0& 0& 0\\
\nu& 1-\nu& \nu& 0& 0& 0\\
\nu& \nu& 1-\nu& 0& 0& 0\\
0&0&0&1-2\nu& 0& 0\\
0&0&0&0& 1-2\nu& 0\\
0&0&0& 0&0& 1-2\nu
\end{array}
\right]
\left(
\begin{array}{c}
\varepsilon_{x x}\\
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{xy}\\
\varepsilon_{yz}\\
\varepsilon_{zx}
\end{array}
\right)
$
このように関係づけられる$G$のことをせん断弾性係数と言い、
$\nu$のことをポアソン比と言う
(もっとわかりやすい物理的な意味との対応は後述)。
ちなみに、
等方性材料では$E=2G(1+\nu)$とおいた$E$をヤング率と言う
(ヤング率のもっとわかりやすい物理的意味との対応は後述)。
さて、上の式の行列の逆行列を求めれば、ひずみについての表現で
以下のように書くこともできる。
$
\left(
\begin{array}{c}
\varepsilon_{x x}\\
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{xy}\\
\varepsilon_{yz}\\
\varepsilon_{zx}
\end{array}
\right)
=
{\displaystyle \frac{1}{E}}
\left[
\begin{array}{cccccc}
1& -\nu& -\nu& 0& 0& 0\\
-\nu& 1& -\nu& 0& 0& 0\\
-\nu& -\nu& 1& 0& 0& 0\\
0&0&0&1+\nu& 0& 0\\
0&0&0&0& 1+\nu& 0\\
0&0&0& 0&0& 1+\nu
\end{array}
\right]
\left(
\begin{array}{c}
\sigma_{x x}\\
\sigma_{yy}\\
\sigma_{zz}\\
\sigma_{xy}\\
\sigma_{yz}\\
\sigma_{zx}
\end{array}
\right)
$
ちなみに、せん断応力成分
$\sigma_{xy}, \sigma_{yz}, \sigma_{zx}$
は、
$\tau_{xy}, \tau_{yz}, \tau_{zx}$の記号で書かれることも多い。
もし、せん断ひずみ成分
$\varepsilon_{xy}, \varepsilon_{yz}, \varepsilon_{zx}$
が、
$\gamma_{xy}, \gamma_{yz}, \gamma_{zx}$
という記号で書かれていたら、
工学せん断ひずみ
成分で書かれている可能性が高い。
その場合、せん断応力とせん断ひずみとを関係づける係数は
2倍または$\frac{1}{2}$にする必要があるので注意が必要である。
例えば、上のせん断応力とせん断ひずみの関係式だけを抜き出すと
$\tau_{xy}=2G\varepsilon_{xy}$
$\tau_{yz}=2G\varepsilon_{yz}$
$\tau_{zx}=2G\varepsilon_{zx}$
となるが、これを工学せん断ひずみ成分で書くと
$\tau_{xy}=G\gamma_{xy}$
$\tau_{yz}=G\gamma_{yz}$
$\tau_{zx}=G\gamma_{zx}$
となる。
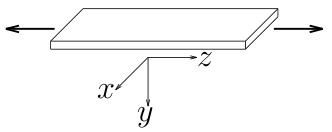例えば、薄い板を細長く切り出して、
細長い方向に引っ張るような問題を考える場合、
板厚方向を$y$, 細長い方向を$z$とすると、
$\sigma_{zz}$以外の応力成分は無視できるような状態になるので、
上の直ひずみと直応力の関係式
に$\sigma_{xx}=\sigma_{yy}=\sigma_{xy}=\sigma_{yz}=\sigma_{zx}=0$を代入すると、
$
\left(
\begin{array}{c}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\varepsilon_{zz}
\end{array}
\right)
=
\frac{1}{E}
\left(
\begin{array}{rrr}
1 & -\nu & -\nu \\
-\nu & 1 & -\nu \\
-\nu & -\nu & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
0\\
0\\
\sigma_{zz}
\end{array}
\right)
$
$\varepsilon_{xy}=\varepsilon_{yz}=\varepsilon_{zx}=0$
から、
$\varepsilon_{x x}=-\frac{\nu\sigma_{zz}}{E}$
$\varepsilon_{yy}=-\frac{\nu\sigma_{zz}}{E}$
$\varepsilon_{zz}=\frac{\sigma_{zz}}{E}$
となるから、これらを整理して、
$\sigma_{zz}=E\varepsilon_{zz}$
$\nu=-\frac{\varepsilon_{x x}}{\varepsilon_{zz}}=
-\frac{\varepsilon_{yy}}{\varepsilon_{zz}}$
という関係が得られる。
$\sigma_{zz}=E\varepsilon_{zz}$は1次元のフックの法則である。
土木の学部の範囲の話では、
直応力と直ひずみの関係は、ほぼ、この1次元のフックの法則だけで
話が済んでしまうが、
それはあくまで、
例えば、梁のような細長い棒を扱っているとか、
コンクリートや土質の円柱状の試験体みたいなものを一様に均等に圧縮しているとか、
1次元のフックの法則がなりたつような条件で議論しているから
ということを忘れてはいけない。
$\nu=-\frac{\varepsilon_{xx}}{\varepsilon_{zz}}$
または
$\nu=-\frac{\varepsilon_{yy}}{\varepsilon_{zz}}$
はポアソン比である。
$z$方向に長い試験体を$z$方向に引っ張った場合、
$z$方向を縦方向、その直角方向を横方向と言い、
縦方向の直ひずみを縦ひずみ、横方向の直ひずみを横ひずみと言うが、
縦ひずみに対する横ひずみの比がポアソン比となる。
マイナスがついているが、
直ひずみは引張が正なので、細長い棒を引っ張った場合は、
縦ひずみは引っ張られる方向なので正になり、
横ひずみは縮む方向なので負になり、
ポアソン比の値としては正になる。
コンクリート供試体みたいなものを圧縮したときは、これの逆で、
圧縮してる側の縦ひずみは負になり、
横ひずみは膨れて正になるので、やはりポアソン比の値としては正になる。
ちなみに3年次の土木環境工学実験の構造実験では、
この
$\sigma_{zz}=E\varepsilon_{zz}$を使ってヤング率を測定し、
$\nu=-\frac{\varepsilon_{yy}}{\varepsilon_{zz}}$を使って
ポアソン比を求める。
ポアソン比の定義から考えると、
例えば、円柱状の材料に一様な圧縮をかけているのに、
横方向に全く膨れない（横ひずみがない）とすれば、
ポアソン比は0となる。
例えば、コルクとかスポンジみたいな材料だと、
縦に押されても横方向にほとんど膨れないので、ポアソン比は0に近くなる。
つまり、ポアソン比の最小値は0ということだ。
では、ポアソン比の最大値はどうなるだろうか。
一般的な材料では、縦に圧縮されると、縦方向に縮むので、
縦に押されて減った体積のぶんだけ横に膨れるということにはならない。
しかし、例えば水みたいに圧縮されてもほとんど縮まない材料の場合は、
縦に押されて縦方向に縮むと、その縮んだ体積のぶんだけ横に膨れてしまう。
こういう状態がポアソン比の最大値だ。
ちなみにこの最大値は0.5だが、
なぜそうなるかに興味のある人は、この辺参照。
ちなみに、木材とか内部構造を持つ材料の場合は、
測定方法によってはポアソン比が0.5を超えたりすることもある。
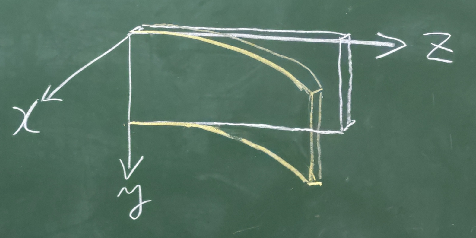薄い板を対象とするような問題の場合、板厚方向の応力成分が、
それ以外の方向の応力成分に比べて無視できるような近似ができる状態を
平面応力状態と呼ぶ。例えば、板厚方向に$x$軸を取ると、
$\sigma_{xx}=\sigma_{xy}=\sigma_{zx}=0$
とみなせる状態のことである。
覚え方は「応力を無視したのが平面応力」。
ただし、$x$方向の直ひずみ$\varepsilon_{xx}$は無視できない。
上の
ひずみ-応力関係の式に、
$\sigma_{xx}=\sigma_{xy}=\sigma_{zx}=0$
を代入すると以下のようになる。
$
\left(
\begin{array}{c}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{yz}
\end{array}
\right)
=
{\displaystyle \frac{1}{E}}
\left[
\begin{array}{cccccc}
1& -\nu& -\nu& 0\\
-\nu& 1& -\nu& 0\\
-\nu& -\nu& 1& 0\\
0&0&0&1+\nu
\end{array}
\right]
\left(
\begin{array}{c}
0 \\
\sigma_{yy}\\
\sigma_{zz}\\
\sigma_{yz}
\end{array}
\right)
$
$\varepsilon_{xy}=0$
$\varepsilon_{zx}=0$
$\varepsilon_{xx}={\displaystyle -\frac{\nu}{E}}(\sigma_{yy}+\sigma_{zz})\neq 0$
$\sigma_{xx}=0$でも$\varepsilon_{xx}\neq 0$なので注意。
$yz$平面の成分のみで整理すると以下のようになる。
$
\left(
\begin{array}{c}
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{yz}
\end{array}
\right)
=
{\displaystyle \frac{1}{E}}
\left[
\begin{array}{cccccc}
1& -\nu& 0\\
-\nu& 1& 0\\
0&0&1+\nu
\end{array}
\right]
\left(
\begin{array}{c}
\sigma_{yy}\\
\sigma_{zz}\\
\sigma_{yz}
\end{array}
\right)
$
$
\left(
\begin{array}{c}
\sigma_{yy}\\
\sigma_{zz}\\
\sigma_{yz}
\end{array}
\right)
=
{\displaystyle \frac{E}{1-\nu^{2}}}
\left[
\begin{array}{cccccc}
1& \nu& 0\\
\nu & 1& 0\\
0&0&1-\nu
\end{array}
\right]
\left(
\begin{array}{c}
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{yz}
\end{array}
\right)
$
${\displaystyle \frac{E}{1+\nu}=2G}$
金太郎飴のように$x$方向に同じ$yz$面が続き、$x$方向のひずみを無視できると
考える。
覚え方は「ひずみを無視したのが平面ひずみ」。
ただし、$x$方向の応力は無視できない。
応力―ひずみ関係の式に
$\varepsilon_{xx}=\varepsilon_{xy}=\varepsilon_{zx}=0$
を代入すると、以下のようになる。
$
\left(
\begin{array}{c}
\sigma_{xx}\\
\sigma_{yy}\\
\sigma_{zz}\\
\sigma_{yz}
\end{array}
\right)
=
{\displaystyle \frac{E}{(1+\nu)(1-2\nu)}}
\left[
\begin{array}{cccccc}
1-\nu & \nu & \nu & 0 \\
\nu & 1-\nu & \nu & 0 \\
\nu & \nu & 1-\nu & 0 \\
0 & 0 & 0 & 1-2\nu
\end{array}
\right]
\left(
\begin{array}{c}
0 \\
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{yz}
\end{array}
\right)
$
$\sigma_{xy}=0$
$\sigma_{zx}=0$
$\sigma_{xx}={\displaystyle \frac{\nu E}{(1+\nu)(1-2\nu)}(\varepsilon_{yy}
+\varepsilon_{zz})\neq 0}$
$\varepsilon_{xx}=0$でも$\sigma_{xx}\neq 0$なので注意。
$yz$平面の成分のみで整理すると以下のようになる。
$
\left(
\begin{array}{c}
\sigma_{yy}\\
\sigma_{zz}\\
\sigma_{yz}
\end{array}
\right)
=
{\displaystyle \frac{E}{(1+\nu)(1-2\nu)}}
\left[
\begin{array}{cccccc}
1-\nu & \nu & 0 \\
\nu & 1-\nu & 0 \\
0 & 0 & 1-2\nu
\end{array}
\right]
\left(
\begin{array}{c}
\varepsilon_{yy}\\
\varepsilon_{zz}\\
\varepsilon_{yz}
\end{array}
\right)
$
${\displaystyle \frac{E}{1+\nu}=2G}$
メモ:
