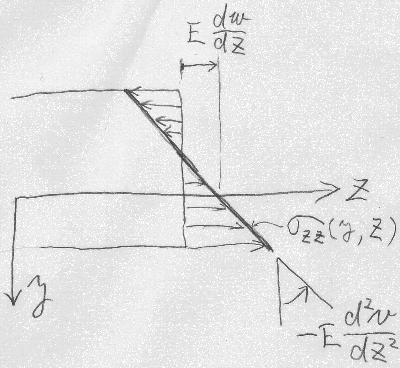
 軸方向の伸びひずみ$\varepsilon_{zz}$が桁高(けただか)$y$方向に
三角形分布しているのと同様に、
それを定数$E$倍した軸方向の直応力$\sigma_{zz}$も三角形分布している
ことになる。
軸方向の伸びひずみ$\varepsilon_{zz}$が桁高(けただか)$y$方向に
三角形分布しているのと同様に、
それを定数$E$倍した軸方向の直応力$\sigma_{zz}$も三角形分布している
ことになる。
注意: このページの数式は、 MathJaxを使って書いてます。 数式部分がおかしい場合は、更新ボタンをクリックすると 改善するかも知れません。 太文字のギリシャ文字($\mathbf{\sigma}$など)が、 太文字になっていない($\sigma$)かもしれません。 印刷版で確認して下さい。 その他、おかしい記述があると思ったら、 メールなどで指摘して下さい。
ひずみ-変位関係と
ベルヌーイ・オイラーの仮定から、
$yz$平面内で外力を受けて変形する
ベルヌーイ・オイラー梁の
ゼロでないひずみは、軸方向の伸びひずみだけで、
$\varepsilon_{zz}(y,z)=\frac{d w(z)}{dz}-y\frac{d^{2}v(z)}{dz^{2}}$
となることが導かれた。
1次元のフックの法則は、
$\sigma_{zz}=E\varepsilon_{zz}$
だから、これを上の$\varepsilon_{zz}$の式に代入すると、
$\sigma_{zz}(y,z)=E
(\frac{d w(z)}{dz}-y\frac{d^{2}v(z)}{dz^{2}})$
という直応力と図心変位の関係が導かれる。
 軸方向の伸びひずみ$\varepsilon_{zz}$が桁高(けただか)$y$方向に
三角形分布しているのと同様に、
それを定数$E$倍した軸方向の直応力$\sigma_{zz}$も三角形分布している
ことになる。
軸方向の伸びひずみ$\varepsilon_{zz}$が桁高(けただか)$y$方向に
三角形分布しているのと同様に、
それを定数$E$倍した軸方向の直応力$\sigma_{zz}$も三角形分布している
ことになる。
まずは基礎の章では、
外力を受けてつりあっている梁を適当な断面で切ったときに
その切断面に外力とつりあうように作用させる内力として、
梁の切断面の重心に作用する次の3つの力
軸力: 切断面に垂直な(軸方向の)1つの力
せん断力: 切断面に平行な1つの力
曲げモーメント: 切断面に作用する1つのモーメント
を断面力と、おおざっぱに定義したけど、
ほんとは初等梁の切断面には、
軸方向の直応力$\sigma_{zz}$が三角形分布しているから、
この直応力を断面に対して(積分して)合計したものが、
より正確な断面力の定義になりそうだ。
このように、断面力を
「断面に作用する応力を断面に対して積分して合計したもの」という
意味合いで、
合応力と呼ぶこともある。
合応力は応力ではなく断面力だから、
次元は「力」だったり「力×長さ」だったりする。
さて、土木や建築の分野では、
「応力」の意味で「応力度」という語を用い、
上記の「合応力」の意味で「応力」という語を用いるという
紛らわしい使い分けをする困った習慣が一部にある
(
例えば、平成14年度版の道路橋示方書でも「応力度」という表現が
使われ続けている
)。
「応力」を圧力の次元を持つ応力テンソル成分の意味で使うのが
物理の分野の一般的な使い方だと思うので、
このテキストでも「応力」は圧力の次元を持つ応力テンソル成分の意味で
用いることとし、「応力度」といった紛らわしい表現は使わない。
「ひずみ度」についてはひずみ-変位関係参照。
という訳で、まずは軸力を直応力$\sigma_{zz}$から求めてみたい。
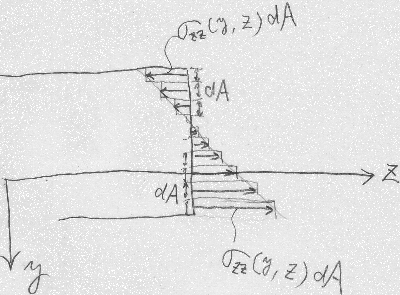 断面を面積$dA$の微小部分に分割して、
(この微小部分の範囲内では$\sigma_{zz}$が一様だとみなすなら)
それぞれの微小部分に$\sigma_{zz}(y,z)dA$の軸方向の力が作用していると
考えられる。
この軸方向の力$\sigma_{zz}(y,z)dA$をすべての微小部分に対して
合計すれば、断面の軸力が求まりそうだ。
微小部分を極限まで小さくしてやれば、これは面積積分で表せるから、
軸力$N$は、
断面を面積$dA$の微小部分に分割して、
(この微小部分の範囲内では$\sigma_{zz}$が一様だとみなすなら)
それぞれの微小部分に$\sigma_{zz}(y,z)dA$の軸方向の力が作用していると
考えられる。
この軸方向の力$\sigma_{zz}(y,z)dA$をすべての微小部分に対して
合計すれば、断面の軸力が求まりそうだ。
微小部分を極限まで小さくしてやれば、これは面積積分で表せるから、
軸力$N$は、
$N(z)=\int_{A}\sigma_{zz}(y,z)dA$
と定義できる。これに、
直応力-図心変位の関係を代入すると、
$N(z)=\int_{A}E
(\frac{d w(z)}{dz}-y\frac{d^{2}v(z)}{dz^{2}})dA$
$=E\int_{A}dA
\frac{d w(z)}{dz}
-
E\int_{A}ydA\frac{d^{2}v(z)}{dz^{2}}$
となる。
ここで
$\int_{A}dA$は
断面の微小部分の面積$dA$を全断面に対して合計したものだから全断面の
断面積そのもになるので、
断面積$A=\int_{A}dA$
とおく。
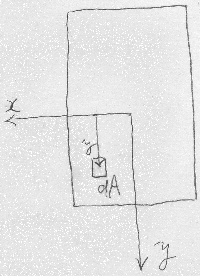 一方、$\int_{A}ydA$は、図のように、
断面の微小部分の面積$dA$と微小部分の$y$座標(正負の区別があるので注意)を
かけたものを全断面に対して積分して合計したものであり、
断面1次モーメントと呼ばれる定数(断面定数)である。
そこで、
一方、$\int_{A}ydA$は、図のように、
断面の微小部分の面積$dA$と微小部分の$y$座標(正負の区別があるので注意)を
かけたものを全断面に対して積分して合計したものであり、
断面1次モーメントと呼ばれる定数(断面定数)である。
そこで、
断面1次モーメント$J_{x}=\int_{A}ydA$
とおいて、軸力の式を書き直すと、
$N(z)=
EA\frac{d w(z)}{dz}
-
EJ_{x}\frac{d^{2}v(z)}{dz^{2}}$
となる。
$J_{x}$の添字$\ _{x}$は、$x$軸まわりの断面1次モーメントの意味で
つけている。
同様に$y$軸まわりの断面1次モーメント$J_{y}$は
$J_{y}=\int_{A}xdA$
と定義できる。
実は図心の座標$(x_{G}, y_{G})$は、
$y, x$軸まわりの
断面1次モーメント$J_{y}$, $J_{x}$を使って、
$x_{G}=\frac{J_{y}}{A}$
$y_{G}=\frac{J_{x}}{A}$
と定義できる。
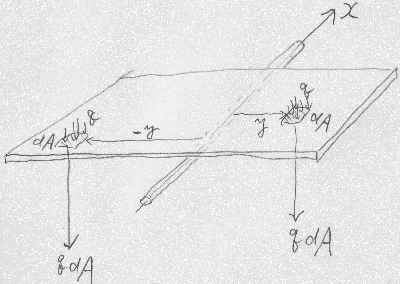 断面1次モーメントと図心のイメージは、こんなふうに
考えたらいいかも知れない。
$x$軸まわりの断面1次モーメント$J_{x}$の場合、
図のように、$x$軸が細い棒で、その上に梁断面の形をした板がのっていて、
板の単位面積あたりの重量が$q$の場合、
この板の$x$軸まわりのモーメントの合計を求めてみたい。
$x$軸よりも右側($y>0$)の微小部分$dA$は、
$x$軸右ねじまわりに$yqdA$のモーメントをつくるし、
$x$軸よりも左側($y<0$)の微小部分$dA$は、
$x$軸左ねじまわりに$-yqdA$のモーメントをつくるけど、
これを
$x$軸右ねじまわりになおすと結局$yqdA$だから、
この板の$x$軸まわりのモーメントの合計は、
$\int_{A}yqdA$となり、結局$qJ_{x}$となる。
つまり、$x$軸まわりの断面1次モーメント$J_{x}$は、
その断面の形の板を$x$軸(という水平の細い棒)にのせたときに、
$x$軸の右ねじまわりに
(単位面積あたり1の)自重でどれだけ回転しようとするかという
モーメントの合計を表していると言えるだろう。
つまり、$x$軸がちょうど図心上にあれば、
$x$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{x}$は0になる。
つまり水平な細長い棒の上に板を水平にして
板の図心をのせれば板は回転せずにつりあう
ことができる。
同様に、
$y$軸がちょうど図心上にあれば、
$y$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{y}$は0になる。
つまり、鉛直に立てた針の先に板を水平にして板の図心を
のせれば板は針の上でつりあっていることができる。
そのような針の先にのせたときにつりあう点のことを
我々は「重心」と呼んでいるが、単位面積あたりの重量が一様なら、
重心は図心と一致する。
さて、
ここで用いている初等梁のモデルでは、
$z$軸は図心を通っていることになっているので、
実は、断面1次モーメント$J_{x}$は0である。よって、
$z$軸上の任意点の
軸力$N(z)$は、結局
断面1次モーメントと図心のイメージは、こんなふうに
考えたらいいかも知れない。
$x$軸まわりの断面1次モーメント$J_{x}$の場合、
図のように、$x$軸が細い棒で、その上に梁断面の形をした板がのっていて、
板の単位面積あたりの重量が$q$の場合、
この板の$x$軸まわりのモーメントの合計を求めてみたい。
$x$軸よりも右側($y>0$)の微小部分$dA$は、
$x$軸右ねじまわりに$yqdA$のモーメントをつくるし、
$x$軸よりも左側($y<0$)の微小部分$dA$は、
$x$軸左ねじまわりに$-yqdA$のモーメントをつくるけど、
これを
$x$軸右ねじまわりになおすと結局$yqdA$だから、
この板の$x$軸まわりのモーメントの合計は、
$\int_{A}yqdA$となり、結局$qJ_{x}$となる。
つまり、$x$軸まわりの断面1次モーメント$J_{x}$は、
その断面の形の板を$x$軸(という水平の細い棒)にのせたときに、
$x$軸の右ねじまわりに
(単位面積あたり1の)自重でどれだけ回転しようとするかという
モーメントの合計を表していると言えるだろう。
つまり、$x$軸がちょうど図心上にあれば、
$x$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{x}$は0になる。
つまり水平な細長い棒の上に板を水平にして
板の図心をのせれば板は回転せずにつりあう
ことができる。
同様に、
$y$軸がちょうど図心上にあれば、
$y$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{y}$は0になる。
つまり、鉛直に立てた針の先に板を水平にして板の図心を
のせれば板は針の上でつりあっていることができる。
そのような針の先にのせたときにつりあう点のことを
我々は「重心」と呼んでいるが、単位面積あたりの重量が一様なら、
重心は図心と一致する。
さて、
ここで用いている初等梁のモデルでは、
$z$軸は図心を通っていることになっているので、
実は、断面1次モーメント$J_{x}$は0である。よって、
$z$軸上の任意点の
軸力$N(z)$は、結局
$N(z)=
EA\frac{d w(z)}{dz}
$
と表されることになる。
この$EA$は、伸び剛性と呼ばれ、
梁の伸び縮みしにくさを表している。
つまり応力が三角形分布している断面の直応力を、
断面形を考慮しながら積分して合計してやると、
ちょうど断面の図心での直応力$E\frac{dw(z)}{dz}$に断面積$A$
をかけたものと等しくなる。
一方、
図心から離れた位置の直応力に断面積をかけたものは、
直応力の合計とは、
ずれる。そのずれの大きさは、
三角形分布の傾きに断面1次モーメントとヤング率をかけたもの
($EJ_{x}\frac{d^{2}v(z)}{dz^{2}}$)となる。
 断面の直応力$\sigma_{zz}$から軸力を求めたのと同じ要領で、
次に
断面の曲げモーメントを直応力$\sigma_{zz}$から求めてみたい。
断面を面積$dA$の微小部分に分割して、
(この微小部分の範囲内では$\sigma_{zz}$が一様だとみなすなら)
それぞれの微小部分に$\sigma_{zz}(y,z)dA$の軸方向の力が作用していると
考えられる。
この軸方向の力$\sigma_{zz}(y,z)dA$に断面上の$y=0$の点まわりモーメントの腕の長さ
$y$をかけてすべての微小部分に対して
合計すれば、断面の曲げモーメントが求まりそうだ。
では。
微小部分を極限まで小さくしてやれば、これは面積積分で表せるから、
曲げモーメント$M$は、
断面の直応力$\sigma_{zz}$から軸力を求めたのと同じ要領で、
次に
断面の曲げモーメントを直応力$\sigma_{zz}$から求めてみたい。
断面を面積$dA$の微小部分に分割して、
(この微小部分の範囲内では$\sigma_{zz}$が一様だとみなすなら)
それぞれの微小部分に$\sigma_{zz}(y,z)dA$の軸方向の力が作用していると
考えられる。
この軸方向の力$\sigma_{zz}(y,z)dA$に断面上の$y=0$の点まわりモーメントの腕の長さ
$y$をかけてすべての微小部分に対して
合計すれば、断面の曲げモーメントが求まりそうだ。
では。
微小部分を極限まで小さくしてやれば、これは面積積分で表せるから、
曲げモーメント$M$は、
$M(z)=\int_{A}y\sigma_{zz}(y,z)dA$
と定義できる
(断面1次モーメントのところで説明したように、
$y>0$, $y<0$の部分で同じ向きの力がつくるモーメントの向きは逆まわりに
なるが、これは$y$の符号で表現されるのでそのまま$y$をかけて全領域に積分すれば
よい)。
これに、
直応力-図心変位の関係を代入すると、
$M(z)=\int_{A}yE
(\frac{d w(z)}{dz}-y\frac{d^{2}v(z)}{dz^{2}})dA$
$=E\int_{A}ydA
\frac{d w(z)}{dz}
-
E\int_{A}y^{2}dA\frac{d^{2}v(z)}{dz^{2}}$
となる。
ここで
$\int_{A}ydA$は軸力の節で説明したように
断面1次モーメント$J_{x}$と置き換えるとして、
今度は、$\int_{A}y^{2}dA$という積分が出てきた。
 $\int_{A}y^{2}dA$は、断面の
微小部分の面積$dA$と微小部分の$y$座標の2乗
(つまり$y$の正負は関係なくなる)をかけたものを
全断面に対して積分して合計したものであり、
断面2次モーメントと呼ばれる定数(断面定数)である。
そこで、
$\int_{A}y^{2}dA$は、断面の
微小部分の面積$dA$と微小部分の$y$座標の2乗
(つまり$y$の正負は関係なくなる)をかけたものを
全断面に対して積分して合計したものであり、
断面2次モーメントと呼ばれる定数(断面定数)である。
そこで、
断面2次モーメント$I=\int_{A}y^{2}dA$
とおいて、曲げモーメントの式を書き直すと、
$M(z)=
EJ_{x}
\frac{d w(z)}{dz}
-
EI\frac{d^{2}v(z)}{dz^{2}}$
となる。
断面1次モーメントのイメージの節で
説明したように、$x$軸が図心上にあれば断面1次モーメント$J_{x}$は0になるので、
$z$軸が図心を通っているこの初等梁のモデルでは、$J_{x}=0$となる。
よって、曲げモーメントは、結局
$M(z)=
-EI\frac{d^{2}v(z)}{dz^{2}}$
(重要)
と表されることになる。
この$EI$は
曲げ剛性と呼ばれ、
梁の曲がりにくさを表している。
なお、断面2次モーメント$I$が$x$軸まわりの断面2次モーメントであることを
強調する場合には、$I_{x}$と表記する。
さて、
曲げモーメント$M(z)$がたわみ$v(z)$の2階微分で表されているということは、
曲げモーメント分布が力のつりあいで求まる静定構造物なら、
これを$z$について2回積分すればたわみ$v(z)$を$z$の関数として求めることが
できそうである。
この方法については静定梁のたわみの章で述べる。
さて、
応力-図心変位関係
$\sigma_{zz}(y,z)=E
(\frac{d w(z)}{dz}-y\frac{d^{2}v(z)}{dz^{2}})$
に、
軸力-図心変位関係
$N(z)=EA\frac{d w(z)}{dz}$
と
曲げモーメント-たわみ関係
$M(z)=
-EI\frac{d^{2}v(z)}{dz^{2}}$
を代入すると、
$\sigma_{zz}(y,z)=
\frac{N(z)}{A}+\frac{M(z)}{I}y
$
という関係式が得られる。特に軸力$N$が作用していない場合には、
$\sigma_{zz}(y,z)=
\frac{M(z)}{I}y
$
(重要)
となる。これは、梁の断面力と断面形状が分かれば、
断面の直応力の三角形分布が求まる式なので重要であり、
公式として暗記しておく必要がある。
軸力$N$が作用していない場合、 曲げによる直応力の三角形分布は、図心(つまり$y=0$)でちょうど $\sigma_{zz}$が$0$になる。 このように$\sigma_{zz}$が(ということは$\varepsilon_{zz}$も)$0$に なっていて、 伸び縮みが発生していない面(この場合、$zx$平面)のことを 中立面と呼び、中立面が断面と交わる線を 中立軸と呼ぶ。 「伸び縮みが発生していない軸」として定義される中立軸は、 軸力が作用していない直線梁の場合は、図心を通る。
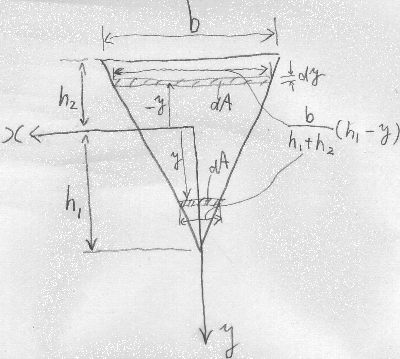 図のような二等辺三角形の対称軸に$y$軸を取り、
$x$軸を三角形の図心とは一致しない適当な位置に取った場合に、
この三角形の$x$軸回りの断面1次モーメントを求めてみたい。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
この微小部分の横幅は、
三角形の相似関係から$\frac{b}{h_{1}+h_{2}}(h_{1}-y)$となる
($y$は$x$軸より下か上かで正負の値を取るので、この式は
微小部分が$x$軸より下にあっても上にあっても成り立つ)。
微小部分の面積を$dA=\frac{b}{h_{1}+h_{2}}(h_{1}-y)dy$と置くと、
$x$軸まわりの断面1次モーメントは、
図のような二等辺三角形の対称軸に$y$軸を取り、
$x$軸を三角形の図心とは一致しない適当な位置に取った場合に、
この三角形の$x$軸回りの断面1次モーメントを求めてみたい。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
この微小部分の横幅は、
三角形の相似関係から$\frac{b}{h_{1}+h_{2}}(h_{1}-y)$となる
($y$は$x$軸より下か上かで正負の値を取るので、この式は
微小部分が$x$軸より下にあっても上にあっても成り立つ)。
微小部分の面積を$dA=\frac{b}{h_{1}+h_{2}}(h_{1}-y)dy$と置くと、
$x$軸まわりの断面1次モーメントは、
$J_{x}=\int_{A}ydA$
$=\int_{-h_{2}}^{h_{1}}y\frac{b}{h_{1}+h_{2}}(h_{1}-y)dy$
$=\int_{-h_{2}}^{h_{1}}\frac{b}{h_{1}+h_{2}}(h_{1}y-y^{2})dy$
$=\frac{b}{h_{1}+h_{2}}[\frac{h_{1}y^{2}}{2}-\frac{y^{3}}{3}]_{-h_{2}}^{h_{1}}$
$=\frac{b}{h_{1}+h_{2}}(
\frac{h_{1}^{3}}{2}-\frac{h_{1}^{3}}{3}-\frac{h_{1}h_{2}^{2}}{2}-\frac{h_{2}^{3}}{3}
)$
$=\frac{b}{6(h_{1}+h_{2})}(h_{1}^{3}-3h_{1}h_{2}^{2}-2h_{2}^{3})$
$=\frac{b}{6(h_{1}+h_{2})}
(h_{1}^{3}-h_{1}h_{2}^{2}-2h_{1}h_{2}^{2}-2h_{2}^{3})$
$=\frac{b}{6(h_{1}+h_{2})}
(h_{1}(h_{1}^{2}-h_{2}^{2})-2h_{2}^{2}(h_{1}+h_{2}))$
$=\frac{b}{6}(h_{1}(h_{1}-h_{2})-2h_{2}^{2})$
$=\frac{b}{6}(h_{1}^{2}-h_{1}h_{2}-h_{2}^{2}-h_{2}^{2})$
$=\frac{b}{6}((h_{1}+h_{2})(h_{1}-h_{2})
-h_{2}(h_{1}+h_{2}))$
$=\frac{b}{6}(h_{1}+h_{2})(h_{1}-2h_{2})$
となる。
さて、図心の$y$座標$y_{G}$を求めてみると、
$y_{G}=\frac{J_{x}}{A}$
$=\frac{\frac{b}{6}(h_{1}+h_{2})(h_{1}-2h_{2})}{\frac{b(h_{1}+h_{2})}{2}}$
$=\frac{h_{1}-2h_{2}}{3}$
となる。さて、原点がちょうど図心に来るようにするには、
$y_{G}=0$とおけばいいから、
$\frac{h_{1}-2h_{2}}{3}=0$から
$h_{1}=2h_{2}$となり、三角形の図心は頂点から
高さの$\frac{2}{3}$の位置にあることがわかる。
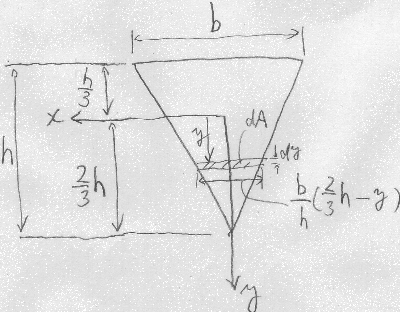 次に、$x$軸がこの三角形の図心上にある場合に、
この三角形の$x$軸まわりの断面2次モーメントを求めてみよう。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
この微小部分の横幅は、
三角形の相似関係から$\frac{b}{h}(\frac{2}{3}h-y)$となる
($y$は$x$軸より下か上かで正負の値を取るので、この式は
微小部分が$x$軸より下にあっても上にあっても成り立つ)。
微小部分の面積を$dA=\frac{b}{h}(\frac{2}{3}h-y)dy$と置くと、
$x$軸まわりの断面2次モーメントは、
次に、$x$軸がこの三角形の図心上にある場合に、
この三角形の$x$軸まわりの断面2次モーメントを求めてみよう。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
この微小部分の横幅は、
三角形の相似関係から$\frac{b}{h}(\frac{2}{3}h-y)$となる
($y$は$x$軸より下か上かで正負の値を取るので、この式は
微小部分が$x$軸より下にあっても上にあっても成り立つ)。
微小部分の面積を$dA=\frac{b}{h}(\frac{2}{3}h-y)dy$と置くと、
$x$軸まわりの断面2次モーメントは、
$I=\int_{A}y^{2}dA$
$=\int_{-\frac{h}{3}}^{\frac{2}{3}h}y^{2}\frac{b}{h}(\frac{2}{3}h-y)dy$
$=\frac{b}{h}\int_{-\frac{h}{3}}^{\frac{2}{3}h}
(\frac{2}{3}hy^{2}-y^{3})dy$
$=\frac{b}{h}[\frac{2}{3}h\frac{y^{3}}{3}-\frac{y^{4}}{4}]
_{-\frac{h}{3}}^{\frac{2}{3}h}$
$=\frac{b}{h}
(\frac{2^{4}h^{4}}{3^{5}}-\frac{2^{4}h^{4}}{4\cdot 3^{4}}
+\frac{2h^{4}}{3^{5}}+\frac{h^{4}}{4\cdot 3^{4}})$
$=\frac{bh^{3}}{3^{4}}
(\frac{16}{3}-4+\frac{2}{3}+\frac{1}{4})$
$=\frac{bh^{3}}{3^{4}}
(2+\frac{1}{4})$
$=\frac{bh^{3}}{36}$
となる。
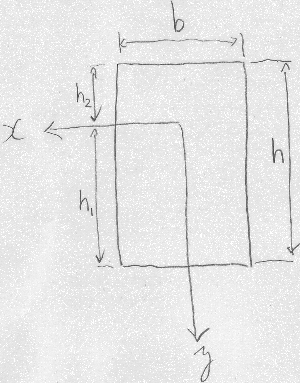 図のような長方形の$x$軸まわりの断面1次モーメントと図心の位置、
断面2次モーメントを求めよ。
また$x$軸が図心上にある場合、
長方形の
断面2次モーメントが$\frac{bh^{3}}{12}$となる
ことを示せ。
図のような長方形の$x$軸まわりの断面1次モーメントと図心の位置、
断面2次モーメントを求めよ。
また$x$軸が図心上にある場合、
長方形の
断面2次モーメントが$\frac{bh^{3}}{12}$となる
ことを示せ。
$J_{x}=\int_{A}ydA=\int_{-h_{2}}^{h_{1}}ybdy$
$=[b\frac{y^{2}}{2}]_{-h_{2}}^{h_{1}}
=\frac{b(h_{1}^{2}-h_{2}^{2})}{2}$
$I=\int_{A}y^{2}dA=\int_{-h_{2}}^{h_{1}}y^{2}bdy$
$=[b\frac{y^{3}}{3}]_{-h_{2}}^{h_{1}}
=\frac{b(h_{1}^{3}+h_{2}^{3})}{3}$
$y_{G}=\frac{J_{x}}{A}=\frac{h_{1}-h_{2}}{2}$
$y_{G}=0$とおくと、$h_{1}=h_{2}$なので、
$I=\frac{b(2h_{1}^{3})}{3}=\frac{bh^{3}}{12}$
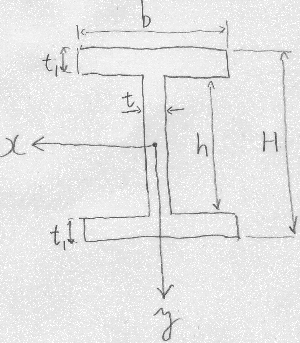 図のような2軸対称のI型断面の図心上に$x$軸があるとき、
$x$軸まわりの断面2次モーメントを求めよ。
図のような2軸対称のI型断面の図心上に$x$軸があるとき、
$x$軸まわりの断面2次モーメントを求めよ。
$I=\int_{A}y^{2}dA$
$=\int_{-\frac{H}{2}}^{-\frac{h}{2}}by^{2}dy
+\int_{-\frac{h}{2}}^{\frac{h}{2}}ty^{2}dy
+\int_{\frac{h}{2}}^{\frac{H}{2}}by^{2}dy$
$=[b\frac{y^{3}}{3}]_{-\frac{H}{2}}^{-\frac{h}{2}}
+[t\frac{y^{3}}{3}]_{-\frac{h}{2}}^{\frac{h}{2}}
+[b\frac{y^{3}}{3}]_{\frac{h}{2}}^{\frac{H}{2}}$
$=\frac{bH^{3}-(b-t)h^{3}}{12}$
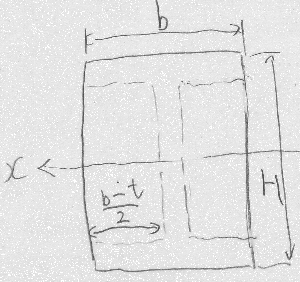 ついでに、$b \times h$の長方形に対する公式$\frac{bh^{3}}{12}$
を利用するなら、$b \times H$の大きい長方形の断面2次モーメントから
$\frac{b-t}{2}\times h$の小さい長方形2個ぶんの断面2次モーメントを
引くという便法によって求めた答えが、面積積分による答えと
一致することを確認せよ。
ついでに、$b \times h$の長方形に対する公式$\frac{bh^{3}}{12}$
を利用するなら、$b \times H$の大きい長方形の断面2次モーメントから
$\frac{b-t}{2}\times h$の小さい長方形2個ぶんの断面2次モーメントを
引くという便法によって求めた答えが、面積積分による答えと
一致することを確認せよ。
メモ: