
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
第3回で、
梁モデルでゼロにならない唯一のひずみは、
軸方向の直ひずみだけで、
$\varepsilon_{zz}(y,z)=w'(z)-yv''(z)$
となることが導かれた。
1次元のフックの法則は、
$\sigma_{zz}=E\varepsilon_{zz}$
だから、これに上の$\varepsilon_{zz}$の式を代入すると、
$\sigma_{zz}(y,z)=Ew'(z)-yEv''(z)$
という直応力と図心変位の関係が導かれる。
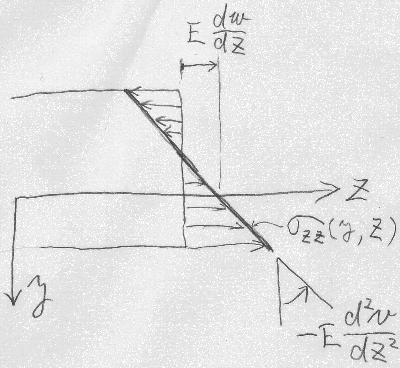 軸方向の伸びひずみ$\varepsilon_{zz}$が桁高(けただか)$y$方向に
三角形分布していたのと同様に、
それを定数$E$倍した軸方向の直応力$\sigma_{zz}$も三角形分布している
ことになる。
ある断面$z=z_{A}$で考えれば、
$z$切片が$Ew'(z_{A})$で、傾きが$-Ev''(z_{A})$だ。
軸方向の伸びひずみ$\varepsilon_{zz}$が桁高(けただか)$y$方向に
三角形分布していたのと同様に、
それを定数$E$倍した軸方向の直応力$\sigma_{zz}$も三角形分布している
ことになる。
ある断面$z=z_{A}$で考えれば、
$z$切片が$Ew'(z_{A})$で、傾きが$-Ev''(z_{A})$だ。
つまり、梁モデルの断面には、このように直応力が三角形分布しているのが、
より正確な梁の内力の状態ということになるが、
これを構造力学I第5回でやった
軸力$N$: 切断面に垂直な(軸方向の)1つの力
せん断力$S$: 切断面に平行な1つの力
曲げモーメント$M$: 切断面に作用する1つのモーメント
にまとめて表すにはどうしたらいいだろうか。
構造力学I第1回でやったように、
複数の作用点に作用している複数の力であれば、
それらを鉛直成分、水平成分に分解して、
それぞれ合計してやればいいし、モーメントだったら、
腕の長さをかけながら合計してやればよかった。
では、応力のように面に連続的に作用している力の場合は、
どうやって合計したらいいだろうか。
連続的に変化する量を合計する方法は「積分」である。
積分も色々あるが、断面に分布している応力を積分して合計したいから、
この場合は、面積積分(面積分)を使う。
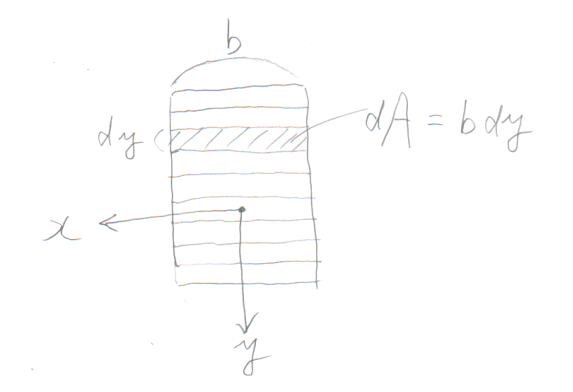 というわけで、まずはある断面の軸力$N$を、
その断面に分布する直応力$\sigma_{zz}$を面積積分して合計することで
求めてみたい。
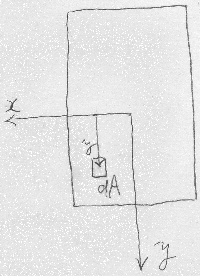
断面を簡単のため長方形断面ということにして、
図のように細いしましまの微小部分に分割する。
$yz$平面の$z$軸に横たわる梁の断面は$xy$平面になる。
この微小部分の面積$dA$は、高さ$dy$で幅$b$なので、
$dA=bdy$となる。
こういう微小部分を表すときにつける$d$は「微小な」という
意味である。
微分や積分で出てくる$dx$とかの$d$も基本的にそういう意味である。
微小な部分を有限個で見えるように描いて、それらを足し算すると
とらえれば、積分をイメージしやすい。
この微小部分を0まで小さくして無限個に増やせば積分ということになる。
というわけで、まずはある断面の軸力$N$を、
その断面に分布する直応力$\sigma_{zz}$を面積積分して合計することで
求めてみたい。
断面を簡単のため長方形断面ということにして、
図のように細いしましまの微小部分に分割する。
$yz$平面の$z$軸に横たわる梁の断面は$xy$平面になる。
この微小部分の面積$dA$は、高さ$dy$で幅$b$なので、
$dA=bdy$となる。
こういう微小部分を表すときにつける$d$は「微小な」という
意味である。
微分や積分で出てくる$dx$とかの$d$も基本的にそういう意味である。
微小な部分を有限個で見えるように描いて、それらを足し算すると
とらえれば、積分をイメージしやすい。
この微小部分を0まで小さくして無限個に増やせば積分ということになる。
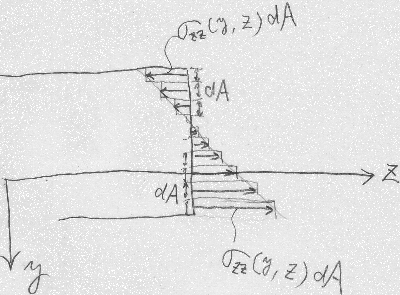 応力の三角形分布を、この微小部分の中では平均化してしまい、
1つの微小部分の中は一様な応力が作用していることにすると、
図のように、階段状に応力が分布していることになる。
実際には、微小部分の高さ$dy$の中でも応力は三角形分布しているのだが、
その高さの中央の値で代表させたと考えてもいいだろう。
図では、微小部分の高さが$dA$であるかのように書いているが、
これは、あくまで高さ$dy$に幅$b$をかけた微小面積$dA$を
$yz$平面上で表しているためにこう書いている。
こういう書き方が気持ち悪いと思う人は、
ひとまず、幅$b$が1だと考えてもよい。
応力の三角形分布を、この微小部分の中では平均化してしまい、
1つの微小部分の中は一様な応力が作用していることにすると、
図のように、階段状に応力が分布していることになる。
実際には、微小部分の高さ$dy$の中でも応力は三角形分布しているのだが、
その高さの中央の値で代表させたと考えてもいいだろう。
図では、微小部分の高さが$dA$であるかのように書いているが、
これは、あくまで高さ$dy$に幅$b$をかけた微小面積$dA$を
$yz$平面上で表しているためにこう書いている。
こういう書き方が気持ち悪いと思う人は、
ひとまず、幅$b$が1だと考えてもよい。
すると、それぞれの微小部分には、
その高さ$y$における直応力$\sigma_{zz}(y,z)$が分布している。
これを力の次元にするには、この高さ$y$の直応力に、
微小部分の面積$dA$をかけてやればよいから、
それぞれの微小部分には、$\sigma_{zz}(y,z)dA$の力が軸方向に作用していると
考えられる。
この軸方向の力$\sigma_{zz}(y,z)dA$をすべての微小部分に対して
合計すれば、断面の軸力が求まりそうだ。
微小部分を極限まで小さくしてやれば、これは面積積分で表せるから、
軸力$N$は、
${\displaystyle N(z)=\int_{A}\sigma_{zz}(y,z)dA}$
と定義できる。
$\sigma_{zz}$は引張が正で圧縮が負だから、
どこからどこまでが引張でどこからどこまでが圧縮なんてことは
気にせずに上から下まで積分(合計)すれば、
ちゃんと圧縮成分は引き算される。
これに、上の
直応力-図心変位の関係
$\sigma_{zz}(y,z)=Ew'(z)-yEv''(z)$
を代入すると、
${\displaystyle
N(z)=E\int_{A}dA
w'(z)
-
E\int_{A}ydAv''(z)}$
となる。
$xy$面の面積積分の場合は、$dA$は$x$と$y$に関係するため、$dx$や$dy$で
表され、$x$や$y$で積分することになるが、
$z$には関係しない。
だから、$w'(z)$や$v''(z)$は積分の外に出すことができる。
ある断面$z=z_{A}$について考えている場合、これらは定数となる。
ここで
${\displaystyle \int_{A}dA}$は
断面の微小部分の面積$dA$を全断面に対して合計したものだから全断面の
断面積そのもになるので、
断面積${\displaystyle A=\int_{A}dA}$
とおく。
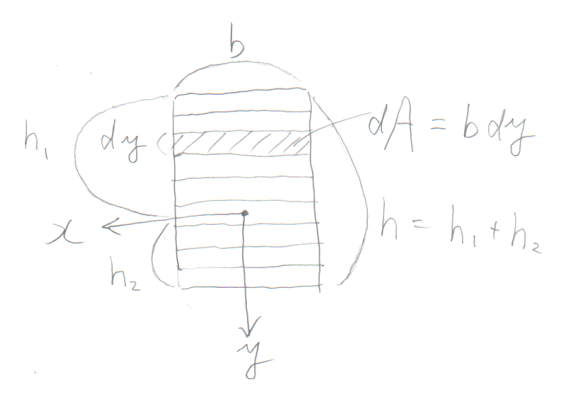 面積積分は数学の授業のどれかでやっているのではないかとは思うが、
例えば、図のような幅$b$, 高さ$h$の長方形断面で微小部分$dA$を合計するなら、
$dA=bdy$と表せるから、以下のように$y$についての積分で計算できる。
面積積分は数学の授業のどれかでやっているのではないかとは思うが、
例えば、図のような幅$b$, 高さ$h$の長方形断面で微小部分$dA$を合計するなら、
$dA=bdy$と表せるから、以下のように$y$についての積分で計算できる。
${\displaystyle A=\int_{A}dA=\int_{-h_{1}}^{h_{2}}bdy}
$
$=\Bigl[by\Bigr]_{-h_{1}}^{h_{2}}
$
$=b(h_{2}+h_{1})=bh$
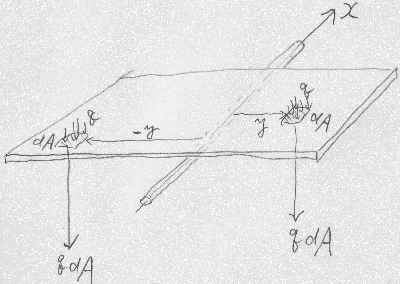
 一方、${\displaystyle \int_{A}ydA}$は、図のように、
断面の微小部分の面積$dA$と微小部分の$y$座標を
かけたものを全断面に対して積分して合計したものであり、
断面1次モーメントと呼ばれる定数(断面定数)である。
微小部分は、(応力が$x$方向にも変化する場合など)一般的には
図のように$x$方向にも微小な幅で与えるが、それはともかく、
この微小部分の座標$y$は、ひとまず、微小部分の中央の座標と捉えておいて
いいだろう。
断面1次モーメントの詳しい説明は次項でするとして、
ひとまず、
一方、${\displaystyle \int_{A}ydA}$は、図のように、
断面の微小部分の面積$dA$と微小部分の$y$座標を
かけたものを全断面に対して積分して合計したものであり、
断面1次モーメントと呼ばれる定数(断面定数)である。
微小部分は、(応力が$x$方向にも変化する場合など)一般的には
図のように$x$方向にも微小な幅で与えるが、それはともかく、
この微小部分の座標$y$は、ひとまず、微小部分の中央の座標と捉えておいて
いいだろう。
断面1次モーメントの詳しい説明は次項でするとして、
ひとまず、
断面1次モーメント${\displaystyle J_{x}=\int_{A}ydA}$
(重要)
とおいて、軸力の式を書き直すと、
$N(z)=
EAw'(z)
-
EJ_{x}v''(z)$
となる。
これで、軸力$N(z)$については、図心変位(の微分)と関係づけることができた。
$J_{x}$の添字$\ _{x}$は、$x$軸まわりの断面1次モーメントの意味で
つけている。
同様に$y$軸まわりの断面1次モーメント$J_{y}$は
${\displaystyle J_{y}=\int_{A}xdA}$
と定義できる。
実は図心の座標$(x_{G}, y_{G})$は、
$y, x$軸まわりの
断面1次モーメント$J_{y}$, $J_{x}$を使って、
${\displaystyle x_{G}=\frac{J_{y}}{A}}\\$
${\displaystyle y_{G}=\frac{J_{x}}{A}}$
と定義できる。なぜそうなるかについては、
次回触れる。
さて、
断面1次モーメント${\displaystyle J_{x}=\int_{A}ydA}$
の積分を実行すると、$y$(長さ)に$dA$(面積)をかけることになるから、
断面1次モーメント$J_{x}$の次元は、$(長さ)^{3}$になる。
単位としては、m$^{3}$とかmm$^{3}$とかになるが、
物理的意味は次項に説明するように$x$軸回りのモーメントであり、
別に「体積」のことではないので、
読み方は「立方メートル」よりは「(ミリ)メートルの3乗」とかでいいと思う。
下に出てくる断面2次モーメントの単位は$(長さ)^{4}$になるので、
「(ミリ)メートルの4乗」だし、
3次元の薄肉ばりで出てくる「そりねじり定数」だと「(ミリ)メートルの6乗」だ。
人によって読み方は違うし、あまり本質的なことではない。
脱線:小学校では、
cm$^{2}$のような面積の単位を「平方センチメートル」と教え、
これが、cmの2乗であることを教えない。
しかも、cmのcが、$\frac{1}{100}$という意味で、
cmは、$\frac{1}{100}\times$mの意味だということも教えない。
だから、横2cm, 縦3cmの長方形の面積は、
2cm$\times$3cm=6(cm)$^{2}$のようにcmを2回かけているから、
cm$^{2}$なのだということも教えてもらえない。
つまり、小学生は、単位というのは、「長さ」とか「時間」といった
基本的な次元を表す単位をかけたり割ったりした結果として、
計算すれば自動的に求まるということも知らない。
なんとも、もったいない話だと思う。
まあ、面積については、累乗を習う前なので、
「センチメートルの2乗」というのを教えられないということもあるのかもしれないが、
それだったら、面積や体積の単位を教える前に、
$3^{2}=9$みたいなのをちょっと教えておけば済む話だと思う。
2cmと3cmをかけたから、6(cm)$^2$になったと理解できるメリットの方が
はるかに大きいと思う。
だから、私は面積や体積の単位も、
「メートルの2乗」とか「メートルの3乗」とか、式をそのまま読んだ方が、
小学生や中学生の理解を助けると考えている。
速さは、小学校では「毎秒10メートル」とか「時速60km」といった
表現を使うと思うし、これは日常の表現でもあるが、
単位として書く場合は、
10m/秒(または 10$\frac{\text{m}}{秒}$)とか
60km/時(または60km/時間 または
60$\frac{\text{km}}{時間}$)を使ってほしい。
そして、読み方は、
「メートル毎秒」とか「キロメートル毎時」とかではなく、
「メートルわる秒」とか「キロメートルわる時間」と
式をそのまま読んでもいいことにしてほしい。
式をそのまま読んだ方が意味がわかるし、
距離を時間で割ると速さになるとか、
速さに時間をかけると距離になるという意味を式として理解できる。
小学校や中学校では、単位のある量の計算をする際に、
数値だけで計算させるが、ぜひ、単位も一緒に計算させるべきだと
私は考えている。
時速60kmの車で10分走ったら、何メートル走れますかみたいな問題は、
単位をそろえてから数値だけを計算させるのが小学校の流儀だけど、
以下のように、まずは単位を含めて式を書いてしまってから、
それを眺めて、約分できるように1つずつ単位をそろえればいいのではないだろうか。
60km/時$\times$10分
$=60\times\frac{\text{km}}{時間}\times 10分
=60\times\frac{1000 \text{m}}{60分}\times 10分
=\not{60}\times\frac{1000 \text{m}}{\not{60}\not{分}}\times 10\not{分}
=10000\text{m}
$
単位も一緒に計算した結果、単位が求める答え(距離)の単位に
ならなければ、計算に間違いがあることに気づくこともできるが、
数値だけ計算していたのでは、こうした次元の間違いに気づくことができない。
単位を式の通りに読ませるとか、
単位を一緒に計算させるといった工夫をすることで、
物理量の次元を意識する習慣が身につくような気がする。
一方で、
はじきみたいなパターンマッチングに頼って、次元を意識せずに数値だけ計算させるような
やり方は、小学生を思考停止に誘導しているのではないかと私は思う。
 断面1次モーメントと図心のイメージは、こんなふうに
考えたらいいかも知れない。
$x$軸まわりの断面1次モーメント$J_{x}$の場合、
図のように、$x$軸が細い棒で、その上に梁断面の形をした板がのっていて、
板の単位面積あたりの重量が$q$の場合、
この板の$x$軸まわりのモーメントの合計を求めてみたい。
$x$軸よりも右側($y>0$)の微小部分$dA$は、
下向きに$qdA$で引っ張られて、モーメントの腕の長さ(絶対値)は$y$だから
$x$軸右ねじまわりに$yqdA$のモーメントをつくるし、
$x$軸よりも左側($y<0$)の微小部分$dA$は、
下向きに$qdA$で引っ張られて、モーメントの腕の長さ(絶対値)は$-y$だから
$x$軸左ねじまわりに$-yqdA$のモーメントをつくるけど、
これを
$x$軸右ねじまわりになおすとどちらも$yqdA$になるから、
この板の$x$軸まわりのモーメントの合計は、
${\displaystyle \int_{A}yqdA}$でいいことになり、結局$qJ_{x}$となる。
つまり、$x$軸まわりの断面1次モーメント$J_{x}$は、
その断面の形の板を$x$軸(という水平の細い棒)にのせたときに、
$x$軸の右ねじまわりに
(単位面積あたり1の)自重でどれだけ回転しようとするかという
モーメントの合計を表していると言えるだろう。
つまり、$x$軸がちょうど図心上にあれば、
$x$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{x}$は0になる。
つまり水平な細長い棒の上に板を水平にして
板の図心をのせれば板は回転せずにつりあう
ことができる。
同様に、
$y$軸がちょうど図心上にあれば、
$y$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{y}$は0になる。
つまり、鉛直に立てた針の先に板を水平にして板の図心を
のせれば板は針の上でつりあっていることができる。
そのような針の先にのせたときにつりあう点のことを
我々は「重心」と呼んでいるが、単位面積あたりの重量が一様なら、
重心は図心と一致する。
さて、
ここで用いている梁のモデルでは、
$z$軸は図心を通っていることになっているので、
実は、断面1次モーメント$J_{x}$は0である。
断面1次モーメントと図心のイメージは、こんなふうに
考えたらいいかも知れない。
$x$軸まわりの断面1次モーメント$J_{x}$の場合、
図のように、$x$軸が細い棒で、その上に梁断面の形をした板がのっていて、
板の単位面積あたりの重量が$q$の場合、
この板の$x$軸まわりのモーメントの合計を求めてみたい。
$x$軸よりも右側($y>0$)の微小部分$dA$は、
下向きに$qdA$で引っ張られて、モーメントの腕の長さ(絶対値)は$y$だから
$x$軸右ねじまわりに$yqdA$のモーメントをつくるし、
$x$軸よりも左側($y<0$)の微小部分$dA$は、
下向きに$qdA$で引っ張られて、モーメントの腕の長さ(絶対値)は$-y$だから
$x$軸左ねじまわりに$-yqdA$のモーメントをつくるけど、
これを
$x$軸右ねじまわりになおすとどちらも$yqdA$になるから、
この板の$x$軸まわりのモーメントの合計は、
${\displaystyle \int_{A}yqdA}$でいいことになり、結局$qJ_{x}$となる。
つまり、$x$軸まわりの断面1次モーメント$J_{x}$は、
その断面の形の板を$x$軸(という水平の細い棒)にのせたときに、
$x$軸の右ねじまわりに
(単位面積あたり1の)自重でどれだけ回転しようとするかという
モーメントの合計を表していると言えるだろう。
つまり、$x$軸がちょうど図心上にあれば、
$x$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{x}$は0になる。
つまり水平な細長い棒の上に板を水平にして
板の図心をのせれば板は回転せずにつりあう
ことができる。
同様に、
$y$軸がちょうど図心上にあれば、
$y$軸まわりのモーメントがつりあうので、
断面1次モーメント$J_{y}$は0になる。
つまり、鉛直に立てた針の先に板を水平にして板の図心を
のせれば板は針の上でつりあっていることができる。
そのような針の先にのせたときにつりあう点のことを
我々は「重心」と呼んでいるが、単位面積あたりの重量が一様なら、
重心は図心と一致する。
さて、
ここで用いている梁のモデルでは、
$z$軸は図心を通っていることになっているので、
実は、断面1次モーメント$J_{x}$は0である。
よって、
$z$軸上の任意点の
軸力$N(z)$は、結局
$N(z)=
EAw'(z)
$
と表されることになる。
この$EA$は伸び剛性と呼ばれ、
梁の伸び縮みしにくさを表している。
$w'(z)$は、第2回でやったように、
図心位置での直ひずみ
$\varepsilon_{zz}(z)=w'(z)$であるから、
$N(z)=EA\varepsilon_{zz}(y=0,z)$とも書ける。
1次元のフックの法則から、$\sigma_{zz}=E\varepsilon_{zz}$であるから、
これは、
$N(z)=A\sigma_{zz}(y=0,z)$ということになり、
つまり、図心位置の直応力に断面積をかけたものが軸力ということである。
 上で、
断面の直応力$\sigma_{zz}$から軸力を求めたのと同じ要領で、
次に
断面の曲げモーメントを直応力$\sigma_{zz}$から求めてみたい。
断面を面積$dA$の微小部分に分割して、
(この微小部分の範囲内では$\sigma_{zz}$が一様だとみなすなら)
それぞれの微小部分に$\sigma_{zz}(y,z)dA$の軸方向の力が作用していると
考えられる。
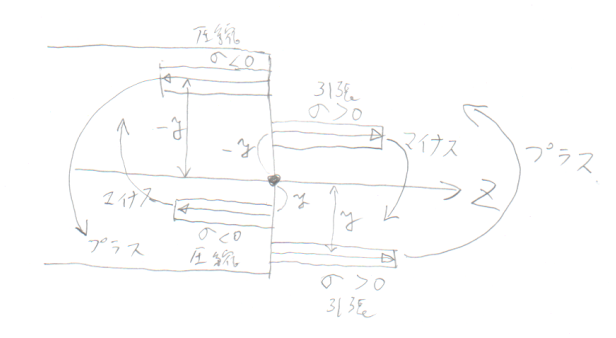
曲げモーメントの中心は、断面の$x$軸($yz$平面で見るなら、断面と$z$軸の交点)
としよう。
そうすると、モーメントの腕の長さは、
$z$軸より上の$y<0$のところでは$-y$で、
$z$軸より下の$y<0$のところでは$y$で表せる。
曲げモーメントの正の向きは、
構造力学I第5回でやったように、
下側引張が正で、
図の断面では反時計回りになるから、
モーメントの中心(断面と$z$軸の交点)まわりに、
反時計回りのモーメントをつくる力はプラスで、
時計回りのモーメントをつくる力はマイナスで、
足していけばよい。
細かいことが気になる人のために、ちゃんと
場合分けしておく。気にならない人は飛ばしてもよい。
上で、
断面の直応力$\sigma_{zz}$から軸力を求めたのと同じ要領で、
次に
断面の曲げモーメントを直応力$\sigma_{zz}$から求めてみたい。
断面を面積$dA$の微小部分に分割して、
(この微小部分の範囲内では$\sigma_{zz}$が一様だとみなすなら)
それぞれの微小部分に$\sigma_{zz}(y,z)dA$の軸方向の力が作用していると
考えられる。
曲げモーメントの中心は、断面の$x$軸($yz$平面で見るなら、断面と$z$軸の交点)
としよう。
そうすると、モーメントの腕の長さは、
$z$軸より上の$y<0$のところでは$-y$で、
$z$軸より下の$y<0$のところでは$y$で表せる。
曲げモーメントの正の向きは、
構造力学I第5回でやったように、
下側引張が正で、
図の断面では反時計回りになるから、
モーメントの中心(断面と$z$軸の交点)まわりに、
反時計回りのモーメントをつくる力はプラスで、
時計回りのモーメントをつくる力はマイナスで、
足していけばよい。
細かいことが気になる人のために、ちゃんと
場合分けしておく。気にならない人は飛ばしてもよい。
というわけで結局、モーメントの合計は、
軸方向の力$\sigma_{zz}(y,z)dA$(引張のときは正、圧縮のときは負)に
微小部分の座標$y$($z$軸より下だと正、上だと負)をかけた
$y\sigma_{zz}(y,z)dA$を、すべての場合についてそのまま足していけば、
ちゃんと断面の図心の反時計回りのモーメントが求まる。
この
微小部分を極限まで小さくしてやれば、これは面積積分で表せるから、
曲げモーメント$M$は、
${\displaystyle M(z)=\int_{A}y\sigma_{zz}(y,z)dA}$
と定義できる。
ちなみに、この断面と向き合う方の断面で考えると、
正の曲げモーメントの向きは時計回りになるから、
時計回りのモーメントを合計することになるが、
その場合も
同じ式で表せるので、気になる人は自分で考えてほしい。
これに、
直応力-図心変位の関係
$\sigma_{zz}(y,z)=Ew'(z)-yEv''(z)$
を代入すると、
${\displaystyle M(z)=\int_{A}yE}$
${\displaystyle =E\int_{A}ydA
w'(z)
-
E\int_{A}y^{2}dAv''(z)}$
となる。
ここで
${\displaystyle \int_{A}ydA}$は軸力のところで説明したように
断面1次モーメント$J_{x}$と置き換えるとして、
今度は、${\displaystyle \int_{A}y^{2}dA}$という積分が出てきた。
 ${\displaystyle \int_{A}y^{2}dA}$は、断面の
微小部分の面積$dA$と微小部分の$y$座標の2乗
(つまり$y$の正負は関係なくなる)をかけたものを
全断面に対して積分して合計したものであり、
断面2次モーメントと呼ばれる定数(断面定数)である。
$y^{2}$に面積$dA$をかけているから、この積分を実行すると、
次元は$(長さ)^{4}$となり、単位はm$^{4}$とかmm$^{4}$とかである。
読みは「メートルの4乗」とか「ミリメートルの4乗」とか、好きなように。
さて、
${\displaystyle \int_{A}y^{2}dA}$は、断面の
微小部分の面積$dA$と微小部分の$y$座標の2乗
(つまり$y$の正負は関係なくなる)をかけたものを
全断面に対して積分して合計したものであり、
断面2次モーメントと呼ばれる定数(断面定数)である。
$y^{2}$に面積$dA$をかけているから、この積分を実行すると、
次元は$(長さ)^{4}$となり、単位はm$^{4}$とかmm$^{4}$とかである。
読みは「メートルの4乗」とか「ミリメートルの4乗」とか、好きなように。
さて、
断面2次モーメント${\displaystyle I=\int_{A}y^{2}dA}$
(重要)
とおいて、曲げモーメントの式を書き直すと、
$M(z)=
EJ_{x}
w'(z)
-
EIv''(z)$
となる。
断面1次モーメントのイメージのところで
説明したように、$x$軸が図心上にあれば断面1次モーメント$J_{x}$は0になるので、
$z$軸が図心を通っているこの梁モデルでは、$J_{x}=0$となる。
よって、曲げモーメントは、結局
$M(z)=
-EIv''(z)$
(重要)
と表されることになる。
この$EI$は
曲げ剛性と呼ばれ、
梁の曲がりにくさを表している。
なお、断面2次モーメント$I$が$x$軸まわりの断面2次モーメントであることを
強調する場合には、$I_{x}$と表記する。
さて、
曲げモーメント$M(z)$がたわみ$v(z)$の2階微分で表されているということは、
曲げモーメント$M(z)$が力のつりあいで求まる静定構造物なら、
これを$z$について2回積分すればたわみ$v(z)$を$z$の関数として求めることが
できそうである。
この方法については
第7回で教えるので、楽しみにしておいてほしい。
さて、
応力-図心変位関係
$\sigma_{zz}(y,z)=Ew'(z)-yEv''(z)$
に、
軸力-軸方向変位関係
$N(z)=
EAw'(z)
$
と
曲げモーメント-たわみ関係
$M(z)=
-EIv''(z)$
を代入すると、
${\displaystyle \sigma_{zz}(y,z)=
\frac{N(z)}{A}+\frac{M(z)}{I}y
}$
という関係式が得られる。特に軸力$N$が作用していない場合には、
${\displaystyle \sigma_{zz}(y,z)=
\frac{M(z)}{I}y}
$
(重要)
となる。これは、梁の断面力と断面形状が分かれば、
断面の直応力の三角形分布が求まる式なので重要であり、
公式として暗記しておく必要がある。
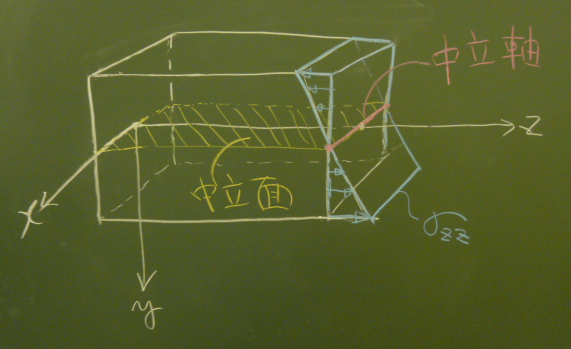 軸力$N$が作用していない場合、
曲げによる直応力の三角形分布は、図心(つまり$y=0$)でちょうど
$\sigma_{zz}$が$0$になる。
このように$\sigma_{zz}$が(ということは$\varepsilon_{zz}$も)$0$に
なっていて、
伸び縮みが発生していない面(この場合、$zx$平面)のことを
中立面と呼び、中立面が断面と交わる線を
中立軸と呼ぶ。
「伸び縮みが発生していない軸」として定義される中立軸は、
軸力が作用していない直線梁の場合は、図心を通る。
軸力$N$が作用していない場合、
曲げによる直応力の三角形分布は、図心(つまり$y=0$)でちょうど
$\sigma_{zz}$が$0$になる。
このように$\sigma_{zz}$が(ということは$\varepsilon_{zz}$も)$0$に
なっていて、
伸び縮みが発生していない面(この場合、$zx$平面)のことを
中立面と呼び、中立面が断面と交わる線を
中立軸と呼ぶ。
「伸び縮みが発生していない軸」として定義される中立軸は、
軸力が作用していない直線梁の場合は、図心を通る。
軸力が作用している場合の中立軸の定義には、ゆれがあるかもしれない。
「伸び縮みが発生していない軸」(つまり、軸方向直ひずみ$\varepsilon_{zz}(y,z)=0$)の軸ではなく、
$\varepsilon_{zz}(y,z)=\varepsilon_{zz}^{のび}(y,z)+\varepsilon_{zz}^{曲げ}(y,z)$
のように軸方向直ひずみをのび成分と曲げ成分に分解した場合の
曲げ成分$\varepsilon_{zz}^{曲げ}(y,z)=0$の軸を中立軸とする流儀も
あるかもしれない。
さて、今回は、梁の断面に作用している直応力$\sigma_{zz}$を面積積分することで、 軸力$N(z)$や曲げモーメント$M(z)$を応力から求めることができた。 あれ? そういえば、せん断力$S(z)$は、どうなっているんだろう? 初等梁モデルでは、 第2回の梁モデルの仮定でやったように、 平面保持の仮定と断面形不変の仮定から軸方向の直ひずみ$\varepsilon_{zz}$以外の ひずみはすべて0になり、 だから第2回の応力-ひずみ関係(せん断) でやったように、 せん断応力はせん断ひずみに比例するから、すべて0になり、 1次元のフックの法則が成り立つような細長い棒では、 $\sigma_{xx}=\sigma_{yy}=0$とみなせて、 結局、初等梁のモデルで、0でない応力は、 $\sigma_{zz}$のみということになる。 断面に分布している $\sigma_{zz}$を合計すれば軸力になったり、 図心からの腕の長さをかけながら合計すれば曲げモーメントになったり、 というのは理解できるが、 $z$軸方向に分布している $\sigma_{zz}$を、どう合計したって、 断面に平行に作用するせん断力$S(z)$は出てこない。 せん断力$S(z)$は、 第4回で、 断面に一様にせん断応力$\sigma_{yz}$が作用している場合は、 $\sigma_{yz}=\frac{S}{A}$と表されることから考えれば、 断面に一様でないせん断応力が分布している場合は、 $S(z)=\int_{A}\sigma_{yz}dA$みたいに、 せん断応力を面積積分して求めるべきではないだろうか。 ところが、 初等梁モデルでは、せん断応力$\sigma_{yz}$はゼロなので、 せん断力$S$はないことになってしまう。 なんか、おかしい。 実は、初等梁理論というのは、ちょっと強引な仮定を設けているために、 そういうおかしい点も含んでいる。 そうすると、構造力学Iでは、あることになっている せん断力$S(z)$をどう与えればいいのかということになるが、 これについては第9回辺りでやるので、 楽しみにしておいてほしい。
梁モデルの軸方向の直ひずみと直応力、
断面の軸力と曲げモーメントは、
次式のように与えられることがわかった。
$\varepsilon_{zz}(y,z)=w'(z)-yv''(z)$
$\sigma_{zz}(y,z)=Ew'(z)-yEv''(z)$
$N(z)=EAw'(z)$
$M(z)=-EIv''(z)$
さて、$\sigma_{zz}(y,z)$
を$N(z)$と$M(z)$を用いて表わせ。
答えはここ。
 梁の断面に$\varepsilon_{zz}(z)=w'(z)$で表される
一様な直ひずみが発生している。
梁の断面に$\varepsilon_{zz}(z)=w'(z)$で表される
一様な直ひずみが発生している。
1次元のフックの法則$\sigma_{zz}(z)=E\varepsilon_{zz}\varepsilon_{zz}(z)$が
成立つとき、$\sigma_{zz}(z)$を断面について面積積分して、
断面の軸力$N(z)$を求めよ。
ただし、断面積は$A$とする。
答えは、ここ。
 図のように、梁の断面に$\sigma_{zz}(y,z)=-Eyv''(z)$で表される
直応力が作用している。
$E$はヤング率、$v(z)$はたわみである。
このとき、$\sigma_{zz}$を面積積分して、
断面の曲げモーメント$M(z)$を求めよ。
ただし、${\displaystyle I=\int_{A}y^{2}dA}$とおく。
また、$\sigma_{zz}$を$M(z)$を用いて表わせ。
答えはここ。
図のように、梁の断面に$\sigma_{zz}(y,z)=-Eyv''(z)$で表される
直応力が作用している。
$E$はヤング率、$v(z)$はたわみである。
このとき、$\sigma_{zz}$を面積積分して、
断面の曲げモーメント$M(z)$を求めよ。
ただし、${\displaystyle I=\int_{A}y^{2}dA}$とおく。
また、$\sigma_{zz}$を$M(z)$を用いて表わせ。
答えはここ。
 図のような梁のたわみ$v(z)$が、
$v(z)=\frac{P}{6EI}(3\ell z^{2}-z^{3})$で表されるとき、
曲げモーメント$M(z)$を求めよ。
答えはここ。
図のような梁のたわみ$v(z)$が、
$v(z)=\frac{P}{6EI}(3\ell z^{2}-z^{3})$で表されるとき、
曲げモーメント$M(z)$を求めよ。
答えはここ。
2022年度小テスト:
小テスト221109
2021年度小テスト:
問,
解答
2020年度小テスト:
問1,
解答
メモ: