
注意: 以下の手引きは2023年度用に書いたものを、2024年度用に書き換えている途中である。
以下のレポート提出方法などに関する手引きは、 後藤・青木担当の「構造実験」についてしか当てはまらないので、 他の実験(コンクリ、水理、土質)に関しては、それぞれの 担当教員の指示に従うこと。
この実験の趣旨について、 事前にある程度 把握しておくためには、以下の動画を見ておくとよい。 2022年度版動画その1、 2022年度版動画その2、 2022年度版動画その3 (参考:古いやつ)。
土木環境工学実験は、受講者50人を4〜5人ずつの10の班(A〜J)に分け、 コンクリ実験4回、構造実験2回、 水理実験2回、土質実験3回の、計11回を 下記の表のようなローテーションで 行います。
2024年度の構造実験は
引張試験と
曲げ試験
の2回ぶんで、
座屈試験は行いません。
以下の説明をよく読み、
データ処理し、グラフを描き、
それらをワープロに貼り付けるなどして作成して下さい。
提出形式はpdfにして下さい。
pdfファイルにエクスポートするには、
例えば
ワードの場合は「Adobe PDFとして保存」を選択して下さい。
ただし、pdfファイルはワードで編集はできないので、
編集用にワードファイルも保存しておく必要はあります。
レポートの提出は、
構造の2回目の実験を行った翌週(1週間後)の
木曜日の12:00までに2回ぶんの実験についてまとめて
WebClassから
提出するものとします(後述)。
構造実験では、
引張試験で算出した材料定数を用いて、
曲げ試験のたわみ
を予測したり、引張試験から算出される材料定数と
曲げ試験から算出される材料定数を比較したりする必要があるので、
2回の実験を両方とも行ってから、まとめて考察してもらうことにします。
| 5/9 | 5/16 | 5/23 | 5/30 | 6/13 | 6/20 | 6/27 | 7/4 | 7/11 | 7/18 | 7/25 | 8/1 | |
| A班 | 構1 | 構2 | ||||||||||
| B班 | 構2 | 構1 | ||||||||||
| C班 | 構1 | 構2 | ||||||||||
| D班 | 構2 | 構1 | ||||||||||
| E班 | 構1 | 構2 | ||||||||||
| F班 | 構2 | 構1 | ||||||||||
| G班 | 構1 | 構2 | ||||||||||
| H班 | 構2 | 構1 | ||||||||||
| I班 | 構1 | 構2 | ||||||||||
| J班 | 構2 | 構1 |
構造実験は、 後述 する ように 実験装置自体は小規模な実験なので、 作業服などを着てくる必要はありませんが (勿論、作業服が一番でしょうが)、 一応、実験に適したかっこうをして下さい。 具体的には、
といったことです。
服装のせいで、
あと、
実験に参加する前に必ず、その
実験の解説
(
引張試験、
曲げ試験
)をよく読み、
どのような実験をどのような手順で行うのかを予習して把握しておくこと
(予習してこないと、それだけ説明に時間がかかって実験が長引いたり、
班の他の人に迷惑をかけたりします)。
実験にはノートと筆記用具と電卓(関数電卓があるなら、その方が望ましいが)を
持ってくること。
あと、データを電子ファイルで受け取れるように
USBフラッシュメモリを(複数の人が)持ってきてほしい。
レポートの書き方は、以下を読めば十分ではあるが、 動画も見たい人は、 2022年度版動画 その1、 その2、 その3 (参考:古いやつ)を見て下さい (2022年度は WebClassから pdfファイルをアップロードして提出してもらうので、 提出期限とか紙の綴じ方とかは、無視してほしい)。
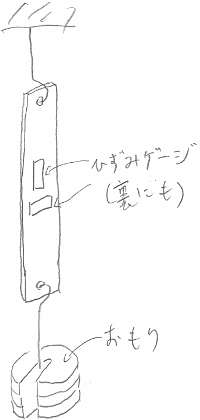 縦横に張った ひずみゲージにより、
軸方向と軸直角方向の ひずみを求める。
軸方向応力は、載荷した荷重を試験片の断面積で割れば求まるから、
応力-ひずみ曲線
(を最小二乗法で線形回帰した回帰直線)
の傾きとしてヤング率を求める。
縦横に張った ひずみゲージにより、
軸方向と軸直角方向の ひずみを求める。
軸方向応力は、載荷した荷重を試験片の断面積で割れば求まるから、
応力-ひずみ曲線
(を最小二乗法で線形回帰した回帰直線)
の傾きとしてヤング率を求める。
軸方向ひずみと軸直角方向ひずみとの比からポアソン比を求める。 (アクリル材は、たぶん等方性材料なので) ヤング率とポアソン比からせん断弾性係数を求める。
薄い板を1軸方向に引っ張った場合の応力とひずみの関係については、 構造力学のウェブテキスト参照 (数式の表示にはFirefoxが必要だけど、情報処理センターの 端末のFirefoxでも見れる)。
実験では、線形的に分布する (x,y) 座標値のデータから、
x と y の関係を最小二乗法で線形回帰するということが多々ある。
線形回帰をやってくれる各種ツールは色々とあるが、
(一生のうちに)
一度ぐらいは手を動かして(って言っても電卓ぐらいは使っていいけど)
計算してみるのも悪くないと思う。
プログラムを組みたい人は、
この辺も参考まで。
エクセルを使って線形回帰のグラフを描きたいなら、
例えば「エクセル 線形回帰」といったキーワードで
ウェブ検索してみよう。
Windows 版の
フリーソフトで回帰直線を描いてくれるツールとしては、
エクセルと同じように表計算ソフトとして操作したいんだったら、
LibreOfficeとか
(これは、Linux版やMacOS X版もある)。
操作のしやすさ(データからグラフの描きやすさ)という意味では、
Ngraph
とか。
操作しにくいけど強力な上級者?向けツールは、
gnuplot
とか
(Windows版もある。参考まで)。
アクリルの試験体は、写真のように脚立にぶら下げてある。
ひずみゲージは、丸い2軸のものが貼ってあるが、
縦ひずみ測定用の縦のゲージと横ひずみ測定用の横のゲージが
1枚の中に一緒になっているものを使った。
これが、裏面にも貼ってある。
ひずみゲージに触らないようにして、試験体の幅を3箇所、ノギスで測定する。
以下は、オンライン授業の場合のデータ例。
| 1班 | 1箇所目 | 2箇所目 | 3箇所目 |
| 幅(mm) | 18.96 | 18.99 | 19.14 |
| 厚さ(mm) | 5.01 | 5.09 | 5.06 |
| 2班 | 1箇所目 | 2箇所目 | 3箇所目 |
| 幅(mm) | 18.86 | 19.39 | 19.04 |
| 厚さ(mm) | 5.09 | 5.18 | 5.01 |
| 3班 | 1箇所目 | 2箇所目 | 3箇所目 |
| 幅(mm) | 19.34 | 18.88 | 19.04 |
| 厚さ(mm) | 5.01 | 5.00 | 5.01 |
| 4班 | 1箇所目 | 2箇所目 | 3箇所目 |
| 幅(mm) | 19.05 | 19.03 | 19.02 |
| 厚さ(mm) | 5.01 | 5.07 | 5.03 |
| 5班 | 1箇所目 | 2箇所目 | 3箇所目 |
| 幅(mm) | 19.01 | 18.97 | 19.02 |
| 厚さ(mm) | 5.01 | 5.11 | 5.02 |
ひずみゲージに触らないようにして、試験体の厚さを3箇所、ノギスで測定する。
試験体に重りフックの引っかかった状態で、
ひずみ測定器を初期化し、この状態を荷重0とする。
測定を開始し、
ストップウォッチで、
30秒経過ごとに1kgfの重りを1つ載せ、
揺れを抑えて、30秒経過後(測定開始から60秒後)に次の重りを載せ、...
という具合に、17個×1kgf=合計17kgfの重りを30秒+30秒×17回=540秒間に
載荷していく。
540秒経過すると、ひずみ測定は自動で終了する。

自分の班のデータ(1回目、2回目)をダウンロードすること。 コンマ区切りで書かれた CSV形式なので、 エクセルやLibreOfficeなどの表計算ツールに読み込んで加工することができる。 実験日の室温については、 自分の班の 曲げ試験データに書かれた室温を参照すること。
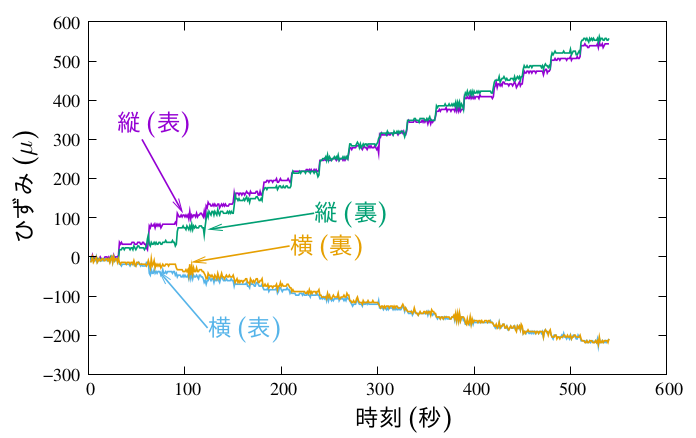 上記のデータは、ひずみを測定した生データが、
1列目:時刻(秒),
2列目:縦ひずみ表(μ),
3列目:縦ひずみ裏(μ),
4列目:横ひずみ表(μ),
5列目:横ひずみ裏(μ)
の順に並んでいる。
これをそのままプロットすると、図のように、
30秒ごとに階段状にひずみが増えていく(横ひずみは圧縮なのでマイナス)
グラフになる。
これから、応力-ひずみのグラフをつくるためには、
まず、重りなしの状態から、
30秒間ずつ18段階で17個の重りを載せた、それぞれの段階に
対応するひずみと応力を求める必要がある。
応力に関しては、重り1個が1kgfだから、
0kgfから17kgfまでを
N(ニュートン)に換算してから、
測定した断面積で割り算すれば、18段階に対応する応力が求まるだろう。
ひずみに関しては、1段階につき30秒間に30個のデータがあるので、
これからどのように代表値を求めれかいいかを考えなければならない。
こちらから、こうしなさいとは言わないので、
各自の考えでデータを整理してほしい。
あまり深く考えずに、30秒間の真ん中辺りの15秒の時のひずみデータを
採用するという考えもあるだろう。しかし、
グラフを見ると、30秒間の間にもギザギザと値が上下に揺れているのがわかる。
そうすると、15秒のときのデータが、たまたま上に振れていたり、
たまたま下に振れていたりするだろうから、このやり方では、ばらつきが
大きくなりそうだ。
では、ばらつきをならすために、30秒間のデータを平均してしまうという
考えもあるだろう。
でも、重りを載せる瞬間は、30秒間経過時ちょうどにうまく静かに
載せられるとは限らないから、
重りを載せる瞬間の前後は、あまり信用できるデータではないかもしれない。
上記のデータは、ひずみを測定した生データが、
1列目:時刻(秒),
2列目:縦ひずみ表(μ),
3列目:縦ひずみ裏(μ),
4列目:横ひずみ表(μ),
5列目:横ひずみ裏(μ)
の順に並んでいる。
これをそのままプロットすると、図のように、
30秒ごとに階段状にひずみが増えていく(横ひずみは圧縮なのでマイナス)
グラフになる。
これから、応力-ひずみのグラフをつくるためには、
まず、重りなしの状態から、
30秒間ずつ18段階で17個の重りを載せた、それぞれの段階に
対応するひずみと応力を求める必要がある。
応力に関しては、重り1個が1kgfだから、
0kgfから17kgfまでを
N(ニュートン)に換算してから、
測定した断面積で割り算すれば、18段階に対応する応力が求まるだろう。
ひずみに関しては、1段階につき30秒間に30個のデータがあるので、
これからどのように代表値を求めれかいいかを考えなければならない。
こちらから、こうしなさいとは言わないので、
各自の考えでデータを整理してほしい。
あまり深く考えずに、30秒間の真ん中辺りの15秒の時のひずみデータを
採用するという考えもあるだろう。しかし、
グラフを見ると、30秒間の間にもギザギザと値が上下に揺れているのがわかる。
そうすると、15秒のときのデータが、たまたま上に振れていたり、
たまたま下に振れていたりするだろうから、このやり方では、ばらつきが
大きくなりそうだ。
では、ばらつきをならすために、30秒間のデータを平均してしまうという
考えもあるだろう。
でも、重りを載せる瞬間は、30秒間経過時ちょうどにうまく静かに
載せられるとは限らないから、
重りを載せる瞬間の前後は、あまり信用できるデータではないかもしれない。
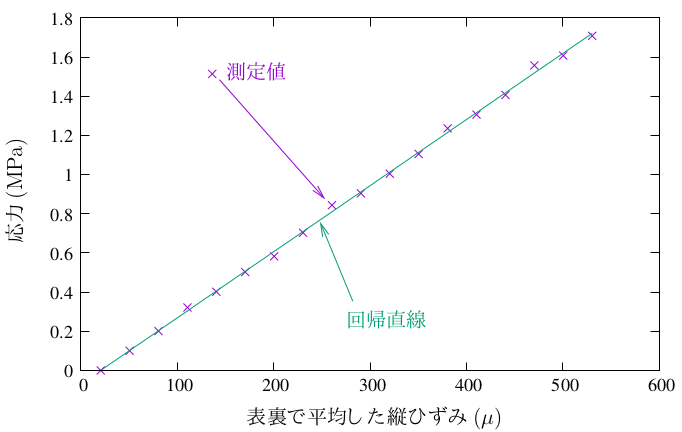 そうすると、例えば、
ある程度 揺れがおさまった16秒辺りから、次の重りが載る影響のない
25秒辺りの10個のデータで平均するといった考えもある。
生データをエクセルやLibreOffice等の
表計算ツールで開いて、手動でそのように平均を求めていっても
大した手間ではないだろう。
プログラムを組める人は、
生データを読み込んで、そのように処理したデータを吐くプログラムを
組むのもいいだろう(例えばgfortranの例:s-e.f90)。
表計算ツールの処理もプログラムを組むのも苦手だけど、
まあまあのデータを取りたいという人は、
せめて揺れが落ち着いて、次の載荷の影響の少ない25秒のデータだけを拾ってみるというやり方もあるかも知れない。
裏と表のデータの扱いをどうするかについても様々な選択肢がある。
裏と表で、かなり傾向が異なる場合は、裏と表を平均したりせずに、
ばらばらに考察すべきかもしれない。
このようにデータ処理の方法は、様々なやり方があり得るので、
どのような考えに基づいて、どのようにデータ処理したのか、
自分の「意見」の部分をちゃんと書くこと。
そうすると、例えば、
ある程度 揺れがおさまった16秒辺りから、次の重りが載る影響のない
25秒辺りの10個のデータで平均するといった考えもある。
生データをエクセルやLibreOffice等の
表計算ツールで開いて、手動でそのように平均を求めていっても
大した手間ではないだろう。
プログラムを組める人は、
生データを読み込んで、そのように処理したデータを吐くプログラムを
組むのもいいだろう(例えばgfortranの例:s-e.f90)。
表計算ツールの処理もプログラムを組むのも苦手だけど、
まあまあのデータを取りたいという人は、
せめて揺れが落ち着いて、次の載荷の影響の少ない25秒のデータだけを拾ってみるというやり方もあるかも知れない。
裏と表のデータの扱いをどうするかについても様々な選択肢がある。
裏と表で、かなり傾向が異なる場合は、裏と表を平均したりせずに、
ばらばらに考察すべきかもしれない。
このようにデータ処理の方法は、様々なやり方があり得るので、
どのような考えに基づいて、どのようにデータ処理したのか、
自分の「意見」の部分をちゃんと書くこと。
以下は古い資料
以下はだいぶ古くなりましたが、 LibreOfficeでもOpenOfficeと大体 同じように操作できるのではないかと思います。 エクセルの線形回帰のやり方も検索すればいっぱいヒットするでしょう。
まず、情報処理センターの端末で、起動時に2を選んで、 SUSE Linuxを起動してログインする。 画面の適当なところで右クリックして「端末を開く」を選び、 コマンドを打ち込めるターミナルを開いておく。 左下の「コンピュータ」のとこをクリックすると出てくる Firefoxを起動して、このページ (http://www.str.ce.akita-u.ac.jp/~gotou/zikken/) を表示させておく。 グラフにしたい横軸データが1列目、縦軸データが2列目に半角スペースを はさんで並んでいるテキストファイル(例えばsin.txt)を 作る。実験の生データのコンマ区切り csv形式ファイルをもとにテキストエディターで 編集してもいいだろうし、表計算ソフトからテキスト形式で保存してもいいだろう。 表計算ソフトから保存する場合は、テキスト形式(csv形式となってるかも)で 保存することと区切り文字をスペース区切りにすることをお忘れなく。 情報処理センターのSUSE Linuxで作業する場合は、 フラッシュメモリからファイルを読み込んで作業すればよい。 テキストエディターを使う場合は、 ターミナルでgedit&と打ち込むとエディターが立ち上がるし、 表計算ソフトを使う場合は左下の「コンピュータ」ボタンからOpenOfficeを起動すればよい。 次に、この oresen.txt のファイルを sin.txtが置いてあるディレクトリに保存する。 ターミナルでgedit oresen.txt&としてテキストエディターで oresen.txtを開き、 横軸ラベル、縦軸ラベル、入力ファイル名(ここではsin.txt)、 出力ファイル名(拡張子は.pngにすること)を編集する。 ラベルは半角英数文字でないと表示できないので、 tawami(mm) みたいにローマ字で書いて構わない (日本語や全角文字を使わないように)。 そして、ターミナルでgnuplot<oresen.txtと打ち込んでエンターキーを押す。 すると、出力ファイル名に指定した画像ファイル(この例ではsin.png)が 出力されている。 出力された画像ファイルを表示して確認するには、ターミナルで eog sin.png&のように(eog の後に画像ファイル名を)打ち込む。 SUSE Linux上のOpenOfficeでレポートを作成するなら、 この画像ファイルを「挿入」→「画像」→「ファイルから」で選択して 貼りつければいいし、Windows上のワードなどでレポートを書きたいなら、 画像ファイルをフラッシュメモリなどにコピーして持ち出せばよい。
情報処理センターの端末で Linuxを選択して起動した場合、 フラッシュメモリやデジカメなどの外部メディアをUSB端子で接続すると、 自動的に認識されて、デスクトップ上に外部メディアのアイコンが現れると思う。 画像ファイルなどのコピー作業などが終わってUSB端子を抜く場合は、 まず、この外部メディアのアイコン上で右クリックして、 「アンマウント」を選択し、外部メディアのアイコンが消えてから抜き取ること。 もし、「アンマウント」という選択肢がなくて「ボリュームのマウント」みたいな 選択肢しかなかったら、まず「ボリュームのマウント」を選択してから 右クリックすると、アンマウントが現れる。
上の 情報処理センターのgnuplotでグラフを描く方法 の要領で、 情報処理センター端末のSUSE Linuxにログインし、 Firefoxを立ち上げてこのページを表示する。それから Gnome端末を立ち上げてコマンドを打ち込めるようにしておく。 グラフにしたい横軸データが1列目に、 縦軸データが2列目に半角スペースをはさんでならんでいるテキストファイル (例えばhippari.txt)を作る (作り方は上参照)。 次にこのkaiki.txtのファイルを hippari.txtが置いてあるディレクトリに 保存する。 ターミナルでgedit kaiki.txt&としてテキストエディターで kaiki.txtを開き、 横軸ラベル、縦軸ラベル、入力ファイル名(ここではhippari.txt)、 出力ファイル名(拡張子は.pngにすること)を編集する。 ラベルは半角英数文字でないと表示できないので、 tawami(mm) みたいにローマ字で書いて構わない (日本語や全角文字を使わないように)。 あと横軸、縦軸の単位を自分の設定した単位にするように (MPaみたいな補助単位k,M,Gなどを使って構わないし、 *10-6を*10^{-6}とか適当に工夫して書いて構わない)。 ターミナルで、 gnuplot<kaiki.txtと打ち込んでエンターキーを押す。 すると、 ターミナル画面に Final set of parameters として、 y=ax+bに線形回帰した係数aとbが表示され、 出力ファイル名に指定した画像ファイル(この例ではhippari.png)が 出力されている。 出力された画像ファイルを表示して確認するには、ターミナルで eog hippari.png&のように(eog の後に画像ファイル名を)打ち込む。 SUSE Linux上のOpenOfficeでレポートを作成するなら、 この画像ファイルを「挿入」→「画像」→「ファイルから」で選択して 貼りつければいいし、Windows上のワードなどでレポートを書きたいなら、 画像ファイルをフラッシュメモリなど (抜くときの注意)にコピーして持ち出せばよい。
ひずみ測定器の設定は、こちらで準備しておくが、一応、 ゲージ率の設定についてメモしておく。 ひずみゲージは、変形とともに長さが変わって抵抗値が変わることにより ひずみを測定するセンサーである。 今、長さLで、抵抗値Rの抵抗線がΔLだけ伸びて、 抵抗値がΔRだけ変化したとすると、 ひずみεの定義は、ε=ΔL/Lですが、このとき、 ΔR/R=Kε という関係が成り立つ。 K はゲージ率(ゲージファクター、感度係数)で、2.0前後が標準とされている。 で、一般的なひずみ測定器(ロガー)の初期設定では、 ゲージ率を 2.0 とした値、つまりΔR/(2.0*R) が出力されるようになっている (ΔR/R が出力される訳ではないので注意)。 さて、ゲージ率が 2.15 のひずみゲージを使う場合は、 出力表示に掛ける補正係数をいくらにすればよいかというと、 2.0/2.15≒0.930 にすれば、 0.930*ΔR/(2.0*R)≒ΔR/(2.15*R) となっって、ゲージ率 2.15 の値に 補正されることになる (間違って補正係数を 1/2.15 にしてしまうと、 結果の値が半分になってしまうという失敗を私はやらかしました。すいません)。
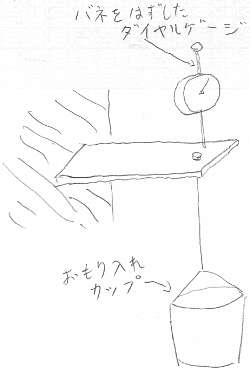 アクリル片持ち梁の自由端の荷重とたわみの関係を測定し、それを
片持ち梁の先端のたわみの式
(まあ、みなさん公式みたいに覚えてますよね)に
代入してヤング率を求める。
そうすると、引張試験から求めた
ヤング率とは、それなりに喰い違う値が算定されるのではないかと
思うんだけど、
それが単なる誤差のせいなのか、
理論的にも喰い違ってていいのか、
その辺を考察してもらう。
アクリル片持ち梁の自由端の荷重とたわみの関係を測定し、それを
片持ち梁の先端のたわみの式
(まあ、みなさん公式みたいに覚えてますよね)に
代入してヤング率を求める。
そうすると、引張試験から求めた
ヤング率とは、それなりに喰い違う値が算定されるのではないかと
思うんだけど、
それが単なる誤差のせいなのか、
理論的にも喰い違ってていいのか、
その辺を考察してもらう。
曲げ試験体の幅をノギスで3箇所 測定する。
曲げ試験体の厚さをノギスで3箇所 測定する。
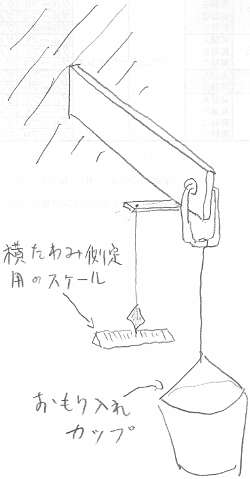
曲げ試験体を写真のように、万力と鋼板を使って
片持ち梁状態で固定し、固定端部(アクリルを固定した鋼板のヘリ)から、
重り載荷用のフックの位置までをノギスを使って3回測定する。
測定したら、変位計を重り載荷位置のできるだけ近傍に、
複数の方向から眺めて鉛直になるように設置し
(梁がたわんでも変位計の針が梁から離れないように、数cm押し付けた状態で)、
変位計の目盛りを初期化しておく。
1個40gfの重りをカップに静に入れ、
変位計の数値の振れがある程度 おさまったら、変位を記録する。
次に2つめの重りをカップに入れ、
変位計の数値の振れがある程度 おさまったら、変位を記録する。
これを重り14個(計560gf)まで繰り返す。
すべての重りをカップに入れて変位を測定したら、
カップから重りをすべて取り、
10分程度、試験体を休ませてから、
変位計を設置し直し、再び同じことをする。

試験体の幅、厚さ、曲げ試験時のたわみ変位のデータを以下からダウンロードすること。 拡張子.odsのファイルはLibreOffice用、拡張子.xlsxのファイルはエクセル用だが、 たぶん、 どっちでどっちを開いても読み込めると思う。
 引張試験をまだ行っていない場合は、
座屈試験が終わった後に引張試験も行うこと。
引張試験をまだ行っていない場合は、
座屈試験が終わった後に引張試験も行うこと。
図のような、片持ち梁の先端に、鉛直下向きに重りを載荷していくと、 最初のうちは、梁は面内で (片持ち梁の先端のたわみの式の通りに) たわんでいくけど、 徐々に (初期不整のない理想的な問題なら、ある臨界荷重に達した途端に)、 横方向へねじれながらたわみ始める。 これは、横ねじれ座屈とか横倒れ座屈と言われる座屈現象である。

Southwell法による座屈荷重の算定については、
「Southwell法について」を参照のこと。
*
Trahair, N. S.: Flexural-Torsional buckling of structures,
E & FN Spon, Chapman and Hall, London, England.
1993.
Timoshenko, S. P. and Gere, J. M.: Theory of elastc stability,
McGraw-Hill Book Company, Inc., 1961.
Chajes, A.:
Principles of structural stability theory,
Prentice-Hall, Inc. , Englewood Cliffs, N. J. , 1974.
長方形断面の ねじり定数 J, そりねじり定数 Iω を より厳密に
求めてみたい人は、
この辺参照。
長方形断面の断面二次モーメントは計算できないとダメですよ。
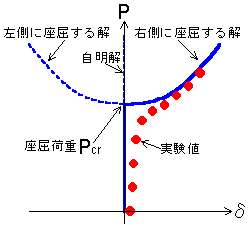
縦軸に荷重 P をとり、横軸に横たわみ δをとり、 荷重と横たわみの関係をプロットしてみると、 もし、まったく初期不整のない完全系の梁に(偏心などもなく) 理想的に載荷できたとすると、(現実には起きないけど) 図の青い線のように最初は 横たわみを生じずに (載荷面内だけにたわみながら) まっすぐ上がっていき、 ある荷重(座屈荷重)に達した途端に、急激に (右側か左側の面外に)横たわみを発生する(解が存在する)。 この他に、座屈点を超えても横たわみを生じずに、そのまま載荷面内に たわみ続けるという解も存在する。 これは分かってもしょうがない当たり前の解なので「自明解」とか trivial solutionと言う (意訳するなら「トリビアな解」?)。 この面外にたわまない自明解は、エネルギー的に不安定であるが、 自然界はエネルギー的に安定な解を選ぶので、 現実には面外にたわみが生じる解が選ばれる (という解説がよくなされる)。 しかし、実際の梁には様々な初期不整があるし、 載荷も理想的な条件でなされる訳ではないので、 実験値をプロットすると、図の赤い点のように、 最初から横たわみは少しずつ増えていくが、 座屈点に近づくにつれてその増え方が激しくなる。 でも、こういう実験値のプロットから座屈荷重を推定するのは なかなか難しい。
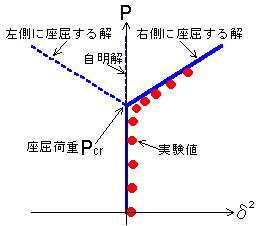
さて、座屈後の荷重-たわみ曲線を眺めてみると、 なんか、P=aδ2+Pcr みたいな式で近似できそうだ。 δ2じゃなくて、 δ4とかじゃだめなの? という指摘はなかなか鋭い。が、ここでは触れない。 という訳で、ためしに、横軸をδ2にして 荷重-たわみ曲線を書き直してみる。そうすると、 「完全系」の非自明解(自明でない方の解)は、 Pcrを切片とする直線になる。 ということは、座屈荷重の赤い点を P-δ2で プロットして、プロットが直線上に並んだところで回帰直線を引けば、 それが縦軸と交わった点を座屈荷重と推定できるという推定方法が、 有名な?「P-δ2法」である。 図を見ても分かる通り、「P-δ2法」は、 座屈後のたわみの大きい領域までプロットがないと正確な回帰直線が引けない。 しかし、弾性域で試験体を使いまわす座屈実験などでは、 試験体が塑性化しない範囲までしか載荷できないので、 なかなか座屈後のじゅうぶんなプロットは得られない。 そのような場合に適しているのが、Southwell法に よる算定方法である。
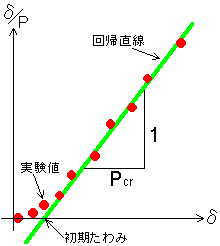
Southwell法*というのは、 縦軸に δ/P をとり、横軸に δ をとってプロットすると、 (なぜか)実験値が線形分布し、その回帰直線の傾きの逆数が 座屈荷重になるという推定方法である。 なぜそうなるかということを、 柱の座屈を例に簡略化した説明を 「Southwell法による座屈荷重の算定について」 (pdfファイル)に書いたので参照すること。 ちなみに、Meck法**というのは、 荷重-横たわみ関係に対して Southwellプロットを適用して求めた座屈荷重と、 荷重-ねじれ角関係に対して Southwellプロットを適用して求めた座屈荷重との 相乗平均を座屈荷重とする算定方法である(今回は ねじれ角を測定してないから 使えないけど)。
* Southwell, R. V.: On the Analysis of Experimental Observations in Problems
of Elastic Stability, Proc. Royal Soc. London (A), 135, 601-616, 1932.
** Meck, H. R.:
Experimental Evaluation of Lateral Buckling Loads,
J. Eng. Mech. Div., Proc. ASCE, Vol. 103, No. EM2,
pp. 331-337, March/April 1977.
JABEE用にすべての提出レポートをスキャナーに読み込んで 保存するという作業は、あまりにもしんどくてもうこりごりなので、 07年度は最初から電子ファイルで提出してもらおうか。 で、大型ディスプレイの左半分に提出されたレポートを表示させておいて、 右側半分に返信メールの編集画面を表示させておいて、 その場で、コピペしながら返信してレポート添削という運用にしたい。 で、私のメインマシンのLinux上で、ストレスなく表示できるように (建前上は、学生に 特定の会社の有償ソフトを買わないと作成できない ワード形式のファイルなどを強いてはいけない ということで) 提出形式は、 (パソコンがある程度以上 使える人なら) フリーのツールだけで作成できるpdfかOpenDocument ということにしたい。
大学のときに受けた理科教育の授業で、 生徒の勘違いや間違った解答の典型例のことを egにバー(上線)をつけて「エグバー」と呼んでいたのだけど、 これは理科教育のちゃんとした用語ではないのだろうか。 検索してもなかなか見つからない。
勘違い例1: 「引張ヤング率と曲げヤング率は違う。
なぜなら、引っ張る方向によって変形しやすさが違うのは、
(プラスチックの)定規を使っても明らか」
上の文章が勘違いだということの意味を
「引張ヤング率と曲げヤング率は同じ」と捉える人が
いるようなので、念のため、補足。
もちろん、引張ヤング率と曲げヤング率は
やや違う。
ただ、その違いは、木材のような引張ヤング率と曲げヤング率の
違いが大きい材料でもせいぜい1割とかそんなものだ。
その程度の違いによって、
「引張ヤング率よりも曲げヤング率が小さいから、
引っ張るよりも曲げた方が変形させやすいのだ」
と考えるのはおかしい。
例えば、引張ヤング率と曲げヤング率とでほとんど差の出ないような
(それこそプラスチックの定規のような)
棒でも、引っ張るのと曲げるのとでは、曲げた方が
はるかに大きい変形を出せる。