注意：
このページの数式は、
MathJaxを使って書いてます。
数式部分がおかしい場合は、更新ボタンをクリックすると
改善するかも知れません。
太文字のギリシャ文字($\mathbf{\varepsilon}$など)が、
太文字になっていない($\varepsilon$)かもしれません。
印刷版で確認して下さい。
その他、おかしい記述があると思ったら、
メールなどで指摘して下さい。
物体に外力が加わると物体は移動したり変形したり(曲がったりゆがんだり)する。
物体の変形量を表す準備として、
まずは物体の中の任意の点の移動量を表す方法から説明する。
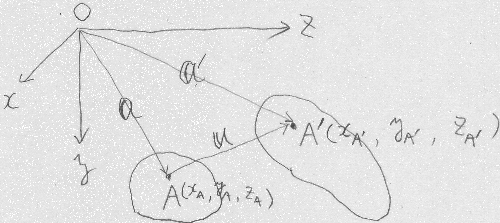
今、まだ外力を受けずに変形していない物体
(この状態を初期状態と呼ぶ)の中のある点$A$に印を付けた後に
外力を加えたら、物体は変形しながら移動し、
印をつけたところが点$A'$のところまで移動してつりあって
静止したとする。
点$A$の位置ベクトルを$\mathbf{a}=(x_{A}, y_{A}, z_{A})$,
点$A'$の位置ベクトルを$\mathbf{a'}=(x_{A'}, y_{A'}, z_{A'})$
とする。
このテキストでは、ベクトルやテンソル(後述)は、
$\mathbf{a}$のように太字で表すことにする。
手書きする場合は、文字の一部を二重線で書くこととし、
$\vec{a}$みたいにいちいち矢印を付ける表記は使わない。
さて、
最初、点$A (x_{A}, y_{A}, z_{A})$にあった点が、
物体が外力を受けて変形・移動した後に、
どの位置まで動いたかという移動量を、
変形・移動前の座標値
$(x_{A}, y_{A}, z_{A})$
の関数として
$\mathbf{u}(x_{A}, y_{A}, z_{A})=\mathbf{a'}-\mathbf{a}$
で定義されるベクトル$\mathbf{u}$で表し、これを点$A$の変位ベクトルと呼ぶ。
もちろん、ここでは点$A$の変形・移動後の点$A'$の座標値も与えてしまっているから、
$\mathbf{u}(x_{A}, y_{A}, z_{A})=\mathbf{a'}-\mathbf{a}=
(x_{A'}-x_{A}, y_{A'}-y_{A}, z_{A'}-z_{A})$
のように書けてしまうけど、
普通の構造力学の問題では、
初期状態における点$A$が、変形後にどこに移動するのかは
(問題を解いてみるまでは)分からないので、
点$A$の移動量を移動前の点$A$の座標値の関数として与えると便利なのである
(流体とかの問題だとまた事情が違ってくる)。
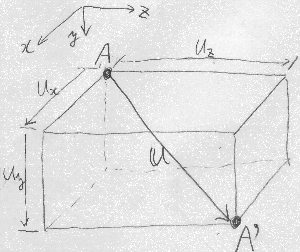変位ベクトル$u$の$x,y,z$方向成分は、
$\mathbf{u}=(u_{x}, u_{y}, u_{z})$
と表せるが、
$u_{x}$は$x$方向変位、$u_{y}$は$y$方向変位、$u_{z}$は$z$方向変位と呼ぶ。
任意点$(x,y,z)$の変位ベクトルは、$(x,y,z)$の関数として$\mathbf{u}(x,y,z)$
と表せるが、その$x,y,z$方向成分もそれぞれ$(x,y,z)$の関数なので、
$\mathbf{u}(x,y,z)=(u_{x}(x,y,z), u_{y}(x,y,z), u_{z}(x,y,z))$
と表せることになる。
$x$方向変位$u_{x}$, $y$方向変位$u_{y}$, $z$方向変位$u_{z}$は、
$x, y, z$の関数であるから、ある点の$(x,y,z)$を代入すると
1つの数値(移動距離)を取るが、正の値の時はそれぞれ$x,y,z$軸の正の
方向への移動距離を表すし、負の値の時はそれぞれ$x,y,z$軸の負の方向への
移動距離を表すから、1つの軸上で正か負かの向きの区別がある
1次元ベクトルと見なせる。
だから、
このテキストの中で
$u_{x}$, $u_{y}$, $u_{z}$を図示する際には、
移動距離が正になる方向に矢印をつけてベクトル的に図示するが、
1次元ベクトルは、あくまでスカラー(後述)なので、
数式として書く場合は太字では書かない。
ここで、物体の「変形・移動」というような書き方をしているが、
「変形」と「移動」というのは同じではない。
物体に外力が加わって、物体全体としての位置はほとんど「移動」せずに
その場でぐにゃっと曲がったりゆがんだりして「変形」することもあれば、
物体全体の形は「変形」せずに、位置がすごく離れた場所まで「移動」する
こともある。
「変位」というのは、物体の変形・移動前後の点の移動量を表しているが、
その移動量の中には、変形成分も移動成分も含まれている。
全く変形しない(と仮想的に考えた)物体を剛体というが、
剛体は外力を受けても変形はせずに移動しかしない。
そのような純粋な移動だけからなる変位は「剛体変位」と呼ばれる。
これから、物体内部の変形を、物体中の点の座標値との関係で
(変位ベクトルを使って)表していこうとしているのだけど、
それにさきだって、まず、
物体の中に各辺が座標軸と平行な微小な立方体(2次元なら正方形)の要素を
考えて、その四角い要素がどのように変形するかということに
着目してみる。
簡単のため2次元で考えるとして、
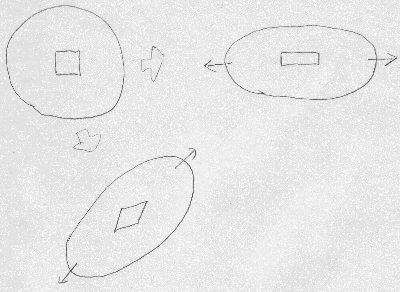
例えば、図のような物体が左右に引っ張られたとして、
微小正方形要素の周辺が$z$軸方向には一様に伸び、
$y$方向には一様に縮んだとすると、
正方形要素は、頂点の直角を保ったまま長方形に変形する。
このように、物体中の微小な立方体(2次元なら正方形)要素が、
頂点の直角を保ちながら、直方体(2次元なら長方形)に変形するような変形を、
ここでは「伸び縮み変形」と呼んでおく。
一方、図のような物体を微小正方形の対角線方向に斜めに引っ張ったら、
微小正方形要素は、頂点の直角がくずれて、ひし形に変形するだろう。
このように物体中の微小な立方体(2次元なら正方形)要素が、
(辺の長さは変えずに)頂点の角度を変えるような変形を「せん断変形」と呼ぶ。
すると、これ以外の一般的な変形
(図の微小正方形が不等辺の平行四辺形になるような)も、
「伸び縮み変形」と「せん断変形」の組合せとして表せそうだ。
上の例では、微小正方形要素の各辺が座標軸と平行になるような要素を
考えることにしたが、もし微小正方形要素を45°回転させたら、
今度は、左右に引っ張るとせん断変形して、
右上と左下の斜め方向に引っ張ると伸び縮み変形するようにもできる。
つまり、伸び縮み変形とかせん断変形というのは、
どの座標系で観測するかに依存して変わってくるものであるし、
逆に言うと、どんな変形状態でも伸び縮み変形として捉えることのできる
向きがあることになる(この辺の話は「主ひずみ」の話をする機会が
あれば後述)。
さて、物体中の微小正方形要素が、各頂点の直角を保ちながら長方形に
変形する
伸び縮み変形の変形量を
変位ベクトルの成分を使って表してみる。
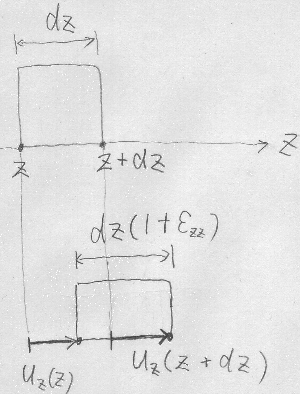
今、初期状態の物体の中に
2辺が$y,z$軸に平行で、一辺の長さが$dz$の微小正方形要素を考える。
物体が外力を受けて変形・移動したら、
この正方形要素が$z$軸方向に伸びて、
初期状態の1辺の長さが$dz$から$z$方向に$1+\varepsilon_{zz}$倍 長くなったとすると、
この$\varepsilon_{zz}$を$z$方向の「伸びひずみ」と言うのだけど、
この伸びひずみ$\varepsilon_{zz}$を、$z$方向変位$u_{z}$を使って
表したい。
初期状態の正方形の左下の点の座標が$z$だったとすると、
初期状態の正方形の右下の点の座標は$z+dz$になる。
微小要素の左下の点の$z$方向変位は初期状態の座標値$z$の関数として
$u_{z}(z)$と表され、
微小要素の右下の点の$z$方向変位は初期状態の座標値$z+dz$の関数として
$u_{z}(z+dz)$と表される。
これらを使って変形後の微小要素の$z$方向の長さ$dz(1+\varepsilon_{zz})$を
表してみると、
$dz(1+\varepsilon_{zz})=dz+u_{z}(z+dz)-u_{z}(z)$
と書ける。これを変形すると、
$\varepsilon_{zz}=\frac{u_{z}(z+dz)-u_{z}(z)}{dz}$
と書けるが、
これは$dz$がじゅうぶんに微小だという仮定のもとでの
ひずみのおおざっぱな定義である。
微小要素の1辺の長さ$dz$を極限まで小さくしてやると
これは「微分」の定義になるので、
ある点$(x,y,z)$の
$z$方向の伸びひずみは次式のように$z$方向変位の$z$に関する微分として
定義できる。
${\displaystyle \varepsilon_{zz}(x,y,z)=\lim_{dz \to 0}\frac{u_{z}(z+dz)-u_{z}(z)}{dz}
=\frac{\partial u_{z}}{\partial z}}$
同様に
ある点$(x,y,z)$の
$x$方向の伸びひずみ$\varepsilon_{xx}$は$x$方向変位の$x$に関する微分として、
$y$方向の伸びひずみ$\varepsilon_{yy}$は$y$方向変位の$y$に関する微分として、
$\varepsilon_{x x}(x,y,z)
=\frac{\partial u_{x}}{\partial x}$
$\varepsilon_{yy}(x,y,z)
=\frac{\partial u_{y}}{\partial y}$
と定義できる。
微分を偏微分で書いたのは、$u_{z}$などの変位成分は、
実際には$x,y,z$の関数だからである。
だから、厳密には$u_{z}(z+dz)$とかも、
$u_{z}(x,y,z+dz)$みたいな書き方をすべきだろうが、
$z$軸に平行な軸の1次元上の議論では、$x,y$は常に
同じ値なので省略した。
今後も、簡単のため適宜、このような省略を行うことが多々ある。
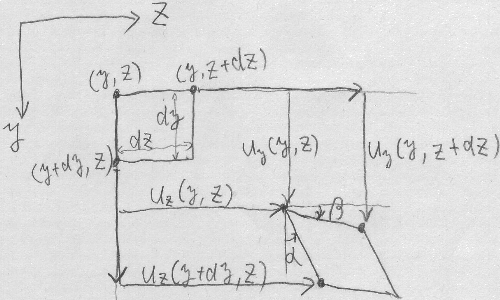初期状態の
物体の中にあった微小な長方形要素が、
物体が外力を受けて変形・移動したら、
図のように2辺の長さ(縦が$dy$, 横が$dz$)を変えずに、
頂点の角度が変わって平行四辺形になったとする。
正方形要素ではなく長方形要素にしたのは、
回転量を定義するときに縦横の区別がないと不都合だから。
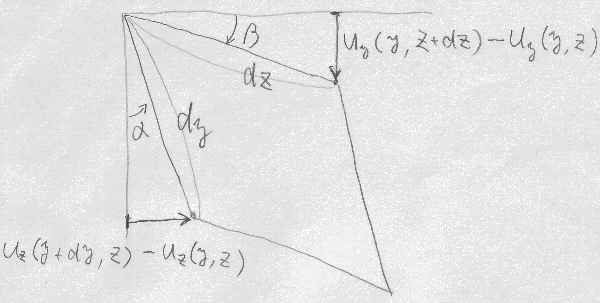さて、もともと直角だった長方形要素の左上の頂点の角度が、
どれだけの角度だけつぶれたのかを変位ベクトル(各頂点の$y,z$方向変位)を
用いて示したい。
角度が小さいときは、$\sin\theta\cong\theta$となることから、
$\alpha\cong\sin\alpha=\frac{u_{z}(y+dy,z)-u_{z}(y,z)}{dy}$
$\beta\cong\sin\beta=\frac{u_{y}(y,z+dz)-u_{y}(y,z)}{dz}$
と書ける。
微小要素の2辺の長さ、$dy, dz$を極限まで小さくしていけば、
これは「微分」の定義になるので、ある点$(x,y,z)$
(を左上の頂点とする微小長方形要素)の角度変化$\alpha$と$\beta$は、
それぞれ$z$方向変位の$y$に関する微分、
$y$方向変位の$z$に関する微分として次のように定義できる。
${\displaystyle \alpha(x,y,z)=\lim_{dy \to 0}\frac{u_{z}(y+dy,z)-u_{z}(y,z)}{dy}
=\frac{\partial u_{z}}{\partial y}}$
${\displaystyle \beta(x,y,z)=\lim_{dz \to 0}\frac{u_{y}(y,z+dz)-u_{y}(y,z)}{dz}
=\frac{\partial u_{y}}{\partial z}}$
微分が偏微分になっているのは、$x,y,z$の関数である$u_{z}$
や$u_{y}$を$y$だけの関数とみなして微分したり、
$z$だけの関数とみなして微分したから。
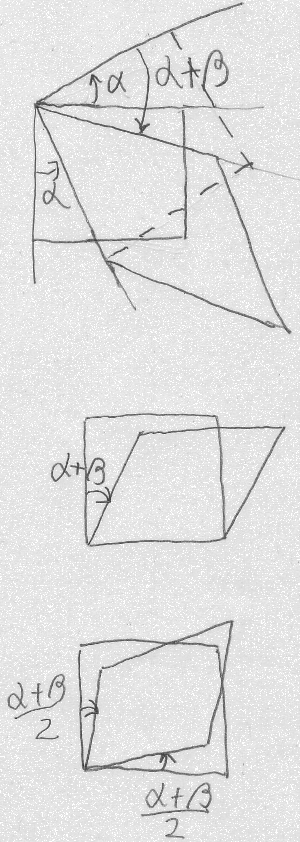さて、角度変化$\alpha$と$\beta$は、
初期状態で直角をなしていた2辺が、それぞれ内側にどれだけつぶれたかを
示している訳だけど、
$\alpha$か$\beta$の単独では、それが実質的な角度変化を表しているのか
どうかは分からない。例えば、図のように、長方形要素が最初$\alpha$だけ
剛体的に回転して
(このような回転に関する「剛体変位」を「剛体回転」という)、
そのあとに上の辺の側だけが$\alpha+\beta$だけつぶれて実質的な変形をしたのかも知れない
(もちろん、最終状態が同じになるような剛体回転と実質変形の組み合わせはこの他にもいくらでも考え得る)。
つまり、初期状態で直角だった角度がどれだけ実質的につぶれたのかを表すには、
$\alpha +\beta$のように2辺の内側へのつぶれ具合を表す角度の足し算にする
必要があるようだ。
この
$\alpha+\beta$
のことを工学せん断ひずみと呼び、
記号としては
$\gamma$
などを用いる。
この実質的な角度変化量$\alpha+\beta$を
2辺が同じ角度だけ内側に変形してつぶれたように振り分けるなら
$\frac{\alpha +\beta}{2}$
となるが、
$\frac{\alpha +\beta}{2}$
のことをせん断ひずみと呼び、
記号としては、
$yz$
面のせん断変形を表すせん断ひずみなら
$\varepsilon_{yz}$や$\varepsilon_{zy}$
と表す。
このように、せん断ひずみの定義には2種類あるので、注意が必要である。
以上から、$yz$面内のせん断変形を表すせん断ひずみ$\varepsilon_{yz}$を
$(x,y,z)$の関数として次式のように定義できる。
$\varepsilon_{yz}=\frac{\alpha +\beta}{2}=\frac{1}{2}
(\frac{\partial u_{y}}{\partial z}
+
\frac{\partial u_{z}}{\partial y})
$
同様に、
$zx$面内のせん断変形を表すせん断ひずみ$\varepsilon_{zx}$や
$xy$面内のせん断変形を表すせん断ひずみ$\varepsilon_{xy}$についても
$(x,y,z)$の関数として次式のように定義できる。
$\varepsilon_{zx}=\frac{1}{2}
(\frac{\partial u_{z}}{\partial x}
+
\frac{\partial u_{x}}{\partial z})
$
$\varepsilon_{xy}=\frac{1}{2}
(\frac{\partial u_{x}}{\partial y}
+
\frac{\partial u_{y}}{\partial x})
$
伸びひずみの定義と
せん断ひずみの定義を組み合わせると、
物体の任意点$(x,y,z)$のひずみを
$(x,y,z)$の関数として
$\varepsilon_{ij}=\frac{1}{2}
(\frac{\partial u_{i}}{\partial x_{j}}
+
\frac{\partial u_{j}}{\partial x_{i}})
(但し i,j=x,y,z またx_{1}=x, x_{2}=y, x_{3}=z)
$
のように
$\varepsilon_{x x},
\varepsilon_{xy},
\varepsilon_{xz},
\varepsilon_{yx},
\varepsilon_{yy},
\varepsilon_{yz},
\varepsilon_{zx},
\varepsilon_{zy},
\varepsilon_{zz}$
の9個の成分を、$i,j$の添字を使って1つの記号で表すことができる。
ちなみに定義から、
$\varepsilon_{xy}=\varepsilon_{yx}$,
$\varepsilon_{yz}=\varepsilon_{zy}$,
$\varepsilon_{zx}=\varepsilon_{xz}$
である。
この9個の成分を行列表示したり、添字を用いた演算のわかりやすさのため、
$i,j=x,y,z$を$i,j=1,2,3$と置き換えて、
$x_{1}=x, x_{2}=y, x_{3}=z$と置き換えて、
$\varepsilon_{x x},
\varepsilon_{xy},
\varepsilon_{xz},
\varepsilon_{yx},
\varepsilon_{yy},
\varepsilon_{yz},
\varepsilon_{zx},
\varepsilon_{zy},
\varepsilon_{zz}$
の9個の成分を、
$\varepsilon_{11},
\varepsilon_{12},
\varepsilon_{13},
\varepsilon_{21},
\varepsilon_{22},
\varepsilon_{23},
\varepsilon_{31},
\varepsilon_{32},
\varepsilon_{33}$
と表す場合も多いが、その場合、
伸びひずみの定義と
せん断ひずみの定義を組み合わせた
物体の任意点のひずみは、
$\varepsilon_{ij}=\frac{1}{2}
(\frac{\partial u_{i}}{\partial x_{j}}
+
\frac{\partial u_{j}}{\partial x_{i}})
(但し i,j=1,2,3)
$
と表される。
このように複数の添字を使って(配列として)表される量のことを
「テンソル」と言う。
添字$i,j$を用いて定義される上記のひずみはテンソルと言えるので、
「ひずみテンソル」と呼ばれる。
上の「ひずみテンソル」の場合、添字が2つあるため、
2階のテンソルと呼ばれる。
添字が1つで表現できるベクトル(例えば力とか変位ベクトルとか)は
1階のテンソルである。
1つの数値として表現できる量(例えば質量とか$x$方向変位とか)は
0階のテンソルであり、「スカラー」と呼ばれる。
スカラーは正負の値を取る普通の数値だから、
「$x$方向変位」など1つの軸上で考えると(数直線上で)正負の方向を持つと
見なすこともできるので「1次元ベクトル」と
して扱うこともある。
$a_{ij}$を成分とするテンソルは$i$行$j$列の行列$\mathbf{a}$として
表現することができる。
テンソルやベクトルを1文字の記号で表すときは$\mathbf{a}$
のように太字で(後藤の手書きの場合は文字の1部を二重線にして)表すが、
添字を付けて成分に着目して表記するときは太字にせずに
$a_{ij}$のように書く(例えば、$i,j$に具体的な数値を代入した$a_{23}$
とかはスカラーなので)。
という訳で、ひずみテンソル$\mathbf{\varepsilon}$を行列で表示すると、
$
[\mathbf{\varepsilon}]
=
\left[
\begin{array}{ccc}
\varepsilon_{x x} & \varepsilon_{xy} & \varepsilon_{xz}\\
\varepsilon_{yx} & \varepsilon_{yy} & \varepsilon_{yz}\\
\varepsilon_{zx} & \varepsilon_{zy} & \varepsilon_{zz}
\end{array}
\right]
$
と表せる。
ギリシャ文字は太文字にならないようなので、テンソルの場合は
$[\varepsilon ]$みたいに表しておく。
$a_{ij}=a_{ji}$となる行列は
(行列表示したときに対角項$a_{ii}$を対称軸として
対称な位置にある成分どうしが等しくなることから)
対称行列と呼ばれる。
前述したように定義から、
$\varepsilon_{xy}=\varepsilon_{yx}$,
$\;\varepsilon_{yz}=\varepsilon_{zy}$,
$\;\varepsilon_{zx}=\varepsilon_{xz}$
なので、ひずみテンソルは対称行列で表される。
この場合、ひずみテンソルは対称テンソルと呼ばれる。
さて、ひずみの次元は、伸びひずみであれせん断ひずみであれ、
定義からわかるように無次元である。
このテキストで「ひずみ」と言うときは、
ひずみテンソル成分である伸びひずみやせん断ひずみなどの無次元量の
ことであり、それは一般的な物理の分野の使われ方だと思う。
ところで、
土木ではほとんど使われないとは思うが、
建築などの分野では、
上記の「ひずみ」の意味で「ひずみ度」という語を用い、
ひずみを生じた変形量(例えば棒の伸びた長さとか)の意味で
「ひずみ」という語を用いるという紛らわしい
使い分けをする習慣も一部にあるようなので(こうした表現に
出会ったときに混乱しないための予備知識として)参考までに記しておく。
土木の分野でも見受けられる「応力度」という紛らわしい表現については
応力-ひずみ関係参照。
メモ:
$\mathbf{\varepsilon}$とか、ギリシャ文字の
太字が太字になっていないかもしれない。
$\alpha$,
$\mathbf{\alpha}$, $\beta$, $\mathbf{\beta}$
