
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
第5回で、断面の
曲げモーメントとたわみの関係が
$M(z)=-EIv''(z)$
と表されることが示された。
曲げモーメント$M(z)$がたわみ$v(z)$の2階微分で表されているということは、
曲げモーメント分布が力のつりあいで求まる静定梁なら、
これを$z$について2回積分すればたわみ$v(z)$を$z$の関数として求めることが
できそうである。
 ということで、
構造力学I第6回で
曲げモーメント$M(z)$を求めた片持ち梁のたわみ$v(z)$を求めてみよう。
曲げ剛性は$EI$とする。
構造力学I第6回で、
ということで、
構造力学I第6回で
曲げモーメント$M(z)$を求めた片持ち梁のたわみ$v(z)$を求めてみよう。
曲げ剛性は$EI$とする。
構造力学I第6回で、
$M(z)=-P(\ell -z)\;\;\;\;(0\le z\le\ell)$ と求まっているから、
$M(z)=-EIv''(z)$ にこれを代入すれば、$-P(\ell -z)=-EIv''(z)$となる。
左右を入れ替えて、$(z)$を省略すると、
$EIv''=P(\ell-z)$ となる。
$M(z)$は、$(0\le z\le\ell)$で1つの式で表されて場合分けはないから、
この微分方程式が、$(0\le z\le\ell)$で成り立つと考えられる。
つまり、この式をそのまま場合分けせずに積分していけばいいだろう。
まずこれを1回積分すると、
$EIv'=P(\ell z-\frac{z^{2}}{2})+A$ ここに$A$は積分定数。もう1回積分すると、
$EIv=P(\frac{\ell}{2}z^{2}-\frac{z^{3}}{6})+Az+B$ ここに$B$は積分定数。
 $A, B$の値を決めるには、境界条件というのを使う。
時間に関する微分方程式では、初期条件から積分定数を決めたりしたと思うが、
それと同じように、梁の問題では、支承で固定されている点のたわみが0といった
条件が使える。
このように境界条件を与えて微分方程式を解く問題を
境界値問題と言う。
ちなみに、初期値を与えて微分方程式を解く問題は初期値問題。
$A, B$の値を決めるには、境界条件というのを使う。
時間に関する微分方程式では、初期条件から積分定数を決めたりしたと思うが、
それと同じように、梁の問題では、支承で固定されている点のたわみが0といった
条件が使える。
このように境界条件を与えて微分方程式を解く問題を
境界値問題と言う。
ちなみに、初期値を与えて微分方程式を解く問題は初期値問題。
この場合、左端の$z=0$が固定端となっており、ここでたわみは発生しないので、
$v(0)=0$となる。
積分定数は、$A, B$の2個なので、これらを決定するには、
もう一つ条件がいる。
固定端の場合、図のように、固定端部で梁は$z$軸に接するように変形する。
つまり、固定端部では、たわみの傾き$v'(z)$が0となる。
つまり、この場合は、左端$z=0$で$v'(0)=0$である。
また、後で説明するが、ある点でのたわみ$v(z)$の傾き$v'(z)$は、その点での
梁の回転量を表すことからたわみ角と言う。
たわみ角をこの座標の$x$軸右ねじまわり回転角$\theta_{x}$として定義するなら、
$z$が正方向に増えたときに、$v$が$y$の正方向に増えると、
時計回り($x$軸左ねじ回り)になるので、$\theta_{x}=-v'$となるが、
境界条件を使うときは、$v'=0$とおくだけなので、
たわみ角の符号は気にしなくてよい。
境界条件:$v(0)=0, v'(0)=0$
まず、$v'(0)=0$より、
$EIv'(0)=P(\ell\cdot 0-\frac{0^{2}}{2})+A=0\;\;$
よって、$A=0$
次に、$v(0)=0$より、
$EIv(0)=P(\frac{\ell}{2}\cdot 0^{2}-\frac{0^{3}}{6})+A\cdot 0+B\;\;$
よって、$B=0$
よって、$v(z)=\frac{P}{6EI}(3\ell z^{2}-z^{3})\;\;$
先端のたわみ:$v(\ell)=\frac{P\ell^{3}}{3EI}$
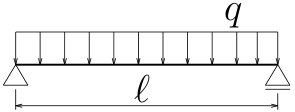 では、
構造力学第7回で
曲げモーメント$M(z)$を求めてある等分布荷重を受ける単純梁のたわみを
求めてみよう。
曲げ剛性は$EI$とする。
曲げモーメントは、
構造力学第7回で求めたように、
では、
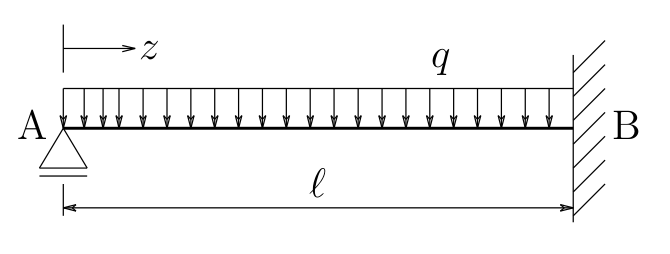
構造力学第7回で
曲げモーメント$M(z)$を求めてある等分布荷重を受ける単純梁のたわみを
求めてみよう。
曲げ剛性は$EI$とする。
曲げモーメントは、
構造力学第7回で求めたように、
$M=\frac{q}{2}(\ell z-z^{2})\;\;\;(0\le z\le\ell)$
とこれも$(0\le z\le\ell)$で1つの式で表されるから、場合分けせずに、
そのまま積分できる。
$M=-EIv''$より
$EIv''=\frac{q}{2}(z^{2}-\ell z)$
$EIv'=\frac{q}{2}(\frac{z^{3}}{3}-\frac{\ell }{2}z^{2})+A$
$EIv=\frac{q}{2}(\frac{z^{4}}{12}-\frac{\ell }{6}z^{3})+Az+B$
境界条件は、両端$z=0$と$z=\ell$に支承があり、ここはたわまないので、
$v(0)=0, v(\ell )=0$である。
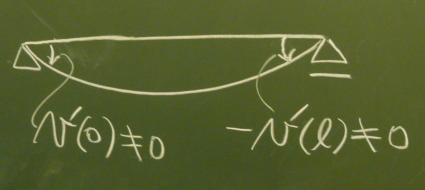 ちなみに、ヒンジ支承、ローラー支承は、回転できるから、支承の
たわみ角
$v'(0), v'(\ell )$は0にはならない。
ちなみに、
$v'$は、$z$が正方向に増える際に、$v$が$y$の正方向に増える傾きだから、
図の左端の時計回り回転角は$v'$だが、
図の右端の反時計回り回転角は$-v'$になる。とはいえ、
境界条件を考える時は、
$v'=0$とおくだけなので、$v'$の向きや符号は気にしなくてよい。
$v(0)=0, v(\ell )=0$だけで既に境界条件は2つあるから、$A, B$が求まる。
ちなみに、ヒンジ支承、ローラー支承は、回転できるから、支承の
たわみ角
$v'(0), v'(\ell )$は0にはならない。
ちなみに、
$v'$は、$z$が正方向に増える際に、$v$が$y$の正方向に増える傾きだから、
図の左端の時計回り回転角は$v'$だが、
図の右端の反時計回り回転角は$-v'$になる。とはいえ、
境界条件を考える時は、
$v'=0$とおくだけなので、$v'$の向きや符号は気にしなくてよい。
$v(0)=0, v(\ell )=0$だけで既に境界条件は2つあるから、$A, B$が求まる。
境界条件:$v(0)=0, v(\ell )=0\;\;$
まず、$v(0)=0$より
$EIv(0)=\frac{q}{2}(\frac{0^{4}}{12}-\frac{\ell }{6}\cdot 0^{3})+A\cdot 0+B=0\;\;\;\;$よって、$B=0$
次に、$v(\ell)=0$より
$EIv(\ell)=\frac{q}{2}(\frac{\ell^{4}}{12}-\frac{\ell }{6}\ell^{3})+A\ell+0=0\;\;$
よって、
$A=\frac{q\ell^{3}}{24}$
よって、
${\displaystyle v=\frac{q}{24EI}(z^{4}-2\ell z^{3}+\ell^{3}z)}$
中央のたわみ: ${\displaystyle v\left(\frac{\ell }{2}\right)=\frac{5q\ell^{4}}{384EI}}$
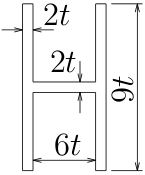 この梁の断面が、図のようなH型をしていたとして、
このとき、断面に生じる最大の直応力$\sigma_{zz}$を求めてみたい。
構造物が外力を受けた場合に、材料が破壊するかどうかというのは、
応力を調べることで判断できるので、
最大の応力が発生している場所と大きさを見極めるのは
重要なことである。
曲げモーメント$M(z)$は既にわかっているので、
応力を求めるには、
第5回で導いた
この梁の断面が、図のようなH型をしていたとして、
このとき、断面に生じる最大の直応力$\sigma_{zz}$を求めてみたい。
構造物が外力を受けた場合に、材料が破壊するかどうかというのは、
応力を調べることで判断できるので、
最大の応力が発生している場所と大きさを見極めるのは
重要なことである。
曲げモーメント$M(z)$は既にわかっているので、
応力を求めるには、
第5回で導いた
${\displaystyle \sigma_{zz}(y,z)=
\frac{M(z)}{I}y}$
の関係を用いればよい。まず、断面2次モーメントは、
第6回でやった
長方形の公式($\frac{bh^{3}}{12}$)を利用するとすると、
両端の縦に細長い長方形2つと、真ん中の薄っぺらい長方形1つの
足し算と考えて、
$I=\frac{2t(9t)^{3}}{12}\times 2 +\frac{6t(2t)^{3}}{12}=247t^{4}$
$\sigma_{zz}$が最大になるのは、
$M(z)$と$y$が最大になるところだ。
$y$の(絶対値の)最大値は、断面の高さが$9t$で、
このH型断面の図心は上下対称で真ん中だから、
一番下の$y=\frac{9}{2}t$と
一番上の$y=-\frac{9}{2}t$だ。
$M(z)$の最大値は、
第7回のモーメント図を見て
判断すると、真ん中$z=\frac{\ell}{2}$の箇所とわかる。
つまり$M_{max}=M(\frac{\ell }{2})=\frac{q\ell^{2}}{8}$
$\sigma_{zz}=\frac{M}{I}y$より
$\sigma_{zz}(y=-\frac{9}{2}t, z=\frac{\ell }{2})
=\frac{\frac{q\ell^{2}}{8}}{247t^{4}}(-\frac{9}{2}t)
=-\frac{9q\ell^{2}}{3952t^{3}}$
$\sigma_{zz}(y=\frac{9}{2}t, z=\frac{\ell }{2})
=\frac{9q\ell^{2}}{3952t^{3}}$
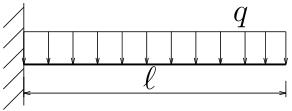 では、等分布荷重を受ける片持ち梁のたわみも求めてみよう。
曲げ剛性は$EI$とする。
曲げモーメントは、各自、自力で求めること。
ちなみに、過去の構造力学Iの小テストの回答は
ここ。
たわみまで求めているのはここ。
では、等分布荷重を受ける片持ち梁のたわみも求めてみよう。
曲げ剛性は$EI$とする。
曲げモーメントは、各自、自力で求めること。
ちなみに、過去の構造力学Iの小テストの回答は
ここ。
たわみまで求めているのはここ。
$M=-\frac{q}{2}(z-\ell )^{2}$
$M=-EIv''$より
$EIv''=\frac{q}{2}(z^{2}-2\ell z+\ell^{2})$
$EIv'=\frac{q}{2}(\frac{z^{3}}{3}-\ell z^{2}+\ell^{2}z)+A$
$EIv=\frac{q}{2}(\frac{z^{4}}{12}-\frac{\ell }{3}z^{3}+\frac{\ell^{2}}{2}z^{2})
+Az+B$
境界条件: $v'(0)=0, v(0)=0$より
$A=0, B=0$
$v=\frac{q}{24EI}(z^{4}-4\ell z^{3}+6\ell^{2}z^{2})$
先端のたわみ: $v(\ell )=\frac{q\ell^{4}}{8EI}$
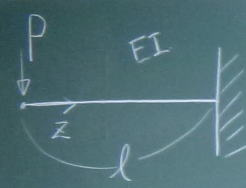 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
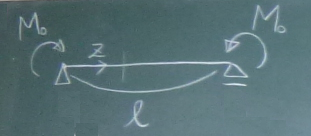 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
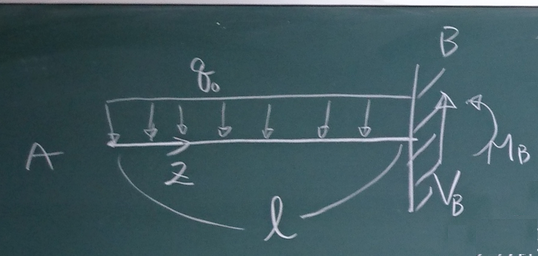
 図のように
左端ローラー支承、右端固定で等分布荷重$q$を受ける不静定梁について、
左端を原点として、梁軸に沿って右向き正に
座標$z$を取る。
この梁は不静定梁なので、力のつりあいから曲げモーメントを求めることは
できないが、
この梁の曲げモーメントは
次式で与えられるものとする。
図のように
左端ローラー支承、右端固定で等分布荷重$q$を受ける不静定梁について、
左端を原点として、梁軸に沿って右向き正に
座標$z$を取る。
この梁は不静定梁なので、力のつりあいから曲げモーメントを求めることは
できないが、
この梁の曲げモーメントは
次式で与えられるものとする。
$M(z)=
\frac{q}{8}(-4z^{2}+3\ell z)\;\;\;\;(0\le z\le \ell)$
不静定梁ではあるが、曲げモーメントがわかっているので、
$M=-EIv''$を積分すれば、たわみを求めることができる。
たわみ$v(z)$を求めよ。
曲げ剛性は$EI$とする。
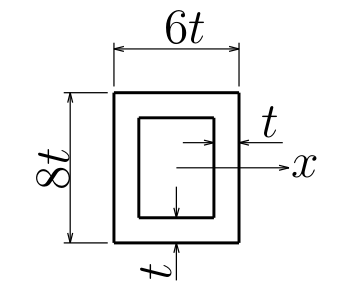 梁の断面が図のような二軸対称な箱型断面をしているとき、
この箱型断面の中立軸回りの断面2次モーメント$I_{x}$を求め、
固定端部Bの断面に作用する最大の引張応力$\sigma_{\text{t}}^{\text{B}}$を求めよ。
答えはここ。
梁の断面が図のような二軸対称な箱型断面をしているとき、
この箱型断面の中立軸回りの断面2次モーメント$I_{x}$を求め、
固定端部Bの断面に作用する最大の引張応力$\sigma_{\text{t}}^{\text{B}}$を求めよ。
答えはここ。
これは、2013年度の期末試験。
2022年度小テスト:
小テスト221130
2021年度小テスト:
問,
解答
2020年度小テスト:
問1,
解答
メモ: