
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
前回は、 今後、公式として使うであろう大事な式がいっぱい 出てきたが、軸力や曲げモーメントを求めるために、 断面の応力を面積積分すると、 $y$や$y^{2}$の積分が出てくるので、 断面1次モーメント$J_{x}$や断面2次モーメント$I$という断面定数が出てきた。 これは、とても大事な量であるが、 具体的にどのように計算するのか、いくつかの例を以下に示す。
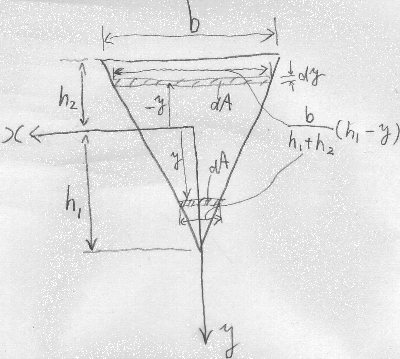 図のような二等辺三角形の対称軸に$y$軸を取り、
$x$軸を三角形の図心とは一致しない適当な位置に取った場合に、
この三角形の$x$軸回りの断面1次モーメントを求めてみたい。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
まず、$x$軸より下側の小さい方の微小部分について考えると、
この微小部分の横幅は、
この横幅を底辺とするさきっちょの小さい三角形と、
全体の大きい三角形が相似であることから求まる。
それぞれの三角形の底辺と高さの比から
図のような二等辺三角形の対称軸に$y$軸を取り、
$x$軸を三角形の図心とは一致しない適当な位置に取った場合に、
この三角形の$x$軸回りの断面1次モーメントを求めてみたい。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
まず、$x$軸より下側の小さい方の微小部分について考えると、
この微小部分の横幅は、
この横幅を底辺とするさきっちょの小さい三角形と、
全体の大きい三角形が相似であることから求まる。
それぞれの三角形の底辺と高さの比から
$微小部分の横幅:小さい三角形の高さ(h_{1}-y)=
大きい三角形の横幅b:大きい三角形の高さ(h_{1}+h_{2})$
よって、
この微小部分の横幅は、
$\frac{b}{h_{1}+h_{2}}(h_{1}-y)$と求まる
($y$は微小部分が$x$軸より上にある場合は負の値を取るので、この式は
微小部分が$x$軸より上にあっても成り立つ)。
微小部分の面積を$dA=\frac{b}{h_{1}+h_{2}}(h_{1}-y)dy$と置くと、
$x$軸まわりの断面1次モーメントは、
$J_{x}=\int_{A}ydA$
$=\int_{-h_{2}}^{h_{1}}y\frac{b}{h_{1}+h_{2}}(h_{1}-y)dy$
$=\int_{-h_{2}}^{h_{1}}\frac{b}{h_{1}+h_{2}}(h_{1}y-y^{2})dy$
$=\frac{b}{h_{1}+h_{2}}[\frac{h_{1}y^{2}}{2}-\frac{y^{3}}{3}]_{-h_{2}}^{h_{1}}$
$=\frac{b}{h_{1}+h_{2}}(
\frac{h_{1}^{3}}{2}-\frac{h_{1}^{3}}{3}-\frac{h_{1}h_{2}^{2}}{2}-\frac{h_{2}^{3}}{3}
)$
$=\frac{b}{6(h_{1}+h_{2})}(h_{1}^{3}-3h_{1}h_{2}^{2}-2h_{2}^{3})$
答えとしては、これで十分だが、図心の説明の関係上、もう少し展開してみる。
$=\frac{b}{6(h_{1}+h_{2})}
(h_{1}^{3}-h_{1}h_{2}^{2}-2h_{1}h_{2}^{2}-2h_{2}^{3})$
$=\frac{b}{6(h_{1}+h_{2})}
(h_{1}(h_{1}^{2}-h_{2}^{2})-2h_{2}^{2}(h_{1}+h_{2}))$
$=\frac{b}{6}(h_{1}(h_{1}-h_{2})-2h_{2}^{2})$
$=\frac{b}{6}(h_{1}^{2}-h_{1}h_{2}-h_{2}^{2}-h_{2}^{2})$
$=\frac{b}{6}((h_{1}+h_{2})(h_{1}-h_{2})
-h_{2}(h_{1}+h_{2}))$
$=\frac{b}{6}(h_{1}+h_{2})(h_{1}-2h_{2})$
となる。
さて、図心の$y$座標$y_{G}$を求めてみると、
$y_{G}=\frac{J_{x}}{A}$
$=\frac{\frac{b}{6}(h_{1}+h_{2})(h_{1}-2h_{2})}{\frac{b(h_{1}+h_{2})}{2}}$
$=\frac{h_{1}-2h_{2}}{3}$
となる。さて、$x$軸が図心を通っている場合、
$y_{G}=0$となるから、
$\frac{h_{1}-2h_{2}}{3}=0$から
$h_{1}=2h_{2}$となり、三角形の図心は頂点から
高さの$\frac{2}{3}$の位置にあることがわかる。
もちろん、$x$軸が図心を通ってなくても、三角形の形は変わらないから、
図心は頂点から高さの$\frac{2}{3}$の位置にある。
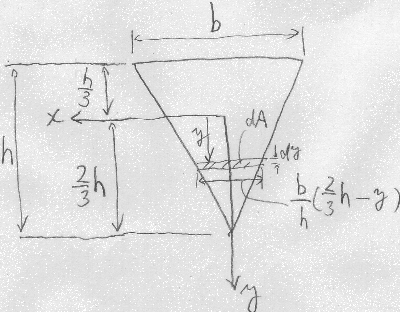 次に、$x$軸がこの三角形の図心上にある場合に、
この三角形の$x$軸まわりの断面2次モーメントを求めてみよう。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
この微小部分の横幅は、
さきほどと同様にさきっちょの小さい三角形と全体の大きい三角形の
相似関係から、
次に、$x$軸がこの三角形の図心上にある場合に、
この三角形の$x$軸まわりの断面2次モーメントを求めてみよう。
任意の$y$座標で$x$軸に平行な細長い面積$dA$の微小部分を考える。
この微小部分の横幅は、
さきほどと同様にさきっちょの小さい三角形と全体の大きい三角形の
相似関係から、
$微小部分の横幅:小さい三角形の高さ(\frac{2}{3}h-y)=
大きい三角形の横幅b:大きい三角形の高さh$
となり、
微小部分の横幅は、
$\frac{b}{h}(\frac{2}{3}h-y)$と求まる
($y$は微小部分が$x$軸より上にある場合は負の値を取るので、この式は
微小部分が$x$軸より上にあっても成り立つ)。
微小部分の面積を$dA=\frac{b}{h}(\frac{2}{3}h-y)dy$と置くと、
$x$軸まわりの断面2次モーメントは、
$I=\int_{A}y^{2}dA$
$=\int_{-\frac{h}{3}}^{\frac{2}{3}h}y^{2}\frac{b}{h}(\frac{2}{3}h-y)dy$
$=\frac{b}{h}\int_{-\frac{h}{3}}^{\frac{2}{3}h}
(\frac{2}{3}hy^{2}-y^{3})dy$
$=\frac{b}{h}[\frac{2}{3}h\frac{y^{3}}{3}-\frac{y^{4}}{4}]
_{-\frac{h}{3}}^{\frac{2}{3}h}$
$=\frac{b}{h}
(\frac{2^{4}h^{4}}{3^{5}}-\frac{2^{4}h^{4}}{4\cdot 3^{4}}
+\frac{2h^{4}}{3^{5}}+\frac{h^{4}}{4\cdot 3^{4}})$
$=\frac{bh^{3}}{3^{4}}
(\frac{16}{3}-4+\frac{2}{3}+\frac{1}{4})$
$=\frac{bh^{3}}{3^{4}}
(2+\frac{1}{4})$
$=\frac{bh^{3}}{36}$
となる。
三角形の図心軸回りの断面2次モーメントが
$\frac{bh^{3}}{36}$であることは、公式として覚えておこう。
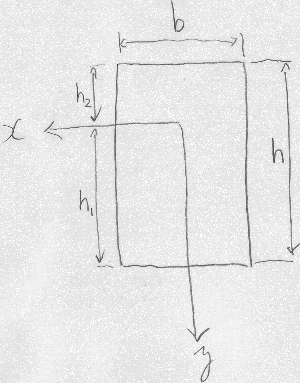 図のような長方形の$x$軸まわりの断面1次モーメントと図心の位置、
断面2次モーメントを求めよ。
また$x$軸が図心上にある場合、
長方形の
断面2次モーメントが$\frac{bh^{3}}{12}$となる
ことを示せ。
図のような長方形の$x$軸まわりの断面1次モーメントと図心の位置、
断面2次モーメントを求めよ。
また$x$軸が図心上にある場合、
長方形の
断面2次モーメントが$\frac{bh^{3}}{12}$となる
ことを示せ。
$J_{x}=\int_{A}ydA=\int_{-h_{2}}^{h_{1}}ybdy$
$=[b\frac{y^{2}}{2}]_{-h_{2}}^{h_{1}}
=\frac{b(h_{1}^{2}-h_{2}^{2})}{2}$
$I=\int_{A}y^{2}dA=\int_{-h_{2}}^{h_{1}}y^{2}bdy$
$=[b\frac{y^{3}}{3}]_{-h_{2}}^{h_{1}}
=\frac{b(h_{1}^{3}+h_{2}^{3})}{3}$
$y_{G}=\frac{J_{x}}{A}=\frac{h_{1}-h_{2}}{2}$
$x$軸が図心上にある場合は、
$y_{G}=0$とおくと、$h_{1}=h_{2}$なので、
${\displaystyle I=\frac{b(2h_{1}^{3})}{3}=
=\frac{b(2\cdot(\frac{h}{2})^{3})}{3}=
\frac{bh^{3}}{12}}$
長方形の図心軸回りの断面2次モーメントが${\displaystyle \frac{bh^{3}}{12}}$
となることは、公式として覚えておくこと。
(重要)
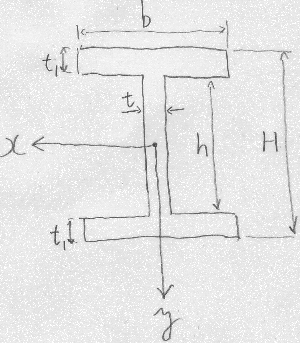 図のような2軸対称のI型断面の図心上に$x$軸があるとき、
$x$軸まわりの断面2次モーメントを求めよ。
図のような2軸対称のI型断面の図心上に$x$軸があるとき、
$x$軸まわりの断面2次モーメントを求めよ。
$I=\int_{A}y^{2}dA$
$=\int_{-\frac{H}{2}}^{-\frac{h}{2}}by^{2}dy
+\int_{-\frac{h}{2}}^{\frac{h}{2}}ty^{2}dy
+\int_{\frac{h}{2}}^{\frac{H}{2}}by^{2}dy$
$=[b\frac{y^{3}}{3}]_{-\frac{H}{2}}^{-\frac{h}{2}}
+[t\frac{y^{3}}{3}]_{-\frac{h}{2}}^{\frac{h}{2}}
+[b\frac{y^{3}}{3}]_{\frac{h}{2}}^{\frac{H}{2}}$
$=\frac{bH^{3}-(b-t)h^{3}}{12}$
$H=h+2t$を代入して$H$を消す場合:
$I=\frac{b(h+2t)^{3}-bh^{3}+th^{3}}{12}\\
=\frac{bh^{3}+6bh^{2}t+12bht^{2}+8bt^{3}-bh^{3}+th^{3}}{12}\\
=\frac{6bh^{2}t+12bht^{2}+8bt^{3}+th^{3}}{12}
$
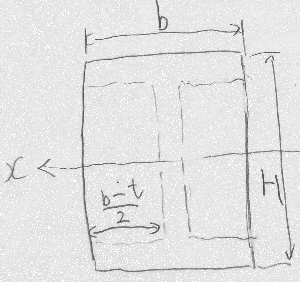 ついでに、$b \times h$の長方形に対する公式$\frac{bh^{3}}{12}$
を利用するなら、$b \times H$の大きい長方形の断面2次モーメントから
$\frac{b-t}{2}\times h$の小さい長方形2個ぶんの断面2次モーメントを
引くという便法によって求めた答えが、面積積分による答えと
一致することを確認せよ。具体的なやり方はここ。
ついでに、$b \times h$の長方形に対する公式$\frac{bh^{3}}{12}$
を利用するなら、$b \times H$の大きい長方形の断面2次モーメントから
$\frac{b-t}{2}\times h$の小さい長方形2個ぶんの断面2次モーメントを
引くという便法によって求めた答えが、面積積分による答えと
一致することを確認せよ。具体的なやり方はここ。
ちなみに、図形をいくつかの長方形に分解したときは、
それぞれの長方形の図心が同じ軸を通っていなければ、
そのまま足したり引いたりはできないので、
次項の公式($I_{X}=I_{x}+Y_{G}^{2}A$)を使う。
図心が同じ軸を通らない3つの長方形に分けた計算。
 一般に橋梁などの桁は、
コンクリートと鉄筋とか、コンクリートと鋼材とか、木材と鋼材とか、
異なる材料が組み合わされていることが多く、その場合、
断面形状も上下非対称になることが多いが、
仮に断面形状自体は上下対称だとしても、
中立軸が断面形状の図心軸とは一致しないことも多い。
そういう一般的な橋梁断面で、中立軸を求めたりといったことは、
恐らく、コンクリート構造とかの授業でもやるのではないかと思うが、
そういった場合に、図心から離れた軸回りの断面2次モーメントを求める必要が出てくる。
一般に橋梁などの桁は、
コンクリートと鉄筋とか、コンクリートと鋼材とか、木材と鋼材とか、
異なる材料が組み合わされていることが多く、その場合、
断面形状も上下非対称になることが多いが、
仮に断面形状自体は上下対称だとしても、
中立軸が断面形状の図心軸とは一致しないことも多い。
そういう一般的な橋梁断面で、中立軸を求めたりといったことは、
恐らく、コンクリート構造とかの授業でもやるのではないかと思うが、
そういった場合に、図心から離れた軸回りの断面2次モーメントを求める必要が出てくる。
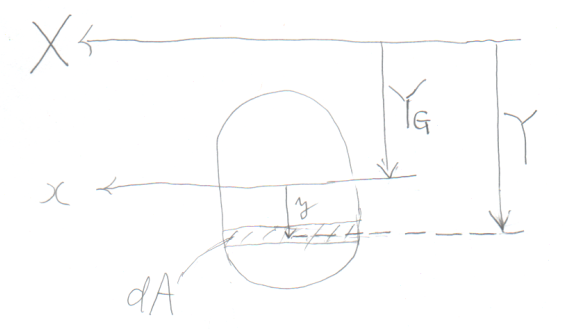
図のように、断面の図心軸が$x$の場合、
前回やったように、
図心軸回りの断面2次モーメント$I_{x}$は、
${\displaystyle I_{x}=\int_{A}y^{2}dA}$
で与えられる。
ではこの図心軸$x$から離れた$X$軸回りの断面2次モーメント$I_{X}$を求めてみよう。
$X$軸回りの断面2次モーメント$I_{X}$は、$X$軸の原点から$Y$座標を取ると、同様に
${\displaystyle I_{X}=\int_{A}Y^{2}dA}$
で与えられる。
さて、$X$軸から図心軸$x$までの距離が図のように$Y_{G}$で表されるとすると、
${\displaystyle I_{X}=\int_{A}Y^{2}dA}$
${\displaystyle =\int_{A}(Y_{G}+y)^{2}dA}$
${\displaystyle =\int_{A}(Y_{G}^{2}+2Y_{G}y+y^{2})dA}$
${\displaystyle =Y_{G}^{2}\int_{A}dA+2Y_{G}\int_{A}y dA+\int_{A}y^{2}dA}$
$=Y_{G}^{2}A+2Y_{G}J_{x}+I_{x}$
と変形できる。$x$軸は図心を通るから、断面1次モーメント$J_{x}=0$である。
つまり、
$I_{X}=I_{x}+Y_{G}^{2}A$
(重要)
となる。これは重要な公式であるので、覚えておくこと。
 同様に、図心軸から離れた軸回りの断面1次モーメントも求めてみよう。
同様に、図心軸から離れた軸回りの断面1次モーメントも求めてみよう。
図のように、断面の図心軸が$x$の場合、
前回やったように、
図心軸回りの断面1次モーメント$J_{x}$は、
${\displaystyle J_{x}=\int_{A}ydA}$
で与えられるが、図心を通る場合は、$J_{x}=0$である。
ではこの図心軸$x$から離れた$X$軸回りの断面1次モーメント$J_{X}$を求めてみよう。
このように図心を通らない軸回りの断面1次モーメントは0にはならないので、
なにかと必要になることもある。
$X$軸回りの断面1次モーメント$I_{X}$は、$X$軸の原点から$Y$座標を取ると、同様に
${\displaystyle J_{X}=\int_{A}YdA}$
で与えられる。
さて、$X$軸から図心軸$x$までの距離が図のように$Y_{G}$で表されるとすると、
${\displaystyle J_{X}=\int_{A}YdA}$
${\displaystyle =\int_{A}(Y_{G}+y)dA}$
${\displaystyle =Y_{G}\int_{A}dA+\int_{A}y dA}$
$=Y_{G}A+J_{x}$
と変形できる。$x$軸は図心を通るから、図心軸回りの断面1次モーメント$J_{x}=0$である。
つまり、
$J_{X}=Y_{G}A$
(重要)
となる。これも重要な公式であるので、覚えておくこと。
これを${\displaystyle Y_{G}=\frac{J_{X}}{A}}$と変形すれば、
前回やった図心の定義と同じことである。
図の片持梁では、$M=-Py_{1}$の負曲げが発生し、上縁に引張が生じるが、
2023/9/28まで、$M=Py_{1}$の曲げにより下端に引張が生じると書いていました。すいません。
前回、
$z$軸が図心を通る梁の断面の直応力は、次式で与えられることを学んだ。
${\displaystyle \sigma_{zz}(y,z)=
\frac{N(z)}{A}+\frac{M(z)}{I}y
}$
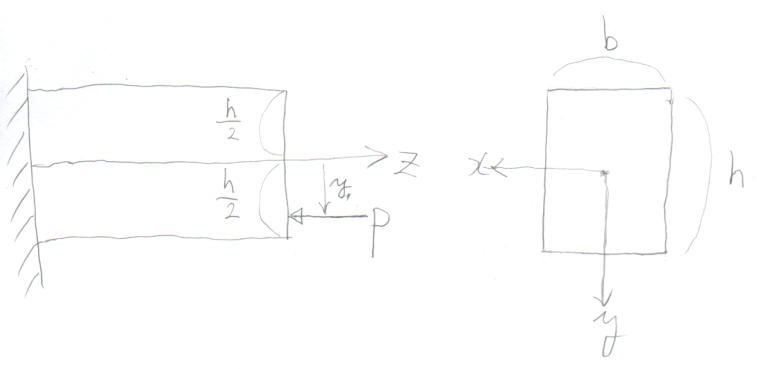 さて、図のような片持ち梁が、先端面で図心から$y_{1}$離れた点(の$y$軸上)に、
$P$の荷重を受ける場合の応力の状態を考えたい。
先端の荷重$P$が、ちょうど$z$軸上の図心位置に載荷されれば、
この片持ち梁には一様な圧縮力$N=-P$が発生すると考えられるが、
図心から$y_{1}$だけずれたところに載荷されると、$M=-Py_{1}$という
曲げモーメントも発生してしまう。
このように、梁や柱が断面の図心からずれたところに圧縮荷重を受けて、
曲げが発生してしまうような載荷状態のことを偏心載荷という。
コンクリートでは引張強度が小さく圧縮強度の$\frac{1}{10}$ぐらいなので、
コンクリートの圧縮部材では、引張の応力が発生しないようにするといった話は、
そのうちコンクリート構造とかの授業でやるのではと思う。
このように
断面に引張が発生しては困る部材では、
荷重が図心からどれくらいずれると、断面に引張が発生してしまうかという
ことを知りたい場合がある。
図のような偏心状態のときの断面の直応力は、
$N=-P$と$M=-Py_{1}$を上の式に代入すると、以下のように書ける。
さて、図のような片持ち梁が、先端面で図心から$y_{1}$離れた点(の$y$軸上)に、
$P$の荷重を受ける場合の応力の状態を考えたい。
先端の荷重$P$が、ちょうど$z$軸上の図心位置に載荷されれば、
この片持ち梁には一様な圧縮力$N=-P$が発生すると考えられるが、
図心から$y_{1}$だけずれたところに載荷されると、$M=-Py_{1}$という
曲げモーメントも発生してしまう。
このように、梁や柱が断面の図心からずれたところに圧縮荷重を受けて、
曲げが発生してしまうような載荷状態のことを偏心載荷という。
コンクリートでは引張強度が小さく圧縮強度の$\frac{1}{10}$ぐらいなので、
コンクリートの圧縮部材では、引張の応力が発生しないようにするといった話は、
そのうちコンクリート構造とかの授業でやるのではと思う。
このように
断面に引張が発生しては困る部材では、
荷重が図心からどれくらいずれると、断面に引張が発生してしまうかという
ことを知りたい場合がある。
図のような偏心状態のときの断面の直応力は、
$N=-P$と$M=-Py_{1}$を上の式に代入すると、以下のように書ける。
${\displaystyle \sigma_{zz}(y,z)=
-\frac{P}{A}
-\frac{Py_{1}}{I}y
}$
ここで、$-\frac{P}{A}<0$が一様な圧縮の成分で、
$-\frac{Py_{1}}{I}y>0$は、図心を通る三角形分布で
図心から上が正(引張)で図心から下が負(圧縮)となっている。
つまり、これらの足し算が正になり引張が発生する可能性が最も大きいのは、
引張の応力が最も大きくなる断面の上部(上縁つまり$y=-\frac{h}{2}$のとこ)ということになる。
つまり
断面の上縁の直応力は、以下のように書ける。
${\displaystyle \sigma_{zz}(y=-\frac{h}{2},z)=
-\frac{P}{A}
-\frac{Py_{1}}{I}\left(-\frac{h}{2}\right)
}$
さて、下縁の応力が引張にならないための条件は、この応力がプラスにならなければいいので、
${\displaystyle
-\frac{P}{A}
+\frac{Py_{1}}{I}\cdot\frac{h}{2}\le 0\\
}$
となる。
つまり、
${\displaystyle
\frac{Py_{1}}{I}\cdot\frac{h}{2}\le
\frac{P}{A}
}$
ということだ。
これを整理して$y_{1}$の最大値を求めると
${\displaystyle y_{1}\le \frac{2I}{hA}}$
となる。
長方形断面の場合について、
上の長方形断面の断面2次モーメントの公式
$\frac{bh^{3}}{12}$を使って、
この$y_{1}$の最大値$y_{1}^{最大}$を計算してみる。
${\displaystyle y_{1}^{最大}= \frac{2I}{hA}
=\frac{2\cdot\frac{bh^{3}}{12}}{h\cdot bh}
=\frac{h}{6}
}$
つまり、長方形断面の場合、図心から$\frac{h}{6}$以内のところに$P$が偏心載荷
されても、断面に引張応力は生じないということだ。
このように、引張応力が生じない最大の偏心量$y_{1}^{最大}$のことを
断面の核点と言う。
今、これは2次元で、梁が$x$軸回りの曲げを受ける場合を考えているが、
$y$軸回りの曲げを受ける場合の核点も同様に計算できる。
すると、断面の幅は$b$だから、$x$方向の核点は同様に$\frac{b}{6}$と求まる。
もちろん、梁は、$x$軸回りの曲げや$y$軸回りの曲げの他にも、
$xy$平面内の斜めの軸回りの曲げも受ける可能性がある。
その場合の核点も同様に計算はできるが、
断面2次モーメントとかの計算は難しくなる。
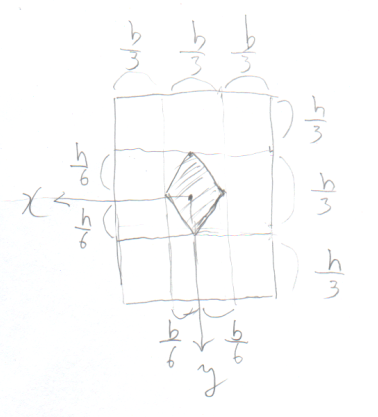 結果だけ示すと、$xy$平面内のすべての軸回りの曲げに対する核点を
プロットすると、図のようなひし形になる。
長方形断面では、このひし形の内部に偏心荷重$P$を受けても断面に引張が
生じないということになる。
この領域のことを断面の核と言う。
断面の核は、円形断面とか、$\text{I}$型断面とか、断面の形状に応じて求めることができる。
図書館で構造力学公式集とかを見れば、主要な断面の核が載っている。
構造力学(応用)の授業の中では、断面の核を使うことはないが、
コンクリート部材等では、重要な量なので、
何を表すものなのかということぐらいは理解しておくこと。
結果だけ示すと、$xy$平面内のすべての軸回りの曲げに対する核点を
プロットすると、図のようなひし形になる。
長方形断面では、このひし形の内部に偏心荷重$P$を受けても断面に引張が
生じないということになる。
この領域のことを断面の核と言う。
断面の核は、円形断面とか、$\text{I}$型断面とか、断面の形状に応じて求めることができる。
図書館で構造力学公式集とかを見れば、主要な断面の核が載っている。
構造力学(応用)の授業の中では、断面の核を使うことはないが、
コンクリート部材等では、重要な量なので、
何を表すものなのかということぐらいは理解しておくこと。
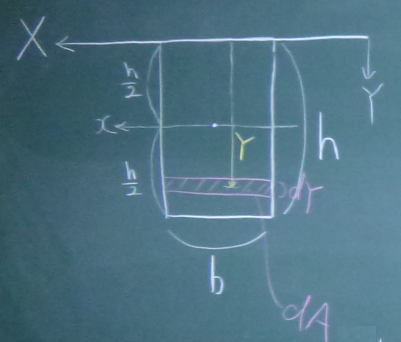 図のような長方形の$X$軸(てっぺんの辺)回りの
断面1次モーメント$J_{X}$と
断面2次モーメント$I_{X}$を求めよ。
定義通りに面積積分で求める方法も、
長方形の断面2次の公式や図心軸から離れた軸回りの公式を利用する方法も、
どちらでもできるように。
答えはここ。
図のような長方形の$X$軸(てっぺんの辺)回りの
断面1次モーメント$J_{X}$と
断面2次モーメント$I_{X}$を求めよ。
定義通りに面積積分で求める方法も、
長方形の断面2次の公式や図心軸から離れた軸回りの公式を利用する方法も、
どちらでもできるように。
答えはここ。
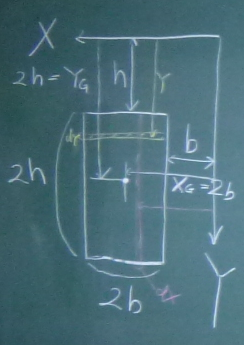 図のような長方形の$X$軸回りの断面2次モーメント$I_{X}$
と
$Y$軸回りの断面2次モーメント$I_{Y}$
を求めよ。
定義通りに面積積分で求める方法も、
長方形の断面2次の公式や図心軸から離れた軸回りの公式を利用する方法も、
どちらでもできるように。
答えはここ。
図のような長方形の$X$軸回りの断面2次モーメント$I_{X}$
と
$Y$軸回りの断面2次モーメント$I_{Y}$
を求めよ。
定義通りに面積積分で求める方法も、
長方形の断面2次の公式や図心軸から離れた軸回りの公式を利用する方法も、
どちらでもできるように。
答えはここ。
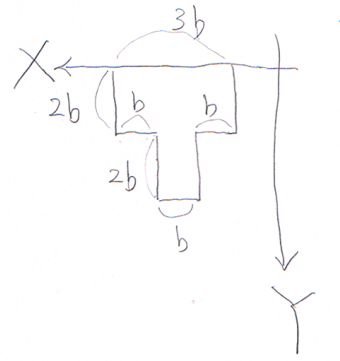 図のような2つの長方形を組み合わせた図形の$X$軸回りの
断面1次モーメント$J_{X}$を求め、この図形の図心の$Y$座標$Y_{G}$を求めよ。
次に、この図形の図心を通って水平な$x$軸回りの断面2次モーメント$I_{x}$を求めよ。
面積積分でも、公式でも、
どちらでも求められるように。
公式を使う場合、このように複数の長方形に分解できる図形の場合は、
それぞれの長方形についての量を足し算すればよい
(答え参照)。
答えはここ。
図のような2つの長方形を組み合わせた図形の$X$軸回りの
断面1次モーメント$J_{X}$を求め、この図形の図心の$Y$座標$Y_{G}$を求めよ。
次に、この図形の図心を通って水平な$x$軸回りの断面2次モーメント$I_{x}$を求めよ。
面積積分でも、公式でも、
どちらでも求められるように。
公式を使う場合、このように複数の長方形に分解できる図形の場合は、
それぞれの長方形についての量を足し算すればよい
(答え参照)。
答えはここ。
2022年度小テスト:
小テスト221116
2021年度小テスト:
問,
解答
2020年度小テスト:
問1, 問2, 問3,
解答
メモ: