構造力学Iオンライン授業用テキスト
第7回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
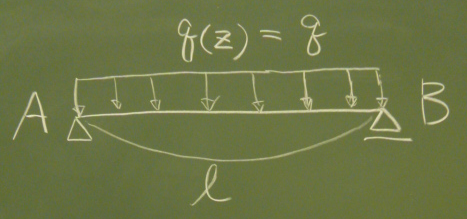前回までは、
梁の1点に集中的な外力（こういうのを集中荷重という）が
作用している問題ばかりを扱ってきた。
しかし、
実際の構造物で1点（面積が0の点）に、
に荷重が作用するということはまずあり得ない。
仮に面積が0の点にほんのちょっとでも点荷重が作用したら、
圧力は無限大になるから、瞬時に孔があいてしまうだろう。
というわけで、今回はもう少し現実に近い荷重を考える。
例えば、橋に載る車の荷重というのはタイヤが道路に接している
面に載荷されている。
あるいは、橋の上で車が渋滞してぎっしり車が並んでいる場合、
もちろん、1台1台の車の荷重は、そのタイヤの接地面から
橋にかかっているのだけど、
大まかに見るなら、橋の床版面（車が通るところ）に
平均化された車の荷重が一様に圧力のように載荷されていると
考えた方が便利かもしれない。
橋の床版面に一様に圧力のように荷重が載荷されている状態を
2次元の梁で考える場合、
奥行きは考えなくていいので、
梁の長さ当たりに荷重が一様に分布している状態ということになる。
このような荷重を等分布荷重という。
圧力の場合、面積あたりの力だから、単位はN/m$^2$のように
力/面積の次元になるけど、
2次元の等分布荷重の場合は、長さ当たりの力だから、
単位はN/mのように力/長さの次元になる。
もし、荷重が
例えば真ん中に近いほど大きくなるとか、
一様ではない場合、「等」をつけずに
分布荷重と言う。
分布荷重は$z$の関数として$q(z)$などの記号で表す。
等分布荷重の場合は、$z$の場所によらずに荷重は一定だから$q(z)=q$
など、定数で表す（関数$q(z)$を表す$q$と定数が同じ$q$というのが
紛らわしければ、$q_{0}$とかでもよい。
等分布荷重のときは、$q(z)$という表現はあまり使わないので、
定数を$q$としても特に問題はない）。
脱線(一応、読んでほしい)：
分布荷重の記号に$q$を使うと、
答案で色々と紛らわしいことが多い。
もう、だいぶ前から中学でも高校でも英語の筆記体を教えなくなったが、
困ったことに$q$のブロック体は、数字の9とほぼ同じ形で、
しかも発音も同じ「キュー」だ。
ブロック体の$q$と数字の9を混在させて書いた場合、
見ても聞いても、頭の中で読んでも実に紛らわしく、
計算間違いを誘発しやすい。
分布荷重の$q$は、筆記体で書くか、ブロック体で書く場合は、
せめて下を「し」みたいに右に反らせるとか、
下に横線を引くとか、
数字の9と
区別できるように工夫してほしい。
あと、筆記体の$q$が、筆記体の$g$と同じ人もいる。
もちろん、$g$も重力加速度で使われるから、
$q$と区別できる必要がある。あと、数字の8とも...
脱線（読まなくていい）：
構造力学で曲げモーメントの小テストとかを出すと、
$1\times 1=$と書いてくる答案がそれなりにある。
これを書いている時点で、まだ曲げモーメントの答案を回収していないから、
みなさんの答案がどうかはわからないが、
毎年、ほぼ一定数である。
最初に見たときは、どうして$1\times 1=$なのかわからなかったが、
まあ、答案の前後を見れば$M=$のことなのだが、
どうして$M$を$1\times 1$と書くのか、
なかなか不思議だった。
だんだんわかってきたのだが、どうやら中学の英語の授業で、
$M$の書き順を、一画ずつ、
｜＼／｜と書かされているようなのだ。
だから、急いで書くと、$1\times 1$となってしまうということらしい。
同じようなことは$N$とかにも当てはまる。
英語やラテン文字のアルファベットの正式の書き順というのは
あるのかもしれないが、
数学や工学の計算で、こうした書き順通りに書くのは、
書くのが遅くなって非効率なばかりか、
現に$1\times 1$のように見えたりして間違いを誘発する。
数学や工学の式の表記では、
文字の正式な書き順なんかよりも、
見やすく、早く正確に書け、他の文字と紛らわしくないことが
圧倒的に優先される。
$M$だの$N$だの一筆書きで書ける文字は、
式を書く場合には、
是非一筆書きで書くべきでは、と私は思う。
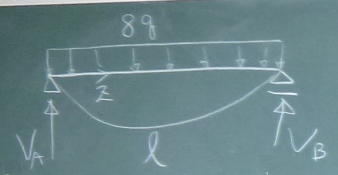
さて、では図のような等分布荷重$q$が、
単純梁の全長$\ell$に載荷されている問題を解いてみよう。
第5回で、集中荷重の作用する梁の場合分けについて、
集中荷重や反力の作用していない荷重のない領域では、
$S(z)$や$M(z)$は1つの式で書けるから、
集中荷重や反力の作用していない荷重のない領域ごとに場合分けすればよい
という話をした。
分布荷重が作用している領域がある場合、
もしその分布荷重が$q(z)$という1つの式で表せているなら、
その領域の$S(z)$や$M(z)$も1つの式で表せることになる。
この辺の話は
構造力学IIでやるが、
$M'(z)=S(z)$, $S'(z)=-q(z)$という関係があり、
$S(z)$も$M(z)$も、その領域の$q(z)$を積分したもので表せるので、
その領域で$q(z)$が1つの式で洗わせていれば、$S(z)$や$M(z)$も
1つの式で表せるということだ。
例えば、図のように梁の真ん中に分布荷重が載荷された領域があり、
その領域の分布荷重が例えば
$q(z)=a_{0}+a_{1}z+a_{2}z^{2}+a_{3}z^{3}+\cdots(a\le z \le b)$
みたいな1つの式で表されているなら、
左側の荷重のない領域$(0\le z\le a)$、
真ん中の荷重が$q(z)$で表される領域$(a\le z\le b)$、
右側の荷重のない領域$(b\le z\le \ell)$の3つの領域に場合分けして考えればよい。
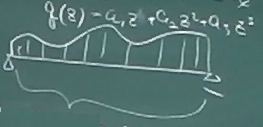図の梁のように、梁の左端から右端まで、
$q(z)=a_{0}+a_{1}z+a_{2}z^{2}+a_{3}z^{3}+\cdots\;\;\;\;\;(0\le z \le \ell)$
みたいな1つの式（別に多項式でなくてもいいが）で表される分布荷重が
作用しているなら、
$S(z)$や$M(z)$も1つの式で表されるので、
場合分けは不要である。
というわけで、
図のように等分布荷重$q$が、
単純梁の全長$\ell$に載荷されている問題の場合は、
梁の全長で、
$q(z)=q\;\;\;\;(0\le z \le \ell)$で1つの式で表されているから、
場合分けは不要である。
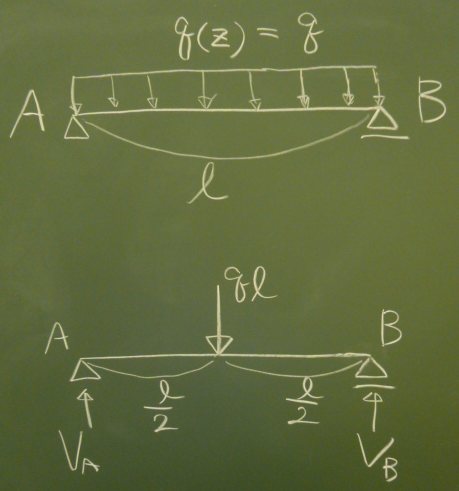まず反力を求めたいが、
分布荷重のまま力のつりあいを考えるのは
（できなくはないけど、モーメントを積分したりとか、ちょっとめんどくさいので）、
第1回でやった複数の外力を
1点に作用する力にまとめてしまう要領で、
この等分布荷重を1点に作用する1つの外力にまとめてしまいたい。
等分布荷重は、単位長さ当たりの荷重だから、
荷重の合計は梁の全長$\ell$をかけて$q\ell$となる。
これを荷重の重心位置に作用させれば、モーメントのつりあいは満たされる。
等分布荷重は、荷重の大きさを$\downarrow$の長さで表すと、
荷重が一定だから、図では長方形になる。
だから、長方形分布の荷重と言ってもいい
（ちなみに次回は三角形分布の荷重をやる）。
長方形分布の荷重であれば、長方形の重心の位置（要は真ん中）に
全荷重を集中荷重として載荷させれば、モーメントのつりあいは満たされる。
すると、図の下の梁のように梁の中央に$q\ell$の集中荷重が載荷された
問題の反力を求めれば、上の等分布荷重の反力を求めたのと同じことになる。
この梁の場合、左右対称だから、反力は
$V_{A}=V_{B}=\frac{q\ell}{2}$とすぐにわかるが、一応、力のつりあいから
求めるとすれば、以下のようになる。
$\Sigma\downarrow=-V_{A}+q\ell-V_{B}=0$
$\sum_{A}\circlearrowleft=-q\ell\cdot\frac{\ell}{2}+V_{B}\ell=0$
これらを解いて
$V_{A}=V_{B}=\frac{q\ell}{2}$
ただし、これはあくまで反力については、
この置き換えをしても置き換え前と同じになるということであって、
$S(z)$や$M(z)$については、置き換え前の梁と
置き換え後の梁では同じにはならない。
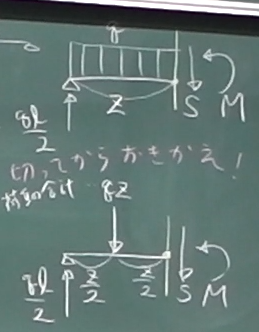次に、$S(z)$や$M(z)$を求めるには、
求めたい領域の任意の$z$で梁を切り離してやればよい。
場合分けはないので、どこで切ってもいいので、
適当な$z$で切る。
$S(z)$や$M(z)$を求めるために切るのは、
分布荷重の載荷されたもとの梁であって、
反力用に置き換えた梁ではないので注意すること。
切り離した2つのパーツのどちらかを取り出してつりあいを考えればいいが、
今回は左側のパーツを取り出す。
切断面には、
向きに注意して$S, M$を描き込む。
取り出したパーツについて力のつりあいを考えればいいのだが、
分布荷重があると考えにくい。
とういことで、
ここで、さっきと同じように等分布荷重を1点に作用する1つの荷重に
置き換えてやる。
つまり、
$S(z)$や$M(z)$を求めるときは、分布荷重の載荷されたもとの梁を
切ってから置き換えるということだ。
左側のピースの長さは、ある$z$で切ったから、
左端（原点）からある$z$までの距離だから$z$でよい。
つまり、このピースにかかる合計の荷重は、
$q$に長さ$z$をかけて$qz$ということになる。
この$qz$を長方形分布の重心の位置（つまり真ん中）つまり、
左端から$\frac{z}{2}$の位置に載荷すれば、
このピースのモーメントのつりあいは満たされる。
つまり、切断面の$S(z)$や$M(z)$に関しては、正しく求まる。
というわけで、図の下側の荷重を$qz$に置き換えた梁について、
力のつりあいを考える。
$\Sigma\downarrow=-\frac{q\ell}{2}+qz+S=0$
よって、$S(z)=\frac{q}{2}(\ell-2z)\;\;\;\;\;(0\le z \le \ell)$
$\sum_{z}\circlearrowleft=-\frac{q\ell}{2}z+qz\cdot\frac{z}{2}
+M=0$
よって、
$M(z)=\frac{q}{2}(\ell z-z^{2})\;\;\;\;\;(0\le z \le \ell)$
$M'(z)=S(z)$になることを確かめて検算する。
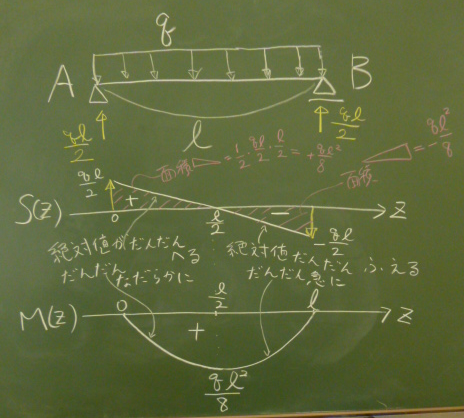それでは、第6回の要領で$S$図、$M$図を描いていく。
まず、式をそのままグラフにプロットして描く場合。
今回の$S(z)$は1次式で直線だから、
領域$(0\le z \le \ell)$の両端の値を求めて直線で結べばよい。
$S(0)=\frac{q}{2}(\ell-2\cdot 0)=\frac{q\ell}{2}$,
$S(\ell)=\frac{q}{2}(\ell-2\ell)=-\frac{q\ell}{2}$
だから、
$(0, \frac{q\ell}{2})$と
$(\ell, -\frac{q\ell}{2})$を直線で結ぶ。
すると、途中で$z$軸と交わるから、その交点を求める。
まあ、左右対称だから真ん中で交わるはずだが、
$0=S(z)=\frac{q}{2}(\ell-2z)$を解くと、$z=\frac{\ell}{2}$
となる。だから、真ん中の交点のところに$\frac{\ell}{2}$と書く。
次に曲げモーメント。
今回の$M(z)$は2次式だから、曲線のグラフになるから、ちょっと
やっかいだ。
まずは、領域の両端の値を求めておこう。
まあ、両端ともヒンジだから ともに0になるはずだが。
$M(0)=\frac{q}{2}(\ell\cdot 0 -0^{2})=0$
$M(\ell)=\frac{q}{2}(\ell\cdot \ell -\ell^{2})=0$
確かに両端では0だ。
こういう曲線のグラフを描くとき、 高校の数学では、1階微分$M'(z)$と2階微分$M''(z)$を求め、 それらの正負を調べ、 増減表を書いて上に凸とか下に凸といった判定をしながら グラフを描いたんじゃないかと思う。 でも、そういうことをするとめんどくさいし、 $S$図や$M$図は上が正だったり、下が正だったりするから、 「上に凸」というのは、座標の正方向に凸なのか、 書いている上方向に凸なのか、非常に混乱する。 だから、$M$図を描くときは、 $S(z)=M'(z)$であることを利用して、 $S$図を見ながら、以下の手順で描いてほしい。
このやり方を覚えれば、$S$図を見さえすれば、 $S$図や$M$図の上が正でも下が正でも、 自動的に$M$図が描け、上に凸、下に凸も適切に反映される。 つまり、 M(z)の傾きがだんだんなだらかになるのか、だんだん急になるのかを、 S(z)の絶対値がだんだん減っているのか、だんだん増えているのかで 判定しさえすれば、自動的に下に凸か上に凸かも描けるのだ。
今回の例で、上のやり方を適用してみる。
$M(z)$は、真ん中の$z=\frac{\ell}{2}$で最大値を取ることは、 ここで$S(z)$が0となることからもわかるが、 $S(z)$や$M(z)$が極地をとる場合は、その値を（$q$や$\ell$を用いて） 記入すること。 今回は、 $M(\frac{\ell}{2})=\frac{q}{2}(\ell\cdot\frac{\ell}{2}-(\frac{\ell}{2})^{2}) =\frac{q\ell^{2}}{8}$となる。
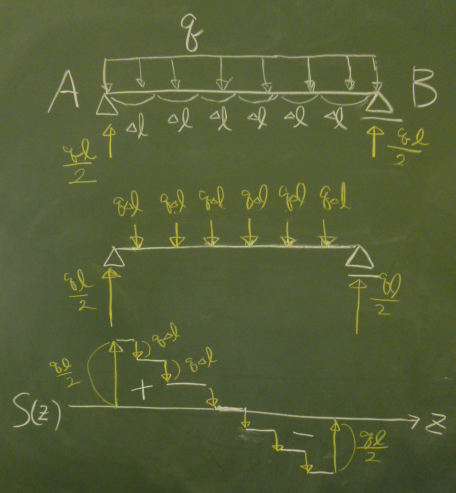第6回で、
$S$図は反力や外力をそのままプロットすれば描けると言った。
では、このような等分布荷重の場合はそうやって描けるだろうか。
等分布荷重を$n$個の集中荷重に置き換えれば、
それらをプロットしていくことで、$S$図が描けることになるのではないだろうか。
$q\ell$を$n$個に分けたのであれば、
$\Delta\ell=\frac{\ell}{n}$の領域に作用する等分布荷重は、
$q\Delta\ell$の集中荷重に置き換えられる。
そうすると、
左端で反力$\frac{q\ell}{2}$だけ持ち上がって、
そこから$q\Delta\ell$ずつ階段状に下がっていって、
$n$個ぶん下がるとちょうど$q\ell$ぶん下がったことになるから、
$\frac{q\ell}{2}-q\ell=-\frac{q\ell}{2}$まで下がっていることになる。
最後に右端の反力$\frac{q\ell}{2}$だけ上に上がると$0$まで戻る。
これだと階段状の近似でしかないが、
$n$を無限大まで増やしていけば、
このイメージで描ける。
上の$M$図と同様に、この階段がだんだんなだらかになるのか、
だんだん急になるのか、傾き一定なのかという問題はあるが、
まあ、$S'(z)=-q(z)$の関係があるから、
分布荷重$q(z)$は$S(z)$の傾きにマイナスをつけたものだ。
つまり、$q(z)=q=$一定なら、
$S(z)$の傾きは一定で、直線で表される。
だから、まず、左端で
反力$\frac{q\ell}{2}$だけ持ち上がって、
$q(z)=q=$一定だから、
そこから傾き一定でまっすぐ下がり続け、
どこまで下がるかというと、分布荷重の合計は$q\ell$だから、
$\frac{q\ell}{2}$から$q\ell$だけ下がって
右端では
$-\frac{q\ell}{2}$になる。
そこから右端の反力$\frac{q\ell}{2}$だけ上がって$0$に戻る。
なお、$M(z)$は$S(z)$を積分したものだから、
$S$図の左半分の三角形の面積
$\frac{1}{2}\cdot\frac{q\ell}{2}\cdot\frac{\ell}{2}=+\frac{q\ell^{2}}{8}$
は、中央の$M(\frac{\ell}{2})$の値と一致する。
そこから右半分の$S$図の三角形の面積は
$-\frac{q\ell^{2}}{8}$だから、
中央の値に足すとちょうど右端で$0$に戻る。
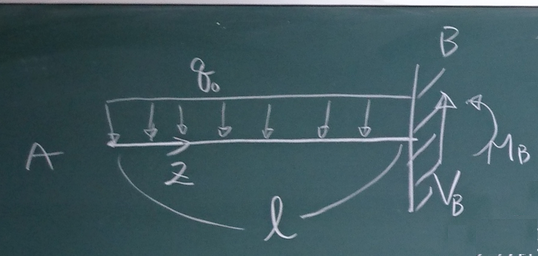
以下の梁について、$S(z)$, $M(z)$を求め、
$S$図（上が正）、$M$図（下が正）を描け。
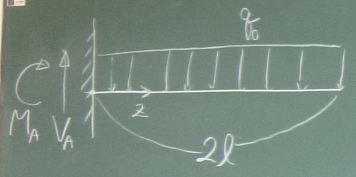答えは、ここ
答えは、ここ
答えは、ここ
2020年度小テスト： 問1, 問2, 問3, 問4, 解答
メモ:
