
構造力学(基礎)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
前回は、
部材力と呼ばれるトラスの内力の求め方を学んだ。
両端がヒンジになっている
理想的なトラス部材には軸力しか
内力が生じないので、話が簡単だった。
しかし、部材どうしがしっかり固定されている棒部材の場合、
まあ、部材が十分に細長ければ、トラスに近い挙動を示すとは言え、
厳密には、
軸力以外の力も作用する。
内力として、
軸力以外の力も作用する棒部材を、ひとまずここで
「
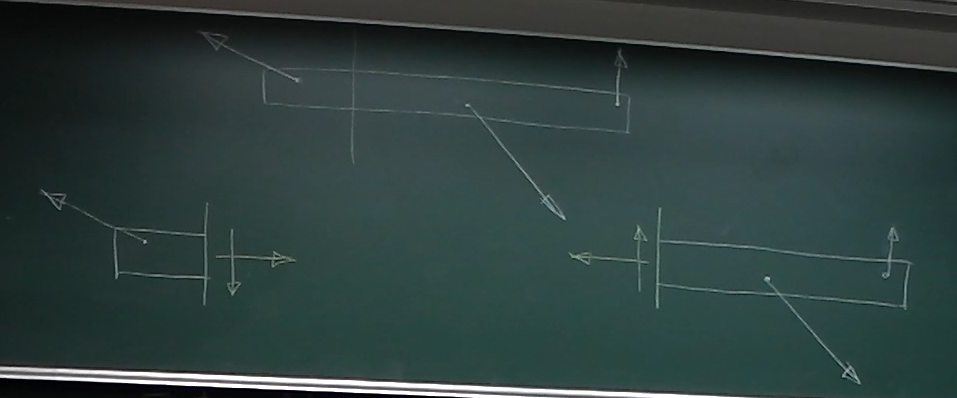 以下に梁(はり)の内力を定義する。
今、この棒にいくつかの外力が作用して空中でつりあっているとする。
この棒の適当なところを棒の軸線に直角な面で切り、棒を二つのパーツに
切り離してみる。
まずは切り離された左側のパーツについて考えてみる。
棒は切り離される前は、外力とそれによるモーメントの合計がゼロになって
つりあっていたが、切り離されてしまうと、
切り離されたパーツに作用する外力だけではつりあいが成り立たなくなってしまう。
そこで、切り離されたことによってできた切断面に、
切り離されたパーツだけでつりあうような力が作用していると考えてやる。
切り離されたパーツがつりあいを満たすように切断面に作用させる力は、
任意の与え方ができるが、扱いやすくするため、
切断面の重心に作用する次の3つの力として与えることにする。
以下に梁(はり)の内力を定義する。
今、この棒にいくつかの外力が作用して空中でつりあっているとする。
この棒の適当なところを棒の軸線に直角な面で切り、棒を二つのパーツに
切り離してみる。
まずは切り離された左側のパーツについて考えてみる。
棒は切り離される前は、外力とそれによるモーメントの合計がゼロになって
つりあっていたが、切り離されてしまうと、
切り離されたパーツに作用する外力だけではつりあいが成り立たなくなってしまう。
そこで、切り離されたことによってできた切断面に、
切り離されたパーツだけでつりあうような力が作用していると考えてやる。
切り離されたパーツがつりあいを満たすように切断面に作用させる力は、
任意の与え方ができるが、扱いやすくするため、
切断面の重心に作用する次の3つの力として与えることにする。
構造力学(応用)でやるが、
実際には、梁の切断面には「応力」という内力が分布しているが、
梁モデルでは、これらの内力を
1点に作用する以下の3つの力にまとめて扱うということ。
 軸力$N$: 切断面に垂直な(軸方向の)1つの力
軸力$N$: 切断面に垂直な(軸方向の)1つの力
せん断力$S$: 切断面に平行な1つの力
曲げモーメント$M$: 切断面に作用する1つのモーメント
NとかSといった記号は、あまり本質ではないし、他の記号を
使っているテキストもある。
軸力は英語では、axial forceとかだが、
Aは断面積によく使うから、normal force(法線力、面に垂直な力)の
Nかな。
せん断力は英語では、shear forceとかshearing forceなので、S.
日本語でも sendan だから、まあわかりやすいだろう。
せん断力にQを使う人も多いが、shearやsendanを連想しやすいSを
使っておこう。
MはmomentのMだが、日本語の「曲げ」も連想しやすいので、
Mでいいだろう。ちなみに「曲げモーメント」は英語では、
bending momentなので、Bを使う場合もある。
これらの力は、物体を仮想的に切断したことにより、
(つりあいを満たすために)仮想切断面に作用する力という意味で
「内力」という。
梁部材に限らずこのように物体の内部に作用していると考える力は内力であるが、
梁部材に限定した場合、その断面に作用する上記の3つの力は「断面力」ともいう。
さて、ここまでは切り離された左側のパーツについて述べてきたが、
切り離された右側のパーツの切断面についても、
右側のパーツが外力とつりあうように同様に断面力が作用する。
左側のパーツの右端の切断面に作用する断面力と
右側のパーツの左端の切断面に作用する断面力とは、
作用・反作用の関係により
互いに向きが反対で大きさが等しい力となる。
例えば、左側のパーツの右端の切断面に作用する軸力と
右側のパーツの左端の切断面に作用する軸力は向きが逆で大きさが等しいので、
切断面どうしをくっつけると、
切断面に作用する軸方向の力の合計はゼロになり、
切断面に外力としては軸方向の力は作用していないことになる。
せん断力や曲げモーメントも同様で、切断面どうしをくっつけてやると、
内力の合計はゼロになり、くっついた切断面には、切り離される前の状態と
同じようになにも外力は作用していないことになる。
構造力学で使われる 断面力の正の向きは座標の正の向きではないので、注意が必要である。 切断面における作用・反作用の関係が分かりやすいように、 左側の切断面と右側の切断面とでは正の向きを逆に定義している。 このように定義した方が、「向きは同じだけど符号が逆」と定義されるよりも 視覚的には考えやすい。但し、 コンピューターで大量の変位自由度を扱う マトリクス法などの有限要素解析の「節点力」においては、 力の向きと座標の向きが一致していた方が便利なので、 「向きは同じだけど符号が逆」の扱いになる。 軸力$N$の正の向きは梁が引張を受ける向きである。 せん断力$S$の正の向きは、左側パーツの右端の切断面では下向きが正、 右側パーツの左端の切断面では上向きが正である。 曲げモーメントの正の向きは、梁の下側が引張側となる向きが正である。
 これらの断面力の正の向きと具体的な変形の向きとの対応は、
切断位置に微小要素を介して、3つのパーツに切り分けて考えると
わかりやすいかも知れない。
真ん中の微小パーツは、正の軸力を受けると左右に引っ張られて伸び、
正のせん断力を受けると左の面は持ち上げられて右の面は持ち下げられて
右下がりにせん断変形し、
正の曲げモーメントを受けると上側が圧縮され、下側が引張られる。
ちなみに「せん断」というのは、漢字では「剪断」で、
ハサミなどで断ち切ることだが、
向かい合う二面を互いに反対方向にずらすような力や変形を表す。
これらの断面力の正の向きと具体的な変形の向きとの対応は、
切断位置に微小要素を介して、3つのパーツに切り分けて考えると
わかりやすいかも知れない。
真ん中の微小パーツは、正の軸力を受けると左右に引っ張られて伸び、
正のせん断力を受けると左の面は持ち上げられて右の面は持ち下げられて
右下がりにせん断変形し、
正の曲げモーメントを受けると上側が圧縮され、下側が引張られる。
ちなみに「せん断」というのは、漢字では「剪断」で、
ハサミなどで断ち切ることだが、
向かい合う二面を互いに反対方向にずらすような力や変形を表す。
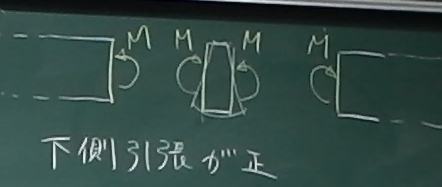 つまり、真ん中の微小部分について、以下のように覚えておけばよい。
つまり、真ん中の微小部分について、以下のように覚えておけばよい。
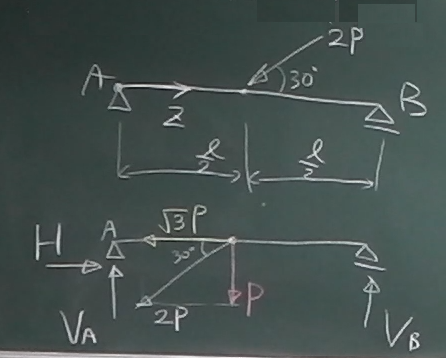 図のような簡単な例題について、
梁の軸上の任意点の軸力、せん断力、曲げモーメントを求めて、
それらを図示するまでの基本的な手順をやってみる。
図のような簡単な例題について、
梁の軸上の任意点の軸力、せん断力、曲げモーメントを求めて、
それらを図示するまでの基本的な手順をやってみる。
図のように一端がヒンジ支承に支持され、
他端がローラー支承に支持されている梁の場合、
反力が3個で静定構造だから、
力のつりあいだけで反力が求まる。
このような、ヒンジ支承とローラー支承で支持された梁のことを
単純支持梁とか単純梁と言う。
梁の基礎的な問題の場合は、外力として鉛直荷重しか作用しない問題が多いが、
斜め方向の荷重が作用している場合は、
作用点に作用する鉛直方向の力と水平方向の力とに分解してやる。
図のように矢印の先端を作用点にくっつけて描かれると、
分解するときにわかりにくいので、
作用点から矢印が突き出るように描き直してから分解するとわかりやすい。
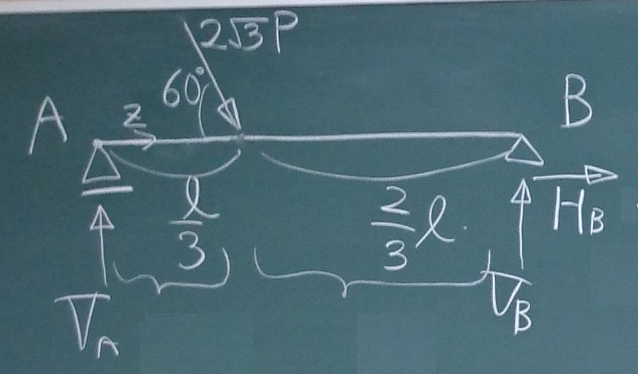
支承のところで説明したそれぞれの
支承の種類と反力の正の向きに注意して、
支点Aに作用する鉛直反力を$V_{A}$, 水平反力を$H_{A}$,
支点Bに作用する鉛直反力を$V_{B}$とする。
力のつりあいから
鉛直方向のつりあい(下向き正):$\Sigma\downarrow=(-V_{A})+(+P)+(-V_{B})=0$
水平方向のつりあい(右向き正):$\Sigma\rightarrow=(+H_{A})+(-\sqrt{3}P)=0$
支点Aまわりのモーメントのつりあい(左回り正):
$\sum_{A}\circlearrowleft=
-P\cdot \frac{\ell}{2}+V_{B}\cdot \ell=0$
の3式がなりたつ。未知数は$V_{A}, V_{B}, H_{A}$の3個だから
式が3個あれば解くことができて、
$H_{A}=\sqrt{3}P $
$V_{B}=\frac{P}{2}$
$V_{A}=\frac{P}{2}$
と求まる。
任意点の断面力を座標の関数として求めるには、座標を決めなければならない。
梁の左端の点を原点とし、軸に沿って右向きに$z$軸を、
下向きに$y$軸を取る($y,z$軸をこの向きに取る理由については
力の分解・整理参照)。
特に断りがない限り、梁の左端に原点を取るのが暗黙の了解である。
断面力を求めるというのは、
断面力$N$, $S$, $M$を$z$の関数として表すということだ。
つまり、断面力は厳密には、
$N(z)$, $S(z)$, $M(z)$のように$z$の関数として
書くのが正確な表記だが、
いちいち書くとめんどくさいので、
図の中とか計算途中では$(z)$は省略して、$N$, $S$, $M$と書くことにする。
断面力を求めるには、
梁を適当な断面で切断して、断面力が見えるようにする必要があるが、
どこで切断すべきかは、
$N(z)$, $S(z)$, $M(z)$のそれぞれを1つの式で表せる梁の領域($z$の範囲)が、
どこからどこまでかということを考えて、
場合分けする必要がある。
梁の途中にいくつかの集中外力(1点に作用する外力)がある場合、
一般に、集中外力や反力の作用していない領域では、
$N(z)$, $S(z)$, $M(z)$のそれぞれは1つの式で表せる
(別の領域では違う式になる)。
例えば、右の梁のように、途中に2つの集中外力が作用している場合には、
それら集中外力や両端の反力の作用していない間の部分
( でくくった
3箇所)では、
$N(z)$, $S(z)$, $M(z)$のそれぞれは1つの式で表せる。
つまり、3箇所の
でくくった
3箇所)では、
$N(z)$, $S(z)$, $M(z)$のそれぞれは1つの式で表せる。
つまり、3箇所の
 でくくった部分について、
場合分けをすればよい。
まず
左側の
でくくった部分について、
場合分けをすればよい。
まず
左側の
 でくくった領域について、
$N(z)$, $S(z)$, $M(z)$を求めたければ、
その領域のどこか(任意の$z$)で、断面を切断して、
切り離した左右のピースのどちらかについて力のつりあいを考えればいいし、
真ん中の
でくくった領域について、
$N(z)$, $S(z)$, $M(z)$を求めたければ、
その領域のどこか(任意の$z$)で、断面を切断して、
切り離した左右のピースのどちらかについて力のつりあいを考えればいいし、
真ん中の
 でくくった領域について、
$N(z)$, $S(z)$, $M(z)$を求めたければ、
その領域のどこか(任意の$z$)で、断面を切断して、
切り離した左右のピースのどちらかについて力のつりあいを考えればいいし、
右側の
でくくった領域について、
$N(z)$, $S(z)$, $M(z)$を求めたければ、
その領域のどこか(任意の$z$)で、断面を切断して、
切り離した左右のピースのどちらかについて力のつりあいを考えればいいし、
右側の
 でくくった領域について、
$N(z)$, $S(z)$, $M(z)$を求めたければ、
その領域のどこか(任意の$z$)で、断面を切断して、
切り離した左右のピースのどちらかについて力のつりあいを考えればいいという
ことになる。
でくくった領域について、
$N(z)$, $S(z)$, $M(z)$を求めたければ、
その領域のどこか(任意の$z$)で、断面を切断して、
切り離した左右のピースのどちらかについて力のつりあいを考えればいいという
ことになる。
 さて、今回の右の図の梁の場合、集中外力は真ん中に1つだけだから、
集中外力の左側(この例では$0\le z \le\frac{\ell}{2}$)の部分と
右側(この例では$\frac{\ell}{2}\le z\le \ell$)の部分
では、
$N(z)$, $S(z)$, $M(z)$のそれぞれは1つの式で表せる。
さて、今回の右の図の梁の場合、集中外力は真ん中に1つだけだから、
集中外力の左側(この例では$0\le z \le\frac{\ell}{2}$)の部分と
右側(この例では$\frac{\ell}{2}\le z\le \ell$)の部分
では、
$N(z)$, $S(z)$, $M(z)$のそれぞれは1つの式で表せる。
領域の境界について
:
$\le$は$=$つきの不等号のことだが、
$=$を二重線で書きたい人は、それでもいい。
式を書くツールの関係もあるが、私はめんどくさいんで手書きのときも1本
にしている。
左側の領域を$0 \le z \le \frac{\ell}{2}$で表したら、
$z=\frac{\ell}{2}$までを含んでいるから、
右側の領域は$z=\frac{\ell}{2}$を除いて、
$\frac{\ell}{2}< z \le\ell$
とすべきだという
意見もあるかもしれない。
実は、この辺の扱いは、構造力学ではそれほど厳密ではなく、
テキストによっても様々な表記があるだろう。
構造力学では、それぞれの領域の境界で
$N$, $S$, $M$を求めなくてはいけないが、
右側の領域を
$\frac{\ell}{2}< z \le\ell$
としてしまうと、左端の値を求める際に
$S(\frac{\ell}{2})$など、$z=\frac{\ell}{2}$を
代入するときに気持ち悪いので、最近は、
私は全ての領域の境界に$=$も入れている。
昔は、どちらも$=$を入れてなかった。
そういう意味では、断面力の領域の書き方は$\le$でも$<$でもどちらでもいい。
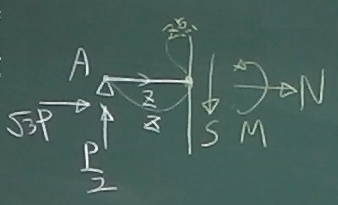 まず、外力の作用点よりも左側の$0\le z \le \frac{\ell}{2}$の
領域について、
断面力を求める。
$0\le z \le \frac{\ell}{2}$の任意点で梁を左右のピースに切り分け、
どちらか簡単そうなピースを取り出してつりあいを考える。
今回は左側のピースを取り出して考えることにする
(もちろん、右側のピースを取り出して考えても求まる断面力は
同じである)。
断面力の正の向きに注意しながら、
切断面に軸力$N$, せん断力$S$, 曲げモーメント$M$を書き入れ、
力のつりあいを考える。
まず、外力の作用点よりも左側の$0\le z \le \frac{\ell}{2}$の
領域について、
断面力を求める。
$0\le z \le \frac{\ell}{2}$の任意点で梁を左右のピースに切り分け、
どちらか簡単そうなピースを取り出してつりあいを考える。
今回は左側のピースを取り出して考えることにする
(もちろん、右側のピースを取り出して考えても求まる断面力は
同じである)。
断面力の正の向きに注意しながら、
切断面に軸力$N$, せん断力$S$, 曲げモーメント$M$を書き入れ、
力のつりあいを考える。
鉛直方向のつりあい(下向き正):$\Sigma\downarrow= (-\frac{P}{2})+(+S)=0$
水平方向のつりあい(右向き正): $\Sigma\rightarrow=(+\sqrt{3}P)+(+N)=0$
切断点($z$点)まわりのモーメントのつりあい(左回り正):
$\sum_{z}\circlearrowleft=
-\frac{P}{2}z+M=0$
モーメントのつりあいは、支点まわりで考えても切断点まわりで考えても
どこで考えても構わないが、
切断点の$S$などの未知数がモーメントを作るのを避けたければ、
切断点まわりのモーメントのつりあいを考えるのがおすすめである。
切断点は、任意の$z$の点だから、この点を今後$z$点と呼ぶことにする。
支点Aの反力$\frac{P}{2}$が$z$点まわりにつくるモーメントの
腕の長さは、支点Aから、切断点$z$までの距離だが、
$z$軸は梁の左端(この場合は支点A)を原点とするので、
支点Aから切断点(任意の$z$)までの距離は、
$z$で表される。
座標軸の$z$と、その具体的な任意の座標(例えば$z_{1}$とか)を
区別して、切断点を$z=z_{1}$とかで表した方がすっきりするという人は、
それでもいいが、最終的に、断面力を$z$の関数で表すので、
いちいち区別しないで$z$を距離に用いる。
それから、切断面に作用する曲げモーメント$M$は、
切断点($z$点)まわりのモーメントのつりあいを考えている場合も無視できない。
未知数が$N$, $S$, $M$の3個で式が3個だから解くことができて、
$
\begin{array}{ll}
S=\frac{P}{2} & \;\;\;\;(0\le z \le \frac{\ell}{2})\\
N=-\sqrt{3}P & \;\;\;\;(0\le z \le \frac{\ell}{2})\\
M=\frac{P}{2}z & \;\;\;\;(0\le z \le \frac{\ell}{2})
\end{array}
$
と求まる。
念のため、点Aまわりにモーメントのつりあいを考えた場合は、
$\sum_{A}\circlearrowleft=-Sz+M=0$
となるが、モーメント$M$は、どこに作用していたとしても、そのまま足せばよい。
モーメントは既にモーメントの次元なので、これに腕の長さ$z$をかけたりしないように。
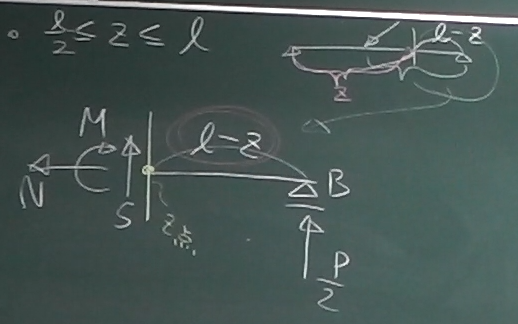 次に、外力の作用点よりも右側の$\frac{\ell}{2} \le z \le \ell$の
領域について、
断面力を求める。
次に、外力の作用点よりも右側の$\frac{\ell}{2} \le z \le \ell$の
領域について、
断面力を求める。
$\frac{\ell}{2} \le z \le \ell$の
任意点で梁を左右に切り分け、
どちらか簡単そうなピースを取り出してつりあいを考える。
今回は右側のピースを取り出して考えることにする
(もちろん、左側のピースを取り出して考えても求まる断面力は
同じである)。
断面力の正の向きに注意しながら、
切断面に軸力$N$, せん断力$S$, 曲げモーメント$M$を書き入れ、
力のつりあいを考える。
右のピースの断面力は、左のピースの断面力とくっつけたときに、
作用・反作用でプラマイゼロになる逆向きになっていないといけない。
鉛直方向のつりあい(下向き正):$\Sigma\downarrow= (-S)+(-\frac{P}{2})=0$
水平方向のつりあい(右向き正): $\Sigma\rightarrow=(-N)=0$
切断点($z$点)まわりのモーメントのつりあい(左回り正):
$\sum_{z}\circlearrowleft=
-M+\frac{P}{2}(\ell-z)=0$
ここで、やや迷うのは、支点Bの反力$\frac{P}{2}$が、
切断点($z$点)まわりにつくるモーメントの腕の長さである。
$z$軸の原点(支点A)から切断点までの長さが$z$だから、
切断点から支点Bまでの長さは、$\ell-z$となる。
未知数が$N$, $S$, $M$の3個で式が3個だから解くことができて、
$
\begin{array}{ll}
S=-\frac{P}{2} & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)\\
N=0 & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)\\
M=\frac{P}{2}(\ell-z) & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)
\end{array}
$
と求まる。以上の
$0\le z \le \frac{\ell}{2}$の領域と
$\frac{\ell}{2}\le z \le \ell$の領域をまとめて書けば、以下のようになる。
$
\ \\
N(z)=
\begin{cases}
-\sqrt{3}P & \;\;\;\;(0\le z \le \frac{\ell}{2})\\
0 & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)
\end{cases}
\ \\
$
$
S(z)=
\begin{cases}
\frac{P}{2} & \;\;\;\;(0\le z \le \frac{\ell}{2})\\
-\frac{P}{2} & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)\\
\end{cases}
\ \\
$
$
M(z)=
\begin{cases}
\frac{P}{2}z & \;\;\;\;(0\le z \le \frac{\ell}{2}) \\
\frac{P}{2}(\ell-z) & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)
\end{cases}
\ \\
$
これらをグラフにしたものをN-図、S-図、M-図などと言うが、
その描き方は次回やる。
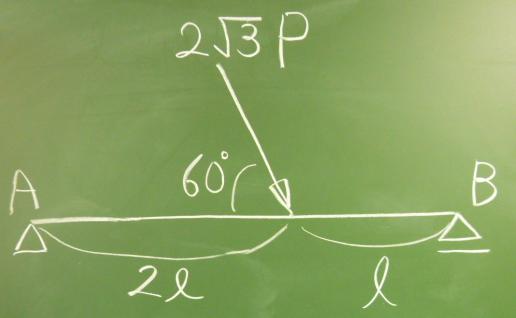 以下の梁について、軸力$N(z)$, せん断力$S(z)$, 曲げモーメント$M(z)$を
$z$の関数として求めよ。
特に断りがない限り、$z$軸は左端を原点とし、梁に沿って右向きに取る。
梁の長さは、$\ell$とは限らない。
この梁は、全体で$0\le z \le 3\ell$の領域があるので、
それをどう場合分けすればいいか。
答えは、ここ
以下の梁について、軸力$N(z)$, せん断力$S(z)$, 曲げモーメント$M(z)$を
$z$の関数として求めよ。
特に断りがない限り、$z$軸は左端を原点とし、梁に沿って右向きに取る。
梁の長さは、$\ell$とは限らない。
この梁は、全体で$0\le z \le 3\ell$の領域があるので、
それをどう場合分けすればいいか。
答えは、ここ
 答えは、ここ
答えは、ここ
2024年度小テスト:
小テスト240524
2020年度小テスト:
問題,
解答
メモ: