マトリクス構造解析オンライン授業用テキスト
第1回オンライン授業
小さい字は補足説明なので、読み飛ばしてもいいです。
1次元のばねの剛性方程式を導いてみる。
1次元なので、軸は$z$軸だけを考える。
空中というか（1次元の世界では$z$軸しかないので）$z$軸上に
長さ$\ell$, ばね定数$k$の
ばねが浮いているとする。
今は、1つのばねしか考えていないのだが、
ひとまず、この1つのばねを1要素のばね要素と考える
（そのうち長いばねで、途中から折れ曲がってたり、ばね定数が変わってたり
する場合は、複数のばね要素で解くことになる）。
梁の軸を$z$にした構造力学に合わせて、
ばね要素の軸を$z$軸とし、右向きに$z$軸を取る。
梁やばね要素の軸を$z$軸にする理由は、3次元に拡張した場合に、
断面の$x$方向、$y$方向を対等に扱い、
$z$を特殊な軸としておきたいからだが、
ばね要素の軸を$x$としているテキストは多いので、
他のテキストのマトリクスを参照する場合は、注意が必要となる。
1次元のばね要素では、$z$でも$x$でも違いはないが、
2次元の梁要素の場合、$yz$座標系と$xy$座標系とでは、
右手系のベクトルの並べ順がかわってくるので、
マトリクスの並びが変わってくる
（そのときに、またその話をする）。
ばね要素は、軸力だけが作用し、軸方向だけに伸び縮みする要素なので、 トラス要素と言うこともある。 つまり、$k=\frac{EA}{\ell}$の棒 ($E$はヤング率で$A$は断面積) として描いてもいいのだけど、 ばねで描いた方が最初はわかりやすいので、最初はばね定数$k$で話を進める。
要素の両端は節点と言い、複数の要素がある場合は、節点が隣の要素とつながることになる。 1つのばね要素は左右に1つずつの合計2つの節点がある。 この節点に、左側を節点1, 右側を節点2と名前をつける。 節点1と節点2に作用する力をそれぞれ節点力$N_{1}$, 節点力$N_{2}$とする。 節点力というのは、節点に作用する力で、 例えば、この図のように空中に浮いているばねに作用している場合は、 外力と考えてもいい。 だから、節点外力と言う場合もある。 しかし、後でやるが、反力や断面力を求める場合には、 節点力は、外力ではなく、内力を表す場合もあるので、 混乱を避けるため、節点力という表現を用いておく。 節点力はすべて、座標$z$の正の方向を正とする。 これは、構造力学の軸力（引張が正）の向きとは違うので注意が必要である。 マトリクス構造解析は、 コンピューターで解きやすいことに特化しているため、 節点力の向きをすべて同じ向きに定義して、 重ね合わせなどコンピューター内での処理がしやすいようにしている。 だから、この図を見ると、$N_{1}$も$N_{2}$も右向きだったら、 ばね要素は右向きに吹っ飛ぶのでは、と思うかもしれないが、 これが空中でつりあってるとすれば、 実際には、$N_{1}$と$N_{2}$は、向きが逆で大きさが等しい力ということになるから、 一方の符号が正で、もう一方は負ということになる。
初期状態で長さ$\ell$だったばね要素に、$N_{1}$と$N_{2}$が
作用して、ばね要素が少し伸びて移動した状態でつりあっているとする。
1次元の世界なので$z$軸しかないが、重ねて描くと見づらくなるので、
「変形後」のばねを下にずらして描く。
節点の変位についても節点力と同様に、$z$軸方向を正の向きとして、
節点1の節点変位を$w_{1}$,
節点2の節点変位を$w_{2}$とする。
さて、このとき、
$N_{1}$, $N_{2}$, $k$, $w_{1}$, $w_{2}$の間にはどのような関係があるだろうか。
少し（10分ぐらい）考えてみよう。
実は、これらの関係を式で表したものが、ばねの剛性方程式になる。
使う知識としては、力のつりあい、フックの法則ぐらいでいい。
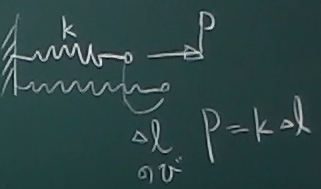フックの法則は、一端を壁に固定したばねの他端を力$P$で引っ張ったときに、
ばねが$\Delta\ell$だけ伸びたとすると、
$P$と$\Delta\ell$が比例する($P=k\Delta\ell$)という関係だ。
でも、節点変位の$w_{1}$や$w_{2}$はばねの伸びではない。
これは変位だ。
変位と伸びとは違う。
実は、中学や高校では、フックの法則を$F=kx$みたいな式で習うことが多く、
伸びに$x$を使うことが多い。
壁に一端が固定されたばねの場合、他端の変位はたまたまばね全体の伸びと一致
するが、今回の空中に浮くばねみたいに、
両端がともに変位する場合は、変位と伸びは一致しない。
それから、もう一つ。ばねの右端を引っ張る力$P$は、
この絵では外力だが、
例えば ばねの左端を壁から切り離してやれば、そこには反力が
作用しているはずだ。
そうすると、フックの法則の
$P=k\Delta\ell$（中学、高校の教科書ではしばしば$F=kx$）というのは、
この絵の状態のばねのときに、たまたま成り立つ式なのではないだろうか。
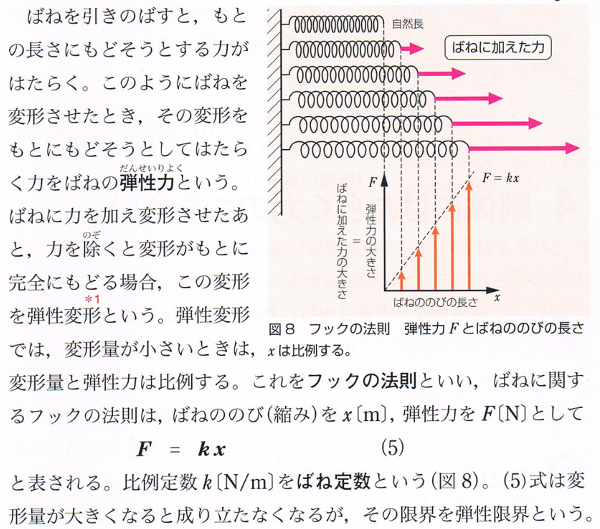そう思って、高校の教科書
（ちょっと古いが、2006年発行の東京書籍の「物理I」p.157）を見てみると、
割と正確に説明されている。
「変形をもとにもどそうとしてはたらく力」を「ばねの弾性力」と定義した上で、
「ばねに関するフックの法則は，ばねののび（縮み）を$x$[m]，
弾性力を$F$[N]として $F=kx$と表される」
とちゃんと書いてある。
弾性限界のこともちゃんと書いてある。
弾性力というのは、構造力学の言葉で言えば、
内力であり、軸力などの断面力のことだ。
つまり、フックの法則とういのは、
外力と変位の関係ではなくて、
内力と変形（のび）の関係を表した式なのだけど、
それを$F=kx$という式だけで覚えてしまうと、
そのうち、なんか$F$が外力のような気がしてきて、
$x$が変位のような気がしてきて、色々と誤解を生じたりするのではないかと思う。
もう一度、フックの法則を構造力学でなじんでいる表現でとらえなおすために、
ばねの軸力が見えるようにするには、
ばねをどこかで切ってやらないといけないが、
どこで切っても、
（引っ張り正の）軸力$N$が（向かい合う2つの）切断面に、
作用・反作用の関係で反対向きに作用している
（切断面をくっつけると、プラマイゼロで内力である軸力は見えなくなる）。
この軸力$N$とばね全体の伸び$\Delta\ell$との間に
$N=k\Delta\ell$の関係があるとういうのが、フックの法則の意味なのである。
左端が壁にくっついたばねの右端を$P$で引っ張った場合の軸力$N$は、
力のつりあいから（たまたま）$N=P$となる。
では、さきほどの空中($z$軸上)に浮かぶ ばね要素の伸び$\Delta\ell$を
$w_{1}$, $w_{2}$を使って表してみよう。
図の、初期状態（上）のばね要素の節点1から、
変形後（下）のばね要素の節点2までの長さを
2通りの方法で表せば、等式が作れる。
上のばね要素に着目すれば、$\ell+w_{2}$,
下のばね要素に着目すれば、$w_{1}+(\ell+\Delta\ell)$.
つまり、
$\ell+w_{2}=w_{1}+(\ell+\Delta\ell)$
から、
$\Delta\ell=w_{2}-w_{1}$
と求まる。
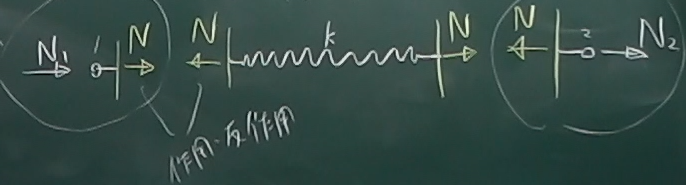ばねの伸びはわかったので、
次に「弾性力」つまり、ばねの軸力を求める。
ばね要素の軸力を
見えるようにするために、ばねの節点の近くを切り離してやろう。
この ばね要素が空中でつりあっているのであれば、
どこを切っても
（引っ張り正の）軸力$N$が（向かい合う2つの）切断面に、
作用・反作用の関係で反対向きに作用している
（切断面をくっつけると、プラマイゼロで内力である軸力は見えなくなる）。
ばね要素は、2箇所の切断面で3つのピースに分かれているが、
まずは、左端のピースについて力のつりあいを考えるなら、
$\Sigma\!\!\rightarrow=N_{1}+N=0$
となり、
$N_{1}=-N$
となる。右端のピースについて力のつりあいを考えるなら、
$\Sigma\!\!\rightarrow=-N+N_{2}=0$
となり、
$N_{2}=N$
となる。真ん中のピースは、正に理想的なフックの法則を表す図になっていて、
軸力$N$が一様に作用して、伸びが$\Delta\ell$なのだから、
$N=k\Delta\ell$
である。これに
$\Delta\ell=w_{2}-w_{1}$を代入すると、
$N=k(w_{2}-w_{1})$
となる。
さて、さっきの
$N_{1}=-N$と
$N_{2}=N$に
$N=k(w_{2}-w_{1})$
を代入すると、
$N_{1}=\;\;\; kw_{1}-kw_{2}$
$N_{2}=-kw_{1}+kw_{2}$
となり、
$N_{1}$, $N_{2}$, $k$, $w_{1}$, $w_{2}$の間に2つの関係式が
導かれる。
これをマトリクスの形に整理してやると、
$
\left(
\begin{array}{c}
N_{1}\\
N_{2}
\end{array}
\right)
=
\left(
\begin{array}{cc}
k & -k \\
-k & k
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}
\end{array}
\right)
$
となる。
これを1要素のばねの剛性方程式と言う。
後で、複数の要素を扱う場合、複数の要素の剛性方程式を重ね合わせたものを
「全体剛性方程式」と言うが、それに対して、
個々の要素の剛性方程式は要素剛性方程式と言う。
その意味では、1要素しかないが、これも要素剛性方程式である。
ここで、
節点力をまとめたベクトル
（横向きに書けば）$(N_{1}, N_{2})$を節点力ベクトルと言い、
節点変位をまとめたベクトル
（横向きに書けば）$(w_{1}, w_{2})$を節点変位ベクトルと言う。
$
\left(
\begin{array}{cc}
k & -k \\
-k & k
\end{array}
\right)
$
の部分を剛性行列とか剛性マトリクスと言う。
例題を解いてみる。
この授業でのマトリクス構造解析の問題は、
ばね構造系に既知の外力が与えられているとき、
節点変位を求め、その求めた節点変位を用いて反力（や断面力）を求め、
（それぞれの要素に切り離したときの）実際の力の向きを作図せよというような
問題となる。
図のように、1要素のばね要素が、節点1で壁にくっついていて、
節点2を外力$P$で右向きに引っ張られているものとする。
問題：このとき、(1)剛性方程式を用いて節点変位を求め、
(2)求めた節点変位を用いて反力を求め、
(3)ばね要素の各節点に作用する力を、正の値で描ける向きに矢印を向けて図示せよ。
これは、外力が既知変数で、節点変位を未知変数として求める場合の手順である。
外力が与えられている節点の節点力に外力を与える。
たとえば、この場合、節点2に右向きに外力$P$が作用しているから、
$N_{2}=P$である。
外力のない節点の節点力は、すべて0とする。
反力は、壁から切り離さないと見えないので、
外力としては0である。
切り離さないと見えない断面力などは、すべて0である。
切り離さなくても見えている外力だけを与える。
すると、剛性方程式は以下のようになる。
$
\left(
\begin{array}{c}
0\\
P
\end{array}
\right)
=
\left(
\begin{array}{cc}
k & -k \\
-k & k
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}
\end{array}
\right)
$
構造力学の問題は、 普通は、 空中に浮いている物体に作用する外力だけがつりあっている という問題ではなくて、 地面や壁にくっついた物体に外力が作用して、 地面や壁にくっついた部分に生じる反力と外力がつりあっている。 なので、地面や壁にくっついた部分で、 変位が0となり既知となるものが出てくる。 それが変位の境界条件となる。 この問題の場合、節点1は壁にくっついていて動かないので、 $w_{1}=0$である。 でも、この$w_{1}=0$を 剛性方程式に代入しないでほしい。 剛性方程式というのは、コンピューターで解くためのツールで、 今、節点変位ベクトルが未知変数として求まるように解こうとしているわけだから、 これを解いたときに、 答えとして$w_{1}=0$が求まるようにしたい。 そこで、剛性マトリクスに細工をする。 $2\times 2$のマトリクスだとあまりに特殊な場合で、 一般的な理解がしにくいので、まず、 節点力が4つあって、節点変位も4つある$4\times 4$のマトリクスの 場合について説明する。
$
\left(
\begin{array}{c}
N_{1}\\
N_{2}\\
N_{3}\\
N_{4}
\end{array}
\right)
=
\left(
\begin{array}{cc}
k_{11} & k_{12} & k_{13} & k_{14}\\
k_{21} & k_{22} & k_{23} & k_{24}\\
k_{31} & k_{32} & k_{33} & k_{34}\\
k_{41} & k_{42} & k_{43} & k_{44}
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}\\
w_{3}\\
w_{4}
\end{array}
\right)
$
このような剛性方程式で、例えば
$w_{3}=0$という境界条件を入れたいとする。
この代数方程式の節点変位ベクトルを未知変数として解いたときに、
$w_{3}=0$
が答えになるようにしたいということだ。
まず、3行目の
$N_{3}=
k_{31}w_{1} + k_{32}w_{2} + k_{33}w_{3} + k_{34}w_{4}$
から
$w_{3}=0$が求まってほしいので、
$
\left(
\begin{array}{c}
N_{1}\\
N_{2}\\
0 \\
N_{4}
\end{array}
\right)
=
\left(
\begin{array}{cc}
k_{11} & k_{12} & k_{13} & k_{14}\\
k_{21} & k_{22} & k_{23} & k_{24}\\
0 & 0 & 1 & 0 \\
k_{41} & k_{42} & k_{43} & k_{44}
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}\\
w_{3}\\
w_{4}
\end{array}
\right)
$
とする。更に、$w_{3}$が、$w_{1}, w_{2}, w_{4}$と連立されると困るので、
$
\left(
\begin{array}{c}
N_{1}\\
N_{2}\\
0 \\
N_{4}
\end{array}
\right)
=
\left(
\begin{array}{cc}
k_{11} & k_{12} & 0 & k_{14}\\
k_{21} & k_{22} & 0 & k_{24}\\
0 & 0 & 1 & 0 \\
k_{41} & k_{42} & 0 & k_{44}
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}\\
w_{3}\\
w_{4}
\end{array}
\right)
$
とする。
つまり、節点$n$で$w_{n}=0$の
境界条件を与える場合は、
節点力$N_{n}=0$,
剛性マトリクスの$k_{nn}=1$,
それ以外の$n$行および$n$列の成分はすべて0にする。
これをさきほどの1要素の ばねの問題
$
\left(
\begin{array}{c}
0\\
P
\end{array}
\right)
=
\left(
\begin{array}{cc}
k & -k \\
-k & k
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}
\end{array}
\right)
$
に適用すると、$w_{1}=0$だから、
$k_{11}=1$にして、その縦横は0なので、
$
\left(
\begin{array}{c}
0\\
P
\end{array}
\right)
=
\left(
\begin{array}{cc}
1 & 0 \\
0 & k
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}
\end{array}
\right)
$
となる。
これを解くと、
$0=w_{1}$
$P=kw_{2}$
となり、$w_{1}=0, w_{2}=\frac{P}{k}$と節点変位が求まる。
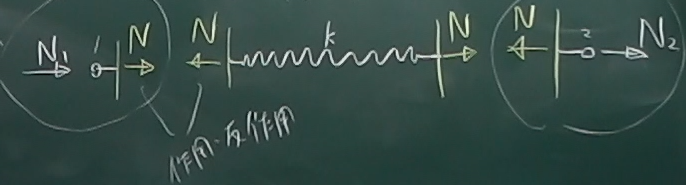求まった節点変位をもとの要素剛性方程式に代入すれば、
各節点を切断した場合の断面力が求まる。
さっき、ばね要素を節点の近くで切断し、3つのピースに切り離したときの、
真ん中のピースについて要素剛性方程式を適用しているイメージだ。
断面力を求める際に使う剛性方程式は、
（真ん中のピースはどこも固定されいないので）
境界条件を入れた剛性方程式ではなく、
もとの要素剛性方程式に節点変位を代入する。
つまり、もとの要素剛性方程式
$
\left(
\begin{array}{c}
N_{1}\\
N_{2}
\end{array}
\right)
=
\left(
\begin{array}{cc}
k & -k \\
-k & k
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}\\
w_{2}
\end{array}
\right)
$
に、
$w_{1}=0, w_{2}=\frac{P}{k}$を代入すると、
$
\left(
\begin{array}{c}
N_{1}\\
N_{2}
\end{array}
\right)
=
\left(
\begin{array}{cc}
k & -k \\
-k & k
\end{array}
\right)
\left(
\begin{array}{c}
0\\
\frac{P}{k}
\end{array}
\right)
$
つまり、
$N_{1}=-P$
$N_{2}=\;\;P$
と求まる。
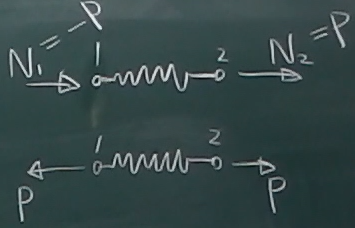これを図示すると、
まず、右向き正の$N_{1}$と$N_{2}$がそれぞれ$-P$と$P$なので、
$N_{1}$は実際には左向きに$P$の力で、
$N_{2}$は実際には右向きに$P$の力である。
つまり、ばね要素は両端を$P$で引っ張られてつりあっていることになる。
今、求めた節点力は、厳密には、
節点の近くで ばね要素を切断した切断面に生じる
（切ったことで見えるようになった）断面力に対応するが、
この場合、左側の節点力は反力に対応するし、
右側の節点力は（作用・反作用と力のつりあいから）外力と同じ値になるので、
単純に、反力と外力が求まったと解釈しておいてよい。
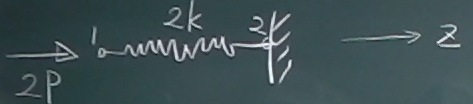図のように、ばね定数$2k$の
ばねが、右端が壁にくっついていて、左端が右側に$2P$で押されている。
このばねの左端を節点1, 右端を節点2とし、
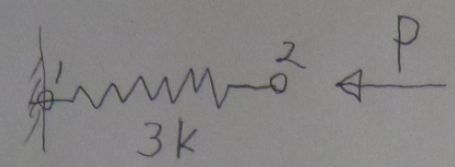1要素のばねの剛性方程式を用いて、
(1)節点変位を求め、
(2)
節点1, 2の近傍でばねを切断したときの断面力を、
求めた節点変位を用いて節点力$(N_{1}, N_{2})$として求め、
(3)（切断した）ばね要素の各節点に作用する力を、正の値で描ける向きに矢印を向けて図示せよ。
1要素のばねの剛性方程式を用いて、
(1)節点変位を求め、
(2)
節点1, 2の近傍でばねを切断したときの断面力を、
求めた節点変位を用いて節点力$(N_{1}, N_{2})$として求め、
(3)（切断した）ばね要素の各節点に作用する力を、正の値で描ける向きに矢印を向けて図示せよ。
解答
2022年度 小テスト
問1-3,
解答
2021年度 小テスト
問1-3,
解答
