
構造力学(基礎)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 棒のような細長い部材(ぶざい、構造物を構成する材料)から
組立てられている構造物を骨組というが、
3本の部材でできる三角形を基本要素として組立てられている
骨組をトラスと言う。
トラス構造は、例えばトラス橋に使われているので、
画像検索で実物のイメージをつかんでほしい。
三角にするのは、つぶれにくくなるからだ。
棒のような細長い部材(ぶざい、構造物を構成する材料)から
組立てられている構造物を骨組というが、
3本の部材でできる三角形を基本要素として組立てられている
骨組をトラスと言う。
トラス構造は、例えばトラス橋に使われているので、
画像検索で実物のイメージをつかんでほしい。
三角にするのは、つぶれにくくなるからだ。
例えば、窓枠みたいな四角い骨組は、力を加えると頂点部分
(普通はそこが部材どうしの接合部となっている)が変形して部材の回転を許してしまい、
平行四辺形状に変形しやすい。
 でも、三角形に組まれた骨組は、頂点部分が弱くて部材の回転を許したとしても、
例えば、写真のように頂点部分が回転できるようになっていたとしても、
四角形と違い、
部材が回転することでは、三角形はつぶれない。
でも、三角形に組まれた骨組は、頂点部分が弱くて部材の回転を許したとしても、
例えば、写真のように頂点部分が回転できるようになっていたとしても、
四角形と違い、
部材が回転することでは、三角形はつぶれない。
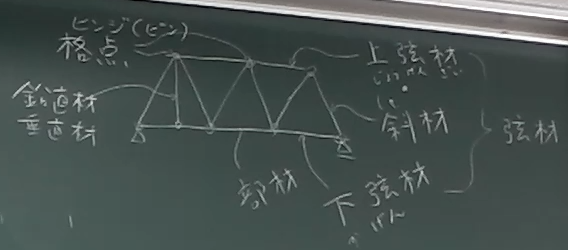
部材と部材がつないである接合部(写真ではボルトでつないでいるところ)を 節点と言う。 トラスの形に部材を組立てたときは、 節点は三角形の頂点になっているが、 特にトラスの節点(直線で理想化した三角形の頂点)のことを指すときは、格点という。
 橋桁にトラス構造が使われている橋をトラス橋というが、
トラス橋に関わる用語をいくつか覚えておこう。
トラスを構成する部材は、トラス部材と言えばよいが、
トラスのどこに使われているかを区別した呼び方がある。
トラスの上下に横向きに使われている部材は、弦材と呼び、
そのうち上側のものを
橋桁にトラス構造が使われている橋をトラス橋というが、
トラス橋に関わる用語をいくつか覚えておこう。
トラスを構成する部材は、トラス部材と言えばよいが、
トラスのどこに使われているかを区別した呼び方がある。
トラスの上下に横向きに使われている部材は、弦材と呼び、
そのうち上側のものを
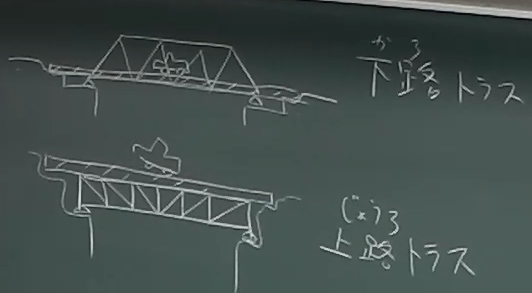 トラス橋では、
車の通る道路の位置の違いにより、区別する呼び方もある。
車の通る
道路がトラスの下側にあるものを
トラス橋では、
車の通る道路の位置の違いにより、区別する呼び方もある。
車の通る
道路がトラスの下側にあるものを
 また、トラスの三角形の形や並び方の違いで、様々な種類のトラスがある。
代表的な3つぐらいは覚えておこう。
図の一番上のトラスのように、
三角形を互い違いに並べた最も典型的なトラスは、
ワーレントラスとかワレントラスと呼ばれる。
四角形の対角線に斜材を入れたトラスもよくあるが、
斜材の向きによって名前が変わる。
斜材の向きは、左右対称になっているが、
真ん中を見て「ハ」の字に斜材が並んでいるものはハウトラス、
真ん中を見て「V」の字に斜材が並んでいるものはプラットトラスである。
ハがハウトラスでブイがプラットトラスだから、まあ、覚えやすい。
ちなみに、ワレンだのハウだのプラットというのは、
そのトラスを考案した人の名前である。
また、トラスの三角形の形や並び方の違いで、様々な種類のトラスがある。
代表的な3つぐらいは覚えておこう。
図の一番上のトラスのように、
三角形を互い違いに並べた最も典型的なトラスは、
ワーレントラスとかワレントラスと呼ばれる。
四角形の対角線に斜材を入れたトラスもよくあるが、
斜材の向きによって名前が変わる。
斜材の向きは、左右対称になっているが、
真ん中を見て「ハ」の字に斜材が並んでいるものはハウトラス、
真ん中を見て「V」の字に斜材が並んでいるものはプラットトラスである。
ハがハウトラスでブイがプラットトラスだから、まあ、覚えやすい。
ちなみに、ワレンだのハウだのプラットというのは、
そのトラスを考案した人の名前である。
 国内で見かけるトラス橋の部材の接合部は、
上弦材や下弦材から突き出した
ガセットプレートと言われるプレート部分に、
トラス部材がボルトでしっかりと連結されているものがほとんどだ。
部材どうしの交点に位置する格点がある場所には、
特に格点というべき部品みたいなものは存在していない。
国内で見かけるトラス橋の部材の接合部は、
上弦材や下弦材から突き出した
ガセットプレートと言われるプレート部分に、
トラス部材がボルトでしっかりと連結されているものがほとんどだ。
部材どうしの交点に位置する格点がある場所には、
特に格点というべき部品みたいなものは存在していない。
 一方で、
1900年代初頭にかけられた歴史的トラス橋とかだと、
格点部分が本当に回転するようになっていたりする。
写真は、カナダのケベック橋の例である。
これからみなさんに部材の力とかを解いてもらうトラスは、
格点部分が回転するようになっているトラスである。
一方で、
1900年代初頭にかけられた歴史的トラス橋とかだと、
格点部分が本当に回転するようになっていたりする。
写真は、カナダのケベック橋の例である。
これからみなさんに部材の力とかを解いてもらうトラスは、
格点部分が回転するようになっているトラスである。
ちなみに、このケベック橋の写真は、2014年に私が実物を撮影したものだが、
橋の全景
を
撮影できる場所を見つけるのになかなか苦労した。
 部材の太さ(や断面の形)を無視して線で表し、
格点が回転するように理想化したトラスのモデルを
トラスモデルと言う。
トラスモデルの格点部をヒンジ(「ちょうつがい」という意味)とかピンと
呼び、トラス部材は直線で、ヒンジは○で表す。
ただし、トラスモデルを描くときに、すべての格点に○を
描くのはめんどくさいので、トラスと言ったときは、
ヒンジの○を描かなくても、格点部分はヒンジと見なす。
部材の太さ(や断面の形)を無視して線で表し、
格点が回転するように理想化したトラスのモデルを
トラスモデルと言う。
トラスモデルの格点部をヒンジ(「ちょうつがい」という意味)とかピンと
呼び、トラス部材は直線で、ヒンジは○で表す。
ただし、トラスモデルを描くときに、すべての格点に○を
描くのはめんどくさいので、トラスと言ったときは、
ヒンジの○を描かなくても、格点部分はヒンジと見なす。
ヒンジで連結されたトラス部材は、つながっている部材が
回転しても、ヒンジ部分が回転してしまうので、
モーメントのような回転の力を伝達することができない。
また、両端がヒンジになっているため、
トラスの軸直角方向の力を伝達しようとしても、
写真のように2箇所のヒンジが回転してしまうので、
軸直角方向の力も伝達できない。
そうすると、トラス部材が伝達できる力は、
トラスの軸方向の力(軸力と言う)だけである。
つまり、トラスには軸力しか働かない。
だから、部材に作用する力を計算するのが楽である。
あれ、ちょっと、待ってほしい。
さっき、国内で見かけるほとんどのトラス橋の格点部は、
ガセットプレートになっていて、そこに部材がボルトでしっかりと
連結されていると言ったと思うが、
こんなふうに格点部がヒンジになっていないトラス橋は、
部材にモーメントだの様々な力が作用して、
計算が大変になるのではないだろうか。
もちろん、真面目に計算しようとしたら、大変だ。
それも、コンピューターの使えない時代に手計算だけでやろうとしたら、
さぞ大変だったろう。
今は、コンピューターを使えば、モーメントなどの影響も含めて、
トラス部材の力を計算することができるが、
トラスのような細長い部材では、
格点部がしっかりと固定されている(剛結という)として計算しても、
実は、モーメントなどの軸力以外の影響は小さいので、
格点部をヒンジと見なしたトラスモデルとして計算しても、
それほど違いはない。
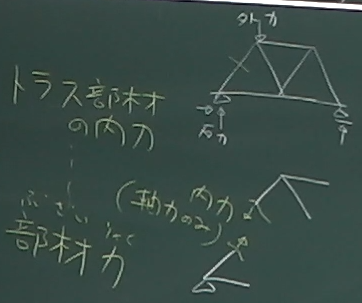 トラス構造が外力を受けた場合に、トラス部材にどのような内力が
生じるかは、計算できる。
しかも、トラス部材の内力は軸力しか発生しないので、
話が簡単である。
トラス部材を切断した切断面に生じる内力としての軸力のことを
部材力と呼び、
トラス構造が外力を受けた場合に、トラス部材にどのような内力が
生じるかは、計算できる。
しかも、トラス部材の内力は軸力しか発生しないので、
話が簡単である。
トラス部材を切断した切断面に生じる内力としての軸力のことを
部材力と呼び、
脱線:
私は
大学生のとき、
数学の授業で出てくる$\xi$のことを、
「ブザイ」と言うのだと思っていた。
実際には先生は「グザイ」と言っていたのだが。
それで、材料力学の授業でトラスの「ブザイリョク」というのが出てきたときは、
(この先生はなぜか部材力と板書しなかった)
てっきり$\xi$力と書くものだと思いこんでいた。
当時、同級生の友達と一緒に問題を解いたりもしたのだが、
その友達も$\xi$力でいんだよなと言っていたので、
最初は話が合っていた。
でもだんだん、おかしいような気がしてきた。
その友達は、数学の授業の$\xi$の方は「グザイ」と聞き取っていたのだけど、
トラスの部材力の方も「グザイリョク」と聞こえていたらしい。
それで、私とその友達とでは、勘違いの仕方は逆だったけど、
二人の間では、しばらく話が通じて勘違いに気づかなかったという話。
 第2回のところで静定・不静定
の話をちょっとだけしたけど、もう少しちゃんと説明する。
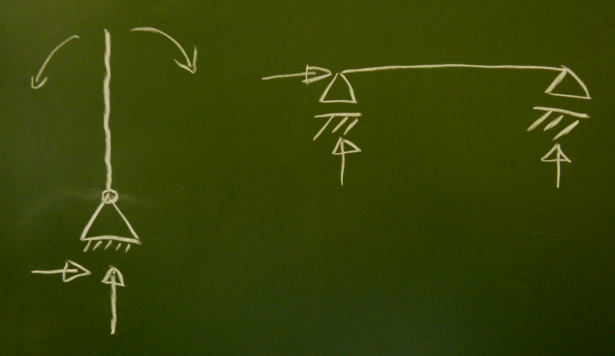
まず、反力が3個未満の場合。
例えば、反力2個のヒンジ支承に1本の棒を立てたら、
棒は回転して倒れてしまう。
あるいは、反力1個のローラー支承2個(反力の合計は2つ)で
棒を支えたら、棒は横に平行移動できてしまう。
このように、ちょっとでも外力を受けたら、
回転移動や平行移動をしてしまって自立しない構造を不安定であると言う。
ヒンジ支承1個(反力2つ)にローラー支承1個(反力1つ)で
支えられた構造など、反力の合計が3個以上になれば、一般には、
構造物は自立し、安定であると言える。
第2回のところで静定・不静定
の話をちょっとだけしたけど、もう少しちゃんと説明する。
まず、反力が3個未満の場合。
例えば、反力2個のヒンジ支承に1本の棒を立てたら、
棒は回転して倒れてしまう。
あるいは、反力1個のローラー支承2個(反力の合計は2つ)で
棒を支えたら、棒は横に平行移動できてしまう。
このように、ちょっとでも外力を受けたら、
回転移動や平行移動をしてしまって自立しない構造を不安定であると言う。
ヒンジ支承1個(反力2つ)にローラー支承1個(反力1つ)で
支えられた構造など、反力の合計が3個以上になれば、一般には、
構造物は自立し、安定であると言える。
 ただし、反力が3個以上でも、不安定な場合もある。
図のように、ローラー支承を1直線上に並べて、
平行移動ができるような構造や、
1点の回りに回転ができるようにローラー支承を円周上に配置した構造は、
反力が3個以上でも不安定である。
ただし、反力が3個以上でも、不安定な場合もある。
図のように、ローラー支承を1直線上に並べて、
平行移動ができるような構造や、
1点の回りに回転ができるようにローラー支承を円周上に配置した構造は、
反力が3個以上でも不安定である。
反力が3個で安定な構造は、
第2回の反力の計算でやったように、
2次元では鉛直方向のつりあい、水平方向のつりあい、ある点回りのモーメントのつりあいの3つの式が使えるから、
3つの反力を未知数とすれば、
3つのつりあいの式を連立させて、反力を求めることができる。
このように、力のつりあいから反力を求めることができる構造を
外的静定であると言う。
反力が4つ以上あって、力のつりあいからは反力を求められない構造を
外的不静定であると言う。
更に、部材力などの内力も力のつりあいだけから求まる構造を内的静定であると言い、
力のつりあいだけでは部材力などの内力が求まらない構造を内的不静定であると言う。
つまり、まとめると以下のようになる。
外的不静定の構造でも反力がわかっている場合は、
それに対して内的静定・内的不静定という区別はありえるが、
今のところ、内的静定・不静定の話は、反力の求まる外的静定の構造に
限定していおいていいだろう。
力のつりあいから構造物の反力を求める場合は、
外的静定でないと解けないし、
力のつりあいから
トラスの部材力などを求める場合には内的静定でないと解けないので、
外的静定かどうか、内的静定かどうかを判定することは重要である。
といっても、外的静定かどうかというのは、
反力を数えればいい(あとは、平行移動できるようになってたり、
回転できるようになってたりしないかを確認すればいい)だけなので、
特に難しい話ではないが、
内的静定かどうかを判定するには、
以下のような式を用いる。
$m+r-2j>0 \cdots$内的不静定
$m+r-2j=0 \cdots$内的静定
$m\cdots$ 部材の数(memberのm)
$r\cdots$ 反力の数(reaction forceのr)
$j\cdots$ 格点の数(jointのj)
どうしてこの式で判定できるのかを大雑把に説明しておく。
格点が上下・左右に動かないようにするには、
上下・左右(または、斜めでもいいが)の2方向の変位を拘束する
必要がある。つまり、拘束されていない格点は、2方向に動けるので、
2つの自由度があることになる。
もし、(ばらばらの)格点が$j$個あれば、自由度は$2j$ということになる。
さて、2つの格点(ばらばらであれば、自由度は4)を
1本の部材でつないだとする。
そうすると、2つの格点の距離は、一定に保たれるので、
自由度が1つ減り、自由度は3となる。
例えば、2つの格点の座標がそれぞれ、$(a,b)$, $(c,d)$みたいに
表されていたとすると、2つの格点がばらばらなら、$a,b,c,d$は、
自由な値を取れるから自由度は4だが、2つの格点の距離が$\ell$と決められて
しまうと、ある1つの座標(例えば$a$)は、残りの$b,c,d$と$\ell$を
使って表せてしまうことになるから、自由度は3ということ。
つまり、格点がいっぱいあって、その中の
2つの格点をつないでいる部材が$m$本あると、
拘束が$m$個 増え、自由度が$m$個 減るということ。
というわけで、部材による拘束の数$m$と、
反力による拘束の数$r$の合計が、格点の自由度$2j$と等しくなると、
すべての格点が拘束されるということ。
 では、反力3個で外的静定なトラスについて、内的静定・内的不静定を判定してみよう。
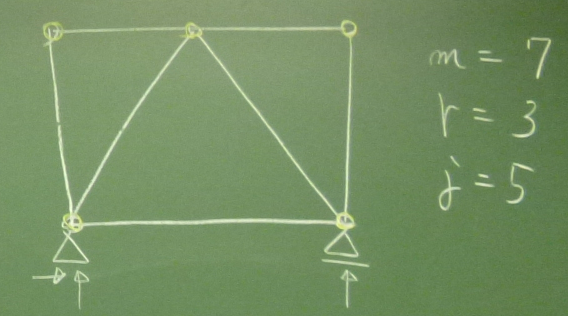
まず、右の図のようなトラスの場合、
部材は7本だから$m=7$, 反力は3つだから$r=3$, 格点は5個だから$m=5$.
これらを上の式に代入すると、
では、反力3個で外的静定なトラスについて、内的静定・内的不静定を判定してみよう。
まず、右の図のようなトラスの場合、
部材は7本だから$m=7$, 反力は3つだから$r=3$, 格点は5個だから$m=5$.
これらを上の式に代入すると、
$m+r-2j=7+3-2\times 5=0$
となるから、このトラスは内的静定だ。
ちなみに、内的静定なトラスを単に「静定トラス」と言うことも多い。
静定トラスでないと、トラスは力のつりあいだけでは解けない。
格点がヒンジになっている
静定トラスは、どこか1本の部材でも破断すると、
内的不安定になり、自立しない構造になってしまうので、
構造全体が崩壊してしまう。
格点部が剛結されているトラス構造の場合は多少の冗長性を発揮するかも
しれないが、構造としてはそういう危険性を含んでいる。
一方、不静定トラスの場合、
部材が1本 破断したとしても、構造として自立しなくなるわけではないので、
残りの部材に力が再分配される。
こういう構造的な余裕のことを冗長性と言ったりする。
静定トラスは、力のつりあいだけで解けて、計算が簡単だから、
みなさんには、まず静定トラスの計算をやってもらうけど、
(あるいはコンピューターで構造解析ができない時代には、
静定トラスがたくさん作られたかもしれないが)、
静定構造で計算が簡単だということは、別に、
構造物として優れているということではなない。
もちろん、構造物の用途によっては、静定構造にした方が有利だと
いうこともあるだろう。
構造力学では、トラスでも梁でも最初に計算の簡単な静定構造ばかりやるけど、
それが構造物の標準というわけではないことは覚えておいてほしい。
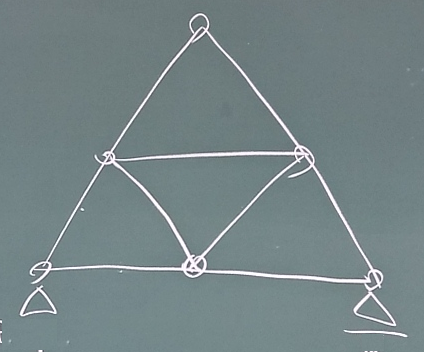
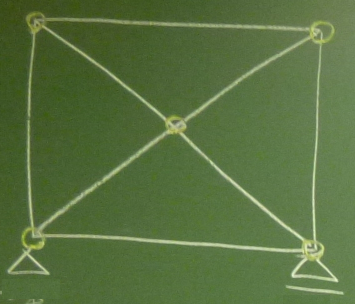 以下のトラスについて内的静定か内的不静定かを判定してみよう。
以下のトラスについて内的静定か内的不静定かを判定してみよう。
答えはここ。
 答えはここ。
答えはここ。
 答えはここ。
答えはここ。
2024年度小テスト第2回:
小テスト240510
2020年度 小テスト:
問1,
解答