
構造力学(基礎)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 私は中学の理科でも高校の物理でも、物体に作用する力というのが
よく分からなかった。
例えば、中学のときにこんな問題を出された。
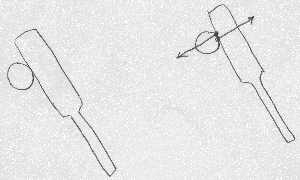
図のようなラケットがピンポン玉を打ち付けている絵の中に
「作用する力を書き入れよ」みたいな問題ではなかったかと思う。
で、正解はどんなものだったかよく覚えていないのだが、
確か、ラケットがピンポン玉を押す力とその反作用力として
ピンポン玉がラケットを押し返す力は書き入れるべき「作用する力」だったと
思う。その他にもラケットをにぎる手との関係もあったかも知れない。
そして、力の作用点もラケットとピンポン玉の重心あたりに
書かれていたかも知れない。
で、私はその正解を見ても、まるで理解できずに混乱しまくっていた。
というのは、ラケットに接着剤がついていて、ピンポン玉を打った瞬間に
ラケットとピンポン玉がねっぱって一体化したらどうなるのだろうかと考えたら、
なにがなんだか分からなくなってしまった。
私は中学の理科でも高校の物理でも、物体に作用する力というのが
よく分からなかった。
例えば、中学のときにこんな問題を出された。
図のようなラケットがピンポン玉を打ち付けている絵の中に
「作用する力を書き入れよ」みたいな問題ではなかったかと思う。
で、正解はどんなものだったかよく覚えていないのだが、
確か、ラケットがピンポン玉を押す力とその反作用力として
ピンポン玉がラケットを押し返す力は書き入れるべき「作用する力」だったと
思う。その他にもラケットをにぎる手との関係もあったかも知れない。
そして、力の作用点もラケットとピンポン玉の重心あたりに
書かれていたかも知れない。
で、私はその正解を見ても、まるで理解できずに混乱しまくっていた。
というのは、ラケットに接着剤がついていて、ピンポン玉を打った瞬間に
ラケットとピンポン玉がねっぱって一体化したらどうなるのだろうかと考えたら、
なにがなんだか分からなくなってしまった。
 高校のときには、こんな問題を出された。
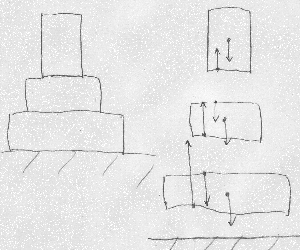
図のように墓石(だったかなあ?)が3段ぐらい重なっているとき、
それぞれの墓石に作用する力をすべて書き入れよというような問題だったと思う。
そのときの先生は墓石を切り離してばらばらにするとわかりやすくなる
と言っていて、ばらばらの墓石に、それ自身の自重や、上の墓石から押される力や、
それらにより下の墓石から押し返される反作用力などなどを書き入れたものが
正解だったような気がするが、この正解も(理解できなかったので)よく
覚えていない。
このときも同様に、接着剤で墓石どうしをねっぱしてしまったらどうなるのか? とか、
墓石の途中を切って分割したらどうなるのか? ということを考えてしまうと、
どうしてそんなふうに都合よく、たまたま墓石どうしのさかいめに作用している
上からの重さと下からの反作用力が、それぞれの墓石に作用していることになるのか、
さっぱり訳がわからなくて混乱していた。
高校のときには、こんな問題を出された。
図のように墓石(だったかなあ?)が3段ぐらい重なっているとき、
それぞれの墓石に作用する力をすべて書き入れよというような問題だったと思う。
そのときの先生は墓石を切り離してばらばらにするとわかりやすくなる
と言っていて、ばらばらの墓石に、それ自身の自重や、上の墓石から押される力や、
それらにより下の墓石から押し返される反作用力などなどを書き入れたものが
正解だったような気がするが、この正解も(理解できなかったので)よく
覚えていない。
このときも同様に、接着剤で墓石どうしをねっぱしてしまったらどうなるのか? とか、
墓石の途中を切って分割したらどうなるのか? ということを考えてしまうと、
どうしてそんなふうに都合よく、たまたま墓石どうしのさかいめに作用している
上からの重さと下からの反作用力が、それぞれの墓石に作用していることになるのか、
さっぱり訳がわからなくて混乱していた。
 ちなみに、最近の中学の教科書 例えば
『理科I分野上』〜実験から自然のしくみを見つける〜
(教育出版株式会社、平成18年1月10日発行)
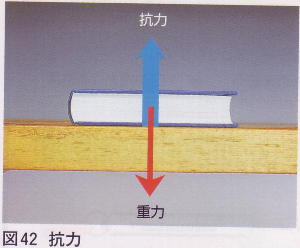
には、図のように机の上に本がのった写真で、重力と抗力がつりあうことが
説明されている。
重力と抗力を左右にずらして書き入れると(上の墓石の絵が正にそうだけど)、
モーメントがつりあわなくなってしまうので、
抗力の方を太くして、重力と一直線上に書き入れるという工夫をしているのだろう。
それはともかく、机の上にのっているのが本だったりすると、
やはり、私は、この本の135ページ目と136ページ目の間には、
同じように135ページぶんの重力と抗力とが作用していないのだろうかとか、
本と机を接着剤でくっつけたらどうなるのだろうかと考えてしまう。
ちなみに、最近の中学の教科書 例えば
『理科I分野上』〜実験から自然のしくみを見つける〜
(教育出版株式会社、平成18年1月10日発行)
には、図のように机の上に本がのった写真で、重力と抗力がつりあうことが
説明されている。
重力と抗力を左右にずらして書き入れると(上の墓石の絵が正にそうだけど)、
モーメントがつりあわなくなってしまうので、
抗力の方を太くして、重力と一直線上に書き入れるという工夫をしているのだろう。
それはともかく、机の上にのっているのが本だったりすると、
やはり、私は、この本の135ページ目と136ページ目の間には、
同じように135ページぶんの重力と抗力とが作用していないのだろうかとか、
本と机を接着剤でくっつけたらどうなるのだろうかと考えてしまう。
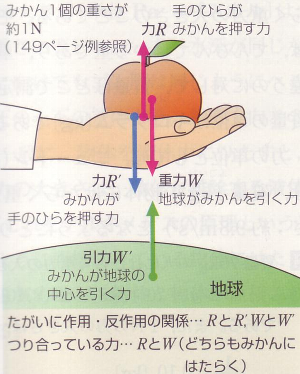 最近の高校の教科書の例として
『物理I』(東京書籍、平成18年2月10日発行)を見てみると、
重力(地球がみかんを引く力)と引力(みかんが地球の中心を引く力)が作用・反作用の
関係にあり、
みかんが手のひらを押す力と手のひらがみかんを押す力が作用・反作用の関係に
あり、
つりあっているのは、重力と手のひらがみかんを押す力という説明になっている。
手のひらがみかんを押す力は、
みかんが手のひらを押す力の反作用力であって、
重力の反作用力ではなない(重力の反作用力は引力だ)ということを
厳密に説明しようとしているのだろうと思う。
でも、この図でも「接着剤のパラドックス」は免れない。
手に接着剤がついていてみかんとねっぱってしまったらどうなるのだろうか?
みかんのまんなかあたりに水平に切れ目を入れたらどうなるのだろうか?
もちろん、どこがくっつこうが、どこが切り離れようが、
作用している力に変わりはない筈だ。
なんか、物体と物体の境目に着目してそこに作用する力だけを
ピックアップするのが暗黙の了解になっていないだろうか。
そのせいで中学、高校時代の私は混乱しまくっていた訳だが、
構造力学においては、自分で着目したい部分を意識的に切断して二つの部分に
切り離し、切り離されたそれぞれの系についてつりあいを考えるという
操作を行う。
大学でこのやり方を教わって、ようやく私は中学や高校時代の
物体と物体の境目に作用する力をどう扱えばいいのかが分かった。
物体と物体とを接着剤でくっつけたとしても、
その境目に作用する力は(他の任意の場所で切断した場合と同様に)
「内力」として考えてやればいいのだ。
最近の高校の教科書の例として
『物理I』(東京書籍、平成18年2月10日発行)を見てみると、
重力(地球がみかんを引く力)と引力(みかんが地球の中心を引く力)が作用・反作用の
関係にあり、
みかんが手のひらを押す力と手のひらがみかんを押す力が作用・反作用の関係に
あり、
つりあっているのは、重力と手のひらがみかんを押す力という説明になっている。
手のひらがみかんを押す力は、
みかんが手のひらを押す力の反作用力であって、
重力の反作用力ではなない(重力の反作用力は引力だ)ということを
厳密に説明しようとしているのだろうと思う。
でも、この図でも「接着剤のパラドックス」は免れない。
手に接着剤がついていてみかんとねっぱってしまったらどうなるのだろうか?
みかんのまんなかあたりに水平に切れ目を入れたらどうなるのだろうか?
もちろん、どこがくっつこうが、どこが切り離れようが、
作用している力に変わりはない筈だ。
なんか、物体と物体の境目に着目してそこに作用する力だけを
ピックアップするのが暗黙の了解になっていないだろうか。
そのせいで中学、高校時代の私は混乱しまくっていた訳だが、
構造力学においては、自分で着目したい部分を意識的に切断して二つの部分に
切り離し、切り離されたそれぞれの系についてつりあいを考えるという
操作を行う。
大学でこのやり方を教わって、ようやく私は中学や高校時代の
物体と物体の境目に作用する力をどう扱えばいいのかが分かった。
物体と物体とを接着剤でくっつけたとしても、
その境目に作用する力は(他の任意の場所で切断した場合と同様に)
「内力」として考えてやればいいのだ。
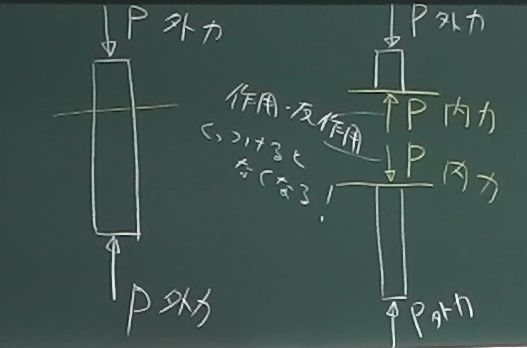 棒が図のように空中に浮いていて、上と下から
$P$の力で圧縮されていたとしよう。
このように、物体の外側からその表面に作用する力を「外力」と呼ぶことにする。
つまり、空中に浮いている棒が、上下からそれぞれ$P$の外力で押されて
つりあっている。
さて、
この棒の適当なところに切れ目を入れて切断して考えてみる。
切り離された上の部分は、上の部分だけでつりあっていると考えると、
上の部分の切断面には、上から押している外力$P$とつりあうような、
上向きに$P$の力が作用していないといけない。
この切断面に作用しているであろう力は、
棒を切らない状態では見えない力で、
棒の内部に圧力のように作用している内部の力なので「内力」と呼ぶことにする。
同様に、切り離された下の部分は下の部分だけでつりあっていると考えると、
下の部分の切断面には、下から押している外力$P$とつりあうような、
下向きに$P$の内力が作用していないといけない。
この切断面は、もともと棒に切れ目が入っていて、
上下から押されてくっついていたと考えれば、
作用反作用の関係が成り立つから、
いずれにせよ、上の切断面に作用する上向きの内力$P$と、
下の切断面に作用する下向きの内力$P$は、
切断面をくっつけるとプラマイゼロで(外力としては)なくなって
(見えなくなって)しまう。
棒が図のように空中に浮いていて、上と下から
$P$の力で圧縮されていたとしよう。
このように、物体の外側からその表面に作用する力を「外力」と呼ぶことにする。
つまり、空中に浮いている棒が、上下からそれぞれ$P$の外力で押されて
つりあっている。
さて、
この棒の適当なところに切れ目を入れて切断して考えてみる。
切り離された上の部分は、上の部分だけでつりあっていると考えると、
上の部分の切断面には、上から押している外力$P$とつりあうような、
上向きに$P$の力が作用していないといけない。
この切断面に作用しているであろう力は、
棒を切らない状態では見えない力で、
棒の内部に圧力のように作用している内部の力なので「内力」と呼ぶことにする。
同様に、切り離された下の部分は下の部分だけでつりあっていると考えると、
下の部分の切断面には、下から押している外力$P$とつりあうような、
下向きに$P$の内力が作用していないといけない。
この切断面は、もともと棒に切れ目が入っていて、
上下から押されてくっついていたと考えれば、
作用反作用の関係が成り立つから、
いずれにせよ、上の切断面に作用する上向きの内力$P$と、
下の切断面に作用する下向きの内力$P$は、
切断面をくっつけるとプラマイゼロで(外力としては)なくなって
(見えなくなって)しまう。
 では、地面にくっついている棒を上から押してみたらどうだろう。
ちょうど地面のところで切り離してやれば、
上の例と同様に、
切り離された上側の棒の切断面には、上向きの内力$P$が作用し、
切り離された下側の地面の切断面には、下向きに内力$P$が作用しているだろう。
このように棒を地面から切り離したときに、
切り離された棒側の切断面に作用している上向き内力のことを棒の「反力」と
呼ぶ
(後述するが、ここの2つめの解釈)。
平たく言えば、上から押された棒が地面から受ける反作用力ということだ。
では、地面にくっついている棒を上から押してみたらどうだろう。
ちょうど地面のところで切り離してやれば、
上の例と同様に、
切り離された上側の棒の切断面には、上向きの内力$P$が作用し、
切り離された下側の地面の切断面には、下向きに内力$P$が作用しているだろう。
このように棒を地面から切り離したときに、
切り離された棒側の切断面に作用している上向き内力のことを棒の「反力」と
呼ぶ
(後述するが、ここの2つめの解釈)。
平たく言えば、上から押された棒が地面から受ける反作用力ということだ。
さて、この図で、棒から切り離された地面は、 下向きに$P$の内力で押されていることになるが、 この力は、いったいどの力とつりあうのだろうか。 地面だけを考えたときに、 地面に下向きに$P$の力しか作用していなければ、 当然つりあわないわけで、 つりあうためには、上向きに$P$の力も作用していなければならない。 一体どこに作用しているのだろうか。 ちょっと考えてみてほしい。 黒板の右端に私の手が写っているが、これがヒント。 答え (すぐにはクリックしないで、ちょっと考えてみよう)。 要は、棒を下向きの外力$P$で押すとはいっても、 どこかに反力を取らなければ押せないということ。
前の回は、空中に浮いている物体の話だけど、
土木で対象とする一般的な構造物は、地面や崖(壁)とくっついている。
構造物を地面や壁とくっつけて固定することを「支持する」というけど、
支持するために構造物と地面や壁をくっつけている装置を
梁などが(剛体とみなせるほどに)堅い壁に埋め込んであるのを
モデル化したのは固定支承
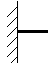 である(梁の場合には固定端とか埋め込み端とも呼ばれる)。
固定支承には、鉛直方向反力、水平方向反力、モーメント反力が生じる。
である(梁の場合には固定端とか埋め込み端とも呼ばれる)。
固定支承には、鉛直方向反力、水平方向反力、モーメント反力が生じる。
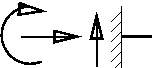 鉛直方向反力は(土木構造物では上向き反力を生じるのが一般的なので)
上向き正とするのが普通である。
水平方向反力は、右方向(梁の軸に沿って取った座標方向)を正とする場合と
梁の軸力の引張または圧縮に対応させて正負を決める場合とがあるだろう。
このテキストでは梁の水平方向反力が生じる問題はそれほど多くは扱わないが、
出てきたときに反力の正の向きを定義することにする。
モーメント反力の向きは、梁の下側が引張になる向きを正にするのが
一般的であろう。すると、両端固定の梁の場合、左端のモーメント反力は
右回りで、右端のモーメント反力は左回りということになるが、
この辺の話は内力の向きのところで改めて詳述する。
鉛直方向反力は(土木構造物では上向き反力を生じるのが一般的なので)
上向き正とするのが普通である。
水平方向反力は、右方向(梁の軸に沿って取った座標方向)を正とする場合と
梁の軸力の引張または圧縮に対応させて正負を決める場合とがあるだろう。
このテキストでは梁の水平方向反力が生じる問題はそれほど多くは扱わないが、
出てきたときに反力の正の向きを定義することにする。
モーメント反力の向きは、梁の下側が引張になる向きを正にするのが
一般的であろう。すると、両端固定の梁の場合、左端のモーメント反力は
右回りで、右端のモーメント反力は左回りということになるが、
この辺の話は内力の向きのところで改めて詳述する。
モーメント反力が生じないように構造物を支持している点が回転できるように
したのがヒンジ支承
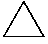 である。ピン支承とか回転支承とかとも言う。
三角形の積木のてっぺんのとんがったところに、
構造物がのっかるイメージである。
実物のイメージは
画像検索
してみてほしい。
(水平な地面に設置された)
ピン支承には鉛直方向反力と水平方向反力が生じる。
である。ピン支承とか回転支承とかとも言う。
三角形の積木のてっぺんのとんがったところに、
構造物がのっかるイメージである。
実物のイメージは
画像検索
してみてほしい。
(水平な地面に設置された)
ピン支承には鉛直方向反力と水平方向反力が生じる。
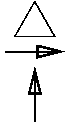 鉛直方向反力は(土木構造物では上向き反力を生じるのが一般的なので)
上向き正で与えられるのが普通である。
水平方向反力は、右方向(梁の軸に沿って取った座標方向)を正とするのが
一般的である。
鉛直方向反力は(土木構造物では上向き反力を生じるのが一般的なので)
上向き正で与えられるのが普通である。
水平方向反力は、右方向(梁の軸に沿って取った座標方向)を正とするのが
一般的である。
ピン支承の水平方向反力
(支承が傾いた地面や壁に設置される場合を考慮するなら、
設置面に平行な反力)が生じないように、
支承が設置面に平行に移動できるようにしたのがローラー支承
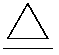 である。移動支承ともいう。三角形の積木の下にローラーが取り付けてあって、
積木が地面に対して水平に移動できるというイメージである。
実物のイメージは
画像検索
してみてほしい。
(水平な地面に設置された)
ローラー支承には鉛直方向反力のみが生じる。
である。移動支承ともいう。三角形の積木の下にローラーが取り付けてあって、
積木が地面に対して水平に移動できるというイメージである。
実物のイメージは
画像検索
してみてほしい。
(水平な地面に設置された)
ローラー支承には鉛直方向反力のみが生じる。
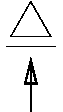 鉛直方向反力は(土木構造物では上向き反力を生じるのが一般的なので)
上向き正で与えられるのが普通である。
鉛直方向反力は(土木構造物では上向き反力を生じるのが一般的なので)
上向き正で与えられるのが普通である。
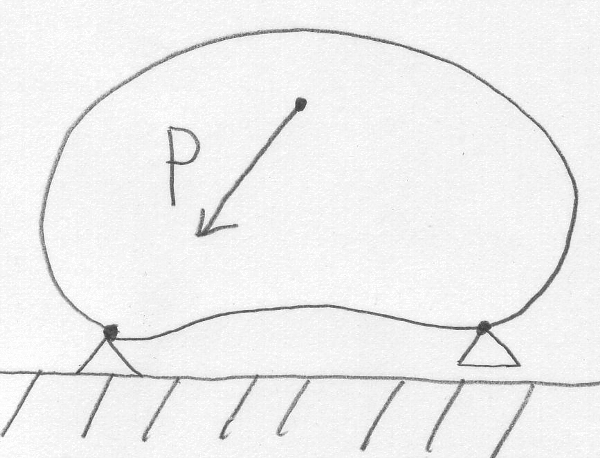 自重を無視できる物体が、図のようにヒンジ支承とローラー支承で
地面に支持されていて、外力$P$を受けているとする。
このとき、支点に生じる反力を求めたい。
自重を無視できる物体が、図のようにヒンジ支承とローラー支承で
地面に支持されていて、外力$P$を受けているとする。
このとき、支点に生じる反力を求めたい。
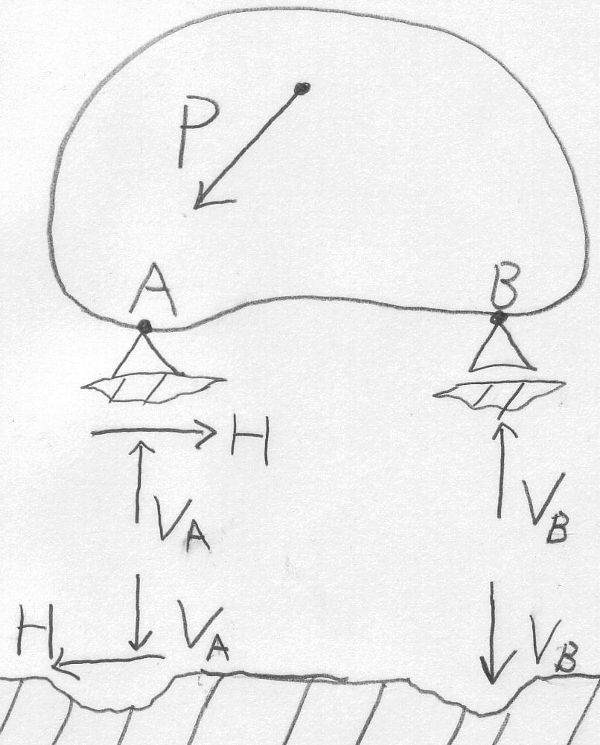 反力というのは、支点が支持している物体から受ける力の反作用力であるが、
支点が物体から受ける力と反力とを一つの絵の中に一緒に書くと
(中学や物理の教科書では正にそういう書き方がされていて
私は混乱したものだが)わかりにくいので、支点部分を地面から
切り取って考えることにすると、空中に浮いている物体の支点部分に、
外力が作用していて、物体は静止し続けている(つりあっている)と
考えることもできる。
物体や地面や壁を切り取った場合、切り取った面(切断面)には、
作用・反作用の法則により逆向きで大きさの等しい力がそれぞれ作用している。
このうち、空中に浮かぶことになった支点の側の切断面には、
支承の章で定義された支承の種類に応じた反力が
作用していると考えればよい。
つまり、支点反力というのは、
「空中に浮いている物体が静止し続けていられるように支点に作用する外力」と
考えることもできるし、
「支点直下の地面を切り取ったときに、その切断面に作用する内力」と
考えることもできる。
反力というのは、支点が支持している物体から受ける力の反作用力であるが、
支点が物体から受ける力と反力とを一つの絵の中に一緒に書くと
(中学や物理の教科書では正にそういう書き方がされていて
私は混乱したものだが)わかりにくいので、支点部分を地面から
切り取って考えることにすると、空中に浮いている物体の支点部分に、
外力が作用していて、物体は静止し続けている(つりあっている)と
考えることもできる。
物体や地面や壁を切り取った場合、切り取った面(切断面)には、
作用・反作用の法則により逆向きで大きさの等しい力がそれぞれ作用している。
このうち、空中に浮かぶことになった支点の側の切断面には、
支承の章で定義された支承の種類に応じた反力が
作用していると考えればよい。
つまり、支点反力というのは、
「空中に浮いている物体が静止し続けていられるように支点に作用する外力」と
考えることもできるし、
「支点直下の地面を切り取ったときに、その切断面に作用する内力」と
考えることもできる。
通常は、地面から切り離された物体を空中に浮かせて
(支承には反力を作用させて、つまり右の図の上の部分だけを見て)力のつりあいを考える。
左側の支点を$A$, 右側の支点を$B$とし、
支点$A$のヒンジ支承に生じる水平反力を右向き正として$H$,
支点$A$のヒンジ支承に生じる鉛直反力を上向き正として$V_{A}$,
支点$B$のヒンジ支承に生じる鉛直反力を上向き正として$V_{B}$とする。
ちなみに、$H$とか$V$という記号は、
英語のhorizontalやverticalから取っている。
テキストによっては$R$を使うものもあるが、これは、reaction forceとかから
取ったのだろう。まあ、記号は何でもいいのだが。
ここで、$V_{A}$などの反力は、向きが上向きとか既に決まっているので、
ベクトルではない。$V_{A}=10$N といった力の次元の数値が入る
スカラー量である。$V_{A}=-10$N みたいにマイナスの数値であれば、
実際には下向きに10Nの力という意味になる。
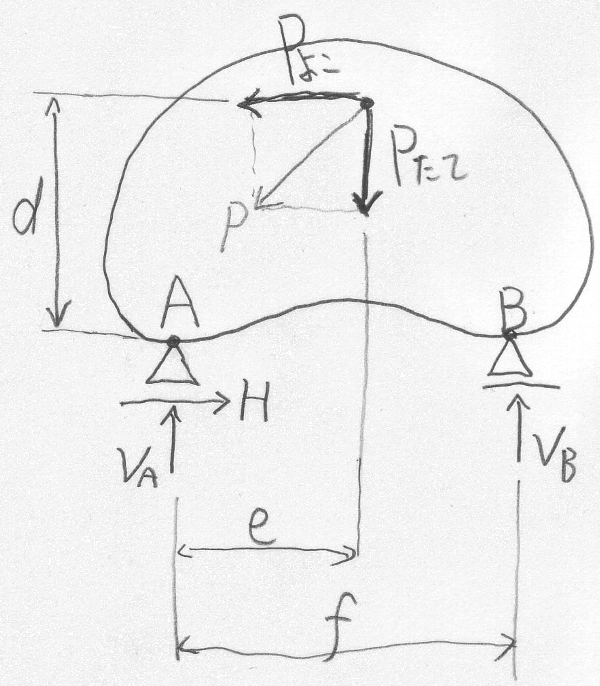 力の分解・整理の章の要領で、
外力$P$をたて方向成分$P_{たて}$とよこ方向成分$P_{よこ}$に分解する。
この物体は支点で地面につなぎとめられた「静止し続ける」物体だから、
力のつりあい条件から次の3式がなりたつ。
力の分解・整理の章の要領で、
外力$P$をたて方向成分$P_{たて}$とよこ方向成分$P_{よこ}$に分解する。
この物体は支点で地面につなぎとめられた「静止し続ける」物体だから、
力のつりあい条件から次の3式がなりたつ。
鉛直方向のつりあい(下向き正): $\Sigma\downarrow=(+P_{たて})+(-V_{A})+(-V_{B})=0$
水平方向のつりあい(右向き正): $\Sigma\rightarrow=(-P_{よこ})+(+H)=0$
A点回りのモーメントのつりあい(左回り正):
$\Sigma_{A}$ $=+P_{よこ}d-P_{たて}e+V_{B}f=0$
$=+P_{よこ}d-P_{たて}e+V_{B}f=0$
$\Sigma\downarrow$の記号は、下方向を+として鉛直方向の力をすべて足し算するという意味。
上向きの矢印↑で$V_{A}$の値を持つ力は、
下向きの矢印↓で描けば$-V_{A}$の値を持つことになる。
$\Sigma\rightarrow$は、右向きを正として横方向の力をすべて足し算する意味である。
$\Sigma_{A}$ は点$A$を中心に左回りを正として、
点$A$回りのモーメントをすべて足し算するという意味である。
右の図では、反力$H$と$V_{A}$は見やすいようにヒンジ支承の三角の下に
描き込まれているが、実際の作用点は点$A$なので、
これらの反力は点$A$回りにはモーメントを作らない。
$P_{よこ}$
が点$A$まわりにつくるモーメントの向きは、
点$A$を回転中心として、
$P_{よこ}$の方向(つまり左方向)に引っ張ったら、
物体は左回りするので、左回り正で足し算する場合は、プラスとなる。
$P_{たて}$
が点$A$まわりにつくるモーメントの向きは、
点$A$を回転中心として、
$P_{たて}$の方向(つまり下方向)に引っ張ったら、
物体は右回りするので、左回り正で足し算する場合は、マイナスとなる。
は点$A$を中心に左回りを正として、
点$A$回りのモーメントをすべて足し算するという意味である。
右の図では、反力$H$と$V_{A}$は見やすいようにヒンジ支承の三角の下に
描き込まれているが、実際の作用点は点$A$なので、
これらの反力は点$A$回りにはモーメントを作らない。
$P_{よこ}$
が点$A$まわりにつくるモーメントの向きは、
点$A$を回転中心として、
$P_{よこ}$の方向(つまり左方向)に引っ張ったら、
物体は左回りするので、左回り正で足し算する場合は、プラスとなる。
$P_{たて}$
が点$A$まわりにつくるモーメントの向きは、
点$A$を回転中心として、
$P_{たて}$の方向(つまり下方向)に引っ張ったら、
物体は右回りするので、左回り正で足し算する場合は、マイナスとなる。
このように二次元の力のつりあい条件は3本の式で表されるので、
未知数となる反力が3個であれば、力のつりあい条件のみから反力を求めることができる。
例えば、上の例では、
$H=P_{よこ}$
$V_{B}=\frac{P_{たて}e-P_{よこ}d}{f}$
$V_{A}=\frac{P_{たて}(f-e)+P_{よこ}d}{f}$
と求まる。
このように、力のつりあい条件のみから反力(や部材の内力)を 求めることができる構造物を静定構造物という。 これに対して、力のつりあい条件のみからは反力や内力が求まらない 構造物は不静定構造物といい、力と変形の関係や変形と変位の関係を用いないと 反力や内力が求まらない。 構造物の反力の数から力のつりあい式の数を引いた数を 不静定次数と呼ぶ。 つまり、 上の例のような反力の数が3つで、力のつりあい式の数も3つの静定構造物の 不静定次数は0である。 静定梁にヒンジ(回転する節点)をはさみながらローラー支承を 増やしたゲルバー梁の場合、ローラー支承が増えたぶんだけ反力は 増えるが、ヒンジの左側(または右側)でモーメントの合計が0 というつりあい式もそのぶん増えるので、 反力が4つ以上あっても、不静定次数が0であれば 静定構造物となり得る。
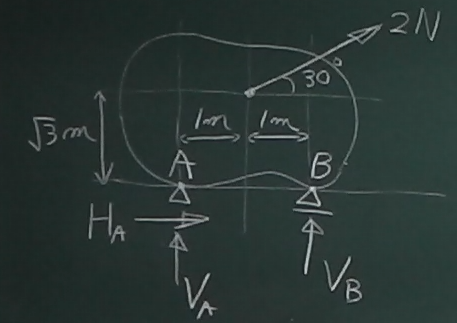 図の支点$A, B$の支点反力を求めてみよう。
図の支点$A, B$の支点反力を求めてみよう。
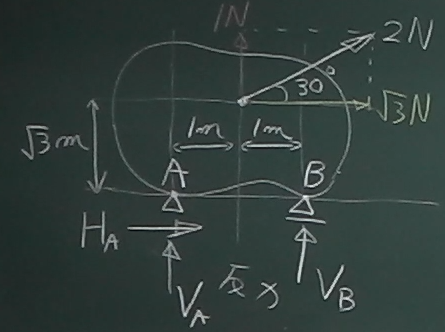 斜め方向の外力は、分解して鉛直方向成分、水平方向成分を求める。
まず、鉛直方向のつりあいを考えてみる。
斜め方向の外力は、分解して鉛直方向成分、水平方向成分を求める。
まず、鉛直方向のつりあいを考えてみる。
$\Sigma\downarrow=-1$N$ -V_{A} -V_{B} =0$
1Nも$V_{A}$も$V_{B}$も全部 上向きだから、下向き正で足し算する場合は、
全部にマイナスがつく。
上向きの力ばっかりだったら、わざわざ下向き正で足し算しなくても、
$\Sigma\uparrow
=1$N$ +V_{A} +V_{B} =0$みたいに上向き正で足し算しても構わない。
1NのNのような単位は、数値だけを計算する場合には、
特に式の中に書かなくて構わないが、
モーメントの計算のように単位どうしをかけたり割ったりする場合には、
次元がわからなくなりやすいので、
様々な次元の数値どうしで計算する場合には、単位も一緒に計算した方が
安全である。
水平方向のつりあいは
$\Sigma\rightarrow=\sqrt{3}$ N$+H_{A}=0$
ここから、$H_{A}=-\sqrt{3}$ Nと求まる。
モーメントのつりあいは、どの点回りに考えてもいいが、
なるべくモーメントを作る力が少ない
(未知数の力でモーメントを作る力が少ない)点の方が計算が楽だ。
今回は点$A$回りでも点$B$回りでも特に違いはないが、点$A$回りで
つりあいを考える。
$\Sigma_{A}$ $=1 $N$ \cdot 1 $m$ -\sqrt{3} $N$ \cdot\sqrt{3} $m$ +V_{B}\cdot 2 $m$ =0$
$=1 $N$ \cdot 1 $m$ -\sqrt{3} $N$ \cdot\sqrt{3} $m$ +V_{B}\cdot 2 $m$ =0$
これを計算すると、$1$ Nm $-3$ Nm $+2V_{B}$ m $=0$
$2V_{B} $ m $=2$ Nm
よって、$V_{B}=1$ Nと求まる。
モーメントの計算の場合は、力(N)と腕の長さ(m)を区別する意味でも、
単位も一緒に計算した方が安全だが、
単位も一緒に計算する場合は、単位のNとかmは、文字変数と同じようにかけたり
わったりしてやればよい。そうすると、自動的に答えに適切な次元
(力なのかモーメントなのか)の単位が導かれる。
ただし、単位も文字変数と同じように計算していいと言うと、
「$V_{B}=2$Nm$/2$m$=$Nよって、$V_{B}=$N」とか答える人がたまにいるが、
答えの数値が1になったからといって、数値部分を省略してはいけない。
$-1$N$ -V_{A} -V_{B} =0$の式に$V_{B}=1N$を代入すれば、
$-1$N$ -V_{A} -1$N$=0$
よって、$V_{A}=-2$N と求まる。
答えの板書は、これ。
その他の例題は、
これ(答え)とか
これ(答え)とか。
2024年度小テスト第1回:
小テスト240426
2020年度小テスト:
問1,
問2,
問3,
解答