
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 前回、変位と変形は違うという話を
した上で、
変位については、初期状態で着目した点が変形後にどこに移動したかを、
変位ベクトルやその成分で表すことにした。
では、変形の方はどうやって表せばいいだろう。
変形を数値で表すには、「ひずみ」という物理量を使う。
伸び縮み変形を表すには、1つの点の変位だけを調べても、
その点がどれだけ動いたかはわかっても、
その点の周囲がどれだけのびたかはわからない。
だから、2つの点の変位を調べて、2つの点の距離が最初の状態から、
のびたか縮んだかで変形の程度を表したい。
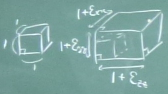
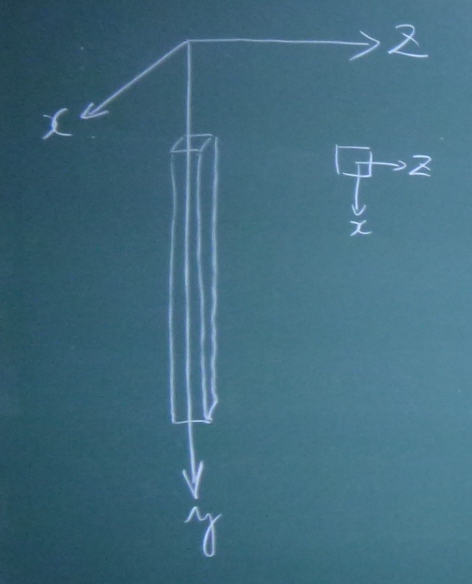
図のように初期状態で$z$軸に横たわる細長い棒があったとして、
その棒の微小部分$dz$に着目する。
初期状態でこの棒の左端が$z$にあるとすると、右端は$z+dz$にあることになる。
さて、この棒が外力を受けて変形しながら変位し、
左端が$z$方向に$w(z)$だけ、右端が$z$方向に$w(z+dz)$だけ変位したとする。
その結果、微小部分$dz$が初期状態よりちょっとだけ伸びたとする。
その初期状態よりちょっとだけ伸びた比率を、
直ひずみ$\varepsilon_{zz}$という量で表したい。
「直ひずみ」は「垂直ひずみ」とも言う。
つまり、伸びる方向の直ひずみを正の$\varepsilon_{zz}$で表すことになるので、
縮む方向の直ひずみは、$\varepsilon_{zz}<0$ということになる。
伸びることを「
前回、変位と変形は違うという話を
した上で、
変位については、初期状態で着目した点が変形後にどこに移動したかを、
変位ベクトルやその成分で表すことにした。
では、変形の方はどうやって表せばいいだろう。
変形を数値で表すには、「ひずみ」という物理量を使う。
伸び縮み変形を表すには、1つの点の変位だけを調べても、
その点がどれだけ動いたかはわかっても、
その点の周囲がどれだけのびたかはわからない。
だから、2つの点の変位を調べて、2つの点の距離が最初の状態から、
のびたか縮んだかで変形の程度を表したい。
図のように初期状態で$z$軸に横たわる細長い棒があったとして、
その棒の微小部分$dz$に着目する。
初期状態でこの棒の左端が$z$にあるとすると、右端は$z+dz$にあることになる。
さて、この棒が外力を受けて変形しながら変位し、
左端が$z$方向に$w(z)$だけ、右端が$z$方向に$w(z+dz)$だけ変位したとする。
その結果、微小部分$dz$が初期状態よりちょっとだけ伸びたとする。
その初期状態よりちょっとだけ伸びた比率を、
直ひずみ$\varepsilon_{zz}$という量で表したい。
「直ひずみ」は「垂直ひずみ」とも言う。
つまり、伸びる方向の直ひずみを正の$\varepsilon_{zz}$で表すことになるので、
縮む方向の直ひずみは、$\varepsilon_{zz}<0$ということになる。
伸びることを「
微小部分$dz$の右端が$w(z+dz)$だけ右に変位して、
左端が$w(z)$だけ右に変位しているから、変形後の微小部分の長さは、
以下のように表せる。
$dz(1+\varepsilon_{zz})=dz+w(z+dz)-w(z)$
これを整理すると、
${\displaystyle \varepsilon_{zz}=\frac{w(z+dz)-w(z)}{dz}
}$
と書けるが、
これは$dz$がじゅうぶんに微小だという仮定のもとでの
ひずみのおおざっぱな定義である。
微小部分の長さ$dz$を極限まで小さくしてやると
これは「微分」の定義になるので、
ある点$z$の
$z$方向の直ひずみは次式のように$z$方向変位の$z$に関する微分として
定義できる。
$
{\displaystyle
\varepsilon_{zz}(z)=\lim_{dz \to 0}\frac{w(z+dz)-w(z)}{dz}
=\frac{d w(z)}{dz}=w'(z)
}
$
 $z$軸に横たわる梁の問題では、
$x$方向や$y$方向の直ひずみは無視できるが、
3次元の物体の変形の問題では、
$x$方向の直ひずみ$\varepsilon_{xx}$や
$y$方向の直ひずみ$\varepsilon_{yy}$も同様に定義できる。
上の棒を太さ(断面)のある梁として捉えるなら、
ここで定義した$\varepsilon_{zz}(z)$は厳密には、
梁の断面の図心位置($x=y=0$)での$z$方向の直ひずみということになる。
下の方の梁モデルのところで少し述べるが、
直ひずみの場合、(変位と違って)
断面の場所によって値が異なることもあるので、厳密には
$\varepsilon_{zz}(x,y,z)$みたいに$x,y,z$に依存する。
$z$軸に横たわる梁の問題では、
$x$方向や$y$方向の直ひずみは無視できるが、
3次元の物体の変形の問題では、
$x$方向の直ひずみ$\varepsilon_{xx}$や
$y$方向の直ひずみ$\varepsilon_{yy}$も同様に定義できる。
上の棒を太さ(断面)のある梁として捉えるなら、
ここで定義した$\varepsilon_{zz}(z)$は厳密には、
梁の断面の図心位置($x=y=0$)での$z$方向の直ひずみということになる。
下の方の梁モデルのところで少し述べるが、
直ひずみの場合、(変位と違って)
断面の場所によって値が異なることもあるので、厳密には
$\varepsilon_{zz}(x,y,z)$みたいに$x,y,z$に依存する。
なお、直ひずみは、伸びた比率だから無次元である。
 せん断変形を数値で表すには
「せん断ひずみ」という物理量を使う。
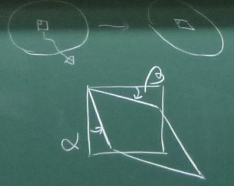
図のように初期状態で長方形だった物体内の微小部分が、
変形後に平行四辺形につぶれた(せん断変形した)とする。
このとき、ある頂点の2辺が内側にそれぞれ角度$\alpha$, $\beta$(ラジアン)だけ
回転して変形したとすると、この平面($yz$面)のせん断ひずみは、
せん断変形を数値で表すには
「せん断ひずみ」という物理量を使う。
図のように初期状態で長方形だった物体内の微小部分が、
変形後に平行四辺形につぶれた(せん断変形した)とする。
このとき、ある頂点の2辺が内側にそれぞれ角度$\alpha$, $\beta$(ラジアン)だけ
回転して変形したとすると、この平面($yz$面)のせん断ひずみは、
せん断ひずみ:
${\displaystyle
\varepsilon_{yz}=\frac{\alpha+\beta}{2}
}$
で表される。
せん断ひずみは、角度(ラジアン)なので、無次元である。
つまり、直ひずみもせん断ひずみも
ひずみは無次元と理解しておけばよい。
補足:
材料や物理の一般の分野で「ひずみ」(英語ではstrain)と言えば、
この無次元量のことを言うのが普通だが、
日本の建築などの分野では、
無次元のひずみの意味では「ひずみ度」という言葉を用いて、
「ひずみ」の方は、長さの次元の伸びの意味で使ったりする習慣もある
(今も?)。
土木やその他の分野では、こうした使い方はまずないと思うが、
「ひずみ度」という表現が出てきたときは、
「ひずみ」が次元のある量で使われている場合があるので注意が必要である。
角度$\alpha$, $\beta$を点の変位から求めるためには、
3つの頂点の変位に着目する必要がある。
梁モデルでは、
断面の図心をつらねた軸の変位($u, v, w$)しか考えないので、
こうした3点の変位とせん断ひずみを関係づけることはしないが、
2次元の物体内の点の変位とせん断ひずみとの関係について、
ちゃんと知りたい場合は、こちらを参照。
なお、$\alpha+\beta$を2で割らずにそのまま「せん断ひずみ」と
呼ぶ場合もあるので注意が必要である。
区別しないと混乱を招くので、2で割らない場合は
「工学的せん断ひずみ」や「工学せん断ひずみ」
と呼ぶ。
工学的せん断ひずみの記号は、$\gamma$が使われることが多いが、
$\varepsilon$が使われることもあるので、
文献中に
せん断ひずみが現れたら、
式中の係数等から2で割ったせん断ひずみか工学せん断ひずみかを判断する
必要がある。
工学せん断ひずみ:
$\gamma_{yz}=\alpha+\beta$
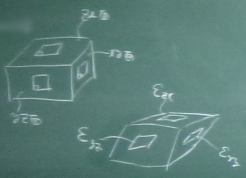 3次元の物体の変形の問題では、
$zx$面のせん断ひずみ$\varepsilon_{zx}$や
$xy$面のせん断ひずみ$\varepsilon_{xy}$も同様に定義できる。
もっとも、細長い梁の問題では、
次項で述べるように、
どのせん断ひずみも無視できる。
3次元の物体の変形の問題では、
$zx$面のせん断ひずみ$\varepsilon_{zx}$や
$xy$面のせん断ひずみ$\varepsilon_{xy}$も同様に定義できる。
もっとも、細長い梁の問題では、
次項で述べるように、
どのせん断ひずみも無視できる。
3次元の物体のひずみは、 直ひずみが $\varepsilon_{xx}$, $\varepsilon_{yy}$, $\varepsilon_{zz}$ の3成分と、 せん断ひずみが $\varepsilon_{xy}$, $\varepsilon_{yz}$, $\varepsilon_{zx}$ の3成分の計6成分あることになる。 が、 次項の梁モデルの仮定で述べるように、 梁モデルで扱うひずみは、これらの中のごく一部なので、 話はだいぶ簡単になるが、 3次元のひずみは、直ひずみ3成分とせん断ひずみ3成分ということは 理解しておく必要がある。
 では、3次元の物体のひずみが直ひずみ:3成分、せん断ひずみ:3成分の
計6成分あることがなんとなくわかったところで、
改めて、梁モデルの仮定をこれらのひずみを用いて、
どう表せるか考えてみる。
では、3次元の物体のひずみが直ひずみ:3成分、せん断ひずみ:3成分の
計6成分あることがなんとなくわかったところで、
改めて、梁モデルの仮定をこれらのひずみを用いて、
どう表せるか考えてみる。
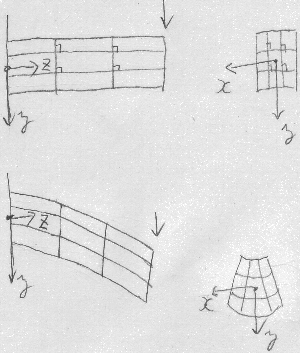
割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形
(せん断ひずみ$\varepsilon_{yz}$)が生じて枡目の角は直角では
なくなるだろう。また棒の断面についても、
例えば引っ張られる上辺は軸方向に伸びたぶん幅方向には縮んだり、
圧縮される下辺は軸方向に縮んだぶん幅方向には膨れたりといった変形も
生じるかも知れない。
これらの変形を考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、それらを考慮すべき場合は、
考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、これらの変形が無視できるような
「非常に細長い棒が、ちょっとだけ曲がる」
場合に限定して考えたい。
という訳で次の2つの仮定を設けることにする。
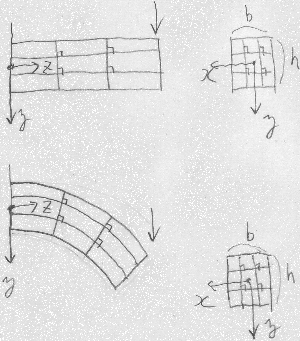
これらの仮定を満たす棒のことをベルヌーイ・オイラー梁 (Bernoulli-Euler梁)とか初等梁と言う。 このテキストで特に注意書きなしで「梁」と書く場合は 初等梁のことを指す。 ちなみに、 ティモシェンコ梁(Timoshenko梁)は、 曲げを受ける平面内のせん断変形を考慮した梁である。
さて、ベルヌーイ・オイラーの仮定と 断面形不変の仮定をすると、ほとんどのひずみ成分は0になってしまい、 考えなくてよい。 0でないひずみは、軸方向の直ひずみ$\varepsilon_{zz}$だけである。 つまり、 初等梁では、ひずみとして、 $\varepsilon_{zz}$だけを扱えばいい ので、 だいぶ、話が簡単になる。 それにしても、梁(の断面の各点)は軸方向にしか伸び縮みしないのに、 それで梁がたわむ(曲がる)のを表現できるのだろうか。 それについては、次回以降、考えていく。
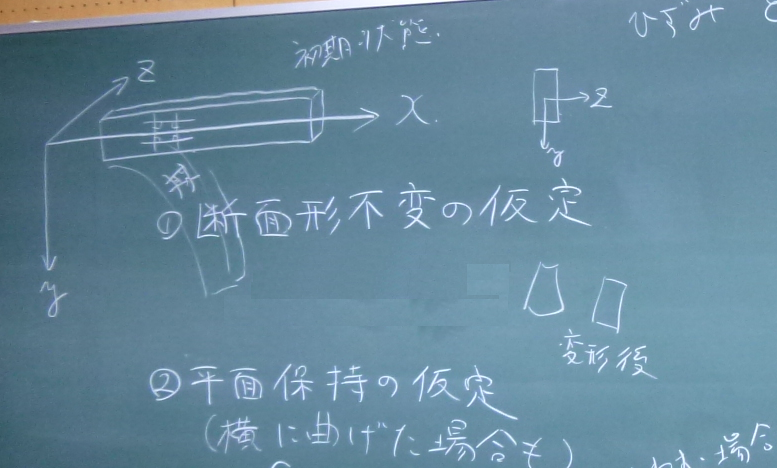
 図のように細長い棒が$y$軸に横たわっているとき、
この棒が梁モデルと見なせるための
ベルヌーイ・オイラーの仮定(平面保持の仮定)と
断面形不変の仮定を
ひずみ成分($\varepsilon_{xx}$,
$\varepsilon_{yy}$,
$\varepsilon_{zz}$,
$\varepsilon_{xy}$,
$\varepsilon_{yz}$,
$\varepsilon_{zx}$)を用いて表わせ。
答えはここ。
図のように細長い棒が$y$軸に横たわっているとき、
この棒が梁モデルと見なせるための
ベルヌーイ・オイラーの仮定(平面保持の仮定)と
断面形不変の仮定を
ひずみ成分($\varepsilon_{xx}$,
$\varepsilon_{yy}$,
$\varepsilon_{zz}$,
$\varepsilon_{xy}$,
$\varepsilon_{yz}$,
$\varepsilon_{zx}$)を用いて表わせ。
答えはここ。
 図のように細長い棒が$x$軸に横たわっているとき、
この棒が梁モデルと見なせるための
ベルヌーイ・オイラーの仮定(平面保持の仮定)と
断面形不変の仮定を
ひずみ成分($\varepsilon_{xx}$,
$\varepsilon_{yy}$,
$\varepsilon_{zz}$,
$\varepsilon_{xy}$,
$\varepsilon_{yz}$,
$\varepsilon_{zx}$)を用いて表わせ。
答えはここ。
図のように細長い棒が$x$軸に横たわっているとき、
この棒が梁モデルと見なせるための
ベルヌーイ・オイラーの仮定(平面保持の仮定)と
断面形不変の仮定を
ひずみ成分($\varepsilon_{xx}$,
$\varepsilon_{yy}$,
$\varepsilon_{zz}$,
$\varepsilon_{xy}$,
$\varepsilon_{yz}$,
$\varepsilon_{zx}$)を用いて表わせ。
答えはここ。
 図のように初期状態で$x$軸に横たわる棒の微小部分$dx$が、
変形後に左端が$u(x)$, 右端が$u(x+dx)$だけ変位したとする。
図のように初期状態で$x$軸に横たわる棒の微小部分$dx$が、
変形後に左端が$u(x)$, 右端が$u(x+dx)$だけ変位したとする。
①変形後の長さ$dx+\Delta=$
②$\frac{のび}{もとの長さ}=\frac{\Delta}{dx}=$
③$dx\rightarrow 0$の極限をとり、$\varepsilon_{xx}(x)$を求めよ
答えはここ。
動画の解説は第2回 例題。
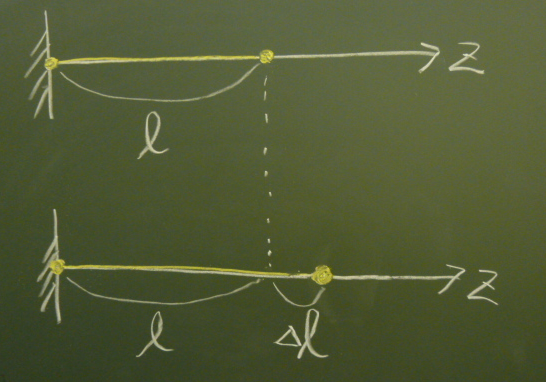 図のように初期状態で$z$軸に長さ$\ell$の棒が横たわっている。
この棒の左端が$z$軸の原点に固定されており、
右端を右方向に引っ張ったところ、
図のように棒が$\Delta\ell$だけ伸びたとする。
このとき、変形後の棒の$z$方向変位を(初期状態の$z$の関数として)
$w(z)=az+b$のような線形の1次式で表したい。
$w(0)$と$w(\ell)$を求め、
$w(z)$を求めよ。
また、
$\varepsilon_{zz}(z)$を求めよ。
図のように初期状態で$z$軸に長さ$\ell$の棒が横たわっている。
この棒の左端が$z$軸の原点に固定されており、
右端を右方向に引っ張ったところ、
図のように棒が$\Delta\ell$だけ伸びたとする。
このとき、変形後の棒の$z$方向変位を(初期状態の$z$の関数として)
$w(z)=az+b$のような線形の1次式で表したい。
$w(0)$と$w(\ell)$を求め、
$w(z)$を求めよ。
また、
$\varepsilon_{zz}(z)$を求めよ。
答え
左端は固定されていて変位は0だから、$w(0)=b=0$
右端は初期状態から$z$の正方向に$\Delta\ell$ だけ変位しているから、
$w(\ell)=a\ell+b=a\ell=\Delta\ell$ よって、$a=\frac{\Delta\ell}{\ell}$
よって、$w(z)=\frac{\Delta\ell}{\ell}z$
$\varepsilon_{zz}(z)=w'(z)=\frac{\Delta\ell}{\ell}$
注意:第1回で述べたように、
変位関数$w(z)$は、初期状態での点の座標$z$の関数である。
つまり、初期状態で$z$にあった点が、変形後に、初期状態での座標から
どれだけ変位したかを表している。
変形後の点の座標の関数ではない。
2022年度小テスト:
小テスト221019
2021年度小テスト:
問,
解答
2020年度小テスト:
問1,
問2,
解答
メモ: