
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
構造力学Iでは、 静定構造(トラスや梁)に外力が加わったとき、 その反力や内力(部材力、断面力)がどうなるかというのを、 主に力のつりあいから求める方法を学んだ。 構造物を作る際、ものが壊れないように作るには、物体内部に発生している内力を 知ることは重要だ。 一方で、構造物(例えば橋)が、その機能を果たすためには、 壊れないだけでは不十分で、 例えば、車や電車が橋を通ると、橋はある程度は変形する(たわむ)が、 壊れさえしなければ、いくら変形してもいいということにはならない。 構造物の変形は、構造物を安全に使用できる範囲に収まらなければならない。 ということで、構造物が外力を受けた場合の内力の情報だけでなく、 変形についての情報(任意点の変位とか)を求めるためのスキルを学ぶのが、 構造力学(応用)である。
「変位」というのは、着目している点がどこに移動したかということで、 「変形」というのは、着目している物体の形が変わること。 物体の形がほとんど変形せずに、遠くまで変位することもあれば、 物体がある場所に留まってぐしゃっと大きく変形することもある。 つまり、「変位」と「変形」は違う。 この点が横の方にすごく変位したとか、 この棒がぐにゃっとすごく変形したとかいうのを 数値(とか座標の関数とか)で表すにはどうしたらいいだろう。
 構造力学Iと同様に、
座標は、梁軸方向に$z$, たわみ方向に$y$を取る。
二次元の梁の問題は黒板を$yz$平面として考える。
構造力学Iと同様に、
座標は、梁軸方向に$z$, たわみ方向に$y$を取る。
二次元の梁の問題は黒板を$yz$平面として考える。
 物体が外力を受けずに変位も変形もせずに静止している状態を
初期状態と呼ぶことにする。
初期状態にあった物体が、外力を受けるなどして変位し変形した状態を
変形状態とか変形後と呼ぶことにする。
さて、
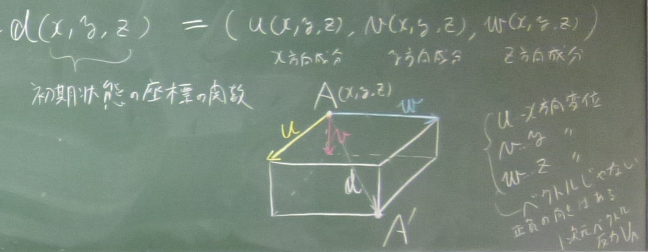
初期状態で点$A(x,y,z)$にあった物体内の点が、外力を受けるなどして、
変形後に
図のように、
$x$方向に$u$だけ,
$y$方向に$v$だけ,
$z$方向に$w$だけそれぞれ変位して、点$A'(x',y',z')$まで移動したとする。
我々は、初期状態である座標$(x,y,z)$にあった点が、外力を受けて変形した後に、
どこに移動したかということを知りたいので、
これらの変位を、それぞれ初期状態の座標$(x,y,z)$の関数として、
$u(x,y,z), v(x,y,z), w(x,y,z)$のように表すことにする。
$x$方向変位$u$は、$u(x)$のように、$x$にしか依存しないように思った人もいるだろうか。
初期状態で$x$座標が同じ点だからといって、$x$方向に同じ変位になるとは限らない。
例えば、図の$y$軸上にある点は、$x=0$で$x$座標は同じだが、
$y$の位置によって$x$方向変位が違ったっていい。
例えば、
$y=0$の近くでは$x$方向にほとんど変位しておらず、$u(x=0, y=0)=0$なのに対して、
$y$が大きくなるにつれて$x$方向の変位が増えてきて、
$y=10$の辺りでは、$u(x=0, y=10)=3$とかいうこともある。
物体が外力を受けずに変位も変形もせずに静止している状態を
初期状態と呼ぶことにする。
初期状態にあった物体が、外力を受けるなどして変位し変形した状態を
変形状態とか変形後と呼ぶことにする。
さて、
初期状態で点$A(x,y,z)$にあった物体内の点が、外力を受けるなどして、
変形後に
図のように、
$x$方向に$u$だけ,
$y$方向に$v$だけ,
$z$方向に$w$だけそれぞれ変位して、点$A'(x',y',z')$まで移動したとする。
我々は、初期状態である座標$(x,y,z)$にあった点が、外力を受けて変形した後に、
どこに移動したかということを知りたいので、
これらの変位を、それぞれ初期状態の座標$(x,y,z)$の関数として、
$u(x,y,z), v(x,y,z), w(x,y,z)$のように表すことにする。
$x$方向変位$u$は、$u(x)$のように、$x$にしか依存しないように思った人もいるだろうか。
初期状態で$x$座標が同じ点だからといって、$x$方向に同じ変位になるとは限らない。
例えば、図の$y$軸上にある点は、$x=0$で$x$座標は同じだが、
$y$の位置によって$x$方向変位が違ったっていい。
例えば、
$y=0$の近くでは$x$方向にほとんど変位しておらず、$u(x=0, y=0)=0$なのに対して、
$y$が大きくなるにつれて$x$方向の変位が増えてきて、
$y=10$の辺りでは、$u(x=0, y=10)=3$とかいうこともある。
$u(x,y,z), v(x,y,z), w(x,y,z)$を用いて
点$A$の変位をベクトルとして、
$\mathbf{d}(x,y,z)=(u(x,y,z),v(x,y,z),w(x,y,z))$と表したものを
点$A$の変位ベクトルと言う。
これは初期状態での点$A$の座標$(x,y,z)$の関数になっている。
つまり、初期状態で$(x,y,z)$にあった点$A$が、変形後に初期状態での$(x,y,z)$
からどの方向にどれだけ移動したかを
表しているのが点$A$の変位ベクトルである。ただし、
ベクトルの成分$u,v,w$
(それぞれ$x$方向変位、$y$方向変位、$z$方向変位)は、方向が決まっているので、
ベクトルではない。
方向が決まっていて正負の区別がある
1次元ベクトルとして扱う
(反力$V_{A}$とかの扱いと同じ)。
脱線:
私は修士論文で、「対象物体のある初期状態を」と書いたものを、
先生から「対象物体のある処女状態を」と直されたことがある。
まあ、1991年頃の話で、当時、24才ぐらいの私は、
自分の修士論文にそんな言葉を書かなければならないのが、なんともいやだった。
まあ、構造系の場合、
こうした性的なたとえを用いた用語は、あまりないのだが、
分野によっては、「処女載荷」みたいな用語がまだ残ってたりするかもしれない。
このような性的なたとえを用いた科学用語は、
土木分野に限らず、
日本語に限らず(というか日本語はたいてい英語をそのまま訳したものだが)、
英語でもたくさんあり
(処女彗星とか。
まあ、科学用語に限らず「処女作」みたいな表現もまだまだ使われているが)、
性的なたとえを使わない表現への言い換えが少しずつなされているのではないだろうか。
最近の分野ごとの状況を調べてみたい
(さすがに、初年次ゼミの調査ネタにするのは、あまりふさわしくないだろうか。
社会学を学ぶ学生だったら、格好のテーマなのかもしれないが...)。
あと、私がよく使いたいけど躊躇する言葉として、「紳士協定」というのがあるが、
これも性的に中立でない言葉だ。
何かいい言い換えがないかとネットで検索しても、まだ良さそうなのはヒットしない。
意味的には「善意の協定」とかで言い換えにならないだろうか。
 「梁モデル」というのは、いくつかの仮定をした梁のモデルだが、
どんな仮定かについては、
次回で
後述する。
今のところ、構造力学Iでやったような
$z$軸に横たわる棒ということでいい。
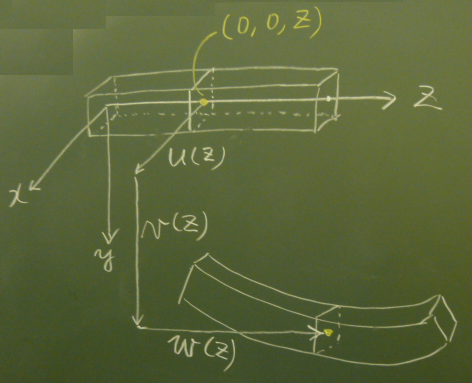
梁モデルの場合、断面の図心(重心)をつらねた線を$z$軸にとる。
すると、断面($xy$平面)の図心の座標は$(0,0,z)$で表される。
梁モデルと見なせる梁は、梁の長さに比べて断面が十分に小さいため、
ある断面内の$x,y$座標が違う点の変位は、
その断面の図心の変位とほぼ同じなので、
梁のある断面の変位は、図心の変位で代表させて扱う。
ある断面の図心の$x, y, z$方向変位は、
$u(0,0,z), v(0,0,z), w(0,0,z)$と書けるが、$x$と$y$は常に0だから、
以下のように$z$だけの関数として扱う。
図心というのは、密度が一定の場合の重心のことで、密度が関係しないから、
長方形は真ん中とか、三角形は底辺から$\frac{1}{3}$とか図形的に決まる。
重心というのは、その点で吊るすとモーメントがつりあう点だが、密度のばらつきがあると図心とは
一致しない。
「梁モデル」というのは、いくつかの仮定をした梁のモデルだが、
どんな仮定かについては、
次回で
後述する。
今のところ、構造力学Iでやったような
$z$軸に横たわる棒ということでいい。
梁モデルの場合、断面の図心(重心)をつらねた線を$z$軸にとる。
すると、断面($xy$平面)の図心の座標は$(0,0,z)$で表される。
梁モデルと見なせる梁は、梁の長さに比べて断面が十分に小さいため、
ある断面内の$x,y$座標が違う点の変位は、
その断面の図心の変位とほぼ同じなので、
梁のある断面の変位は、図心の変位で代表させて扱う。
ある断面の図心の$x, y, z$方向変位は、
$u(0,0,z), v(0,0,z), w(0,0,z)$と書けるが、$x$と$y$は常に0だから、
以下のように$z$だけの関数として扱う。
図心というのは、密度が一定の場合の重心のことで、密度が関係しないから、
長方形は真ん中とか、三角形は底辺から$\frac{1}{3}$とか図形的に決まる。
重心というのは、その点で吊るすとモーメントがつりあう点だが、密度のばらつきがあると図心とは
一致しない。
$u(z)$ 横たわみ
$v(z)$ たわみ
$w(z)$ 軸方向変位
梁では、一般に最も大きい変位は下($y$)方向変位$v(z)$で、下方向変位のことを「たわみ」
と言う。
また、下方向に変位することを「たわむ」と言う。
2次元の問題では梁が$yz$平面から飛び出すことは考えないが、
3次元の問題の場合、梁が横から荷重を受けて、横($x$)方向にも変位する。
横方向変位$u(x)$のことを「横たわみ」と言う。
梁は、たわみに比べると軸方向にはあまり変位しないが、軸($z$)方向の変位$w(z)$は、そのまま軸方向変位と
言っておく。
「たわむ」とか「たわみ」という言葉を日常で使ってない人もいるかもしれないが、
日常語では、「枝がたわむ」とか「床がたわむ」と使う。まあ、「しなう」に近いか。
構造力学Iでは、静定梁が外力を受けた場合の内力(断面力)を、 $S(z)$や$M(z)$など、$z$の関数として求めたが、 構造力学(応用)では、静定梁や不静定梁のたわみ$v(z)$を$z$の関数として 求める方法を学ぶことが1つの目的である。これができると、 不静定梁の断面力も求められる。
 変形には「伸び縮み変形」と「せん断変形」がある。
まず、
物体の中に各辺が座標軸と平行な微小な立方体(2次元なら正方形)の要素を
考えて、その四角い要素がどのように変形するかということに
着目してみる。
簡単のため2次元で考えるとして、
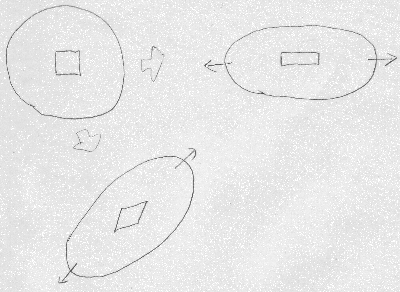
例えば、図のような物体が左右に引っ張られたとして、
微小正方形要素の周辺が$z$軸方向には一様に伸び、
$y$方向には一様に縮んだとすると、
正方形要素は、頂点の直角を保ったまま長方形に変形する。
このように、物体中の微小な立方体(2次元なら正方形)要素が、
頂点の直角を保ちながら、直方体(2次元なら長方形)に変形するような変形を、
ここでは「伸び縮み変形」と呼んでおく。
一方、図のような物体を微小正方形の対角線方向に斜めに引っ張ったら、
微小正方形要素は、頂点の直角がくずれて、ひし形に変形するだろう。
このように物体中の微小な立方体(2次元なら正方形)要素が、
(辺の長さは変えずに)頂点の角度を変えるような変形を「せん断変形」と呼ぶ。
すると、これ以外の一般的な変形
(図の微小正方形が不等辺の平行四辺形になるような)も、
「伸び縮み変形」と「せん断変形」の組合せとして表せそうだ。
変形には「伸び縮み変形」と「せん断変形」がある。
まず、
物体の中に各辺が座標軸と平行な微小な立方体(2次元なら正方形)の要素を
考えて、その四角い要素がどのように変形するかということに
着目してみる。
簡単のため2次元で考えるとして、
例えば、図のような物体が左右に引っ張られたとして、
微小正方形要素の周辺が$z$軸方向には一様に伸び、
$y$方向には一様に縮んだとすると、
正方形要素は、頂点の直角を保ったまま長方形に変形する。
このように、物体中の微小な立方体(2次元なら正方形)要素が、
頂点の直角を保ちながら、直方体(2次元なら長方形)に変形するような変形を、
ここでは「伸び縮み変形」と呼んでおく。
一方、図のような物体を微小正方形の対角線方向に斜めに引っ張ったら、
微小正方形要素は、頂点の直角がくずれて、ひし形に変形するだろう。
このように物体中の微小な立方体(2次元なら正方形)要素が、
(辺の長さは変えずに)頂点の角度を変えるような変形を「せん断変形」と呼ぶ。
すると、これ以外の一般的な変形
(図の微小正方形が不等辺の平行四辺形になるような)も、
「伸び縮み変形」と「せん断変形」の組合せとして表せそうだ。
上の例では、微小正方形要素の各辺が座標軸と平行になるような要素を
考えることにしたが、もし微小正方形要素を45°回転させたら、
今度は、左右に引っ張るとせん断変形して、
右上と左下の斜め方向に引っ張ると伸び縮み変形するようにもできる。
つまり、伸び縮み変形とかせん断変形というのは、
どの座標系で観測するかに依存して変わってくるものであるし、
逆に言うと、どんな変形状態でも伸び縮み変形として捉えることのできる
向きがあることになる(この辺の話は「主ひずみ」
や「主応力」の話をする機会が
あれば後述)。
 図のような梁モデルの左端の
点Aの$x, y, z$方向変位$u(z), v(z), w(z)$を図示せよ。
答えは、
ここ。
図のような梁モデルの左端の
点Aの$x, y, z$方向変位$u(z), v(z), w(z)$を図示せよ。
答えは、
ここ。
「直ひずみ」と「せん断ひずみ」の違いについて、簡単に説明せよ。 図を用いてもよい。 解答例は、ここ。
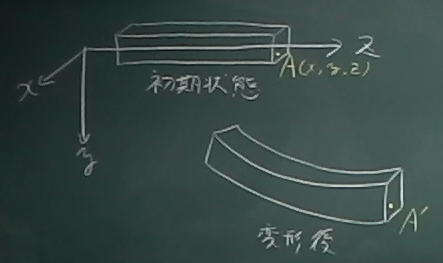
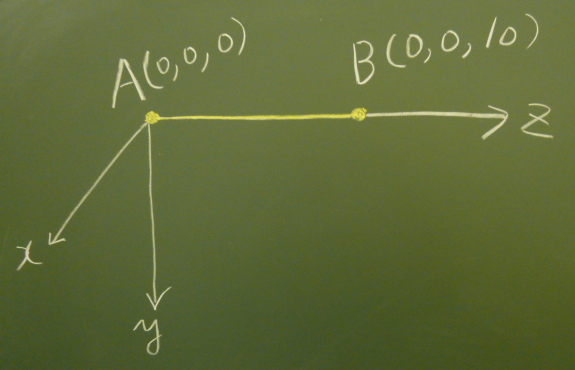 図のように線分と見なせる梁ABが初期状態で$z$軸上に横たわっていて、
点Aの座標は$(0,0,0)$, 点Bの座標は$0,0,10)$である。
今、梁ABが外力を受けて変形し、
変形後の$x, y, z$方向変位が、それぞれ
図のように線分と見なせる梁ABが初期状態で$z$軸上に横たわっていて、
点Aの座標は$(0,0,0)$, 点Bの座標は$0,0,10)$である。
今、梁ABが外力を受けて変形し、
変形後の$x, y, z$方向変位が、それぞれ
$u(z)=5$
$v(z)=z+6$
$w(z)=0$
で表されるとする。
変形後の点A(点A')、変形後の点B(点B')の座標を求め、
変形後の梁ABの概形を描け。
答えは、
ここ。
ちなみに、梁の断面のある点Cの座標が、
初期状態で
$(x_{c}, y_{c}, z_{c})$であるとき、
変形後の点Cの座標は、
$(x_{c}+u(z_{c}), y_{c}+v(z_{c}), z_{c}+w(z_{c}))$で表される。
今回、
点Aの$z$座標は0だから、点Aの変位は、
$u(0)=5, v(0)=6, w(0)=0$. これらを初期状態での点Aの座標$(0,0,0)$に
足してやれば、点A'は$(5,6,0)$となる。
一方、
点Bの$z$座標は10だから、点Bの変位は、
$u(10)=5, v(10)=16, w(10)=0$. これらを初期状態での点Bの座標$(0,0,10)$に
足してやれば、点B'は$(5,16,10)$となる。
2022年度小テスト:
小テスト221012
2021年度小テスト:
問1,
解答
2020年度小テスト:問,
解答
メモ: