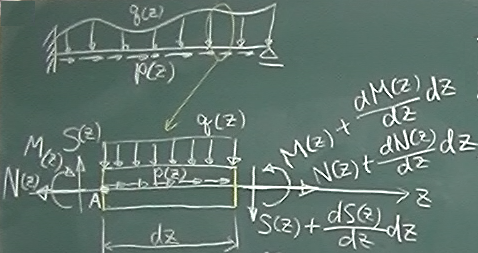
 任意の境界条件で任意の外力を受けてつりあっている梁の微小部分を切り取って、
この微小部分の力のつりあいを考えてみる。
任意の境界条件で任意の外力を受けてつりあっている梁の微小部分を切り取って、
この微小部分の力のつりあいを考えてみる。
注意: このページの数式は、 MathJaxを使って書いてます。 数式部分がおかしい場合は、更新ボタンをクリックすると 改善するかも知れません。 太文字のギリシャ文字($\mathbf{\sigma}$など)が、 太文字になっていない($\sigma$)かもしれません。 印刷版で確認して下さい。 その他、おかしい記述があると思ったら、 メールなどで指摘して下さい。
 任意の境界条件で任意の外力を受けてつりあっている梁の微小部分を切り取って、
この微小部分の力のつりあいを考えてみる。
任意の境界条件で任意の外力を受けてつりあっている梁の微小部分を切り取って、
この微小部分の力のつりあいを考えてみる。
微小部分の長さは$dz$とし、
この微小範囲では鉛直方向の分布荷重外力$q(z)$や
軸方向の分布荷重外力$p(z)$は等分布していると見なせることにしておく。
切り取られたことによってできた両端の切断面には、
この切り取られた部分だけでつりあいが成り立つような
内力としての断面力が
図心($z$軸)に作用していることにする。
この微小部分は外力を受けているので、
左端の断面力と右端の断面力は大きさが同じ(で向きが逆)にはならない。
左端での軸力を$N(z)$, せん断力を$S(z)$, 曲げモーメントを$M(z)$とすると、
そこから$dz$だけずれた右端での断面力は
(応力のつりあいの節の考え方と同様に)、
それぞれ
$N(z)+\frac{dN(z)}{dz}dz$,
$S(z)+\frac{dS(z)}{dz}dz$,
$M(z)+\frac{dM(z)}{dz}dz$
と表せる。これらを用いてこの微小部分の力のつりあいを考えると
$y$方向の力のつりあい(下+):
$-S(z)+q(z)dz+(S(z)+\frac{dS(z)}{dz}dz)=0$
$z$方向の力のつりあい(右+):
$-N(z)+p(z)dz+(N(z)+\frac{dN(z)}{dz}dz)=0$
$A$点左まわりのモーメントのつりあい:
$-M(z)-q(z)dz\frac{dz}{2}-(S(z)+\frac{dS(z)}{dz}dz)dz
+(M(z)+\frac{dM(z)}{dz}dz)
=0$
となる。
$q(z)dz\frac{dz}{2}$や$(\frac{dS(z)}{dz}dz)dz$
は$d$のつく微小量の2次項なので微小と見なして無視して整理すると、
$S(z)=
\frac{dM(z)}{dz}$
(重要)
となり、せん断力が曲げモーメントの微分であるという関係式が得られる。
また、
$y$方向のつりあい式を整理すると:
$\frac{dS(z)}{dz}+q(z)=0$
となるが、これに上のせん断力と曲げモーメントの関係
を代入すると、曲げに関するつりあい式は、
$\frac{d^{2}M(z)}{dz^{2}}+q(z)=0$
となる。また、$z$方向のつりあい式を整理すると、
軸力のつりあい式が
$\frac{dN(z)}{dz}+p(z)=0$
となる。
梁モデルの仮定の仮定では、
初等梁にはせん断変形がないことになっていた。
だから、初等梁でゼロでないひずみは、
軸方向の伸びひずみ$\epsilon_{zz}$だけで、
ゼロでない応力は
軸方向の直応力$\sigma_{zz}$だけであった。
だから、この軸方向の直応力$\sigma_{zz}$を面積積分して合計することによって
合応力としての
軸力$N$を定義したり、
この軸方向の直応力$\sigma_{zz}$に「腕の長さ」をかけながら
面積積分して合計する
ことによって
合応力としての
曲げモーメント$M$
を定義することはできたが、
断面に作用するせん断応力$\sigma_{yz}$はない(無視できる)ことになっていたので、
合応力としての
せん断力$S$を定義することはできなかった。
それなのに梁の微小部分の分布外力と断面力の力のつりあいを考えると、
(断面に作用するせん断応力$\sigma_{yz}$は無視されているにもかかわらず)
せん断力が、曲げモーメントの微分として
$S(z)=\frac{dM(z)}{dz}$
と与えられてしまう。これは
梁モデルの仮定
(でやや強引な仮定をしたことによる)
初等梁理論のちょっと変な点である。
そもそも、断面のせん断応力$\sigma_{yz}$が無視できるからといって、
断面のせん断力$S$もないことにしてしまうと、
力のつりあいは曲げモーメントが一定の場合しかなりたたなくなってしまう。
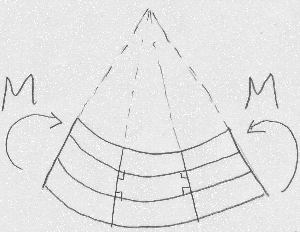 実はベルヌーイ・オイラーの仮定が
(それほど細長くない梁にも一般的に)成り立つ変形は、
梁が円弧のように変形する場合で、これは曲げモーメントが一定
の状態で「純曲げ」と呼ばれる状態である。
しかし、初等梁理論では純曲げ状態でなくても
ベルヌーイ・オイラーの仮定が
成り立つことにしてしまったために、
「断面のせん断応力$\sigma_{yz}$は無視できても、
断面力としてのせん断力$S$はあることにしないとモーメントのつりあいが
満たされない」
という矛盾点を抱える理論なので、その点に注意しておく必要がある。
実はベルヌーイ・オイラーの仮定が
(それほど細長くない梁にも一般的に)成り立つ変形は、
梁が円弧のように変形する場合で、これは曲げモーメントが一定
の状態で「純曲げ」と呼ばれる状態である。
しかし、初等梁理論では純曲げ状態でなくても
ベルヌーイ・オイラーの仮定が
成り立つことにしてしまったために、
「断面のせん断応力$\sigma_{yz}$は無視できても、
断面力としてのせん断力$S$はあることにしないとモーメントのつりあいが
満たされない」
という矛盾点を抱える理論なので、その点に注意しておく必要がある。
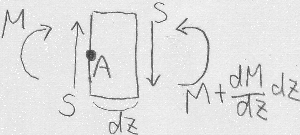 例えば、図のように微小部分の左端と右端とで曲げモーメントが異なる場合、
$A$点まわりのモーメントのつりあいは、$\frac{dM}{dz}dz-Sdz=0$となり、
つまり
$S(z)=\frac{dM(z)}{dz}$
となる訳だが、$S=0$にしてしまうと、
モーメントの変化率$\frac{dM(z)}{dz}$も0になってしまうので、
純曲げしか表せなくなってしまう。
いくら細長くてせん断変形が無視できる梁だからといって、
断面力は純曲げ状態にしかならないというモデルでは、
精度が悪すぎて実用的ではないだろう。
そこで、(せん断応力$\sigma_{yz}$は無視できたとしても)
モーメントのつりあいを満たすために必要なせん断力$S$を
モーメントの変化率として
$S(z)=\frac{dM(z)}{dz}$
と定義してやることで、細長い梁に対する実用的な
予測が行えるモデルとなっているのである。
例えば、図のように微小部分の左端と右端とで曲げモーメントが異なる場合、
$A$点まわりのモーメントのつりあいは、$\frac{dM}{dz}dz-Sdz=0$となり、
つまり
$S(z)=\frac{dM(z)}{dz}$
となる訳だが、$S=0$にしてしまうと、
モーメントの変化率$\frac{dM(z)}{dz}$も0になってしまうので、
純曲げしか表せなくなってしまう。
いくら細長くてせん断変形が無視できる梁だからといって、
断面力は純曲げ状態にしかならないというモデルでは、
精度が悪すぎて実用的ではないだろう。
そこで、(せん断応力$\sigma_{yz}$は無視できたとしても)
モーメントのつりあいを満たすために必要なせん断力$S$を
モーメントの変化率として
$S(z)=\frac{dM(z)}{dz}$
と定義してやることで、細長い梁に対する実用的な
予測が行えるモデルとなっているのである。
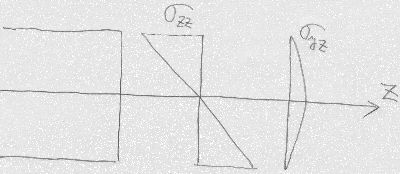 さて、初等梁の式を導く際には、せん断応力$\sigma_{yz}$を無視しているが、
実際には、細長い梁でもせん断応力はそれなりにあるのである。
初等梁の
直応力$\sigma_{zz}$は、三角形分布しているが、
この直応力とつりあうようなせん断応力を求めると、
せん断応力$\sigma_{yz}$は、図のような放物線分布をしていて、
$y=0$の位置で最大となる。
ちなみに、長方形断面の場合、断面の最大せん断応力は、
$\sigma_{yz}^{max}=\frac{3S}{2A}$となる。
こうしたせん断応力に関する詳しい解説は、
このテキストのネタ本でもある
岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛--
計算機による構造解析の基礎としての構造力学を独習する』
を参照してほしい。
さて、初等梁の式を導く際には、せん断応力$\sigma_{yz}$を無視しているが、
実際には、細長い梁でもせん断応力はそれなりにあるのである。
初等梁の
直応力$\sigma_{zz}$は、三角形分布しているが、
この直応力とつりあうようなせん断応力を求めると、
せん断応力$\sigma_{yz}$は、図のような放物線分布をしていて、
$y=0$の位置で最大となる。
ちなみに、長方形断面の場合、断面の最大せん断応力は、
$\sigma_{yz}^{max}=\frac{3S}{2A}$となる。
こうしたせん断応力に関する詳しい解説は、
このテキストのネタ本でもある
岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛--
計算機による構造解析の基礎としての構造力学を独習する』
を参照してほしい。
さて、上で導いた
軸力に関するつりあい式
$\frac{dN(z)}{dz}+p(z)=0$
と
曲げに関するつりあい式
$\frac{d^{2}M(z)}{dz^{2}}+q(z)=0$
に、
軸力-図心変位関係
$N(z)=EA\frac{d w(z)}{dz}$
と
曲げモーメント-たわみ関係
$M(z)=
-EI\frac{d^{2}v(z)}{dz^{2}}$
をそれぞれ代入すると
$EA\frac{d^{2}w(z)}{dz^{2}}+p(z)=0$
$-EI\frac{d^{4}v(z)}{dz^{4}}+q(z)=0$
(最重要)
のような図心変位$v$(たわみ)と$w$(軸方向変位)の微分方程式が導かれる。
これを梁の支配(微分)方程式とか、
特にたわみに関する式をたわみの微分方程式とか言う。
これらの式を積分して、
静定梁のたわみの境界値問題の解法と
同じ要領で境界条件と連続条件
(と後述するが、集中荷重の場合は載荷点の微小部分の外力と断面力のつりあい条件)を
使って積分定数を決定すれば、
不静定梁のたわみや軸方向変位を求めることができる。
梁の微分方程式を積分して、 たわみや断面力などを求める際、 たわみ$v$の微分($v', v'', v'''$など)がたわみ角や断面力と どのように関係付けられているかということを知っていないと、 境界条件や連続条件などを適切に利用することができない。 そこで、以下にたわみの微分とたわみ角や断面力との関係式をまとめておく。
メモ: