
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
第1回の「はじめに」で、
 構造力学(応用)の目的は、構造物が外力を受けたときの内力の情報だけではなく、
変形についての情報(任意点の変位)とかを求めるスキルを学ぶのが
目的だと言った。
今、梁の変形については、
第3回で、
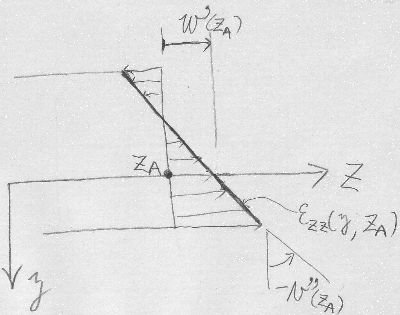
断面に軸($z$)方向の直ひずみが、
$\varepsilon_{zz}(y,z)=w'(z)-yv''(z)$の三角形分布をしているという
ところまで、導いた。
このひずみの式は、軸方向変位$w(z)$やたわみ$v(z)$で表されているから、
ひずみと外力の関係がわかれば、こうした変位も求められるかもしれない。
しかし、ひずみと外力をいきなり関係づけるのは難しい。
というのは、例えば、ひずみの分布は断面で三角形分布してたりして、
梁の内部の場所によって値が異なる。
構造力学(応用)の目的は、構造物が外力を受けたときの内力の情報だけではなく、
変形についての情報(任意点の変位)とかを求めるスキルを学ぶのが
目的だと言った。
今、梁の変形については、
第3回で、
断面に軸($z$)方向の直ひずみが、
$\varepsilon_{zz}(y,z)=w'(z)-yv''(z)$の三角形分布をしているという
ところまで、導いた。
このひずみの式は、軸方向変位$w(z)$やたわみ$v(z)$で表されているから、
ひずみと外力の関係がわかれば、こうした変位も求められるかもしれない。
しかし、ひずみと外力をいきなり関係づけるのは難しい。
というのは、例えば、ひずみの分布は断面で三角形分布してたりして、
梁の内部の場所によって値が異なる。
 梁が、ある外力を受けたときに内部でどのように力が分布しているかというと、
構造力学Iの第5回によると、
梁の断面に軸力$N$とせん断力$S$と曲げモーメント$M$が作用することになっていた。
でも、これらの断面力とひずみの三角形分布とを関係づける方法が
思いつくだろうか。
だって、ひずみは三角形分布していて高さ$y$についての関数になっているのに、
$N, S, M$は、断面の高さ方向の位置に関係なく、ある断面($z=z_{A}$)では
それぞれ1つの値だ。それについて、
構造力学Iの第5回でも小さい字で
以下のような
補足説明が書かれていた。
梁が、ある外力を受けたときに内部でどのように力が分布しているかというと、
構造力学Iの第5回によると、
梁の断面に軸力$N$とせん断力$S$と曲げモーメント$M$が作用することになっていた。
でも、これらの断面力とひずみの三角形分布とを関係づける方法が
思いつくだろうか。
だって、ひずみは三角形分布していて高さ$y$についての関数になっているのに、
$N, S, M$は、断面の高さ方向の位置に関係なく、ある断面($z=z_{A}$)では
それぞれ1つの値だ。それについて、
構造力学Iの第5回でも小さい字で
以下のような
補足説明が書かれていた。
構造力学(応用)でやるが、 実際には、梁の切断面には「応力」という内力が分布しているが、 梁モデルでは、これらの内力を 1点に作用する以下の3つの力にまとめて扱うということ。
つまり、そういうことだ。 梁の断面には、「応力」という内力が分布しているのを、 梁モデルでは、その応力の分布を、断面の図心に作用する3つの断面力$N, S, M$に まとめてしまったということだ。 ひずみの三角形分布を断面の内力と関係づけようとするなら、 断面に分布している応力と関係づけるべきではないだろうか。 というわけで、以下に「応力」の説明をしていこうと思う。 コンクリや土質、水理などの授業で既に「応力」が登場していると話が早いが、 一応、以下に最低限の説明をする。
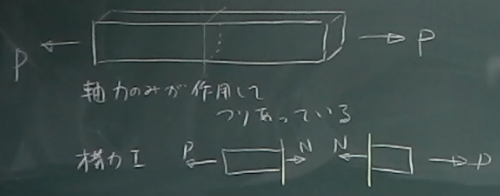 図のように空中にういた梁が両端を$P$で引っ張られてつりあっている
状態を考える。
この梁の適当なところを切断して内力が見えるようにしてやると、
構造力学Iの捉え方では、
2つの切断面に軸力$N$が作用・反作用の関係で作用して、
切り離されたそれぞれのピースでは力がつりあっていることになっていた。
図のように空中にういた梁が両端を$P$で引っ張られてつりあっている
状態を考える。
この梁の適当なところを切断して内力が見えるようにしてやると、
構造力学Iの捉え方では、
2つの切断面に軸力$N$が作用・反作用の関係で作用して、
切り離されたそれぞれのピースでは力がつりあっていることになっていた。
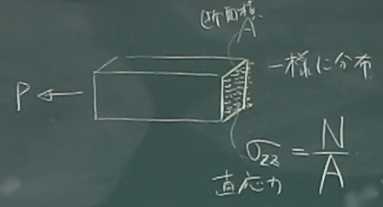 でも、これは断面に作用する「応力」の分布を、
ひとつの軸力$N$にまとめたのであって、
実際には、図のように断面の各部分に内力(応力)が分布している。
これを合計してまとめたものが軸力$N$だ。
今、梁が十分に細長いとすると
(端部の外力は図心の点を$P$で引っ張っているのだとしても)、
端部から十分に離れた断面の内力は、軸方向に一様に分布していると考えてもいいだろう。
あるいは、断面に一様な軸方向の力が発生するように、
端部表面の各部分を合計が$P$になるような力で理想的に引っ張ったことにしてもいい。
このように、断面に軸方向の一様な内力が発生している場合、
その内力の合計つまり軸力$N$を断面の断面積$A$で割って、
圧力の次元にした以下の物理量を「直応力」または「垂直応力」と言う。
でも、これは断面に作用する「応力」の分布を、
ひとつの軸力$N$にまとめたのであって、
実際には、図のように断面の各部分に内力(応力)が分布している。
これを合計してまとめたものが軸力$N$だ。
今、梁が十分に細長いとすると
(端部の外力は図心の点を$P$で引っ張っているのだとしても)、
端部から十分に離れた断面の内力は、軸方向に一様に分布していると考えてもいいだろう。
あるいは、断面に一様な軸方向の力が発生するように、
端部表面の各部分を合計が$P$になるような力で理想的に引っ張ったことにしてもいい。
このように、断面に軸方向の一様な内力が発生している場合、
その内力の合計つまり軸力$N$を断面の断面積$A$で割って、
圧力の次元にした以下の物理量を「直応力」または「垂直応力」と言う。
$\sigma_{zz}=\frac{N}{A}$
軸力$N$は引張が正で定義されているので、
直応力も引張が正、圧縮が負となる。
添字の$zz$は、
$z$面($z$軸に垂直な面)に作用する$z$方向の応力という意味であり、
直ひずみ$\varepsilon_{zz}$の発生と大きく関係する応力である。
3次元の一般的な物体を考えるなら
同様に、
$x$面に作用する$x$方向の$\sigma_{xx}$や
$y$面に作用する$y$方向の$\sigma_{yy}$も定義でき、
それぞれ
直ひずみ$\varepsilon_{xx}, \varepsilon_{yy}$の発生と関係する。
応力の次元は$\frac{力}{面積}$で圧力と同じであるので、
単位としては、N/m$^{2}$やPaを使う。
SI接頭語をつける場合は、MN/m$^{2}$とかMPaみたいに頭に1個だけ
接頭語をつけるのがSIの推奨だが、
構造分野やコンクリ分野などでは、習慣的にN/mm$^{2}$みたいな
(分母に接頭語のm(ミリ)が入る)
SI的には推奨されない表記も多用されている
(土質分野とかは割とSI準拠ではないかと思う)。
ちなみに、
N/mm$^{2}=$N/(10$^{-3}$m)$^{2}=$N/(10$^{-6}$m$^{2})
=10^{6}$N/m$^{2}=$MPaとなるので、N/mm$^{2}=$MPaというのさえ
覚えておけば、どちらで表記された応力を見ても、すぐに換算できる。
補足:
「応力」は英語ではstressで、材料分野など、物理一般の分野では、
この圧力の次元の応力のことを応力とかstressと言うのが一般的である。
ところが、日本の土木(昔)や建築(今も?)の分野では、
上記の内力$N$のことを「応力」と言い、$\sigma_{zz}$のことを「応力度」と言う
習慣が過去にあり、分野によっては、今も残っているかもしれない。
「応力」またはstressは、物理の広い分野で、
圧力の次元を持つ$\sigma$の意味で使われているので、
「応力」は常にこの意味で用いて、
「応力度」という言葉は(「許容応力度設計法」といった)用語になっているもの以外では
使わないのがいいだろう。
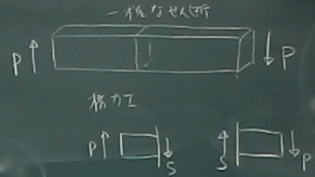 次に、図のように空中に浮いた梁が、
両端で一方は上向きに、他方は下向きに鉛直の力$P$を受けて、
鉛直方向の力はつりあっているものとする。
もちろん、これではモーメントはつりあわないから時計回りに回転してしまうので、
このモーメントとつりあう反対回りのモーメント外力をどこかに作用させないと
いけないが、とりあえず今は上下方向のつりあいだけ考えておく
(左端が固定された片持ち梁の右端を下向きに$P$だけ押したら、
左端に上向きに$P$の反力と反時計回りのモーメント反力が生じたということにしてもいい)。
次に、図のように空中に浮いた梁が、
両端で一方は上向きに、他方は下向きに鉛直の力$P$を受けて、
鉛直方向の力はつりあっているものとする。
もちろん、これではモーメントはつりあわないから時計回りに回転してしまうので、
このモーメントとつりあう反対回りのモーメント外力をどこかに作用させないと
いけないが、とりあえず今は上下方向のつりあいだけ考えておく
(左端が固定された片持ち梁の右端を下向きに$P$だけ押したら、
左端に上向きに$P$の反力と反時計回りのモーメント反力が生じたということにしてもいい)。
 このとき、(上の直応力のときと同じような論法で)
梁の端部から十分に離れた断面では、図のように断面に平行な内力が
一様に分布しているものとする。
このとき、
この断面に平行な内力の合計つまりせん断力$S$を断面の断面積$A$で割って、
圧力の次元にした以下の物理量を「せん断応力」と言う。
このとき、(上の直応力のときと同じような論法で)
梁の端部から十分に離れた断面では、図のように断面に平行な内力が
一様に分布しているものとする。
このとき、
この断面に平行な内力の合計つまりせん断力$S$を断面の断面積$A$で割って、
圧力の次元にした以下の物理量を「せん断応力」と言う。
$\sigma_{zy}=\frac{S}{A}$
添字の$zy$は、
$z$面($z$軸に垂直な面)の$y$方向の応力という意味で、
$y$面の$z$方向の応力であれば、$\sigma_{yz}$となるが、
実は、$\sigma_{yz}=\sigma_{zy}$という関係があるので、
一般には、$\sigma_{yz}$の表記を用いる。
なぜそうなるかという話に興味がある人は
この辺。
だから、$yz$平面で考えている梁のせん断応力ということであれば、
以下のように書いて構わない。
$\sigma_{yz}=\frac{S}{A}$
せん断応力の正の向きは、梁の場合、せん断力の正の向きと同様に、
「右下がりが正」と考えておいてよい。
3次元の一般的な物体については、やや難しい話になるが、興味のある人は
この辺。
まあ、これは2次元の話だが。
3次元の一般的な物体を考えるなら、
$x$面に作用する$y$方向の応力
$\sigma_{xy}$や
$z$面に作用する$x$方向の応力
$\sigma_{zx}$も同様に定義できる。
そして、せん断応力
$\sigma_{xy}, \sigma_{yz}, \sigma_{zx}$は、
せん断ひずみ
$\varepsilon_{xy}, \varepsilon_{yz}, \varepsilon_{zx}$と
それぞれ比例関係にある。これについては下で述べる。
 整理すると、直応力には $\sigma_{xx}, \sigma_{yy}, \sigma_{zz}$の3成分、
せん断応力には、
$\sigma_{xy}, \sigma_{yz}, \sigma_{zx}$の3成分があることになるが、
外力を受けて応力が発生し、つりあっている物体の
内部の微小部分を取り出したときに、
これらの応力がどのような状態でつりあっているかという
イメージをおおまかに説明しておく。
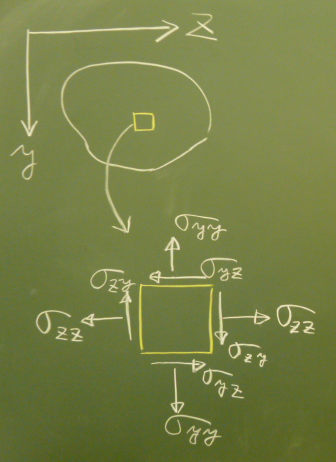
3次元の場合は、微小な立方体を取り出すべだが、
簡単のため、図のように$yz$平面で考え、微小な正方形を取り出し、
その切断面に作用する応力を考える。
既に述べたように、応力の添字の意味は、$\sigma_{yz}$だったら、
$y$面($y$軸に直角な面)に作用する$z$方向の応力ということだ。
応力のつりあいから$\sigma_{yz}=\sigma_{zy}$となるが、
この図では、添字の意味を理解するため、$\sigma_{yz}$と$\sigma_{zy}$を
区別して書いている。
その際、$y$面と言っても、
外向き法線が$y$の正方向を向いている面(この図では下の面)と
外向き法線が$y$の負方向を向いている面(この図では上の面)がある。
前者を$+y$面、後者を$-y$面とすると、
$+y$面に作用する応力は座標の正の向きに、
$-y$面に作用する応力は座標の負の向きに、
作用させる。
そうすると、直応力は互いに向かい合う面どおしで、
互いに外向きとなり、
つまり、直応力は引張が正となっている。
また、せん断応力の場合は、
向かい合う2面で、互いに逆向きになっていて
この正方形の右下と左上をつまんで引っ張った方向に
せん断変形する向きが正である。
これは、$z$軸に横たわる梁の微小部分が、
右下がりにせん断変形した際の変形と対応している。
このように直応力が直ひずみの発生と関係し、
せん断応力がせん断ひずみの発生と関係することをイメージできるように
なってほしい。
ちなみに、$xy$座標で考える場合は、
例えば、$\sigma_{xy}$は
上の規則に従って、$+x$面の$+x$の向きと$-x$面の$-x$の向きに作用することになる。
また、ここではこの微小正方形の向かい合う2面
($+y$面と$-y$面、$+z$面と$-z$面)に作用する
2組の直応力どうし
(
$+y$方向の$\sigma_{yy}$と
$-y$方向の$\sigma_{yy}$、
$+z$方向の$\sigma_{zz}$と
$+z$方向の$\sigma_{zz}$)がつりあっていて、
2組のせん断応力どうし
(
$+z$方向の$\sigma_{yz}$と
$-z$方向の$\sigma_{yz}$、
$+y$方向の$\sigma_{zy}$と
$-y$方向の$\sigma_{zy}$)がつりあっているというつりあいを
考えているが、応力はこの微小部分の中でも変化し得るため、
もっと厳密な応力のつりあいに興味がある人は、
この辺参照。
$\sigma_{yz}=\sigma_{zy}$になる理由も書いてある。
整理すると、直応力には $\sigma_{xx}, \sigma_{yy}, \sigma_{zz}$の3成分、
せん断応力には、
$\sigma_{xy}, \sigma_{yz}, \sigma_{zx}$の3成分があることになるが、
外力を受けて応力が発生し、つりあっている物体の
内部の微小部分を取り出したときに、
これらの応力がどのような状態でつりあっているかという
イメージをおおまかに説明しておく。
3次元の場合は、微小な立方体を取り出すべだが、
簡単のため、図のように$yz$平面で考え、微小な正方形を取り出し、
その切断面に作用する応力を考える。
既に述べたように、応力の添字の意味は、$\sigma_{yz}$だったら、
$y$面($y$軸に直角な面)に作用する$z$方向の応力ということだ。
応力のつりあいから$\sigma_{yz}=\sigma_{zy}$となるが、
この図では、添字の意味を理解するため、$\sigma_{yz}$と$\sigma_{zy}$を
区別して書いている。
その際、$y$面と言っても、
外向き法線が$y$の正方向を向いている面(この図では下の面)と
外向き法線が$y$の負方向を向いている面(この図では上の面)がある。
前者を$+y$面、後者を$-y$面とすると、
$+y$面に作用する応力は座標の正の向きに、
$-y$面に作用する応力は座標の負の向きに、
作用させる。
そうすると、直応力は互いに向かい合う面どおしで、
互いに外向きとなり、
つまり、直応力は引張が正となっている。
また、せん断応力の場合は、
向かい合う2面で、互いに逆向きになっていて
この正方形の右下と左上をつまんで引っ張った方向に
せん断変形する向きが正である。
これは、$z$軸に横たわる梁の微小部分が、
右下がりにせん断変形した際の変形と対応している。
このように直応力が直ひずみの発生と関係し、
せん断応力がせん断ひずみの発生と関係することをイメージできるように
なってほしい。
ちなみに、$xy$座標で考える場合は、
例えば、$\sigma_{xy}$は
上の規則に従って、$+x$面の$+x$の向きと$-x$面の$-x$の向きに作用することになる。
また、ここではこの微小正方形の向かい合う2面
($+y$面と$-y$面、$+z$面と$-z$面)に作用する
2組の直応力どうし
(
$+y$方向の$\sigma_{yy}$と
$-y$方向の$\sigma_{yy}$、
$+z$方向の$\sigma_{zz}$と
$+z$方向の$\sigma_{zz}$)がつりあっていて、
2組のせん断応力どうし
(
$+z$方向の$\sigma_{yz}$と
$-z$方向の$\sigma_{yz}$、
$+y$方向の$\sigma_{zy}$と
$-y$方向の$\sigma_{zy}$)がつりあっているというつりあいを
考えているが、応力はこの微小部分の中でも変化し得るため、
もっと厳密な応力のつりあいに興味がある人は、
この辺参照。
$\sigma_{yz}=\sigma_{zy}$になる理由も書いてある。
上で述べたように、
3次元の一般的な物体の内部に作用する応力は、
3つの直応力
$\sigma_{xx}, \sigma_{yy}, \sigma_{zz}$ と
3つのせん断応力
$\sigma_{xy}, \sigma_{yz}, \sigma_{zx}$ の
計6つの成分がある。
そうすると、
こうした応力の成分は、前回やった3つの直ひずみ
$\varepsilon_{xx}, \varepsilon_{yy}, \varepsilon_{zz}$ や
3つのせん断ひずみ
$\varepsilon_{xy}, \varepsilon_{yz}, \varepsilon_{zx}$ と
関係づけられそうな感じがするが、
実はこれはこれでなかなか難しい話になる。
3次元の応力—ひずみ関係の
一般的な話に興味がある人は、
この辺参照。
ここでは、等方性材料(どの向きでも力学的性質が変わらない)の
応力とひずみの関係について、導出は抜きにして、
結果だけ教える。
まず、直ひずみと直応力との間には、
以下のような関係がある。
$
\left(
\begin{array}{c}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\varepsilon_{zz}
\end{array}
\right)
=
\frac{1}{E}
\left(
\begin{array}{rrr}
1 & -\nu & -\nu \\
-\nu & 1 & -\nu \\
-\nu & -\nu & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
\sigma_{xx}\\
\sigma_{yy}\\
\sigma_{zz}
\end{array}
\right)
$
これの逆行列をとって逆関係を導くと、以下のようにも書ける。
$
\left(
\begin{array}{c}
\sigma_{xx}\\
\sigma_{yy}\\
\sigma_{zz}
\end{array}
\right)
=
\frac{E}{(1+\nu)(1-2\nu)}
\left(
\begin{array}{ccc}
1-\nu & \nu & \nu \\
\nu & 1-\nu & \nu \\
\nu & \nu & 1-\nu \\
\end{array}
\right)
\left(
\begin{array}{c}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\varepsilon_{zz}
\end{array}
\right)
$
ここに$E$はヤング率で、次元は応力と同じ$\frac{力}{面積}$だ。
ヤング率は、材料の固さを表し、これが大きくなるほど材料は固くなる。
例えば、木材(杉)のヤング率は6GPaぐらい、
鋼材のヤング率は200GPaぐらい。
$\nu$はポアソン比で、後でまた説明するが、
細長い棒を縦に引っ張ったときの縦方向(のび)と横方向(縮み)の直ひずみの比である。
こういう応力とひずみの関係式のことを構成則と言うこともある。
ここでは、わかりやすく
応力—ひずみ関係と言っておくが、
上の式は、特に覚えなくても構わない。
ただ、ある座標方向の直応力(たとえば$z$軸方向の$\sigma_{zz}$)は、
その座標方向の直ひずみ($z$軸であれば$\varepsilon_{zz}$)とだけ
関係するのではなく、他の方向の直ひずみとも関係しているということは、
理解しておいてほしい。
この応力とひずみの関係は、次項の「1次元のフックの法則」に対して
3次元のフックの法則と言ってもいいかもしれない。
ちなみに、「一般化されたフックの法則」の話はちょっと難しいが、
興味のある人はこの辺。
なお、2次元のフックの法則というか応力―ひずみ関係というのは、
3次元から2次元への落とし方によって、
平面応力状態と
平面ひずみ状態とがあり、
注意が必要である。
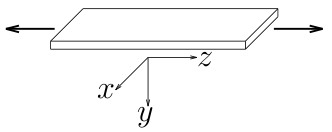 例えば、薄い板を細長く切り出して、
細長い方向に引っ張るような問題を考える場合、
板厚方向を$y$, 細長い方向を$z$とすると、
$\sigma_{zz}$以外の応力成分は無視できるような状態になるので、
上の直ひずみと直応力の関係式
に$\sigma_{xx}=\sigma_{yy}=0$を代入すると、
例えば、薄い板を細長く切り出して、
細長い方向に引っ張るような問題を考える場合、
板厚方向を$y$, 細長い方向を$z$とすると、
$\sigma_{zz}$以外の応力成分は無視できるような状態になるので、
上の直ひずみと直応力の関係式
に$\sigma_{xx}=\sigma_{yy}=0$を代入すると、
$
\left(
\begin{array}{c}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\varepsilon_{zz}
\end{array}
\right)
=
\frac{1}{E}
\left(
\begin{array}{rrr}
1 & -\nu & -\nu \\
-\nu & 1 & -\nu \\
-\nu & -\nu & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
0\\
0\\
\sigma_{zz}
\end{array}
\right)
$
から、
$\varepsilon_{x x}=-\frac{\nu\sigma_{zz}}{E}$
$\varepsilon_{yy}=-\frac{\nu\sigma_{zz}}{E}$
$\varepsilon_{zz}=\frac{\sigma_{zz}}{E}$
となるから、これらを整理して、
$\sigma_{zz}=E\varepsilon_{zz}$
$\nu=-\frac{\varepsilon_{x x}}{\varepsilon_{zz}}=
-\frac{\varepsilon_{yy}}{\varepsilon_{zz}}$
という関係が得られる。
$\sigma_{zz}=E\varepsilon_{zz}$は1次元のフックの法則である。
土木の学部の範囲の話では、
直応力と直ひずみの関係は、ほぼ、この1次元のフックの法則だけで
話が済んでしまうが、
それはあくまで、
例えば、梁のような細長い棒を扱っているとか、
コンクリートや土質の円柱状の試験体みたいなものを一様に均等に圧縮しているとか、
1次元のフックの法則がなりたつような条件で議論しているから
ということを忘れてはいけない。
$\nu=-\frac{\varepsilon_{xx}}{\varepsilon_{zz}}$
または
$\nu=-\frac{\varepsilon_{yy}}{\varepsilon_{zz}}$
はポアソン比である。
$z$方向に長い試験体を$z$方向に引っ張った場合、
$z$方向を縦方向、その直角方向を横方向と言い、
縦方向の直ひずみを縦ひずみ、横方向の直ひずみを横ひずみと言うが、
縦ひずみに対する横ひずみの比がポアソン比となる。
マイナスがついているが、
直ひずみは引張が正なので、細長い棒を引っ張った場合は、
縦ひずみは引っ張られる方向なので正になり、
横ひずみは縮む方向なので負になり、
ポアソン比の値としては正になる。
コンクリート供試体みたいなものを圧縮したときは、これの逆で、
圧縮してる側の縦ひずみは負になり、
横ひずみは膨れて正になるので、やはりポアソン比の値としては正になる。
ちなみに3年次の土木環境工学実験の構造実験では、
この
$\sigma_{zz}=E\varepsilon_{zz}$を使ってヤング率を測定し、
$\nu=-\frac{\varepsilon_{yy}}{\varepsilon_{zz}}$を使って
ポアソン比を求める。
ポアソン比の定義から考えると、
例えば、円柱状の材料に一様な圧縮をかけているのに、
横方向に全く膨れない(横ひずみがない)とすれば、
ポアソン比は0となる。
例えば、コルクとかスポンジみたいな材料だと、
縦に押されても横方向にほとんど膨れないので、ポアソン比は0に近くなる。
つまり、ポアソン比の最小値は0ということだ。
では、ポアソン比の最大値はどうなるだろうか。
一般的な材料では、縦に圧縮されると、縦方向に縮むので、
縦に押されて減った体積のぶんだけ横に膨れるということにはならない。
しかし、例えば水みたいに圧縮されてもほとんど縮まない材料の場合は、
縦に押されて縦方向に縮むと、その縮んだ体積のぶんだけ横に膨れてしまう。
こういう状態がポアソン比の最大値だ。
ちなみにこの最大値は0.5だが、
なぜそうなるかに興味のある人は、この辺参照。
ちなみに、木材とか内部構造を持つ材料の場合は、
測定方法によってはポアソン比が0.5を超えたりすることもある。
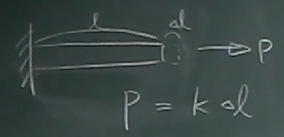 応力とひずみの関係で表される1次元のフックの法則
$\sigma_{zz}=E\varepsilon_{zz}$
と、中学や高校で習う力とのびの関係で表されるフックの法則の関係を確認しておく。
図のような長さ$\ell$の棒を外力$P$で引っ張って、
棒が$\Delta\ell$だけ伸びたら、
$P$と$\Delta\ell$には比例関係があり、比例定数(ばね定数)を$k$とすると
$P=k\Delta\ell$と書ける。
でも、高校の教科書とかをよく読んでみると、
ばねの弾性力と伸びが比例すると書いてあり、
構造力学の言葉で言い直せば、内力(つまり軸力$N$)と伸びが比例するということだ。
もちろん、この棒をどこかで切って軸力が見える状態にすれば、
どこで切っても$N=P$の軸力が生じている。
だから、高校の教科書のフックの法則の意味は、
応力とひずみの関係で表される1次元のフックの法則
$\sigma_{zz}=E\varepsilon_{zz}$
と、中学や高校で習う力とのびの関係で表されるフックの法則の関係を確認しておく。
図のような長さ$\ell$の棒を外力$P$で引っ張って、
棒が$\Delta\ell$だけ伸びたら、
$P$と$\Delta\ell$には比例関係があり、比例定数(ばね定数)を$k$とすると
$P=k\Delta\ell$と書ける。
でも、高校の教科書とかをよく読んでみると、
ばねの弾性力と伸びが比例すると書いてあり、
構造力学の言葉で言い直せば、内力(つまり軸力$N$)と伸びが比例するということだ。
もちろん、この棒をどこかで切って軸力が見える状態にすれば、
どこで切っても$N=P$の軸力が生じている。
だから、高校の教科書のフックの法則の意味は、
$N=k\Delta\ell$
ということである。
(この辺の話に興味のある人はこの辺参照)。
さて、この式の左辺を直応力$\sigma_{zz}=\frac{N}{A}$で表すために、
両辺を断面積$A$で割る。
$\frac{N}{A}=\frac{k}{A}\Delta\ell$
また、右辺の伸びを直ひずみで表したいが、
初期状態$\ell$から$\Delta\ell$だけ均等に(線形的に)伸びた場合の
直ひずみは、第2回の例題4でやったように、
$\varepsilon_{zz}=\frac{\Delta\ell}{\ell}$で表される。
なので、右辺の伸びがひずみになるように変形する。
$\frac{N}{A}=\frac{k\ell}{A}\frac{\Delta\ell}{\ell}$
ここで、$\sigma_{zz}=\frac{N}{A}$, $\varepsilon_{zz}=\frac{\Delta\ell}{\ell}$
に書き換え、それらの比例定数を$E=\frac{k\ell}{A}$とおくなら、
$\sigma_{zz}=E\varepsilon_{zz}$
になる。というわけで、応力とひずみで表した1次元のフックの法則も、
軸力と伸びで表した1次元のフックの法則も、次元が違うだけで同じことを表している。
また、$E=\frac{k\ell}{A}$の関係から、
棒のばね定数は次式で表される。
${\displaystyle k=\frac{EA}{\ell}\;\;\;\;}$
(重要)
これはとても大事な式なので、覚えておくこと。
分子にあるヤング率$E$が大きくなれば、ばねは固くなるし、
棒を太くして断面積$A$を大きくすれば、ばねは固くなるし、
棒を長くして
分母にある$\ell$を大きくすれば、
ばねは柔らかくなることは、直感とも対応するだろう。
ばね定数は、このように棒の断面積や長さによって変わってしまう量だから、
材料の固さを表す量としては、設計等に使う場合は便利ではない。
だって、この棒のばね定数は1.5MN/mだと教えられたところで、
形を変えたらばね定数は変わってしまうのだ。
そういう意味では、ヤング率は、ある材料に対して一定の値だから、
設計等の際は扱いやすい。また、
材料がどれくらいの力に耐えられるかといった話も、
力の次元で議論するよりも、応力の次元で議論した方が、
対象としている構造物の大きさに関わらず比較ができて議論がしやすいということもある。
さて、せん断応力$\sigma_{xy}, \sigma_{yz}, \sigma_{zx}$
とせん断ひずみ$\varepsilon_{xy}, \varepsilon_{yz}, \varepsilon_{zx}$の
間にはどのような関係があるのだろうか。
これも
導出は抜きにして、
結果だけ示すと、
$\sigma_{xy}=2G \varepsilon_{xy}$
$\sigma_{yz}=2G \varepsilon_{yz}$
$\sigma_{zx}=2G \varepsilon_{zx}$
と表される。$G$はせん断弾性係数で、これもヤング率と同じく次元は$\frac{力}{面積}$だ。
直応力と直ひずみの関係に比べると、
ただの比例関係なので拍子抜けするかもしれない。
等方性材料のヤング率$E$とポアソン比$\nu$, せん断弾性係数$G$の間には、
以下の関係があるので覚えておいてほしい。
${\displaystyle G=\frac{E}{2(1+\nu)}}\;\;\;\;$
(重要)
等方性材料の場合、ポアソン比は$0\le\nu\le 0.5$の範囲にあるから、
せん断弾性係数というのは、大きくてもヤング率の半分ぐらい、
小さくてもヤング率の$\frac{1}{3}$ぐらいの値になる。
木材のような異方性材料(繊維方向があったりして、向きによって力学的性質が異なる)の
場合は、この式は成り立たず、
例えば木材の場合は、せん断弾性係数は軸方向ヤング率の$\frac{1}{15}$ぐらい
になったりする。
ちなみに3年次の土木環境工学実験の構造実験では、
アクリル板の
ヤング率とポアソン比を測定し、この式を使ってせん断弾性係数を求める。
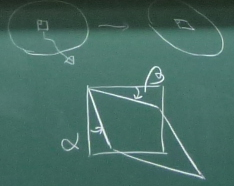 さて、第2回で
「せん断ひずみ」には、
角度変形$\alpha$, $\beta$の平均で表される
さて、第2回で
「せん断ひずみ」には、
角度変形$\alpha$, $\beta$の平均で表される
せん断ひずみ:
${\displaystyle
\varepsilon_{yz}=\frac{\alpha+\beta}{2}
}$
の他に、2で割らない
工学せん断ひずみ:
${\displaystyle
\gamma_{yz}=\alpha+\beta
}$
があるという話をしたが、工学せん断ひずみを用いて、せん断応力と
せん断ひずみの関係を書くと、
$\sigma_{xy}=G \gamma_{xy}$
$\sigma_{yz}=G \gamma_{yz}$
$\sigma_{zx}=G \gamma_{zx}$
となる。
工学せん断ひずみで表現していても、「せん断ひずみ」としか言わない場合も
あるので、式を見て$G$が2倍になっているかどうかで
どちらのせん断ひずみかを判断する必要がある。
土木の学部レベルでこの式が出てくる場合は、
たぶん、特定の平面のせん断応力と工学せん断ひずみを
それぞれ$\tau$と$\gamma$で表して、$\tau=G\gamma$のような式が使われる
ことが多いのではないかと思う(土質とかコンクリとかも?)。
構造力学(応用)で扱う初等梁モデルでは、
第2回の梁モデルの仮定でやったように、
平面保持の仮定と断面形不変の仮定からせん断ひずみはすべて0になるので、
この式が出てくることは、ほぼないと思う。
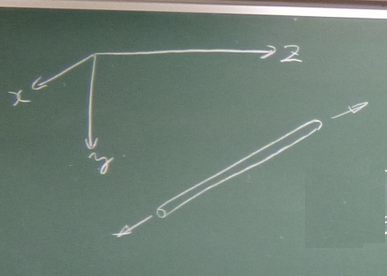 $x$軸に$\sigma_{yy}=\sigma_{zz}=0$と見なせる十分に
細長い棒が横たわっている。
この棒について、1次元のフックの法則を導け。
また、ポアソン比$\nu$をひずみを用いて表わせ。
ひずみと応力は以下の関係にある。
$x$軸に$\sigma_{yy}=\sigma_{zz}=0$と見なせる十分に
細長い棒が横たわっている。
この棒について、1次元のフックの法則を導け。
また、ポアソン比$\nu$をひずみを用いて表わせ。
ひずみと応力は以下の関係にある。
$
\left(
\begin{array}{c}
\varepsilon_{xx}\\
\varepsilon_{yy}\\
\varepsilon_{zz}
\end{array}
\right)
=
\frac{1}{E}
\left(
\begin{array}{rrr}
1 & -\nu & -\nu \\
-\nu & 1 & -\nu \\
-\nu & -\nu & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
\sigma_{xx}\\
\sigma_{yy}\\
\sigma_{zz}
\end{array}
\right)
$
答えはここ。
学生実験で、 アクリル材の引張試験を行ったところ、 ヤング率の測定値が3.2GPa, ポアソン比の測定値が0.30であった。 せん断弾性係数を求めよ。 答えは、ここ。
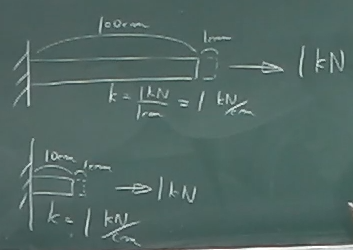 今、一端が壁に固定されている1mの棒と
10cmの棒それぞれの先端を1kNで引っ張ったところ、
どちらの棒も先端が1cmだけ伸びたとする。
このとき、1mの棒と10cmの棒それぞれのばね定数を求めよ。
今、一端が壁に固定されている1mの棒と
10cmの棒それぞれの先端を1kNで引っ張ったところ、
どちらの棒も先端が1cmだけ伸びたとする。
このとき、1mの棒と10cmの棒それぞれのばね定数を求めよ。
また、この棒の断面積がどちらも1cm$^{2}$だとするとき、
棒の断面に作用する直応力$\sigma_{zz}$を求めよ。
また、それぞれの棒の直ひずみ$\varepsilon_{zz}$を求め、
それぞれの棒のヤング率を求めよ。
1次元のフックの法則が成り立つものとしてよい。
どちらの棒がより固いか。
答えはここ。
2022年度小テスト:
小テスト221102(解答)
2021年度小テスト:
問,
解答
2020年度小テスト:
問1,
解答
メモ: