![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
| 日付 | 時間 | 作業時間 | 内容 | 立会 |
| 10/16 | 14:30-16:00 | 1.5 | 顔合わせ、ノートPCの立ち上げ | 後藤さん |
| 10/23 | 14:30-16:00 | 1.5 | UNIXコマンド練習 | 後藤さん |
| 10/30 | 14:00-16:00 | 1.5 | viの練習、gnuplotの使い方 | 後藤さん |
| 11/6 | 14:00-18:00 | 4.0 | Salome-mecaの使い方 | 後藤さん |
| 11/12 | 15:00-17:30 | 2.5 | 11/6課題 | |
| 11/19 | 16:30-19:30 | 3.0 | 11/13課題 | |
| 11/20 | 13:00-16:30 | 3.5 | Salome-meca 木材 直行異方性 | 後藤さん |
| 11/26 | 14:30-18:00 | 3.5 | 11/20課題 | |
| 12/4 | 13:30-17:00 | 3.5 | Salome-meca 2材料 zoom | 後藤さん |
| 12/10 | 16:30-19:00 | 2.5 | 12/4課題 | |
| 12/11 | 12:00-18:30 | 6.5 | TeX | 後藤さん |
| 12/18 | 10:00-16:30 | 6.5 | TeX 画像の貼り方(gnuplot) | 後藤さん |
| 1/22 | 13:30-16:30 | 3.0 | 最終課題 | 後藤さん |
| 1/28 | 16:00-18:00 | 2 | 最終課題 | |
| 1/29 | 16:30-19:00 | 2.5 | 最終課題 | 後藤さん |
| 2/4 | 15:00-16:30 | 3.5 | 最終課題 | 後藤さん |
| 2/5 | 12:00-17:00 | 5.0 | 最終課題提出 | 後藤さん |
| 2/10 | 17:00-18:30 | 1.5 | パワポ作成 | |
| 2/12 | 13:00-16:30 | 3.5 | 最終課題発表 | 後藤さん |
| 2/16 | 9:00-19:00 | 10 | 卒論見学 春休み課題 | |
| 2/17 | 9:00-16:00 | 7 | 卒論見学 春休み課題 | |
| 3/8 | 12:00-15:30 | 3.5 | 春休み課題 | |
| 3/9 | 12:30-15:00 | 2.5 | ゼミ | 後藤さん |
| 3/23 | 10:00-13:00 | 3.0 | 研究室掃除 | 後藤さん 及川さん 小川さん |
| 3/24 | 11:00-17:30 | 6.5 | 研究室模様替え | 後藤さん 及川さん 小川さん 青山さん |
| 3/25 | 11:00-17:30 | 6.5 | 春休み課題 | 後藤さん 及川さん |
| 4/12 | 13:00~14:30 | 1.5 | ゼミ | 後藤さん |
| 4/14 | 10:30~17:30 | 7.0 | 外国文献 冬休み課題 | 後藤さん 石黒さん 青木さん M1 M2 |
| 4/19 | 12:30~17:00 | 4.5 | ゼミ(春休み課題発表、卒論決め) | 後藤さん 石黒さん 青木さん M1 M2 |
| 4/23 | 15:30~18:00 | 2.5 | 対傾構モデル作成(アスタースタディの途中まで) | M1 M2 |
| 4/26 | 10:30~18:00 | 7.5 | ゼミ 対傾構モデルの見直し | 後藤さん 青木さん M1 M2 |
| 5/17 | 11:30~18:30 | 7.0 | ゼミ 対傾構モデルの見直し | 後藤さん 青木さん 石黒さん M1 M2 |
| 5/21 | 14:00~18:30 | 4.5 | オンサイト木橋のモデルを解析したい | 後藤さん 石黒さん 青木さん M1 |
| 5/24 | 14:00~17:30 | 3.5 | 方向性決定 | 後藤さん 青木さん M1 M2 |
| 5/28 | 16:00~19:30 | 3.5 | モデル作成中 | M1 M2 |
| 5/31 | 11:30~16:30 | 5.0 | モデル作成中 | 後藤さん 青木さん M1 M2 |
| 6/1 | 10:30~14:00 | 3.5 | 海老さんのモデルをフューズしたものの解析 | 後藤さん 青木さん M1 |
| 6/7 | 11:00~17:30 | 6.5 | 経過報告と見直し | 後藤さん 青木さん M1 M2 |
| 6/14 | 13:00~16:30 | 3.5 | ゼミ | 後藤さん 青木さん M1 M2 |
| 7/26 | 12:00~17:00 | 5.0 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 8/28 | 15:00~18:00 | 3.0 | ||
| 8/30 | 15:00~19:30 | 4.5 | ||
| 8/31 | 13:00~17:00 | 4.0 | 経過報告 | 後藤さん 青木さん 石黒さん 近藤さん M1 M2 |
| 9/23 | 14:00~22:30 | 8.5 | オンサイト木橋(CLT)モデル作成 tex | M1 M2 |
| 9/28 | 7:00~16:00 | 9.0 | 中間発表 | 後藤さん 青木さん 石黒さん M1 M2 |
| 10/4 | 10:00~16:00 | 6.0 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 10/10 | 15:30~20:00 | 4.5 | ||
| 10/16 | 15:00~17:30 | 2.5 | ||
| 10/16 | 19:00~21:30 | 2.5 | ||
| 10/31 | 17:00~23:00 | 6.0 | ||
| 11/1 | 10:00~18:00 | 8.0 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 11/8 | 14:00~17:00 | 3.0 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 11/15 | 14:00~17:00 | 3.0 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 11/19 | 12:00~18:00 | 6.0 | 3年ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 11/22 | 14:00~17:00 | 3.0 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 12/6 | 10:00~17:00 | 7.0 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 12/13 | 12:00~16:30 | 4.5 | ゼミ | 後藤さん 青木さん 石黒さん M1 M2 |
| 平均たわみ | |
| 海老さんのモデル | 9.17mm |
| CLTモデル | 9.54mm |
| 強軸の方向 | 平均たわみ | |
| 幅員方向 | 16.64mm | |
| 橋軸方向 | 9.54mm |
| 強軸の方向 | 平均たわみ | 手計算 | 誤差 | 手計算(穴有り) | 誤差(穴有り) | |
| 幅員方向 | 16.56mm | 14.31mm | 15.72% | 14.58mm | 13.58% | |
| 橋軸方向 | 9.40mm | 7.81mm | 20.36% | 7.89mm | 19.14% |
| 弱軸方向ヤング率 | 0.585GPa |
| 強軸方向ヤング率 | 5.265GPa |
| 板厚方向ヤング率 | 0.211GPa |
| 強軸直行面のせん断弾性係数 | 0.039GPa |
| 弱軸直行面のせん断弾性係数 | 0.351GPa |
| CLTの板面のせん断弾性係数 | 0.195Pa |
CLTの弱軸方向\( x \), 強軸方向\( y \), 板厚方向\( z \)とし、 \( E_{x}=0.585 \)GPa, \( E_{y}=5.265 \)GPa, \( E_{z}=0.211 \)GPaとする。
ポアソン比を\( \nu_{xy}, \nu_{yz}, \nu_{xz} \)の3つだけで書いたひずみー応力マトリクス
\( E_{x}=0.585 \)GPa, \( E_{y}=5.265 \)GPa, \( E_{z}=0.211 \)GPa, \( \nu_{xy}=\nu_{yz}=\nu_{xz}=0.016 \)を代入
ポアソン比が6つの表現
上記の値を代入して、
成分同士をイコールで結んで、
\( -\frac{0.016}{0.585}=-\frac{\nu_{yx}}{5.265} \)より、\( \nu_{yx}=0.144 \)
\( -\frac{0.016}{0.585}=-\frac{\nu_{zx}}{0.211} \)より、\( \nu_{zx}=0.0058 \)
\( -\frac{0.016}{5.265}=-\frac{\nu_{zy}}{0.211} \)より、\( \nu_{zy}=0.0006 \)
いずれも0.5を下回っているので、Salome-mecaに入力するポアソン比 \( \nu_{LT}=\nu_{xy}, \nu_{LN}=\nu_{xz}, \nu_{TN}=\nu_{yx} \) は、全て0.016にする。
| E_L | 3.5GPa | G_LN | 0.23GPa | NU_LN | 0.016 | ||
| E_N | 1.7GPa | G_NT | 0.23GPa | NU_LT | 0.016 | ||
| E_T | 1.7GPa | G_TN | 0.23GPa | NU_TN | 0.016 |
| E | 206GPa |
| NU | 0.3 |
| 平均たわみ | 13.39mm |
| 理論値(穴無し) | 11.94mm |
| 誤差 | 12.14% |
| 理論値(穴有り) | 12.121mm |
| 誤差 | 10.46% |
| E_L | 0.308GPa | G_LN | 0.513GPa | NU_LN | 0.016 | ||
| E_N | 7.694GPa | G_LT | 0.513GPa | NU_LT | 0.016 | ||
| E_T | 0.308GPa | G_TN | 0.513GPa | NU_TN | 0.016 |
| E | 206GPa |
| NU | 0.3 |
| 平均たわみ | 8.63mm |
| 理論値(穴無し) | 7.41mm |
| 誤差 | 16.51% |
| 理論値(穴有り) | 7.484mm |
| 誤差 | 15.21% |
| B×H | 840×534mm |
| 長さ | 7m |
| E_CLT | 3.5GPa(強軸)1.7GPa(弱軸) |
| ポアソン比(CLT) | 0.016 |
| E_鋼 | 206GPa |
| ポアソン比(鋼材) | 0.6 |
| 荷重 | 100kN |
| 平均たわみ | 13.39mm |
| 理論値(穴なし) | 11.94mm |
| ヤング率 | 支間長 | B×H | |
| CLT | 3.2GPa(強軸)1.7GPa(弱軸) | 7m | 840×120mm |
| H型鋼 | 206GPa | 7m | 200×300(294)mm |
| 平均たわみ | 誤差 | |
| 全体解析(100kN) | 12.25mm | 2.60% |
| 1/2解析(50kN) | 12.44mm | 4.19% |
| 1/4解析(25kN) | 12.51mm | 4.79% |
| 理論値 | 11.94mm | - |
| Salome-meca | 9.10mm |
| 手計算 | 8.4mm |
| 誤差 | 8.33% |
| Salome-meca | 9.18mm |
| 手計算 | 8.4mm |
| 誤差 | 9.29% |
| 支間長 | 7000mm |
| 厚さ | 600mm |
| 幅 | 840mm |
| I型鋼 | 300×150mm |
| 支間長 | 7m |
| 厚さ | 600mm |
| 幅 | 840mm |
| ヤング率 | 7.684GPa |
| 荷重 | 100kN |
0.429×0.5×3.65m 荷重-250kN

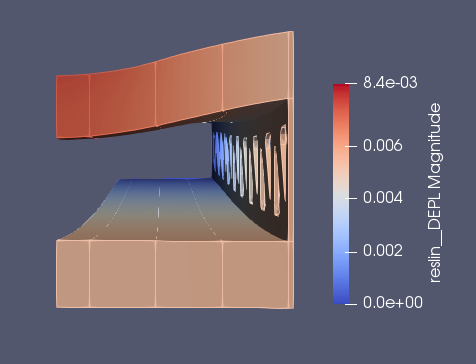
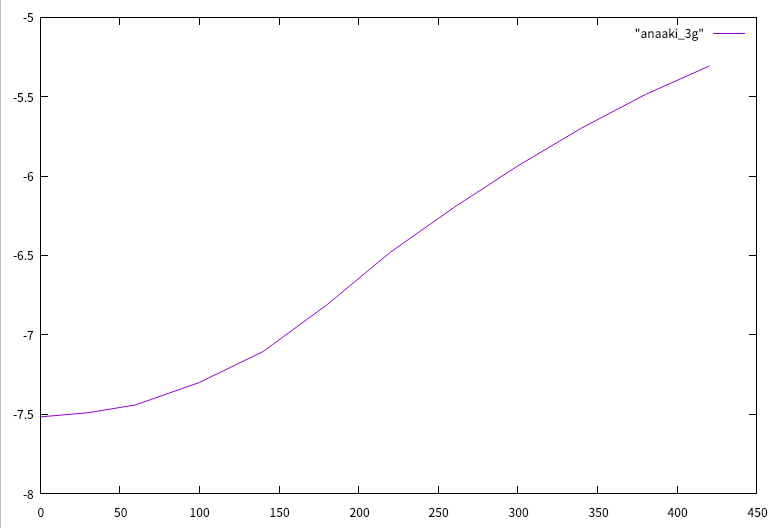 横軸-幅員方向 縦軸-たわみ(載荷方向が負)
横軸-幅員方向 縦軸-たわみ(載荷方向が負)
| ヤング率 | ポアソン比 | |
| 木材 | 7.694Gpa | 0.4 |
| 鋼材 | 206Gpa | 0.3 |
理論値 0.7552mm
理論値との相対誤差 2.9%
 載荷点の平均ひずみ 0.7772
基本のモデルとの誤差 0.0064%
理論値との相対誤差 2.9%
載荷点の平均ひずみ 0.7772
基本のモデルとの誤差 0.0064%
理論値との相対誤差 2.9%
 載荷点の平均ひずみ 0.7743
基本のモデルとの差 0.37%
理論値との相対誤差 0.25%
載荷点の平均ひずみ 0.7743
基本のモデルとの差 0.37%
理論値との相対誤差 0.25%
中立軸上に載荷線と固定端を乗せたことで、基本のモデルと1/4モデルの平均ひずみが以前よりかなり近い値になった。 誤差が限りなく小さいと判断し、次回からオンサイト木橋のモデルを解析していくこととする。
 載荷点の平均ひずみ 0.8446mm
基本ののモデルとの差 0.027%
載荷点の平均ひずみ 0.8446mm
基本ののモデルとの差 0.027%
 載荷点の平均ひずみ 0.5069mm
基本のモデルとの差 66.653%
載荷点の平均ひずみ 0.5069mm
基本のモデルとの差 66.653%
1/2モデルと基本のモデルのひずみは近い値になったが1/4モデルの方は割と大きな差が出た。境界条件や載荷の方法を見直し、近い値を出せるようにしたい。
理論値0.113556
| メッシュ長さ | 要素数 | 変位 | 相対誤差(%) |
| 0.8 | 222225 | 0.1154844 | 1.7 |
| 0.9 | 139827 | 0.112399 | -1.0 |
| 1.0 | 116578 | 0.114014 | 0.4 |
| 1.2 | 114433 | 0.113092 | -0.4 |
| 1.4 | 103032 | 0.112646 | -0.8 |
| 1.5 | 95670 | 0.111257 | -2.0 |
| 1.8 | 37841 | 0.105512 | -7.1 |
| 2.0 | 30815 | 0.102516 | -9.7 |
| 3.0 | 32150 | 0.099580 | -12.3 |
| 4.0 | 11503 | 0.083153 | -26.8 |
| 5.0 | 9556 | 0.070837 | -37.6 |
| 8.0 | 4540 | 0.039431 | -65.3 |
| 10.0 | 2282 | 0.008954 | -92.1 |
| メッシュ長さ | 要素数 | 変位 | 相対誤差(%) | 計算者 |
| 0.8 | 226647 | 0.08053 | 56.9 | 髙橋 |
| 0.9 | 127506 | 0.07678 | 49.7 | 髙橋 |
| 1.0 | 92447 | 0.05276 | 2.79 | |
| 1.2 | 88386 | 0.05264 | 2.55 | 田村 |
| 1.4 | 78086 | 0.05261 | 2.49 | 田村 |
| 1.5 | 70032 | 0.07255 | 41.3 | 根本 |
| 1.8 | 34858 | 0.068375 | 33.2 | 根本 |
| 2.0 | 20313 | 0.06328 | 23.3 | 藤原 |
| 3.0 | 18229 | 0.04892 | -4.68 | 君島 |
| 4.0 | 8067 | 0.050046 | -2.51 | 藤原 |
| 5.0 | 4846 | 0.036772 | -28.3 | 君島 |
| 8.0 | 3814 | 0.027088 | -47.2 | 森島 |
| 10.0 | 1716 | 0.02179 | -57.5 | 森島 |
長さ100mmの場合
| メッシュ長さ | 要素数 | 変位 | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.440015 | 11.9 | 君島 |
| 0.7 | 215780 | 0.435823 | 10.8 | 君島 |
| 0.8 | 159468 | 0.4330131 | 10.1 | 髙橋 |
| 0.9 | 71718 | 0.42766 | 8.72 | 髙橋 |
| 1.0 | 61315 | 0.423881 | 7.77 | |
| 1.2 | 58111 | 0.423005 | 7.54 | 田村 |
| 1.4 | 47409 | 0.420309 | 6.86 | 田村 |
| 1.5 | 42068 | 0.418470375 | 6.39 | 根本 |
| 1.8 | 24627 | 0.4104641 | 4.36 | 根本 |
| 2.0 | 12228 | 0.396314 | 0.84 | 藤原 |
| 4.0 | 5077 | 0.378695 | -3.6 | 藤原 |
| 8.0 | 1795 | 0.342299 | -12.7 | 森島 |
| 10.0 | 752 | 0.298709 | -24 | 森島 |
初等梁の理論値0.33333 ティモンシェン梁の理論値0.39333
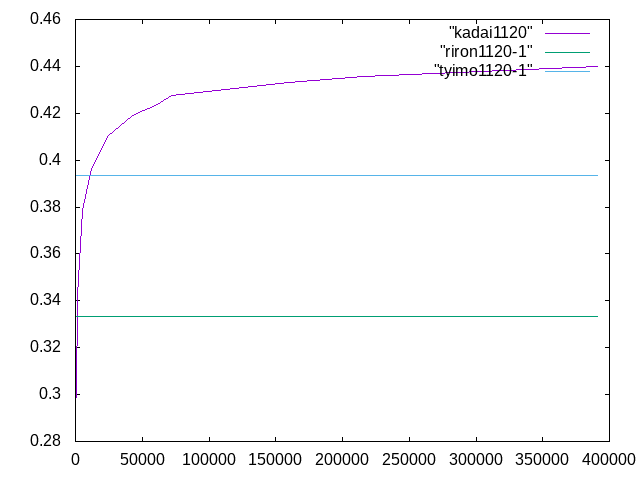
長さ50mmの場合
| メッシュの長さ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.5 | 215781 | 0.1253048 | 74.8 | 君島 |
| 0.7 | 109175 | 0.1172535 | 63.6 | 君島 |
| 0.8 | 75902 | 0.11527 | 60.8 | 高橋 |
| 0.9 | 71911 | 0.11416 | 59.3 | 高橋 |
| 1 | 47757 | 0.113602 | 58.5 | |
| 1.2 | 26945 | 0.108935 | 51.99 | 田村 |
| 1.4 | 22998 | 0.107298 | 49.71 | 田村 |
| 1.5 | 17689 | 0.10375025 | 44.77 | 根本 |
| 1.8 | 14668 | 0.1021334 | 42.51 | 根本 |
| 2 | 13986 | 0.069684 | -2.8 | 藤原 |
| 4 | 3009 | 0.048789575 | -32.0 | 藤原 |
| 8 | 967 | 0.0764429 | 7.2 | 森島 |
| 10 | 558 | 0.0768385 | 6.7 | 森島 |
初等梁の理論値0.041666 ティモンシェン梁の理論値0.071666
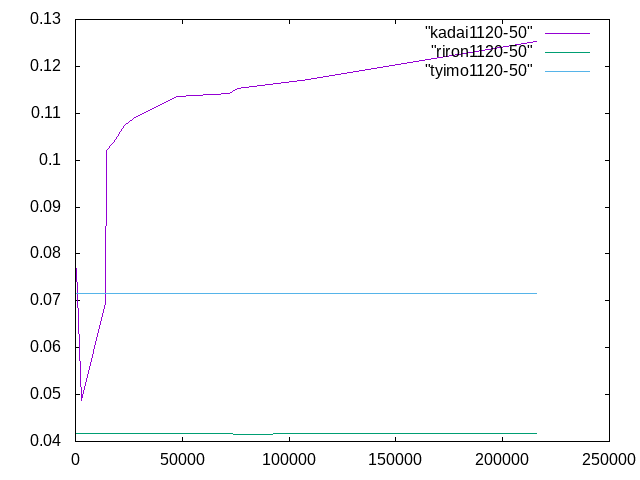
| メッシュ長さ | 要素数 | 変位 | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.341181238095 | 2.35 | 君島 |
| 0.7 | 215780 | 0.33798 | 1.39 | 君島 |
| 0.8 | 159468 | 0.33563 | 0.69 | 髙橋 |
| 0.9 | 71718 | 0.33203 | -0.39 | 髙橋 |
| 1.0 | 61315 | 0.32997 | -1.2 | |
| 1.2 | 58111 | 0.329956 | -1.2 | 田村 |
| 1.4 | 47409 | 0.328156 | -1.5 | 田村 |
| 1.5 | 42068 | 0.325074 | -2.4 | 根本 |
| 1.8 | 24627 | 0.317161 | -4.8 | 根本 |
| 2.0 | 12228 | 0.3005115 | -6.9 | 藤原 |
| 4.0 | 5077 | 0.28405475 | -13.9 | 藤原 |
| 8.0 | 1795 | 0.2312003 | -30.6 | 森島 |
| 10.0 | 752 | 0.1612725 | -51.6 | 森島 |
ヤング率7500N/mm2 ポアソン比0.4 理論値0.3333
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.5 | 394121 | 6.57938 | -1.4 | 君島 |
| 0.7 | 130916 | 6.4781 | -2.8 | 君島 |
| 0.8 | 72101 | 6.43695 | -3.5 | 髙橋 |
| 0.9 | 71718 | 6.43136 | -3.6 | 髙橋 |
| 1.0 | 72278 | 6.44302 | -3.4 | |
| 1.2 | 65575 | 6.408255 | -3.9 | 田村 |
| 1.4 | 41096 | 6.316155 | -5.2 | 田村 |
| 1.5 | 23417 | 6.120905 | -8.2 | 根本 |
| 1.8 | 11758 | 5.7368975 | -13.9 | 根本 |
| 2.0 | 11817 | 5.7382525 | -13.9 | 藤原 |
| 4.0 | 2862 | 4.9428 | -25.9 | 藤原 |
| 8.0 | 897 | 4.0411725 | -39.4 | 森島 |
| 10.0 | 596 | 3.4634575 | -48.1 | 森島 |
ヤング率6000N/mm2 ポアソン比0.4 理論値6.67