斉藤輝の卒論日誌

タッチタイピング記録†

ccx座屈荷重とオイラー座屈荷重†

正方形断面、単純支持としてオイラー座屈荷重を求める。 詳しい寸法はf90ファイルの中にあります。

正方形断面†

3点曲げ†

細長比138.5640

Pcr=4.2357E-002

ccxでは単純支持は中立軸に線拘束、 載荷点は一面載荷にする。

• 単純支持を線拘束でなく断面一面拘束してしまうとおかしい値になる

• 支点からはみ出すモデルがよいかどうか比較

  	支点から少しはみ出す	支点からはみ出さない
  n次モード	座屈荷重（MN)
  1	0.4246390E-01	0.4245872E-01
  2	0.8387729E-01	0.7136013E-01
  3	0.1688250E+00	0.1687385E+00
  4	0.2461169E+00	0.2113951E+00
  5	0.3760653E+00	0.3755901E+00

2次モードで座屈荷重が違う。。

• 単純支持で端部を支点から少し飛び出すモデル &link(kouoz1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/kouoz1.f90)
• 端部が支点から飛び出さないモデル &link(ifkou1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/ifkou1.f90)

3点曲げの半解析†

片方中立軸にローラーを線でいれる、 スパンを半分にした断面すべてでz方向拘束

• x方向拘束なし

  n次モード

  座屈荷重（MN)

  1	0.4242539E-01
  2	0.4246346E-01
  3	0.3755969E+00
  4	0.3760319E+00
  5	0.1010655E+01

総荷重1MNを分配してccxで出てきたBUCKLINGの値をそのまま読めて、 そのまま読んだ値が3点曲げ解析の座屈荷重やオイラー座屈荷重と近い。 1次モードはかなり近い値になるが、2次モードからは違う値になる。 x方向の拘束なしでやってるけど入れられるところはあるのでしょうか。 &link(kouzahan2.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/kouzahan2.f90)

長方形断面†

• ( b=3.2d-2!幅 h=2.0d-2!高さ
• ) くらいの長方形断面にしてみる。

細長比138.5640 オイラーの座屈荷重\( Pcr=6.777E-002 \)

やはり1次モードでは同じような値が得られるが、2次モードから違う値が出る。 座屈挙動を確認してみると3点曲げモデルでは1次,2次共にy方向に座屈がおこる。 半解析モデルでは、1次はy方向に座屈が起こっているが、 2次モードではx方向に座屈してしまっている。

ccxで座屈解析をして式の値と比較するときは、cgxで想定した方向に座屈しているか、全部のモードでちゃんと確認したほうがいいと思う。

gnuplotで線形回帰†

例えばkaiki.txtに、ひずみ-応力　のように並べて、

• ( set term png set output 'hoge.png' f(x)=a*x+b fit f(x) 'tate' using 1:2 via a,b plot 'tate' pt 2,f(x) w l
• ) と書いて、コマンドラインで
• ( gnuplot<kaiki.txt
• )

yang.f90,syokignu2.f

鉄の引張 片持ち梁(弾性、弾塑性解析)†

• 鉄の種類:SS400
• 降伏応力:235N/mm^2 －鉄の寸法
  • 長さ:1m
  • 幅:10cm
  • 高さ:10cm
  • ヤング率E=206GPa
  • ポアソン比ν=0.3
• 断面積:100cm^2=10000mm^2
• 分割数：nx=128,ny=10,nz=10

calc†

節点荷重での解析(断面一様分布)

弾性解析†

弾塑性解析†

• ( print'("*DEFORMATION PLASTICITY")' print'("206.E3,0.3,235.,1.,0.2")'
• ) Exponent(n)を変えてみる。(式中の指数) DEFORMATION PLASTICITYについては&link(柴田さんの修論日誌,http://www.str.ce.akita-u.ac.jp/kako/j2011/shibata.html#i86)を参照。 datの中で各荷重段階にあわせてtimeごとに変位が出力される。

• n=1

  応力(MPa)	軸方向変位最大値(m)
  10	6.109180E-05
  50	3.056134E-04
  100	6.115850E-04
  150	9.179159E-04
  190	1.163240E-03
  200	1.224603E-03
  210	1.285988E-03
  220	1.347380E-03
  230	1.408793E-03
  235	1.439502E-03

mentat弾塑性解析†

面荷重での解析

• 解析モデル

  応力(MPa)	軸方向変位最大値(m)	ひずみ	ヤング率(GPa)
  50	2.420E-4	2.420E-4	206.6
  100	4.839E-4	4.839E-4	206.7
  150	7.259E-4	7.259E-4	206.6
  200	9.681E-4	9.681E-4	206.6
  230	1.114E-3	1.114E-3	206.5
  235	3.234E-3	3.234E-3

• 応力とひずみの関係(縦軸:応力　横軸:ひずみ)

hariw.fの使い方†

• (

  #倍率0のままで要素数、断面諸量などを適時変えて oir.fコンパイル実行

./oir#1つのoiraa.dができる ./hariw<oiraa.d #1つのfort7とfort11とuvw.outができる ./modo2#fort7を読み込んでモード計算。modoが7個できる(ゴミの外乱)

#oir2.fの倍率、弧長、弧長増分を適時変えてコンパイルして実行 ./oir2#oir001～oir010まで倍率を変えてファイルができる

chmod 744 job ./job#oir001～010まで自動で読み込んで設定反復回数を終えると自動で止まる

• )

3点曲げの半解析†

• b=1cm,h=1cm,ell=50cmの鋼材の三点曲げ。荷重P=100N。
• 荷重は支間中央部に線載荷する。半解析モデルでも線載荷とする。
• ヤング率206GPa,ポアソン比0.3
• C3D8要素、nx=ny=10,nz=600

片方ヒンジ、片方ローラー†

3点曲げモデルたわみ†

• 拘束条件を簡略化 ヒンジ部分幅方向(x方向)に全てxyz=0 ローラー部分x方向に全てxy=0 支間中央線載荷

  		相対誤差(初等梁)	相対誤差(ティモ)
  最大値(m)	1.512610e-03	0.289%	0.413%
  中央載荷部断面平均(m)	1.51235E-03	0.306%	0.430%

  • mentatで解く 最大値1.519(mm)

• 拘束条件を理想的に ヒンジ部分x方向の真ん中(b/2)だけxyz=0、他はyz=0 ローラー部分x方向の真ん中だけ(b/2)xy=0,他はy=0

  最大値(m)	中央載荷部断面平均(m)
  1.512610e-03	1.51235E-03

片持ちとして解く†

ell/2=25cm,荷重P/2=50N 自由端に線載荷

半解析†

ell/2=25cm,荷重P/2=50N

片方ローラー、もう片方の断面をz方向拘束、断面の真ん中(x=b/2)だけx方向拘束

両方ヒンジ†

3点曲げモデルたわみ†

• 拘束条件を簡略化 ヒンジ部分幅方向(x方向)に全てxyz=0 支間中央線載荷

  最大値(m)	中央載荷部断面平均(m)
  6.910970e-04	6.90936E-04

• mentatで解く 最大値6.978e-1 (mm)

• 拘束条件を理想的に ヒンジ部分x方向の真ん中(b/2)だけxyz=0、他はyz=0

  最大値(m)	中央載荷部断面平均(m)
  6.914600e-04	6.91299E-04

半解析†

ell/2=25cm,P/2=50N 片方ヒンジ、もう片方は断面一面z=0で、b/2の部分だけxz=0

各種モデル最新版†

プレストレス木箱桁橋片持ち箱断面モデル†

&link(onsi14.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/model/onsi14.f90)

プレストレス木箱桁橋片持ち補剛材ありモデル†

&link(onsih14.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/model/onsih14.f90)

プレストレス木箱桁橋片持ち箱断面上部鋼板欠けモデル†

&link(onsikake.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/model/onsikake.f90)

調査用プログラム†

c3d6要素で直方体を作るプログラム†

一気にinpを作る†

&link(ifc3d6.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/model/ccxtyousa/ifc3d6.f90)

• 1つのinp作る &link(c3d6t.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/model/ccxtyousa/c3d6t.f90)

c3d8要素で直方体を作るプログラム†

c3d8要素で一気にinpを作る†

&link(ifc3d8.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/model/ccxtyousa/ifc3d8.f90)

unv→inp変換プログラム†

大体プレストレス木箱桁橋用に特化してる

3点曲げ†

&link(3tenc3d4unv.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/prog/3tenc3d4unv.f90)

半解析†

&link(hanc3d4unv.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/2014/prog/hanc3d4unv.f90)

d4d6d8unv.f90†

• c3d4,c3d6,c3d8要素に対応。 要素が混在してると、unv内でどこでどの要素が出てくるか、というのはモデルによって違ってくるので、要素の種類ごとに適当な名前の一時ファイルを作ってそこに要素の情報をいれといて、あとでそこから拾ってくるという方式にしてます。 &link(d4d6d8unv.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/d4d6d8unv.f90)

• 押し出しによるメッシュの作成の例を試したかったため作成

• 参考 http://www.geocities.jp/penguinitis2002/study/Salome/extrusion/extrusion.html

計算用プログラム†

• 等方性材料片持ち梁の理論値計算確認用(&link(keitouhou.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/keitouhou.f90))

• 異方性材料(木材)片持ち梁の理論値計算確認用(&link(keimoku.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/keimoku.f90))

課題†

PCゼミ14/6/16†

パソコンゼミ14/5/26†

• mokuzai.f90 をコンパイルして、実行して出てくるテキストあるいはファイルに書きこませたテキストの、
  • ( ～～

ELASTIC,TYPE=ORTHO　←ここから†

～～ ～～ ～～ ←ここまで (要は、*SOLID SECTION の一行上まで)

SOLID SECTION,ELSET=Eall,MATERIAL=mokuzai†

• ) をコピーし、inpファイルの中身の
• (

ELASTIC†

ヤング率、ポアソン比 

• ) という部分を消して、その部分に貼り付ける。

• 片持ち梁の理論値計算確認用(&link(kei14.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/kei14.f90))

正方形断面の木材　片持ち梁†

12cm × 12cm 断面の木材、荷重100N,k=5/6　とする。 ヤング率7.000GPA,直行異方性の木材として片持ち梁で解く。 (&link(ifyousoz.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/sotu/ifyousoz.f90)) で長さを30cm～500cmまで10cmずつ変えてたわみの平均を取る。 C3D8要素とする。 要素分割はx=10,y=10,z=600とする。

• 相対誤差と長さのグラフ
  • y軸:相対誤差(%),x軸:長さ(cm)
  • 赤線:初等梁理論のたわみとFEMの相対誤差,緑線:ティモシェンコ梁のたわみとFEMの相対誤差

• せん断項とell/hのグラフ
  • y軸:せん断項/ティモシェンコ梁たわみ ,x軸:ell/h

14/5/12†

• Salomeでモデル生成、C3D8でメッシュ作成、unvをinpに変換して解いてみる ヤング率7.694GPa ,ポアソン比0.4 幅80mm、高さ40mm、長さ800mm、荷重1MN
• lengthは1つの要素の最大の長さ

  length	たわみmax(m)
  10	4.444930e+01
  7	4.444540e+01

• このモデルではlengthを2以下にすると要素数が多くなりすぎて計算できない。

正方形断面の鋼材†

断面2cm×2cm、長さ40cm, ヤング率206.0GPA,ポアソン比0.3,荷重100N

• まずccxプログラムと理論式で値を求める。 分割数はnx=10,ny=10　C3D8要素

  nz	たわみmax(m)	相対誤差(初等梁)(%)	相対誤差(ティモ)(%)	要素数
  300	7.727840e-04	0.504060	6.97700E-01	30000
  500	7.737010e-04	0.385996	5.79867E-01	50000
  1500	7.741640e-04	3.26387E-001	5.20372E-001	150000

  たわみの単位はメートル。

• salomeで作ったのを解く salomeでモデリング・unv生成、c3d4unvでinpに変換してccxで解く。 C3D4要素。

  length	たわみmax(m)	要素数	相対誤差(初等梁)(%)	相対誤差(ティモ)(%)
  40.00	9.204240e-05	128	8.81495E+01	8.81726E+01
  20.00	4.252120e-04	834	4.52540E+01	4.53605E+01
  10.00	6.051090e-04	3910	2.20922E+01	2.22438E+01
  4.000	7.095070e-04	21091	8.65097E+00	8.82876E+00
  3.000	7.111990e-04	21614	8.43313E+00	8.61134E+00
  2.000	7.560170e-04	114338	2.66281E+00	2.85225E+00
  1.800	7.553120e-04	109053	2.75358E+00	2.94284E+00
  1.599	7.552970e-04	107468	2.75551E+00	2.94477E+00
  1.300	7.596920e-04	201254	2.18965E+00	2.38001E+00
  1.100	7.705140e-04	789275	7.96319E-01	9.89394E-01
  1.000	7.706610e-04	817866	7.77393E-01	9.70505E-01
  0.900	7.706280e-04	787666	7.81641E-01	9.74745E-01
  0.770	7.706140e-04	789458	7.83444E-01	9.76544E-01
  0.700	7.706920e-04	839416	7.73401E-01	9.66521E-01
  0.600	7.724360e-04	2899514	5.48861E-01	7.42418E-01
  0.500	ERROR	6119669	allocating memory	corei5 メモリ16GBで発生

  • 現在のPCスペックでは、このモデルにおいてはlengthを0.600以下にするとメッシュ分割に時間がかかりすぎる(分割したところでccxで解ききれるかもわからない)ため、この辺りが限界。すべてC3D4でメッシュを切る場合、要素数が多くないと誤差が大きい。

卒論日誌†

プレストレス木箱桁補剛材関連†

FEMと穴開きモデルと2013/7/10、2013/2/13-14の実験との比較†

穴開きモデルは木材部分の(saika)のたわみの平均値を取った。

穴開きモデルとの比較†

補剛材あり鋼板あり穴開き†

• y軸:荷重(kN) x軸:たわみ(mm) 緑線-補剛材あり鋼板あり 青線-補剛材あり鋼板あり穴開きモデル 赤線-実験値(20130710)

補剛材なし穴開き†

• y軸:荷重(kN) x軸:たわみ(mm) 緑線-補剛材なし穴なしモデル 青線-補剛材なし穴開きモデル 赤線-実験値(20130219.補剛材なし1回目)

12/20 ccxによる有限要素解析と2/17,18の実験との比較(3点曲げ)†

FEM鋼板有り、無しと2/17,18の実験結果

• y軸:荷重(kN) x軸:たわみ(mm)

• FEMの方が固いので、座屈などの要素を取り入れて実験値に近づくかどうか
• 実際の実験で使われるような穴開きモデルを作ってccxで解析するなどが今後の課題

上のグラフに7月の実験結果も入れたグラフ

• y軸:荷重(kN) x軸:たわみ(mm)

12/17†

• y軸:荷重(kN) x軸:たわみ(mm)
  • k2のdata/tugite130218内にある以下の補剛材なしの試験データとFEMの補剛材なしを比較する
  • ( J-TEST-hs.xlsx 2/18 補剛材あり J-TEST-1.xlsx 2/19 1回目、補剛材なし J-TEST-2.xlsx 2/19 2回目、補剛材なし
  • )

データ類†

補剛材有り鋼板有りオンサイト3点曲げ座屈プログラム†

(&link(onsih3zakutu.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsih3zakutu.f90))

ccxで3点曲げで解いたもの†

ccxで荷重100kNを載荷した時のたわみ値を取得。ティモシェンコ理論値はkeionsite.f90類で取得。

• y軸:荷重(kN) x軸:たわみ(mm) 緑:補剛材有り鋼板有り 青:補剛材有り鋼板無し 紫:補剛材無し 赤:実験値

• 補剛材あり鋼板有り座屈プログラム(&link(onsih3zakutu.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsih3zakutu.f90))　

(&link(onsih3zakutu.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsih3zakutu.dat))

• 補剛材あり鋼板あり穴開き たわみ
• 9.85139050E-03

• 補剛材なし穴開き
• 1.50161441E-02

平均点は :   2.09150003E-05

• 補剛材あり鋼板有り(&link(onsih31220.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsih31220.f90))

  たわみ(m)	ティモシェンコ理論値(3点曲げ)
  6.82379538E-03	7.53422878067068914E-003

• 補剛材あり鋼板無し(&link(onsihn31220.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsihn31220.f90))

  たわみ(m)	ティモシェンコ理論値(三点曲げ)
  8.35126638E-03	8.50147390384949769E-003

• 補剛材無し(&link(onsi3ten1220.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsi3ten1220.f90))

  たわみ(m)	ティモシェンコ理論値(3点曲げ)
  8.65473226E-03	9.13542523676829851E-003

• ccxで解析したたわみ値とティモシェンコの式の理論値との比較(3点曲げ)

• y軸:荷重(kN) x軸:たわみ(mm)

ccxで片持ち梁で解いたもの (上記の3点曲げに比べてellをell/2,荷重をp/2にしたもの)†

• y軸:荷重(kN) x軸:たわみ(mm) 緑:補剛材有り鋼板有り 青:補剛材有り鋼板無し 紫:補剛材無し 赤:実験値
• 補剛材あり鋼板有り(&link(onsihogou1220.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsihogou1220.f90)) たわみ(mm) 6.87151263E-0

• 補剛材あり鋼板無し(&link(onsihnasi1220.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsihnasi1220.f90)) たわみ(mm) 7.97978882E-0

• 補剛材無し(&link(onsi21220.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsi21220.f90)) たわみ(mm) 8.60536564E-0

モデル†

補剛材あり鋼板あり†

• 剛性 118148936.16424280N・\( m^2 \)
• σ木= 5031110.0908723157 Pa (&link(keionsited1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/keionsited1.f90))にて取得

補剛材あり鋼板なし†

剛性 104664411.84623867 N・\( m^2 \)

σ木=6202551.3139656382 Pa

(&link(keionsited2.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/keionsited2.f90))にて取得

補剛材なし†

剛性 96481417.91999998N・\( m^2 \)

σ木=7774913.5449429713 Pa

(&link(keionsited3.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/keionsited3.f90))にて取得

目標†

グラフの荷重を100kNまでにする

1/17まで†

nzhaji→ある nzhaji2→ない kの解決

1/10まで†

座屈プログラム完成

12/27まで†

有限要素解析での補剛材ありなしと2/17,18の補剛材ありなしをグラフで比較する

座屈プログラムで解析

データ整理

12/20まで†

座屈プログラム

過去の実験（2/18,19)で得たデータを補剛材有り、無しと比較しグラフを描く

パソコンゼミ†

7/29†

課題:実験データからグラフを書く。※縦軸に載荷荷重をとるように

• 一例として下のグラフ
• 縦軸を載荷荷重、横軸を変位計の測定値に直してみました。

7/15†

相対誤差とh2のグラフを描く。

木材と鋼板のモデル†

• &link(onsitekata3.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/saito/onsitekata3.f90)で解析値を取得し、keionsite.f90を一部変更して理論値を取得。

• b1=1.2d-1!角材の幅
• b2=9.0d-3!鋼板の幅
• h1=9.0d-3!角材の高さ
• h2=h2+5.00d-2!鋼板の高さ
• h3=h2-h1*2!間の鋼板の高さ

• y軸:たわみ,x軸:h2[鋼板の高さ]　赤:理論値、緑:解析値

• 相対誤差とh2のグラフ
• y軸:相対誤差(%),x軸:h2(m)

どっちも鋼板のモデル†

• onsitekata2.f90で解いたデータを解析値とし、hakotakasa.f90で理論値を取得。

• b1=1.2d-1!角材の幅
• b2=9.0d-3!鋼板の幅
• h1=1.2d-1!角材の高さ
• h2=h2+5.00d-2!鋼板の高さ
• h3=h2-h1*2!間の鋼板の高さ

• y軸:たわみ,x軸:h2　赤:理論値, 緑:解析値

• 相対誤差とh2のグラフ
• y軸:相対誤差(%),x軸:h2(m)

7/1までの課題†

滝田さんのプログラムonsitekata2.f90を使い、たわみを解析してグラフ作成。 オンサイト木橋片持ち梁のモデルで、材料の寸法のh2(鋼板の高さ)を変化させてくれる。 要素分割はnz=500

• y軸:たわみ,x軸:h2

6/24までの課題†

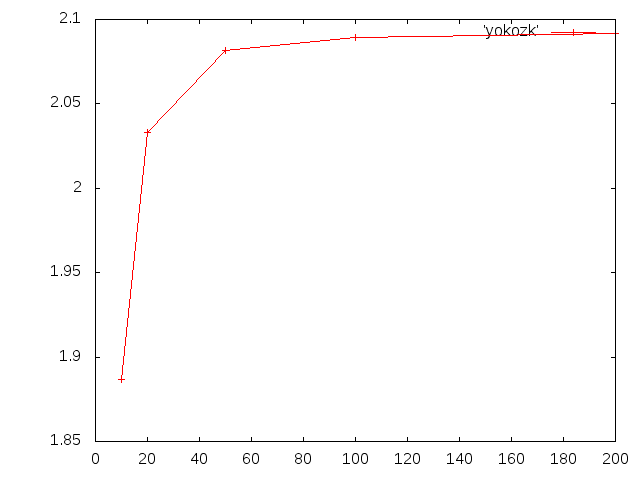
私はnx1=2,nx2=3,ny1=6,ny2=8としてnzを変えてグラフを作成

応急橋片持ち†

• y軸:たわみ(E-3),x軸:nzの分割数

オンサイト木橋片持ち†

• y軸:たわみ(E-3),x軸:nzの分割数

6/17までの課題†

荷重は1MNとする。

6/10の課題での梁断面正方形 (b=0.040m ,h=0.040m,ell=0.200mのアクリル材)のモデルを考える。

たわみの理論値は0.0042967m=4.2967mmである。

ccx_2.3で出力されるdatファイルの中の大体一番大きそうな値をたわみ値にした。

• たわみとLengthのグラフ 見やすさを考慮しx軸は反転させている。右に行くほどLengthは小さい値になる。
  • y軸:たわみ値(mm),x軸:Length
• たわみとNudesのグラフ 見づらかったので対数グラフにしました。
  • y軸:たわみ値(mm),x軸:Nudes(要素数)

---

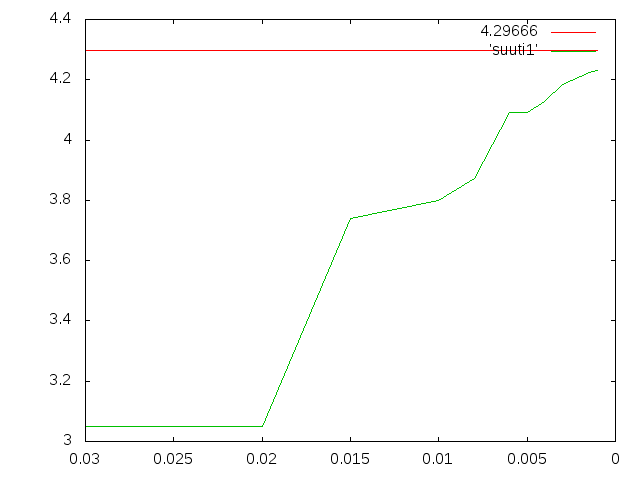
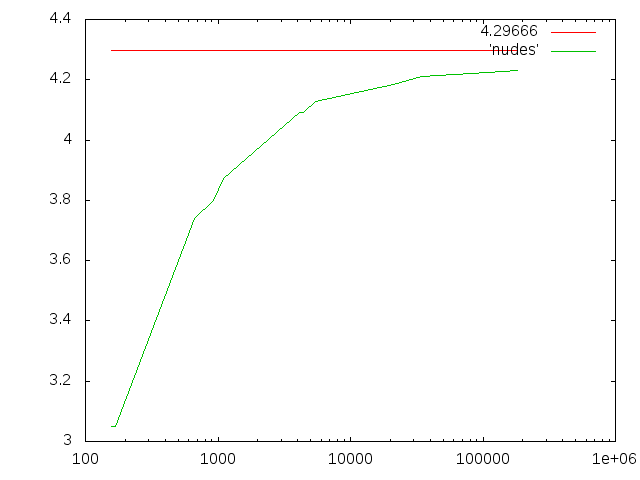
Lengthを小さくしてNudesを多くした方が理論値に近づくっぽい。 SalomeでLengthを入力するときは値が小さくなるなら2.0e-01とかのe-XXで入力する方が安心。

6/10までの課題†

b（幅）、h（高さ）、ell（長さ）とする。 また、荷重は1MNとする。

長方形（縦長）†

b=0.020m ,h=0.040m,ell=0.200mのアクリル材 せん断補正係数によるたわみを計算したたわみ＝0.008593m

• nx=10,ny=10でnzを10～200まで変化させたグラフ
• 縦軸：たわみ(mm)、横軸：nz

正方形†

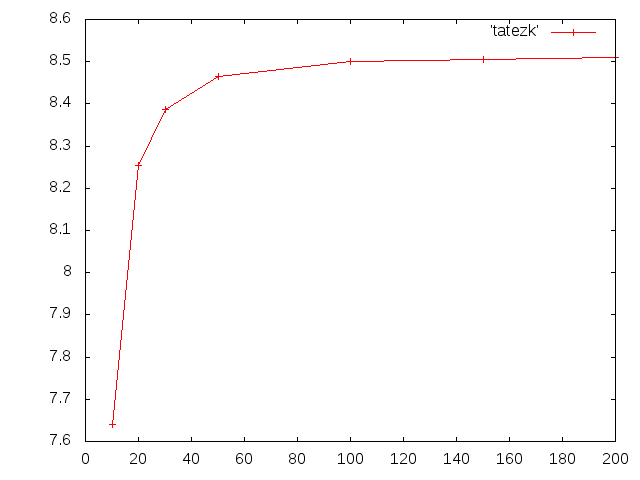
b=0.040m ,h=0.040m,ell=0.200mのアクリル材 せん断補正係数によるたわみを計算したたわみ＝0.0042967m

• nx=10,ny=10でnzを10～200まで変化させたグラフ
• 縦軸：たわみ(mm)、横軸：nz

長方形(横長)†

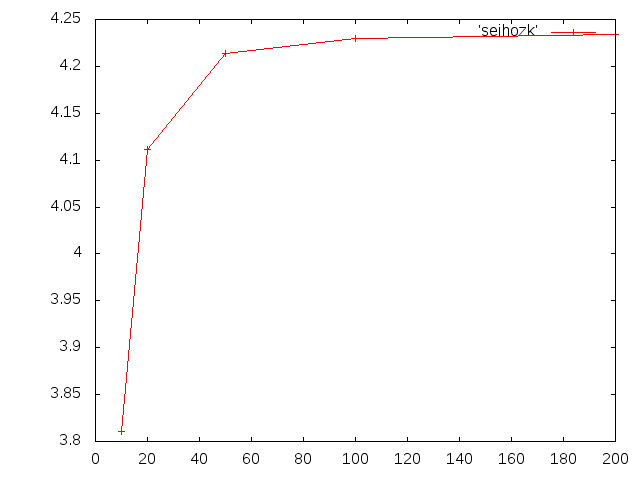
b=0.080m　,h=0.040m,ell=0.0200mのアクリル材 せん断補正係数によるたわみを計算したたわみ=0.0021483m

• nx=10,ny=10でnzを10～200まで変化させたグラフ
• 縦軸：たわみ(mm)、横軸：nz

• ny,nzを増やしたほうがたわみ値は手計算の値に近づくのではないか。しかし、ny,nzを増やしていくと計算に時間がかかり、nx=10,ny=40,nz=200以上だと私のパソコンではものすごく時間がかかるようだったので今回はnx=10,ny=10としてnzを変化させていった。

コマンド†

• ( cp /media/Transcend/150416_1.CSV ~/zikken/ vi 150416_1.CSV ./syokignu2<150416_1.CSV>140416_1s.csv gnuplot
• ) 2015年度

以下は2014年度

• ( cp /media/Transcend/140410_1.CSV ~/zikken/ vi 140410_1.CSV ./syokignu2<140410_1.CSV>140410_1s.csv gnuplot
• )

最新の100件