- 卒論日誌
- 11月15日 曲げ
- 9月30日〜 今後やること
- あ
- 6月7日 今後の課題
- 6月7日〜 グラフ
- 5月26日〜 様々な節を入れた90×90×1200mmの片側固定端
- 問題
- 5月31日 健康な状態の場合(節がないとき)
- 5月31日 正二十面体、直径10mm、1個の場合 (0mm,600mm,1200mm)
- 5月31日 円柱、直径10mm、1個の場合 (0mm,600mm,1200mm)
- 6月2日 円柱、直径30mm、1個の場合 (0mm,600mm,1200mm)
- 6月2日 円柱、直径50mm、1個の場合 (0mm,600mm,1200mm)
- 5月31日 正二十面体、直径10mm、3個の場合 (0mm,600mm,1200mm)
- 6月2日 円柱、直径10mm,30mm,50mm、3個の場合 (0mm,600mm,1200mm)
- 5月24日 今後の課題
- 5月18日〜 初期不整を導入した90×90×1200mmの片側固定端
- 5月17日 今後の課題
- 5月12日〜 90×90×1200mmの片側固定端
- 5月10日 今後の課題
- 4月21日〜 200×200×2600mmの単純梁
- エラー
- 弾塑性解析方法(バイリニア型)
- 作業日誌
- 春休みの課題
卒論日誌†
11月15日 曲げ†
11月15日 弾塑性解析 曲げ 間違い†
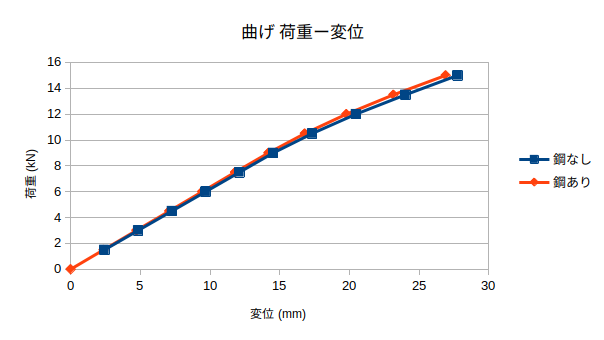
- 100×60×1200mmの木材梁で曲げ解析を行った。(今度行う実験の梁と一緒の寸法のもの)
- 鋼材は直径16mmの丸形のものを入れた。(これも実験と同じもの)
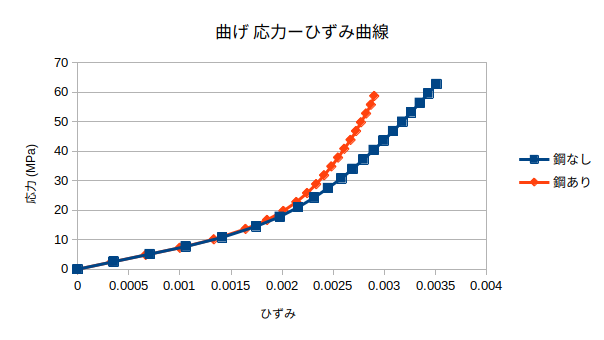
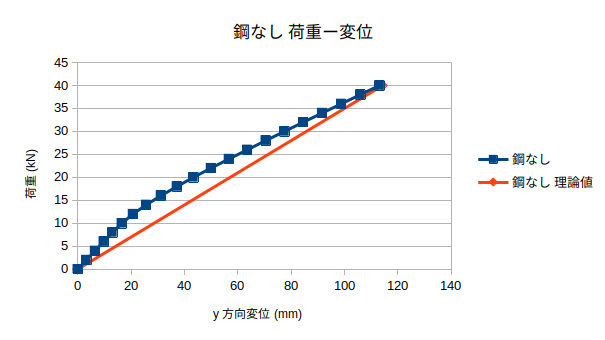
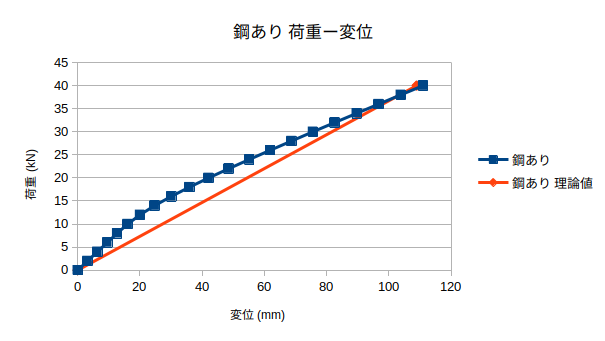
- 解析結果をもとに、応力ーひずみ曲線と荷重ー変位グラフを作成した。
- 変位の相対誤差は、鋼なし鋼あり一番大きいところで−38%程度だった。

11月29日 弾塑性解析 曲げ 訂正†
- 前回の応力ーひずみ曲線は間違えていたので、正しいものにした。
- 31MPaのところで降伏するように設定したので、きちんと弾塑性解析が行えている。
- 式から求めた推定最大荷重は6.75kNとなった。
- 解析結果では、10kNあたりから傾きはじめているが、なぜずれているのか自分ではよく分かってない…
- 鋼ありとなしでは、1mm程度変位の違いがあった。
9月30日〜 今後やること†
- 弾塑性解析をやる。
- まずは、何もない梁で実験値と同じくらいの解析ができたら、節とか鋼材を入れていく。
- 節の周りのヤング率を変えていく?←これも弾塑性
- 参考→Salome-Meca演習_弾塑性解析
10月1日 弾塑性解析 シンプルなやつ†
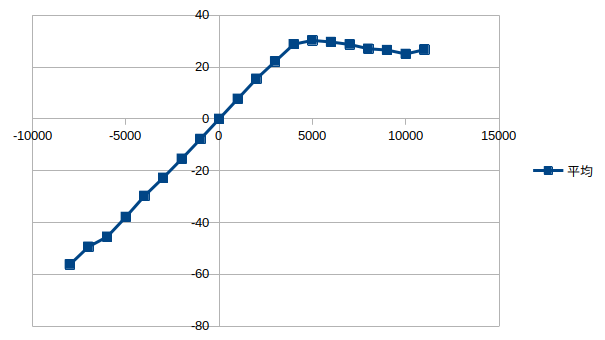
- 90×90×1200mmのシンプルな木材梁で弾塑性解析をやってみた!等方性材料
- 下の図は薄木先生の実験値、実験のグラフのような塑性の間右下がりになるような解析はできないっぽい?
- 「Function and Lists」の「Define function」の座標設定で、座標(0.005,31),(0.01,27)にしてたらずっとエラーが出てた。
- 座標を(0.005,31),(0.01,31)にしたら解析できたけど、線形の挙動までしか解析してくれなかった。
- 座標を(0.005,31),(0.01,32)にしたらやっと上の図みたいに弾塑性解析できた。(縦軸MPa)

10月6日 弾塑性解析 シンプルなやつ 訂正†
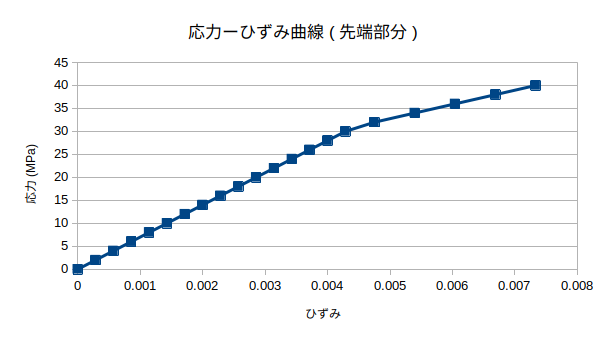
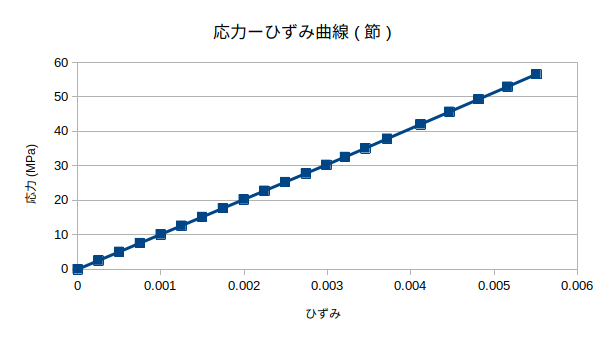
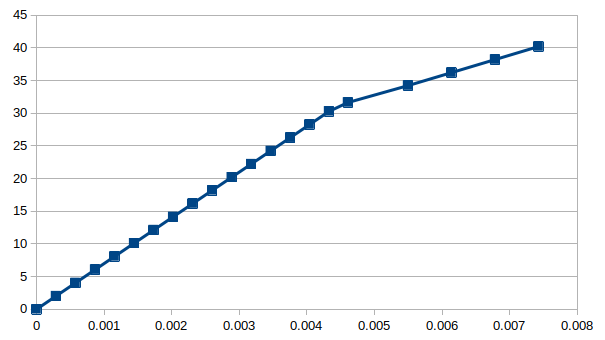
- 10月1日に載せた弾塑性解析は、グラフをよく見てみると応力が31MPaのときに降伏するように与えているのに、
- 29MPaあたりで降伏していたため、Salome-Meca演習_弾塑性解析の方法では適切な解析ができないとなった。
- AsterStudyの設定を変えてみたところ、したの図のようにうまく解析できた。
- 節に弾塑性は入れていない。
- 木材は31MPaで降伏、節の周りは20MPaで降伏するように設定した。
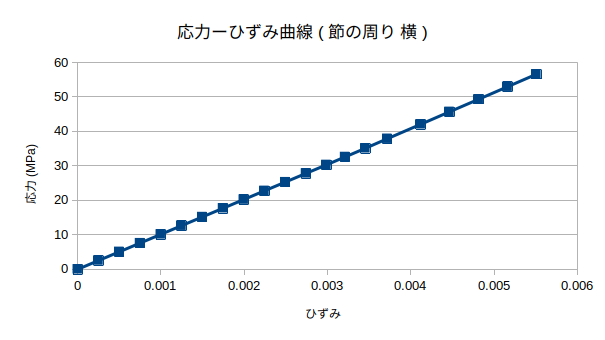
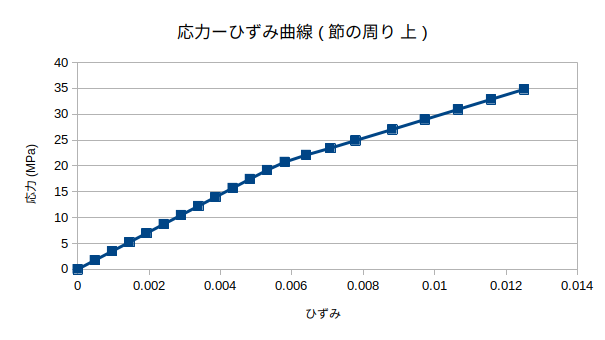
10月25日 弾塑性解析 鋼材有り†
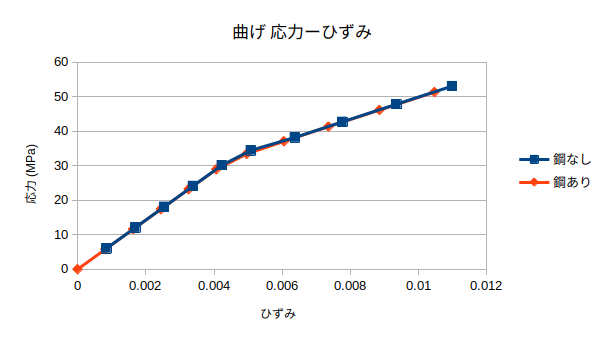
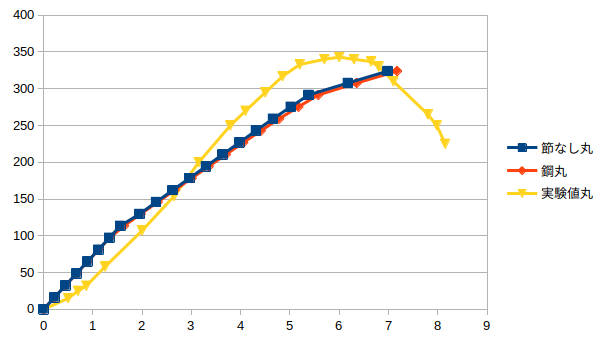
- 先週と同じ弾塑性解析の方法で鋼材を入れて解析した。
- 鋼材は16×16mmの正方形のものと直径16mmの丸形のものを入れた。
- 一番上の部分の応力ーひずみ分布は正方形も丸形も違いはなかった。縦軸:応力(MPa) 横軸:ひずみ
- 荷重ー鉛直方向変位のグラフはそれぞれ実験値に近づけることができた。縦軸:荷重(kN) 横軸:変位(mm)

7月26日 今後の課題†
- 弾塑性、圧縮と引張のやつをやる。論文を読んでスギとかの圧縮引張関係を数値化する(応力がいくつのときひずみがいくつとか)単位も変換しなければならないMPaに
- ヴォなんとかのアシンメトリー?に圧縮と引張の設定ができるらしい
- 発表10分スライドは10枚、スライド1枚につき1分は超えないようにする
6月21日 今後の課題†
- 1.木材の異方性を考慮 2.固定端の方法を変える(x,yのやつ) 3.中に鉄筋を入れる
6月7日 今後の課題†
- 節(円柱)の解析結果より、座標が(0,0,0~1200)と(90,0,0~1200)のときのy方向への変位をグラフにしてみる。
6月7日〜 グラフ†
- z軸が0~1200mmのときのy方向への変位をグラフにしてみる。
- グラフにしたとき、z軸の0に近い方の変位を無くすためにポアソン比を0.001にして解析を行う。
- 直径10mm、30mm、50mmの節のとき、それぞれ節の周りの仮想材料は2mm、5mm、10mm、15mmにする。
- (直径50mmのときは節の周りを2mmにしてしまうとメッシュが大きくなりすぎるためできなかった。)
グラフ†
6月21日 節(直径50mm)†
6月16日 節(直径30mm)†
6月21日 節(直径10mm)†
6月10日†
直径30mm、1個、一番下†
直径30mm、1個、真ん中†
直径30mm、1個、一番上†
直径30mm、3個†
5月26日〜 様々な節を入れた90×90×1200mmの片側固定端†
- 90×90×1200mmの梁で片方を固定端にして、もう片方の自由端からZ方向に荷重をかけたときの縮みを求める。
- 最初は、節の形を正二十面体にして( E(木)=7500N/mm^2 , E(節)=3750N/mm^2 )解析を行っていたが、
- 途中から、”本来、節はヤング率は少し硬くなっていて、節の周りのヤング率が柔らかくなっているため節から折れているように見える”という助言を頂いたので、節の形を解析しやすい円柱の形に変更して解析を行った。
- 節の周り2mmのヤング率を半分にして柔らかさを表現した(?)。このとき、E(木)=7500N/mm^2 , E(節)=10000N/mm^2 , E(節の周り)=3750N/mm^2
- (メッシュの関係で直径50mmのときは節の周りを5mmにした)
- 健康な状態の梁(節がない状態)と比較を行う。
- 正二十面体は半分を埋め込み、円柱は長さ(奥行き?)45mmにして、梁の半分の長さを埋め込んだ。
- 不整を与えていない梁なのに、y方向の変位がマイナスの値になるのはおかしい
- 90*90*1200mmの梁で、400kNかけたときの y方向変位→-0.011859319mm
- 45*45*600mmの梁で、400kNかけたときの y方向変位→0.001535808mm
- 90*90*600mmの梁で、400kNかけたときの y方向変位→-0.005545171mm
- 10*10*100mmの梁で、400kNかけたときの y方向変位→0.020612072mm
- 100*100*1000mmの梁で、400kNかけたときの y方向変位→0.000434075mm
- 様々な場合で解析を行ったが、y方向の変位が0になることはなかった。
- ParaViSで4隅を見たときに(下図)、すべてマイナスの値になっているわけではなくプラスになっている値もあるので、潰れるように変形しているとわかる。
- →マイナス側に傾いている訳ではなさそうなので誤差なのでは?
5月31日 健康な状態の場合(節がないとき)†
- 400kNかけたときの y方向変位→-0.011859319mm z方向変位→7.865609484mm
5月31日 正二十面体、直径10mm、1個の場合 (0mm,600mm,1200mm)†
- 位置は大体z方向から0mm,600mm,1200mmの位置に節を配置して、それぞれ解析を行った。
- 条件は、E(木)=7500N/mm^2 , E(節)=3750N/mm^2
- z方向から0mmのとき
- 400kNかけたときの y方向変位→0.021984905mm z方向変位→7.866027282mm
- z方向から600mmのとき
- 400kNかけたときの y方向変位→0.009561058mm z方向変位→7.866152222mm
- z方向から1200mmのとき
- 400kNかけたときの y方向変位→-0.010564788mm z方向変位→7.866239187mm
- それぞれ健康な梁と比較したときのグラフ 横軸:変位(mm) 縦軸:荷重(kN)
- z方向
- y方向
5月31日 円柱、直径10mm、1個の場合 (0mm,600mm,1200mm)†
- 位置は大体z方向から0mm,600mm,1200mmの位置に節を配置して、それぞれ解析を行った。
- 条件は、E(木)=7500N/mm^2 , E(節)=10000N/mm^2 , E(節の周り)=3750N/mm^2
- z方向から0mmのとき
- 400kNかけたときの y方向変位→0.028714387mm z方向変位→7.866598472mm
- z方向から600mmのとき
- 400kNかけたときの y方向変位→0.008639673mm z方向変位→7.866546079mm
- z方向から1200mmのとき
- 400kNかけたときの y方向変位→-0.00989655mm z方向変位→7.866347956mm
- それぞれ健康な梁と比較したときのグラフ 横軸:変位(mm) 縦軸:荷重(kN)
- z方向
- y方向
6月2日 円柱、直径30mm、1個の場合 (0mm,600mm,1200mm)†
- 位置は大体z方向から0mm,600mm,1200mmの位置に節を配置して、それぞれ解析を行った。
- 条件は、E(木)=7500N/mm^2 , E(節)=10000N/mm^2 , E(節の周り)=3750N/mm^2
- z方向から0mmのとき
- 400kNかけたときの y方向変位→-0.052589886mm z方向変位→7.863605mm
- z方向から600mmのとき
- 400kNかけたときの y方向変位→-0.011125045mm z方向変位→7.864078413mm
- z方向から1200mmのとき
- 400kNかけたときの y方向変位→-0.113038044mm z方向変位→7.861739325mm
- それぞれ健康な梁と比較したときのグラフ 横軸:変位(mm) 縦軸:荷重(kN)
- z方向
- y方向
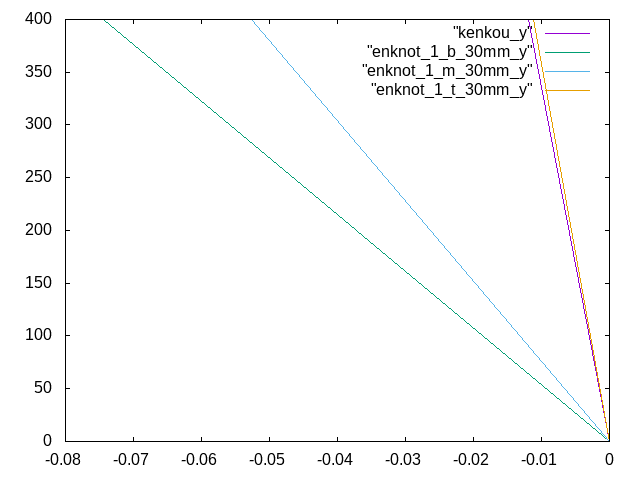
- なぜか、z方向から600,1200mmのものは健康な状態のものよりもマイナス方向に傾いていた。
6月2日 円柱、直径50mm、1個の場合 (0mm,600mm,1200mm)†
- 位置は大体z方向から0mm,600mm,1200mmの位置に節を配置して、それぞれ解析を行った。
- 条件は、E(木)=7500N/mm^2 , E(節)=10000N/mm^2 , E(節の周り)=3750N/mm^2
- z方向から0mmのとき
- 400kNかけたときの y方向変位→-0.434515111mm z方向変位→7.855726825mm
- z方向から600mmのとき
- 400kNかけたときの y方向変位→0.056822458mm z方向変位→7.868742897mm
- z方向から1200mmのとき
- 400kNかけたときの y方向変位→-0.004944817mm z方向変位→7.869329107mm
- それぞれ健康な梁と比較したときのグラフ 横軸:変位(mm) 縦軸:荷重(kN)
- z方向
- y方向
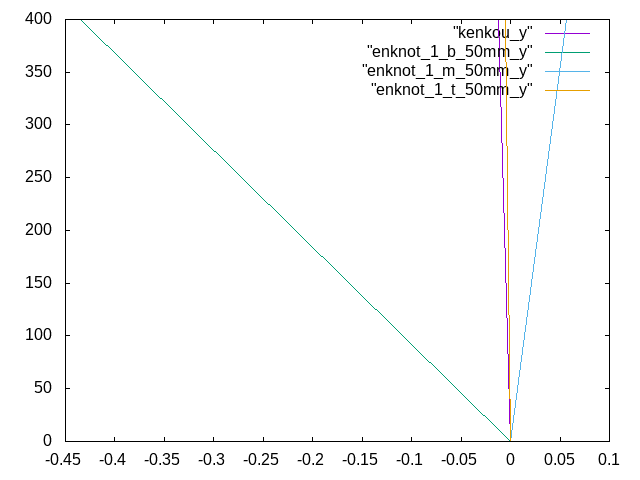
- z方向から0mmのものが健康な状態のものよりマイナス側に傾いていた。
5月31日 正二十面体、直径10mm、3個の場合 (0mm,600mm,1200mm)†
- 位置は大体z方向から0mm,600mm,1200mmの位置に節を配置して、解析を行った。
- 条件は、E(木)=7500N/mm^2 , E(節)=3750N/mm^2
- 400kNかけたときのy方向変位→0.008144219mm z方向変位→7.863364196mm
- 健康な梁と比較したときのグラフ 横軸:変位(mm) 縦軸:荷重(kN)
- z方向
- y方向
6月2日 円柱、直径10mm,30mm,50mm、3個の場合 (0mm,600mm,1200mm)†
- 位置は大体z方向から0mm,600mm,1200mmの位置に節を配置して、解析を行った。
- 条件は、E(木)=7500N/mm^2 , E(節)=10000N/mm^2 , E(節の周り)=3750N/mm^2
- 直径10mmで、400kNかけたときのy方向変位→-0.180033888mm z方向変位→7.857499206mm
- 直径30mmで、400kNかけたときのy方向変位→-0.113038044mm z方向変位→7.861739325mm
- 直径50mmで、400kNかけたときのy方向変位→0.148911072mm z方向変位→7.869329107mm
- 健康な梁と比較したときのグラフ 横軸:変位(mm) 縦軸:荷重(kN)
- z方向
- y方向
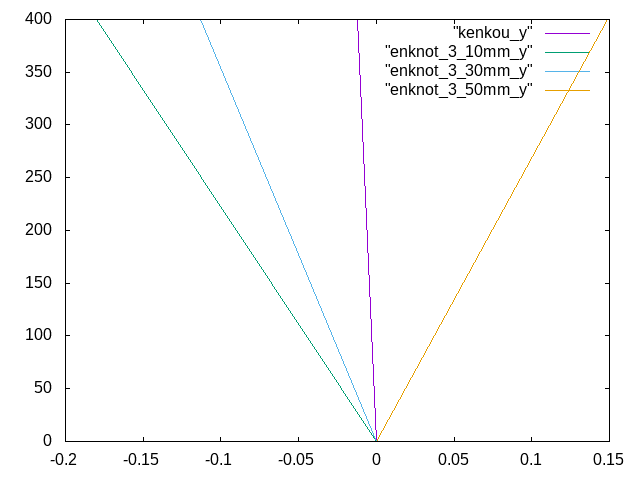
- 直径10mm,30mmのものは、健康な状態のものよりマイナス側に傾いていた。
5月24日 今後の課題†
- 90×90×1200mmの梁で節の大きさ、位置、数を変え解析を行う。
- 正二十面体を節と見立てて、大きさは直径10mm,30mm,50mm,(20mm),(40mm)、数は1個,3個,5個,(7個)とする。()は余裕があったら。
- 位置は大体z方向から0mm,300mm,600mm,900mm,1200mmの位置に節を配置する。
- 平行して、私の研究と同じような(似ている)論文がこの世にあるのか調べる。(英語でも日本語でも調べる。)
5月18日〜 初期不整を導入した90×90×1200mmの片側固定端†
- 90×90×1200mmの梁で片方を固定端にして、もう片方の自由端からZ方向に荷重をかけたときの縮みを求める。
- 比較するグラフは青木さんに貰った資料 "Composite timber-steel encased columns subjected to concentric loading" の中にあるグラフ
5月18日 ①初期不整なしの場合†
- 条件は、E=7500N/mm^2 ν=0.4 (木材)
- メッシュは5で切って、要素数は244700
- p17のP12-bare-CA(b),P12-bare-CA(c),D12-bare-CA(d)と比較をしたときのグラフは↓ 横軸:変位(mm) 縦軸:荷重(kN)
- (bare=木材の中に何も入れていない状態、CA=接着剤が2つの木材ケーシング?界面の間にのみ塗布されているという意味、P12=90×90mmの断面、D12=95×92mmの断面)
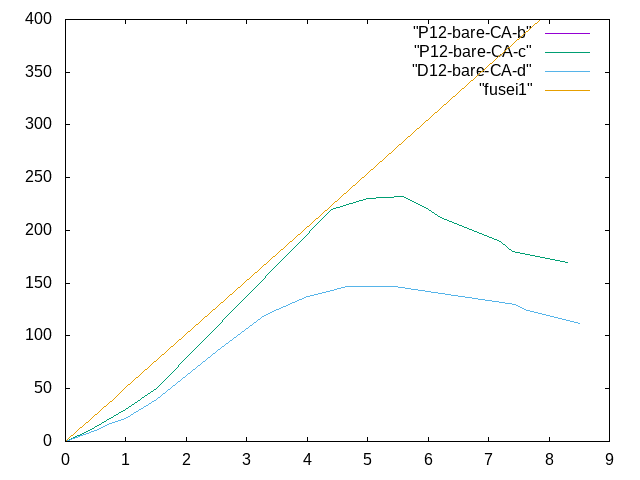
- 400kN荷重をかけたときの曲がり具合
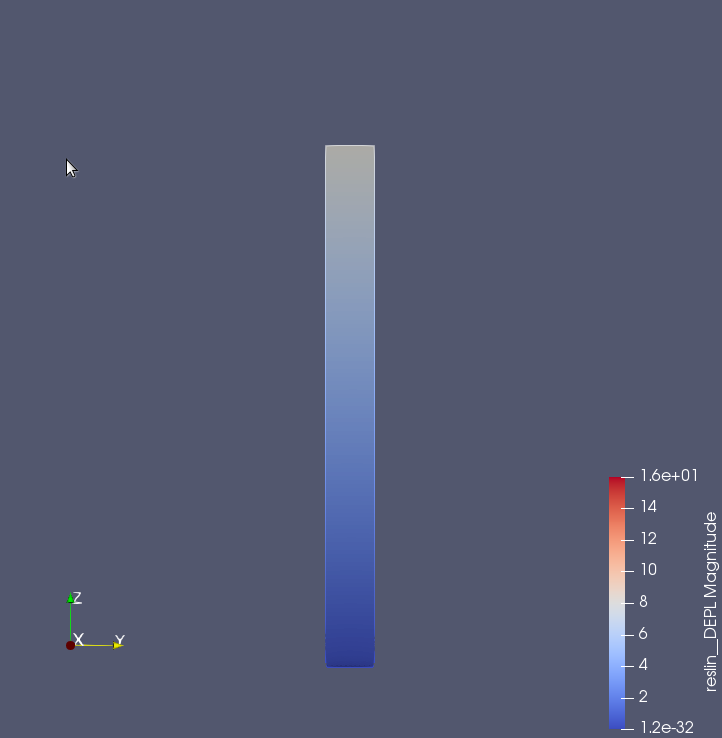
5月21日 ②上面と下面の面積を変えた場合†
- 条件は、E=7500N/mm^2 ν=0.4 (木材)
- 上面は90×90mmの正方形で、下面は88×88mmの正方形 z方向の長さは1200mm
- メッシュは5で切って、要素数は241452
- p17のP12-bare-CA(b),P12-bare-CA(c),P12-bare-CA(d)と比較をしたときのグラフは↓ 横軸:変位(mm) 縦軸:荷重(kN)
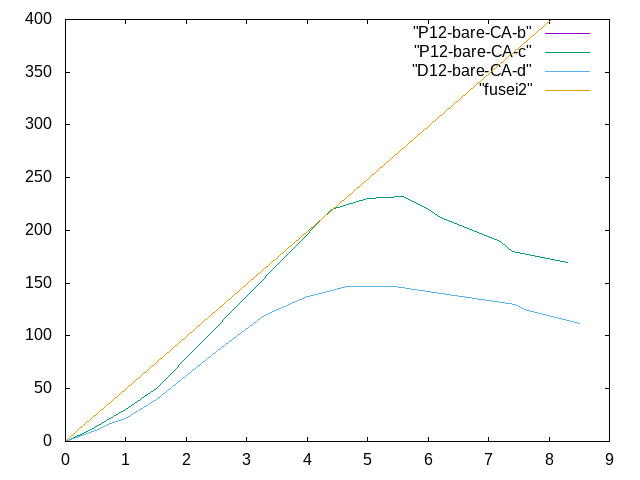
- 400kN荷重をかけたときの曲がり具合

5月21日 ③上面の位置をずらした場合†
- 条件は、E=7500N/mm^2 ν=0.4 (木材)
- 90×90×1200mmで、上面をy方向に45mmずらした梁を用いる
- メッシュは5で切って、要素数は234542
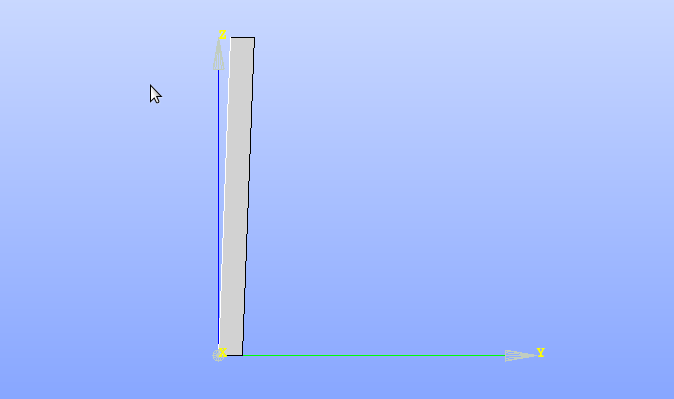
- p17のP12-bare-CA(b),P12-bare-CA(c),P12-bare-CA(d)と比較をしたときのグラフは↓ 横軸:変位(mm) 縦軸:荷重(kN)
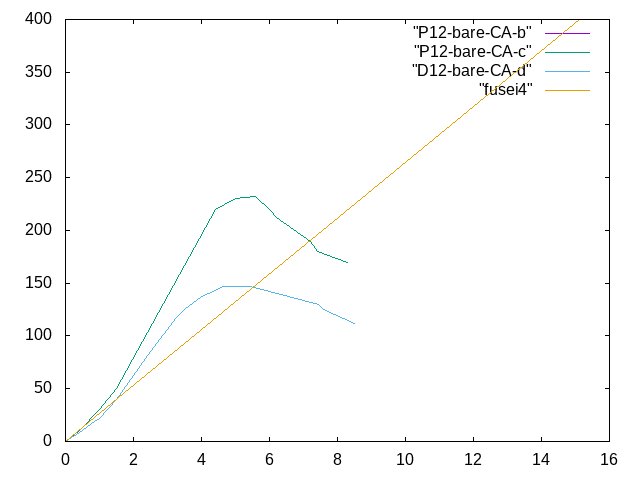
- 400kN荷重をかけたときの曲がり具合

5月21日 ④節を入れた場合†
- 最初に球でやってみたところ、エラーが出てうまくできなかった。(詳しくは目次の エラー を参照)
- そのため、球ではなく正二十面体で節を表現することにした。
- 正二十面体は一辺の長さ40mm


- p18のP12-bare-CA(1),P12-bare-CA(2),P12-bare-CA(3)と比較をしたときのグラフは↓ 横軸:変位(mm) 縦軸:荷重(kN)
- (CA(1)=節5個,平均サイズ20mm,最大サイズ25mm、CA(2)=節3個,平均サイズ14mm,最大サイズ20mm、CA(3)=節3個,平均サイズ16.3mm,最大サイズ30mm)
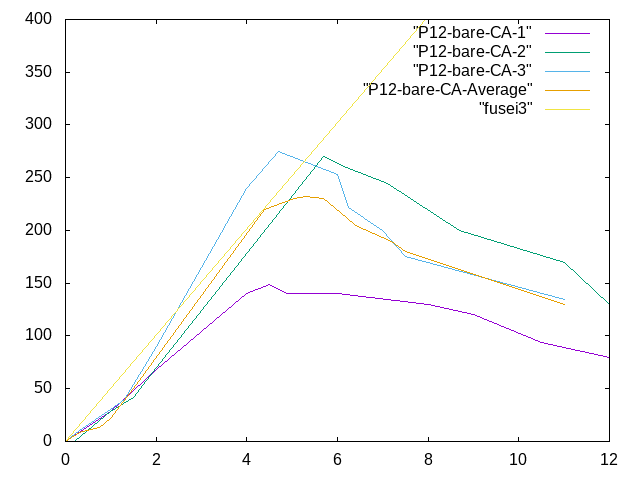
- 400kN荷重をかけたときの曲がり具合
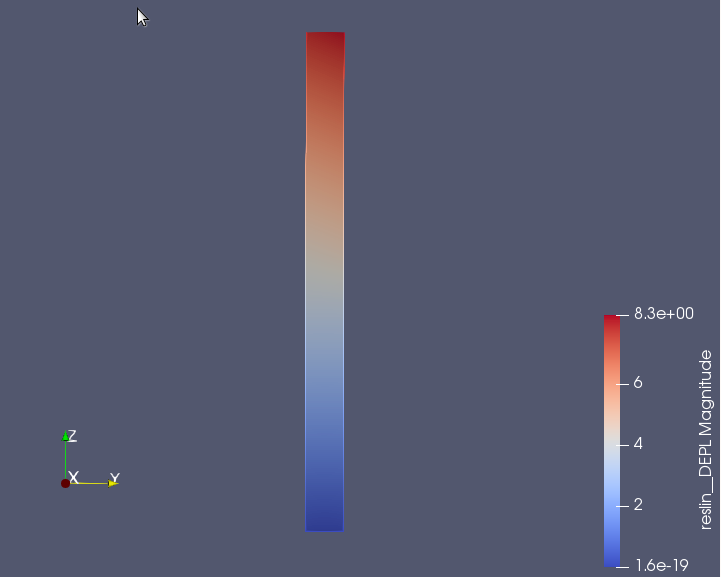
5月17日 今後の課題†
- 座屈解析は田村さんが行うので、私は初期不整を導入する方法で曲げる。
- ①初期不整なし
- ②上面と下面の面積を変えた場合
- ③上面の位置をずらした場合
- ④節を入れた場合
- 以上について400kNあたりまで荷重をかけて、400kNかけた時点での曲がり具合と、荷重-変位のグラフを求める。
5月12日〜 90×90×1200mmの片側固定端†
5月12日 90×90×1200mmの片側固定端(囲みなし)†
- 90×90×1200mmの梁で片方を固定端にして、もう片方の自由端からZ方向に荷重をかけたときの縮みを求める。
- 条件は、E=7500N/mm^2 ν=0.4 P=300kNと200kN (木材)
- メッシュは5で切って、要素数は244700
- P=300kNのとき、縮み量は載荷面の平均を求めてZ方向に -5.8992mm
- 理論値は(\( δ=\frac{PL}{EA} \))より、-5.9259mm
- 田村さんの解析の90×90×1200mmの梁の真ん中に16×16×1200mmの穴を開けた梁の縮みは -6.319215mmであったので、近い値にはなった。

- 次に、実験結果と比較をするためにP=200kNでの解析を行った。
- P=200kNのとき、縮み量は載荷面の平均を求めてZ方向に -3.9328mm
- 理論値は(\( δ=\frac{PL}{EA} \))より、-3.9506mm
- 実験結果のグラフはP=200kNのとき大体4mmほどの縮みだったので、実験結果と近い値になった。
5月13日 90×90×1200mmの片側固定端(囲みあり)†
- 90×90×1200mmの梁で片方を固定端にして、もう片方の自由端からZ方向に荷重をかけたときの縮みを求める。
- 88×88×1200mmの梁(木材)の周りを厚さ1mm鋼材で囲んだ梁を用いる。
- 条件は、P=-300kN 、E=206000N/mm^2 ν=0.3(鋼材)、E=7500N/mm^2 ν=0.4(木材)
- メッシュは5で切って、要素数は379073
- 縮み量は載荷面の平均を求めて、Z方向に -2.7507mm
- 理論値は(\( δ=\frac{PL}{EA} \))より、-2.7394mm
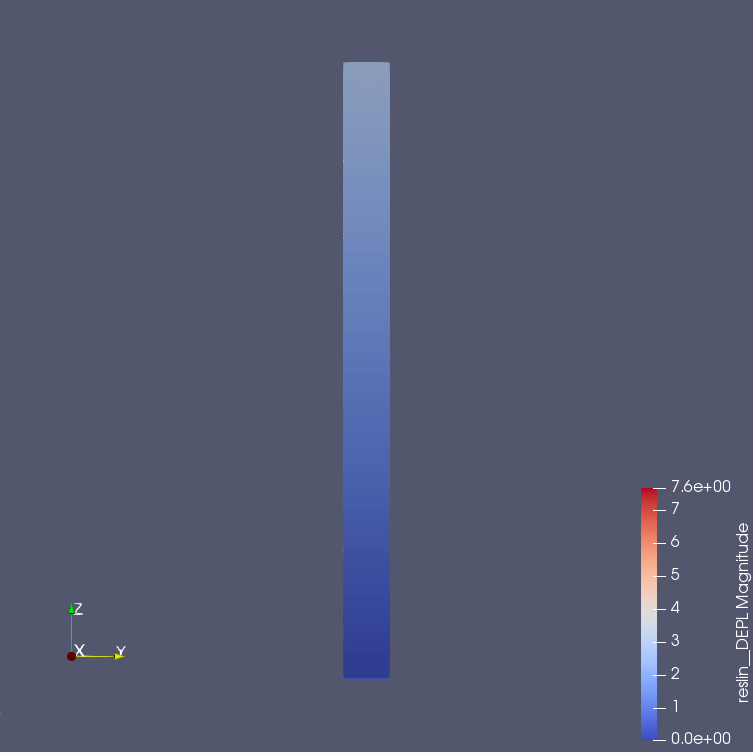
5月10日 今後の課題†
- 次は、90×90×1200mmの梁で、片方を自由端、片方を固定端にして、自由端側からZ方向に荷重をかけた場合の縮みを求める。
- 材料は木材を想定。田村さんの解析と近い値になったら、周りを1mmの鋼材で囲んだ形でもう一度解析を行う。
- 終わったら座屈解析をやってみる(難しい…)
4月21日〜 200×200×2600mmの単純梁†
4月21日 200×200×3000mmの単純梁(囲みなし)†
- Geometryで200×200×3000mmの単純梁モデルを作成した。
- ノートパソコンではなくなったのでCutを用いる方法で作ってみた。
- なぜか分からないがMeshの切り方がうまくいかず、どれだけ待っても進まなかった。
- メッシュの計算をキャンセルを押したところ、要素数が多すぎるみたいな表示が出てきた。
- メッシュの最大サイズを3000にしたときにメッシュを計算することは不可能と出てきた。なぜ(TT)
- →カットした穴の大きさの問題なのでは?と及川さんに助言してもらった。次はカットの穴を200×0.1×0.2mmではなく、200×1×2mmくらいでやってみたいと思う。
4月27日 200×200×3000mmの単純梁(囲みなし)†
- とりあえず、穴を開けない方法で鉄の単純梁中央のたわみを求めた。
- E=206000N/mm^2 ν=0.3 P=1000kN のとき
- 中央(載荷線)のたわみの平均は13.4314mmとなった。
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は20.4794mmとなった。
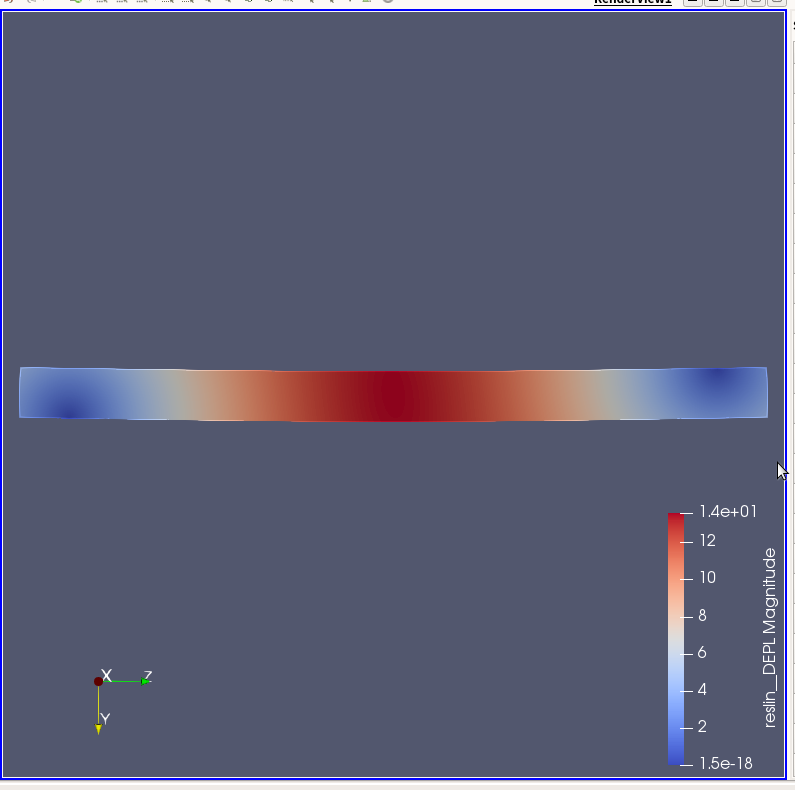
- 次に、木材の単純梁中央のたわみを求めた。
- E=7500N/mm^2 ν=0.4 P=1000kN のとき
- 中央(載荷線)のたわみの平均は367.822mmとなった。
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は562.5mmとなった。
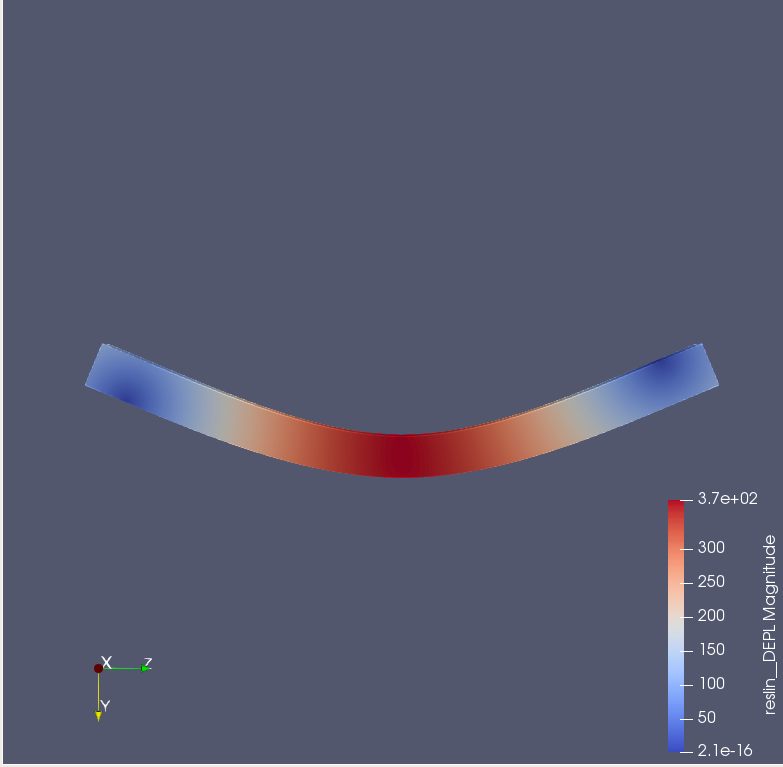
- 次は囲み(2mmくらい)ありの状態で計算を行いたいと思う。
4月28日 200×200×2600mmの単純梁(囲みなし) 昨日の訂正!!†
- 昨日の理論値は間違ってた!正しくは200×200×2600mmの単純梁だった!
- E=206000N/mm^2 ν=0.3 P=1000kN (鋼材)のとき
- 中央(載荷線)のたわみの平均は13.4314mm
- メッシュは10で切って、要素数は458140
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は13.3313mm
- E=7500N/mm^2 ν=0.4 P=1000kN (木材)のとき
- 中央(載荷線)のたわみの平均は367.822mm
- メッシュは10で切って、要素数は458140
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は366.1667mm
- 理論値に近い値になった〜!
4月28日 200×200×2600mmの単純梁(囲みあり1材料)(間違えた)†
- 穴を開けない方法で囲みありの単純梁中央のたわみを求める。
- 囲みありのときの方が要素数が少しだけ多くなった。
- 199.6×199.6×2600mmの梁の周りを0.2mmの厚さで囲んだ形の単純梁にする。↓こんな感じ。
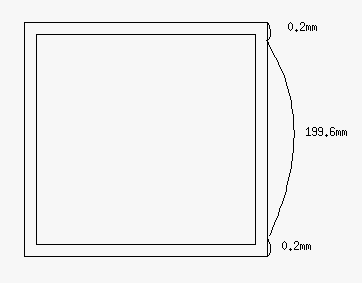
- E=206000N/mm^2 ν=0.3 P=1000kN (鋼材)のとき
- 中央(載荷線)のたわみの平均は13.43085mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は13.3313mm
- メッシュは10で切って、要素数は458588
- E=7500N/mm^2 ν=0.4 P=1000kN (木材)のとき
- 中央(載荷線)のたわみの平均は367.8057mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は366.1667mm
- メッシュは10で切って、要素数は458588
- 間違えて0.2mmでやってしまった(TT)時間がないので今度やります(TT)
5月9日 200×200×2600mmの単純梁(囲みあり1材料)†
- 前回(4月28日)囲いの厚さを0.2mmに間違えてしまった。今回はちゃんと2mmでやります。
- E=206000N/mm^2 ν=0.3 P=1000kN (鋼材)のとき
- 中央(載荷線)のたわみの平均は13.37029mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は13.3313mm
- メッシュは15で切って、要素数は341186
- E=7500N/mm^2 ν=0.4 P=1000kN (木材)のとき
- 中央(載荷線)のたわみの平均は365.79073mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は366.1667mm
- メッシュは15で切って、要素数は341186
5月9日 200×200×2600mmの単純梁(囲みあり2材料)†
- 196×196×2600mmの梁(木材)の周りを厚さ2mm鋼材で囲んだ単純梁中央のたわみを求める。
- 条件は、P=1000kN 、E=206000N/mm^2 ν=0.3(鋼材)、E=7500N/mm^2 ν=0.4(木材)
- 中央(載荷線)のたわみの平均は122.23953mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は119.87165mm
- メッシュは15で切って、要素数は341186
エラー†
5月21日†
- 球を節に見立てて解析をしようと思ったのだが、境界条件?がうまくいかないらしくエラーになってしまった。
- 収縮条件も設定しなければならないっぽい?


<S> Exception user raised but not interceptee. !
! The bases are fermees. !
! Type of the exception: error !
! !
! Solveur MUMPS : !
! La matrice est non factorisable. Elle est détectée comme étant singulière. !
! !
! Conseils : !
! - il s'agit vraisemblablement d'un problème de mise en données, vérifiez vos !
! conditions aux limites (blocage absent ou !
! surabondant) ; !
! - si le calcul est non-linéaire, rétablissez la détection de singularité !
! (paramètre NPREC à sa valeur par défaut) pour permettre !
! le découpage du pas de temps.
- 後藤さんに球ではなく長方形でやってみたらどうか、と助言を頂いたのでやってみたところできた。
- 長方形を回転させたものでも、正二十面体でもできたので球がダメだったぽい?
- 後藤さん曰く、球形にカットした梁にうまく球がはまらなかったのではないか?と言っていた。
6月2日†
- 直径50mmの節を大体等間隔に5個並べて解析を行おうと思ったらエラーになってできなかった。
- このときの節の形は円柱で、節の周り2mmを仮想材料としている。
- 仮想材料が2mmなのでメッシュを1で切ったのだが、節3個の時点で要素数が540000くらいになった。
- →要素数が大きすぎるからなのか?
弾塑性解析方法(バイリニア型)†
Material†
- ひずみと応力を設定するときに、「Function and Lists」の「Define function」の座標で与えるのではなく、
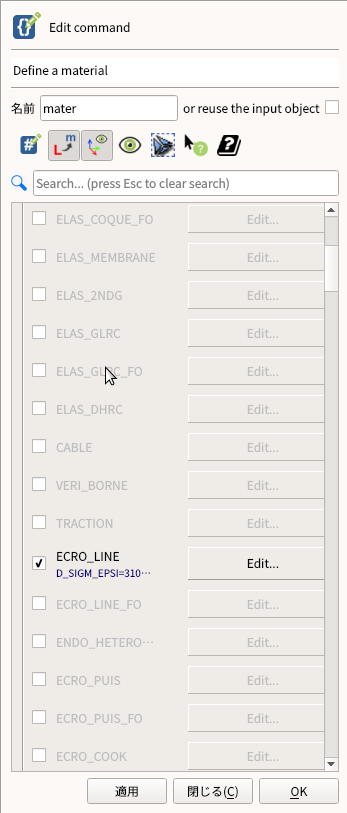
- 「Material」の「Define a material」の「ECRO_LINE」を選択する。(ヤング率、ポアソン比とかを設定するコマンドと同じでOK)
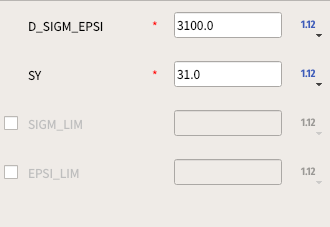
- D_SIGM_EPSI(降伏後の弾性係数(ヤング率))
- SY(降伏応力度)
Analysis†
- Materialで応力とひずみを与えるときは「STAT_NON_LINE」の「COMPORTMENT」→ + → RELATION → VIMS_ISOT_LINE にする。
\( v=\frac{P\ell^{3}}{48EI} \)
作業日誌†
| 日付 | 時間 | 作業時間 | 内容 | 立会 |
| 10/16 | 14:30-16:00 | 1.5h | 顔合わせ、ノートPCの使い方 | 後藤先生、M2、4年生 |
| 10/23 | 14:30-16:00 | 1.5h | UNIXコマンドの使い方 | 後藤さん |
| 10/30 | 14:30-16:00 | 1.5h | viの使い方 | 後藤さん |
| 11/6 | 14:30-16:30 | 2h | Salome-mecaの使い方、片持ち梁 | 後藤さん、及川さん、4年生 |
| 11/13 | 14:30-16:30 | 2h | Salome-meca、単純梁 | 後藤さん、及川さん、4年生 |
11月6日課題†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 394121 | 6.57938 | -1.4 | 君島 |
| 0.7 | 130916 | 6.4781 | -2.8 | 君島 |
| 0.8 | 72101 | 6.43695 | -3.5 | 高橋 |
| 0.9 | 71718 | 6.43136 | -3.6 | 高橋 |
| 1.0 | 72278 | 6.44302 | -3.4 | |
| 1.2 | 65575 | 6.408255 | -3.9 | 田村 |
| 1.4 | 41096 | 6.316155 | -5.2 | 田村 |
| 1.5 | 23417 | 6.120905 | -8.2 | 根本 |
| 1.8 | 11758 | 5.7368975 | -13.9 | 根本 |
| 2 | 11817 | 5.7382525 | -13.9 | 藤原 |
| 4 | 2862 | 4.9428 | -25.9 | 藤原 |
| 8 | 897 | 4.0411725 | -39.4 | 森島 |
| 10 | 596 | 3.4634575 | -48.1 | 森島 |
ヤング率:6000(N/mm^2) ポアソン比:0.4 理論値:6.67(mm)
11月13日課題†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.34118 | 2.35 | 君島 |
| 0.7 | 215780 | 0.33798 | 1.39 | 君島 |
| 0.8 | 159468 | 0.33563 | 0.69 | 高橋 |
| 0.9 | 90071 | 0.33203 | -0.39 | 高橋 |
| 1.0 | 61315 | 0.32997 | -1.2 | |
| 1.2 | 58111 | 0.329956 | -1.2 | 田村 |
| 1.4 | 47409 | 0.328156 | -1.5 | 田村 |
| 1.5 | 42068 | 0.325074 | -2.4 | 根本 |
| 1.8 | 24627 | 0.317161 | -4.8 | 根本 |
| 2 | 12228 | 0.3005115 | -6.9 | 藤原 |
| 4 | 5077 | 0.28405475 | -13.9 | 藤原 |
| 8 | 1795 | 0.23120033 | -30.6 | 森島 |
| 10 | 752 | 0.1612725 | -51.6 | 森島 |
ヤング率:7500(N/mm^2) ポアソン比:0.4 理論値:0.33334(mm)
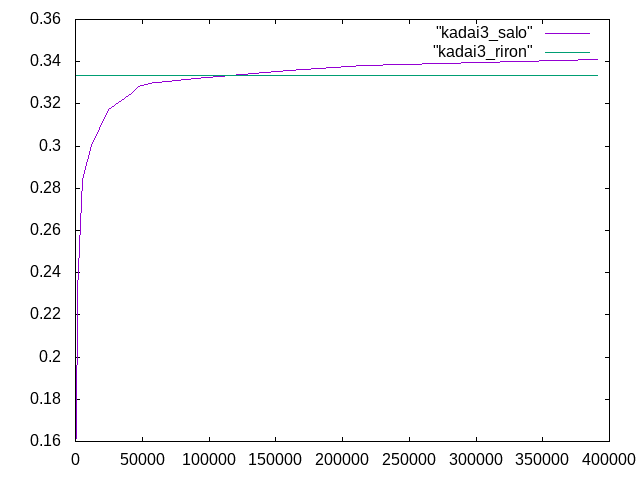
11月20日課題†
スパン100mm†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.440015 | 11.9 | 君島 |
| 0.7 | 215780 | 0.435823 | 10.8 | 君島 |
| 0.8 | 159468 | 0.4330131 | 10.1 | 高橋 |
| 0.9 | 90071 | 0.42766 | 8.72 | 高橋 |
| 1.0 | 61315 | 0.423881 | 7.77 | |
| 1.2 | 58111 | 0.423005 | 7.54 | 田村 |
| 1.4 | 47409 | 0.420309 | 6.86 | 田村 |
| 1.5 | 42068 | 0.418410 | 6.39 | 根本 |
| 1.8 | 24627 | 0.410464 | 4.36 | 根本 |
| 2 | 12228 | 0.396314 | 0.84 | 藤原 |
| 4 | 5077 | 0.378695 | -3.6 | 藤原 |
| 8 | 1795 | 0.342299 | -12.7 | 森島 |
| 10 | 752 | 0.298709 | -24.0 | 森島 |
ヤング率:7500(N/mm^2) ポアソン比:0.4 理論値:0.393334(mm)
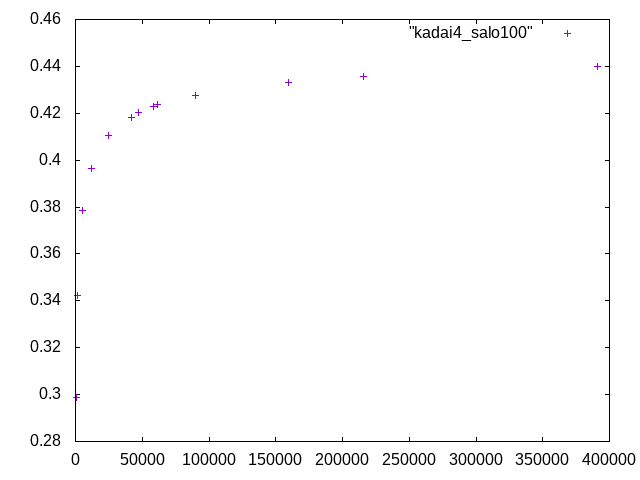
スパン50mm†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 251781 | 0.1253048 | 74.8 | 君島 |
| 0.7 | 109175 | 0.1172535 | 63.6 | 君島 |
| 0.8 | 75902 | 0.11527 | 60.8 | 高橋 |
| 0.9 | 71911 | 0.11413 | 59.3 | 高橋 |
| 1.0 | 47757 | 0.113602 | 58.5 | |
| 1.2 | 26945 | 0.108935 | 52.0 | 田村 |
| 1.4 | 22998 | 0.107298 | 49.7 | 田村 |
| 1.5 | 17689 | 0.103750 | 44.8 | 根本 |
| 1.8 | 14668 | 0.102133 | 42.5 | 根本 |
| 2 | 13986 | 0.069684 | -2.8 | 藤原 |
| 4 | 3009 | 0.0487895 | -32.0 | 藤原 |
| 8 | 967 | 0.0764429 | 7.2 | 森島 |
| 10 | 558 | 0.0768385 | 6.7 | 森島 |
ヤング率:7500(N/mm^2) ポアソン比:0.4 理論値:0.0716667(mm)
12月4日課題†
| メッシュサイズ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.8 | 226647 | 0.08053 | 56.9 | 高橋 |
| 0.9 | 127506 | 0.07678 | 49.7 | 高橋 |
| 1.0 | 92447 | 0.05276 | 2.79 | |
| 1.2 | 88386 | 0.05264 | 2.55 | 田村 |
| 1.4 | 78086 | 0.05261 | 2.49 | 田村 |
| 1.5 | 70032 | 0.072549 | 41.3 | 根本 |
| 1.8 | 34858 | 0.068375 | 33.2 | 根本 |
| 2 | 20313 | 0.063280 | 23.3 | 藤原 |
| 3 | 18229 | 0.0489236 | -4.68 | 君島 |
| 4 | 8067 | 0.050046 | -2.51 | 藤原 |
| 5 | 4846 | 0.036772667 | -28.3 | 君島 |
| 8 | 3814 | 0.0270877 | -47.2 | 森島 |
| 10 | 1716 | 0.0217906 | -57.5 | 森島 |
ヤング率(木材):7500(N/mm^2) ポアソン比(木材):0.4
ヤング率(鋼板):206000(N/mm^2) ポアソン比(鋼板):0.3
理論値:0.05133(mm)
春休みの課題†
幾何学非線形†
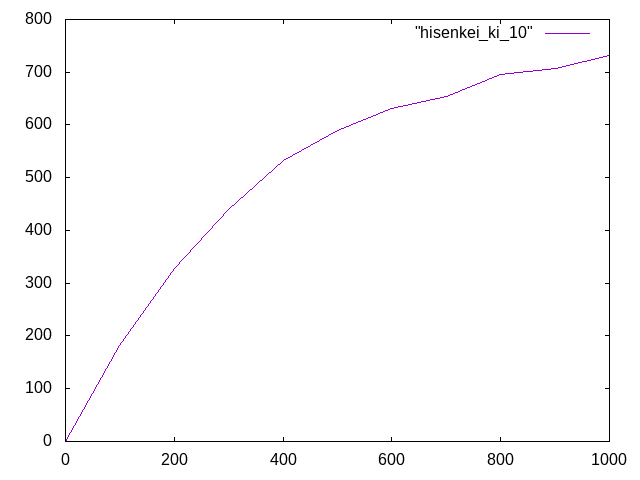
1000N†
鋼材を想定、荷重は1000N

300N†
荷重300Nのときは線形に近いグラフの形になった。

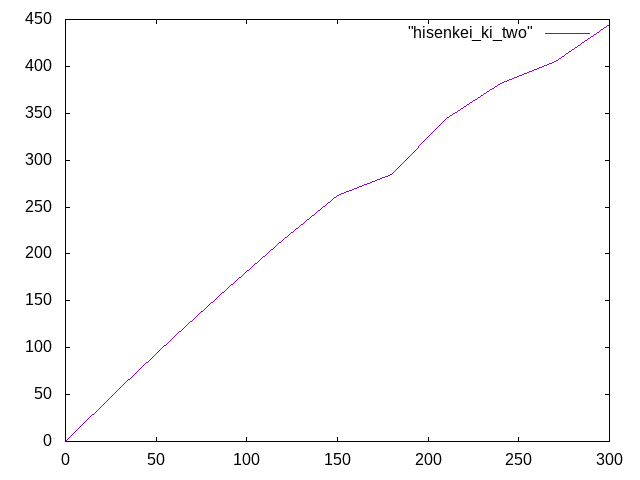
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
























