![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
結果はまだ出せていませんが、大まかなスライドの流れと疑問?を作りました。もしこれでだいたいの方向性がいいならテストが終わってからすぐにでも結果もスライドも作りたいです。
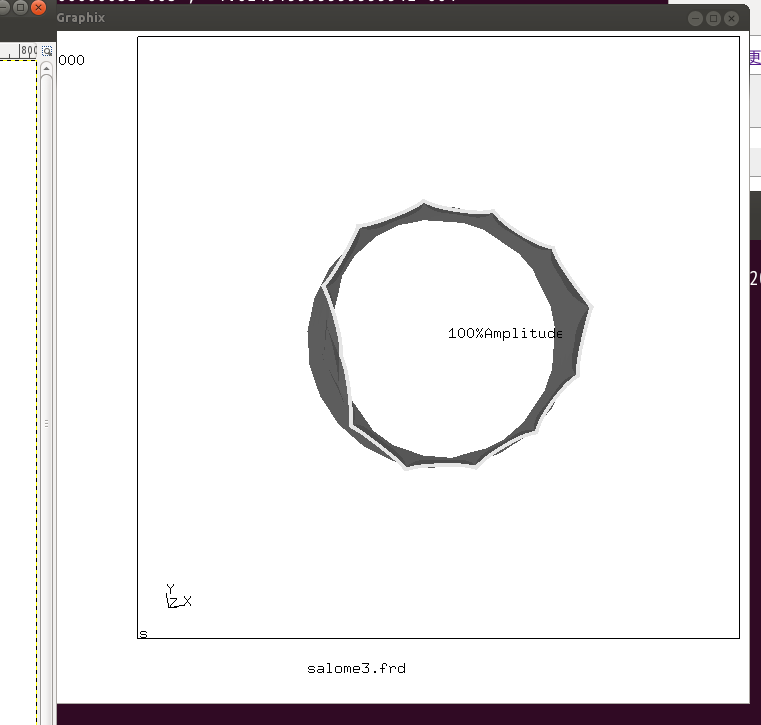

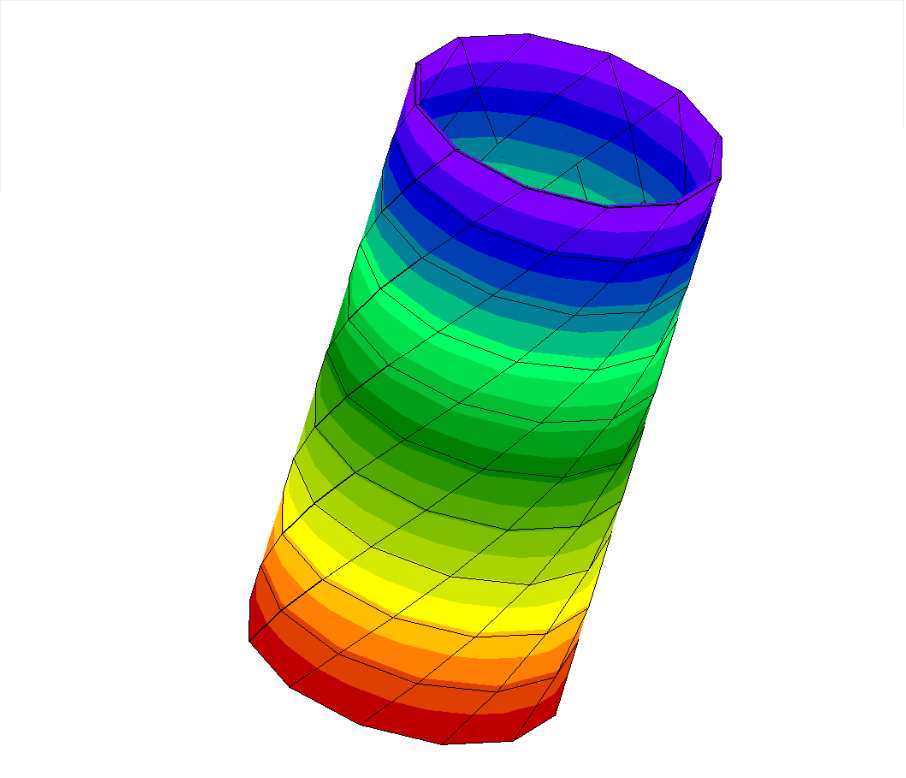
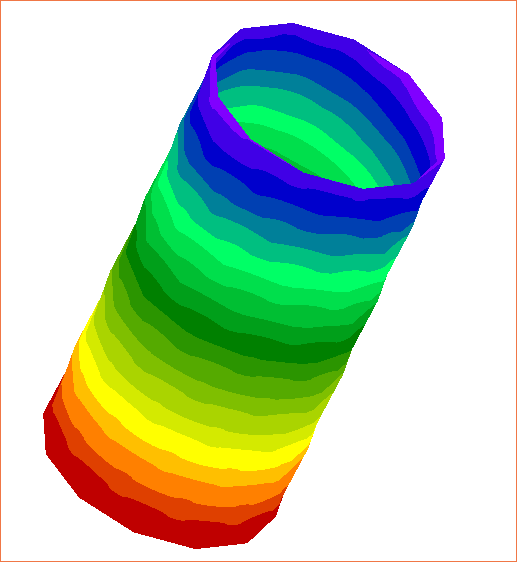

| 日付 | 時間帯 | 作業時間(hr) | 内容 | 立会 |
| 4/9 | 13:00~16:00 | 3 | タイピング練習 | |
| 4/13 | 14:30~16:30 | 2 | タイピング練習 | |
| 4/16 | 13:00~16:00 | 3 | 英文翻訳 | |
| 4/23 | 13:00~16:00 | 3 | 英文翻訳 | |
| 4/24 | 12:30~15:30 | 3 | パソコンゼミの課題 | |
| 4/27 | 14:30~17:30 | 3 | 卒論テーマ決定、草むしり | |
| 5/11 | 14:30~18:30 | 4 | sarome | |
| 5/18 | 14:30~18:30 | 4 | saromeでメッシュ分割 | |
| 5/21 | 13:00~15:00 | 2 | 英文翻訳 | |
| 5/25 | 14:30~18:00 | 3.5 | sarome | |
| 5/26 | 18:00~23:00 | 5 | sarome | |
| 5/27 | 17:00~23:00 | 6 | sarome | |
| 5/28 | 13:00~14:30 | 1.5 | 英文翻訳 | |
| 6/4 | 13:00~14:30 | 1.5 | 英文翻訳 | |
| 6/8 | 14:30~23:30 | 9 | 卒論 | |
| 6/11 | 13:00~14:30 | 1.5 | 英文翻訳 | |
| 6/15 | 14:30~16:00 | 1.5 | 状況報告と目標 | |
| 6/17 | 23:30~2:15 | 2.75 | 英語翻訳と課題 | |
| 6/18 | 13:00~21:15 | 8.25 | sarome課題 | |
| 6/19 | 13:00~17:00 | 4 | 一週間の目標の課題 | |
| 6/20 | 00:00~2:45 | 2.75 | 一週間の目標の課題 | |
| 6/22 | 14:30~16:30 | 2.0 | 状況報告と目標 | |
| 6/23 | 00:00~7:00 | 7 | 蛇腹折円筒 salome | |
| 6/25 | 13:00~14:30 | 1.5 | 英文翻訳 | |
| 7/2 | 13:00~14:30 | 1.5 | 英文翻訳 | |
| 8/3 | 3:00~8:00 | 5 | 卒論 | |
| 10/1 | 15:00~24:00 | 9 | 卒論 | |
| 10/2 | 12:00~24:00 | 12 | ダイヤカット円筒 グラフ | |
| 10/3 | 15:00~21:30 | 6.5 | ダイヤカット円筒 グラフ | |
| 10/4 | 00:00~5:00 | 5 | ダイヤカット円筒 グラフ | |
| 10/4 | 22:30~3:30 | 5 | ダイヤカット円筒 グラフ | |
| 10/6 | 14:00~20:00 | 6 | ダイヤカット円筒 グラフ | |
| 10/7 | 14:00~21:00 | 7 | ダイヤカット円筒 \( \TeX \) | |
| 10/8 | 13:00~21:00 | 8 | ダイヤカット円筒 \( \TeX \) | |
| 10/9 | 14:00~20:00 | 6 | ダイヤカット円筒 mesh | |
| 10/10 | 12:00~21:00 | 9 | ダイヤカット円筒 mesh | |
| 10/11 | 12:00~22:00 | 10 | ダイヤカット円筒 | |
| 10/13 | 14:30~19:00 | 4.5 | ダイヤカット円筒 | |
| 10/15 | 12:30~17:30 | 5 | ダイヤカット円筒 sarome | |
| 10/16 | 17:00~21:00 | 4 | ダイヤカット円筒 sarome | |
| 10/20 | 14:30~19:00 | 4.5 | ダイヤカット円筒 calculix | |
| 10/28 | 12:00~18:00 | 6 | ダイヤカット円筒 calculix | |
| 11/17 | 18:30~00:30 | 6 | ダイヤカット円筒 calculix | |
| 11/18 | 15:00~21:30 | 6 | ダイヤカット円筒 calculix | |
| 11/19 | 14:30~21:30 | 7 | ダイヤカット円筒 calculix | |
| 11/20 | 22:00~3:00 | 5 | ダイヤカット円筒 calculix | |
| 11/24 | 15:00~22:00 | 7 | ダイヤカット円筒 calculix | |
| 11/27 | 2:00~6:00 | 4 | ダイヤカット円筒 calculix | |
| 11/27 | 13:00~20:00 | 7 | ダイヤカット円筒 calculix | |
| 12/2 | 3:00~6:00 | 3 | ダイヤカット円筒 calculix | |
| 12/2 | 14:30~20:30 | 6 | ダイヤカット円筒 calculix | |
| 12/4 | 4:30~6:00 | 1.5 | ダイヤカット円筒 calculix | |
| 12/7 | 19:00~1:00 | 6 | ダイヤカット円筒 calculix | |
| 12/8 | 14:00~18:00 | 4 | ダイヤカット円筒 calculix | |
| 12/9 | 18:00~24:00 | 6 | ダイヤカット円筒 calculix | |
| 12/11 | 00:00~5:00 | 5 | ダイヤカット円筒 calculix | |
| 12/11 | 12:30~19:30 | 7 | ダイヤカット円筒 calculix | |
| 12/21 | 1:00~5:00 | 4 | ダイヤカット円筒 calculix | |
| 12/21 | 18:30~1:30 | 7 | ダイヤカット円筒 \( \TeX \) | |
| 12/22 | 2:30~8:00 | 5.5 | 発表準備 \( \TeX \) | |
| 1/12 | 18:30~1:30 | 7 | ダイヤカット円筒 | |
| 1/13 | 11:00~19:00 | 8 | ダイヤカット円筒 calculix | |
| 1/14 | 17:00~23:30 | 6.5 | ダイヤカット円筒 calculix | |
| 1/18 | 14:00~20:00 | 6 | ダイヤカット円筒 calculix | |
| 1/20 | 22:00~4:30 | 6.5 | ダイヤカット円筒 calculix | |
| 1/21 | 16:00~23:30 | 7.5 | ダイヤカット円筒 calculix | |
| 1/22 | 23:00~4:30 | 5.5 | ダイヤカット円筒 calculix \( \TeX \) | |
| 1/23 | 14:00~22:00 | 8 | ダイヤカット円筒 calculix \( \TeX \) | |
| 1/24 | 21:00~3:00 | 6 | \( \TeX \) | |
| 1/25 | 15:00~2:00 | 11 | 発表練習 スライド作り | |
| 1/26 | 15:00~1:00 | 10 | スライド作り | |
| 1/27 | 12:00~23:00 | 11 | スライド作り | |
| 1/28 | 15:00~3:00 | 12 | スライド作り | |
| 1/29 | 14:00~20:00 | 6 | 発表練習 | |
| 1/30 | 1:00~11:00 | 10 | calculix | |
| 1/31 | 20:00~6:00 | 10 | スライド作り |
| 合計 | 426.75 |
| 周方向 | |||||||
| 高さ方向 | 10 | 12 | 14 | 16 | 18 | 20 | |
| 10 | 3403560 | 3530762 | 3578586 | 3601138 | 3606268 | 3613957 | |
| 12 | 3309122 | 3481288 | 3538883 | 3565380 | 3570600 | 3579034 | |
| 14 | 3222636 | 3421143 | 3508587 | 3539009 | 3544340 | 3553534 | |
| 16 | 3079624 | 3373307 | 3484442 | 3518463 | 3523857 | 3533631 | |
| 18 | 2988599 | 3329172 | 3464703 | 3501891 | 3507111 | 3517473 | |
| 20 | 2902589 | 3288554 | 3448752 | 3488392 | 3493145 | 3503977 |
その後に
作業記録なので、これまでの経緯も削除しないで記録しておいていただけますか。