![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
論文タイトル、「螺旋折り円筒を用いた履歴型ダンパーの挙動」 研究題目、「螺旋折り円筒の構造物への適用性」 螺旋折りの自立、振動(免震・制震ダンパーほか)、補強、面のみ低剛性 圧縮展開、振動吸収、振動減衰、衝撃吸収、飛び移り座屈、機械分野、潰れる方向
圧縮と引張が逆、ダンパーの方の説明(写真とか)、図を十字にしてわかりやすく、履歴型ダンパーっていう。 伸縮履歴型ダンパーの説明だけで結構スペース使ってもいいかも。 salome使ったよって言う。
&link(ダンパーの役割と減衰特性,http://4menshin.net/report/b_vol7/vol7_1.html)
&link(地震動応答解析のおはなし,http://www.kozosoft.co.jp/gijyutu/s19.html)
&link(鉄筋コンクリート部材の動的荷重に対する復元力特性の影響,http://www.kochi-tech.ac.jp/library/ron/2009/2009infr/a1100418.pdf)
&link(折紙の数理と構造設計,http://www.cc.miyazaki-u.ac.jp/math/mpm/mpm2016/ab_ishida.pdf)、防振機能
螺旋折り円筒の中にバネ。
引張圧縮によって断面積が変わるのでそれに合わせて載荷と変位と時間の関係をうまい具合に調整した。 周期7.2秒で一辺1000mmの立方体±22mmの変位 上に浮いてるitaは、載荷量を見るためのもの。グラフの縦軸に1,000,000をかけると載荷量(N) グラフが綺麗だが振動に質量が付けばもっと違うグラフになりそう
&link(commファイル,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2018/endo/sindo/dyna.comm)
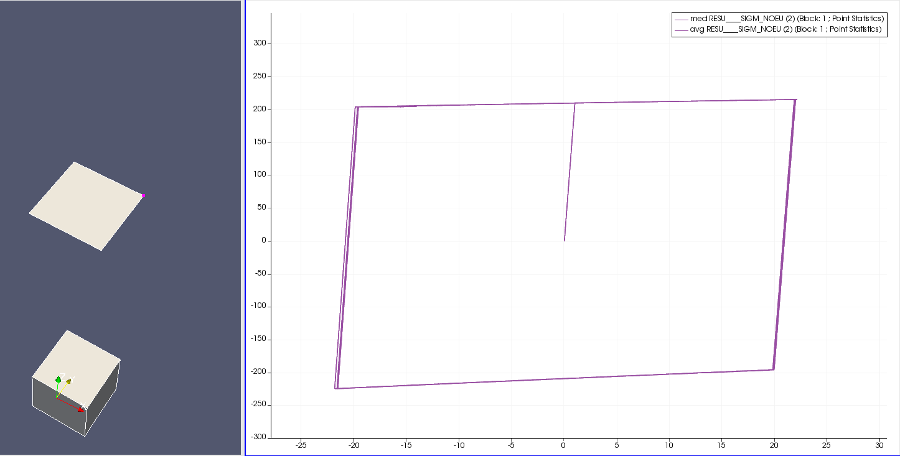
240MPaを6930ステップで与えたもの。ステップ数が少なくて誤差が振動に変わっておかしな数値が出た。 動的解析でこの境界条件だと、引張圧縮により面積が変わり応力が変わることで圧縮側のループが小さくなった。 解決法として圧縮力を大きく引張力を小さくする。
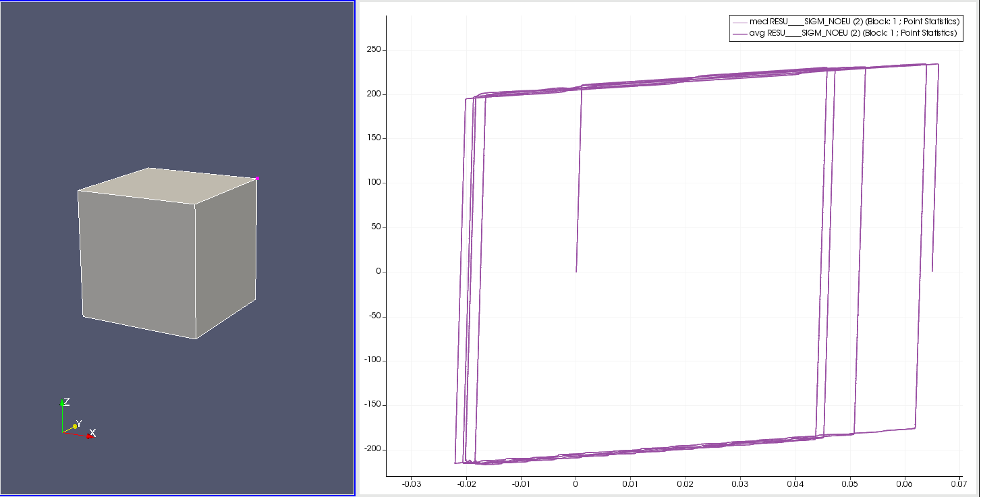
非線形動的解析のコマンドはDYNA_NON_LINEを使う。 例として降伏荷重210MPaの立方体でx=0、y=0、z=0面をそれぞれx、y、zとしてx、y、z方向に固定 z面の反対側の面をsaikaとして220MPa圧縮引張荷重を繰り返し与える。 下のcommファイルでは1000ステップを18回で18000ステップ4ループさせてる。 降伏後のステップ数が少ないと変な振動が出るが18000ステップは多すぎた、解析に半日かかる。 ただ、塑性後のタイムステップを粗くすると変な振動する。 コマンドDEFI_LIST_INSTを使わないと載荷の折り返しのところで計算が止まる。 詳しくはcommファイルのコメントアウトで
&link(dyna_non_lineのcommファイル,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2018/endo/sindo/dyna_test.comm)
振動解析のcommファイル。バネの伸縮。0Hzから1Hzまで0.01Hz刻みで解析。
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2018/endo/sindo/tes.comm
共振振動数付近の振動数を与えた時の最大変位。先端は10mm×10mmの面に1N/mm^で振動入力。 元の長さがバネ190mm質点10mm、すごく伸び縮みしてる。 もっと共振振動数に近づけたら最大変位は無限に増える(はず)。
静的解析してるから加速度を考慮して動的解析しないといけない? 振動解析に続く。
バウシンガー効果も考慮して、C=666.66667 C=0は完全弾塑性の時のみ。
salomeで、RELATION='VMIS_ECMI_TRAC'にすることで、幾何学非線形解析での降伏後の移動硬化の半径を指定できる。 DEFI_MATERIAUのPRAGERのCにより降伏曲面の中心値が決定する。計算式は、
&link(cpde-asterマニュアル,https://www.code-aster.org/V2/doc/v11/en/man_r/r5/r5.03.16.pdf)、 5 Identification of the characteristics of the material
※σ1σ2σ3は一方向の応力 「下のグラフの場合、」の式6×じゃなくて3×?
ヤング率4000降伏点40MPaの立方体を5%伸縮させてできた履歴曲線。 VMIS_ISOT_TRACでひずみ硬化が等方硬化則になってるので変な形状になってる。
DEFI_MATERIAUにPRAGER=_F(C=1000,),を追加、STAT_NON_LINE内でRELATION=VMIS_ECMI_TRACまた、DEFORMATION=PETIT_REACにすると、 drucker pragerの降伏曲面の中心値を決める値Cを変更できる。C=0だとvon misesの等方硬化則と同じになる。 下のグラフは伸縮を3%にした。
一応commファイル 立方体をx方向に引張圧縮繰り返し。 Group_2が固定面、Group_1が載荷面、Group_4とGroup_5はGroup_2内の隣り合う二辺。
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2018/endo/box.comm
力や変位の与えた量×(1,0,-1,0,1,0,-1,0)をそれぞれ10ステップづつで
INTERVALLE=(_F(JUSQU_A=1.0,
NOMBRE=10,),
_F(JUSQU_A=2,
NOMBRE=10,),
_F(JUSQU_A=3,
NOMBRE=10,),
_F(JUSQU_A=4,
NOMBRE=10,),
_F(JUSQU_A=5,
NOMBRE=10,),
_F(JUSQU_A=6,
NOMBRE=10,),
_F(JUSQU_A=7,
NOMBRE=10,),
_F(JUSQU_A=8,
NOMBRE=10,),),);fonc1=DEFI_FONCTION(
NOM_PARA='INST',
VALE=(0.0 ,0.0 ,
1.0 ,1 ,
2.0 ,0 ,
3.0 ,-1.0 ,
4.0 ,0 ,
5.0 ,1 ,
6.0 ,0 ,
7.0 ,-1.0 ,
8.0 ,0 ,),);
RESU=STAT_NON_LINE(MODELE=MODE,
CHAM_MATER=MATE,
EXCIT=_F(CHARGE=CHAR,
FONC_MULT=fonc1,),
COMPORTEMENT=_F(RELATION='VMIS_ISOT_TRAC', ←ELASだと弾性の大変形解析になる。
DEFORMATION='SIMO_MIEHE',), ELAS_HYPER使いたいけど何故かエラー。
INCREMENT=_F(LIST_INST=inst,),
NEWTON=_F(PREDICTION='TANGENTE',
MATRICE='TANGENTE',
REAC_ITER=1,),
CONVERGENCE=_F(RESI_GLOB_RELA=0.1,
ITER_GLOB_MAXI=200,),
ARCHIVAGE=_F(LIST_INST=inst,
CHAM_EXCLU='VARI_ELGA',),);
※DEFORMATIONは応力ひずみの計算の仕方(?)みたいなもの。
SIMO_MIEHE、PETIT_REAC(かなり細かい時間ステップが必要)、GDEF_LOG(未確認)、がいい。
GROT_GDEPは誤差ある。PETITは大変形できない。
※RELATIONは、降伏条件や硬化則を決めるもの。非線形解析できるものや大変形解析できるものとかある。
半径50mmの螺旋折り円筒の角の数と高さを変えて、バネ定数等を見る。 五角形螺旋折り円筒、高さが増えると圧縮時の最大応力も増える。
3角形高さ40mm螺旋折り円筒、縦軸 圧縮量(mm)、横軸 上辺のzz応力の平均値(N/mm2) だいたい合ってるけど数値全く違う
螺旋折り円筒の角を3-6、高さを10-80まで変えた時のバネ定数
elastica理論、先端に曲げモーメントを与えたとき片持ち梁の先端の縦変位から横変位を求める。 はじめに出る0は無視。
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2017/endo/fortran/elas/elas.f90
ヤング率は4000、棒の引張、横軸ひずみ縦軸応力(単位はN,mm,%)
ひずみが大きくなるとヤング率が増えていく。(対数ひずみ?)
約25%折りたたんだ時に応力が最大になる
蝶番をなくしたもの。折り目蝶番のモデルの最大応力が出るところで座屈してる? 最大応力(25%圧縮時)は10倍以上、降伏後は正しい解析不可。こっちは解析誤差が大きく解析できなかったのでメッシュを荒く切った。
折り目が蝶番普通の螺旋折り円筒
厚みのある螺旋折り円筒、5角形高さ70半径50厚さ0.1(単位はmmのつもり) meshはNETGEN1-2-3D モデル一個づつmesh作成後にcompound-mesh
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2017/endo/rasen_solid5_h70.comm
非線形解析では応力ひずみ関係を入力しないといけないが、正しい応力ひずみ関係を入力すると誤差が大きくなるので解析できなかった。(降伏後すごく固くしてた) RELATION='VMIS_ISOT_TRAC'からRELATION='ELAS'(線形弾性材料)にしたら解析できた。(たぶんバージョンが上がったからできるようになった) 今はDEFORMATION='GROT_GDEP'(内容不明)を使っているのでDEFORMATION='SIMO_MIEHE'(塑性変形の場合?)も試してみる。(DEFORMATIONだから変形関連?)
メモ RELATION='VMIS_ISOT_TRAC',(ミーゼスの降伏後線形の等方性の弾塑性モデルの値?) 紙、引張で2N/mm^2程で破壊(てきとうに測ったので全く正確ではない) 解析での螺旋折円筒の最大の、ミーゼス180MPa、z方向応力50MPaほど RELATION='ELAS_HYPER'(超弾性体)だとDEFORMATION='GROT_GDEP'のみ
参考
&link(SALOME Meca導入記:塑性,http://salome-meca.cocolog-nifty.com/blog/cat50907249/index.html)
辺でFuseするとヒンジになる。 メッシュを揃えるとCompound_Meshでもヒンジになる。
辺のメッシュを揃えたもの(Fuseせずにヒンジ化)
線でFuseすると勝手にヒンジになる。 ただ、シェル要素に使えない。
螺旋折の角数が増えるほど、半径に対する高さが小さくなるほど折りたたみやすくなる。
noとhiとroからkakuがわかる
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2017/endo/fortran/rasen.f90
折りたたむとき回転させる角度入り、これが大きいと折りたたみにくい。これから、高さが低いほど、角数が多いほど折りたたみやすいことが分かる
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2017/endo/fortran/rasen2.f90
salomeのcommファイル2016化 ver10からver12に aster、linear-static、data、~.commで右クリック、Run Eficas、translation一度ver11を経由してからver12にする。 ver10からver12に変換できないコードもあるので、エラーが出るところで修正
2016からpostproがなくなってParaVISのみになった。 ParaVISを開くとき、asterから直接行くと高確率でバグる。一度meshを経由すると良い。 Filters→common→Warp By Vectorで変形を見ることができる
elas_hyperつかえる New EntityのGenerationのThickness便利。立体要素で薄いモデル作るのが簡単に。
ふたつの同じ辺を共有したモデルのその辺でmeshが同じように切られてたらmeshをcompoundするだけでヒンジになる。meshをばらばらにすると辺の端だけヒンジになる。 ↑ならない?ばらばらになる?
metasequoiaで作ったモデルを保存(.mqo)blenderにインポート(遠藤の席のPCにプラグインがある、プラグイン入れないとインポート不可) 3Dプリンタ用データでエクスポート(.stl)Slic3rで開いていろいろ設定してSDカードにデータ入れて3Dプリンタにぶっさす。 metasequoia長さ100→slic3r(scale1000%)長さ1cm metasequoia長さ10→三層 プリント始める前にセンサー下げる 3Dプリンタ斜めになることあるからその時は手で直す、長いモデル作るときは気をつけてー
Z方向の変位など与えたい時の解析はMODELISATION='COQUE_3D'か'DKT' COQUE_3Dはひずみ小、変位大、回転大、DKTはひずみ小、変位小、回転小 シェル要素解析で大変形見れない、応力見れない、DDLの回転成分のせいか?(2016版になってから?前まで出来てたみたいだけど前も違う不具合あったぽい。) シェル要素での幾何学非線形解析はやめたほうがいい、回転成分消せればできるか?
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2017/endo/mennaiV10v11v12.comm
面内回転無理やりやったやつのcommファイル、
デスクトップの左上のアプリケーションのシステムツールからdconfエディターを起動 org→desktop→sessionでidle-delayの値を増やす。値は秒なので864000(10日)くらいにするといいかも デスクトップのシステムから設定のルック&フィールでスクリーンセイバーの設定からだと2時間までしか設定できない。
| コマンド | 効果 |
| convert -delay 10.5 gotai* gotai.gif | gotai1~の画像を10.5/100秒間隔でgif化 |
| convert rasen.gif -resize 840x480 rerasen.gif | rasenのサイズを840x480にしてrerasenで出力、.pngとかでもできる |
| unset key set /set yrange[0:40] reverse | タイトル消す/y軸を0-40の範囲で反転(gnuplot) |
| platex ○.tex→dvipdfmx ○.dvi | texのpdf化 |
| sed -i.txt -e "s/aaa/bbb/g" ○ | ○内の全てのaaaをbbbに置換、置換前の物は○.txtとして残る。 |
| awk '{a+=$28} END{print a;}' ○ | 28行目を合計して表示 |
| && | &&の前後のコマンドを一緒にやってくれる。 |
| コマンド | 効果 |
| set zeroaxis | これ以降xy軸がでてくる。 |
| set term png→set output 'our2'→plot 'ouhiz2' w l | グラフを画像出力 |
| plot 'text' using 1:($2*2) w l | 二行目を二倍、using 2:1でxy軸逆とかできる。 |
| set xtics 100 | x軸の1メモリが100になる。 |
| set datafile separator "○" | 区切りがスペースから○になる。 |
| unset key | 右上の消す。 |
| set size ratio 0.5 | 画面の縦横比を1:2にする |