藤田の卒論日誌

卒論日誌†

卒論進捗†

• 途中までのスライド
• &link(13740.pdf,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/13740.pdf)
• 今後の予定としては，まとめ作って，目次までいきたい

2/9†

• 1回目の発表練習
• とりあえず，言われたことを直す
• グラフ，絵の作り直し

CalculixでCLTモデル（弾塑性あり，荷重2000kN，引張圧縮強度1/6）†

• 圧縮比例限応力\( σ_{cp} = 38.3 (\mathrm{kgf/cm^2}) \)，圧縮強さ\( σ_{c} = 46.7 (\mathrm{kgf/cm^2}) \)，引張強度\( σ_{t} = 93.3 (\mathrm{kgf/cm^2}) \)

1層モデル†

• 実験は，おおよそ620kNで破壊（そのときの変位は，40.62mm）
• FEMでは，600kNで降伏（そのときの変位は，30.24mm）

8層モデル†

• 実験は，おおよそ620kNで破壊（そのときの変位は，40.62mm）
• FEMでは，540kNで降伏（そのときの変位は，36.46mm）

1層と8層の比較†

CalculixでCLTモデル（弾塑性あり，荷重2000kN，引張圧縮強度1/4）†

• 圧縮比例限応力\( σ_{cp} = 57.5 (\mathrm{kgf/cm^2}) \)，圧縮強さ\( σ_{c} = 70 (\mathrm{kgf/cm^2}) \)，引張強度\( σ_{t} = 140 (\mathrm{kgf/cm^2}) \)

1層モデル†

• 実験は，おおよそ620kNで破壊（そのときの変位は，40.62mm）
• FEMでは，800kNで降伏（そのときの変位は，32.60mm）

8層モデル†

• 実験は，おおよそ620kNで破壊（そのときの変位は，40.62mm）
• FEMでは，720kNで降伏（そのときの変位は，41.85mm）

1層と8層の比較†

CalculixでCLTモデル（弾塑性あり，荷重2000kN，引張圧縮強度1/2）†

• 圧縮比例限応力\( σ_{cp} = 115 (\mathrm{kgf/cm^2}) \)，圧縮強さ\( σ_{c} = 140 (\mathrm{kgf/cm^2}) \)，引張強度\( σ_{t} = 280 (\mathrm{kgf/cm^2}) \)

1層モデル†

• 実験は，おおよそ620kNで破壊（そのときの変位は，40.62mm）
• FEMでは，1160kNで降伏（そのときの変位は，33.80mm）

8層モデル†

• 実験は，おおよそ620kNで破壊（そのときの変位は，40.62mm）
• FEMでは，1000kNで降伏（そのときの変位は，40.74mm）

1層と8層の比較†

CalculixでCLTモデル（弾塑性あり，荷重2000kN）†

• 圧縮比例限応力\( σ_{cp} = 230 (\mathrm{kgf/cm^2}) \)，圧縮強さ\( σ_{c} = 280 (\mathrm{kgf/cm^2}) \)，引張強度\( σ_{t} = 560 (\mathrm{kgf/cm^2}) \)

1層と8層の比較†

• 1層では，1560kNで降伏（そのときの変位は，40.86mm）
• 8層では，1320kNで降伏（そのときの変位は，42.20mm）

実験と8層の比較†

• 実験は，おおよそ620kNで破壊（そのときの変位は，40.62mm）
• FEMでは，1320kNで降伏（そのときの変位は，42.20mm）

CalculixでCLTの8層モデル（弾塑性あり，荷重×2）（plcの設定ミスのため失敗）†

• 圧縮比例限応力\( σ_{cp} = 230 (\mathrm{kgf/cm^2}) \)，圧縮強さ\( σ_{c} = 280 (\mathrm{kgf/cm^2}) \)，引張強度\( σ_{t} = 560 (\mathrm{kgf/cm^2}) \)

1層モデル†

• &link(1so4.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/1so4.dat)
• 縦軸が荷重（kN），横軸が変位（mm）
• グラフ最後の点(40.8590,3120.00)で降伏しているっぽい．
• 3120.00(kN)で降伏．

8層モデル†

• 計算中(1/20/17)
• &link(8so4.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/8so4.dat)
• 縦軸が荷重（kN），横軸が変位（mm）
• グラフ最後の点(42.1962,2640.00)で降伏しているっぽい．
• 2640.00(kN)で降伏．

1層と8層の比較†

CalculixでCLTモデル（弾塑性あり，荷重1000kN，圧縮・引張強度JAS）†

• 圧縮強度\( \mathrm{F_c} = 19.2 (\mathrm{N/mm^2}) \)，引張強度\( \mathrm{F_t} = 14.4 (\mathrm{N/mm^2}) \)

1層モデル†

• &link(1so3.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/1so3.dat)
• 縦軸が荷重（kN），横軸が変位（mm）

8層モデル†

• &link(8so3.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/8so3.dat)
• 縦軸が荷重（kN），横軸が変位（mm）

1層と8層の比較†

CalculixでCLTの八層モデル作成（弾塑性あり）†

• 現在（2/18/2017）計算中
• 圧縮比例限応力\( σ_{cp} = 230 (\mathrm{kgf/cm^2}) \)，圧縮強さ\( σ_{c} = 280 (\mathrm{kgf/cm^2}) \)，引張強度\( σ_{t} = 560 (\mathrm{kgf/cm^2}) \)
• 計算結果はこんな感じ &link(clt8so.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/clt8so.dat)

計算結果†

• 縦軸が荷重（kN），変位（mm）

CalculixでCLTの一層モデル作成（弾塑性あり）†

• 圧縮比例限応力\( σ_{cp} = 230 (\mathrm{kgf/cm^2}) \)，圧縮強さ\( σ_{c} = 280 (\mathrm{kgf/cm^2}) \)，引張強度\( σ_{t} = 560 (\mathrm{kgf/cm^2}) \)
• 近藤さんの&link(clt1so.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/clt1so.f90)を計算してみた．ただし，計算に時間が掛かったので，出力ステップ数を50にしてみた&link(clt1so1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/clt1so.f90)．
• モデルの説明は，板の上半分に圧縮，下半分に引張を設定している．
• 計算してみた結果，降伏していない様子？弾塑性材料っぽくない．計算結果は以下の通り． &link(clt1so.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/clt1so.dat)

考えられる原因†

• まだ荷重が足りない？現在（2/18/2017）荷重を倍にして計算中&link(clt1so2.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/clt1so2.f90)

近藤より(17/01/18)†

• ひとまず&link(こんなの,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/plcltso.f90)とかで、計算結果をグラフにまとめてみては？

計算結果をグラフに(17/01/19)†

• 縦軸が荷重（kN），横軸が変位（mm）

CalculixでCLTの八層モデル（弾塑性なし）†

• 近藤さんの&link(clt8.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/clt8.f90)を計算してみた．
• 変位はこんな感じ&link(clt8.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/cle8.dat)
• 中央載荷面の変位平均（半面固定）：2.1308123111mm
• 実験値との相対誤差

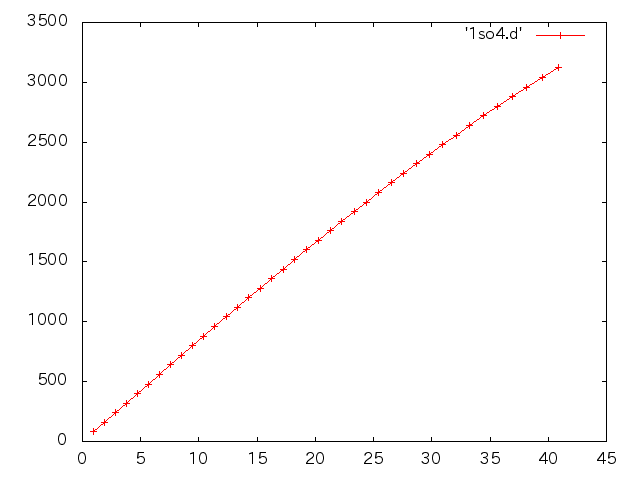
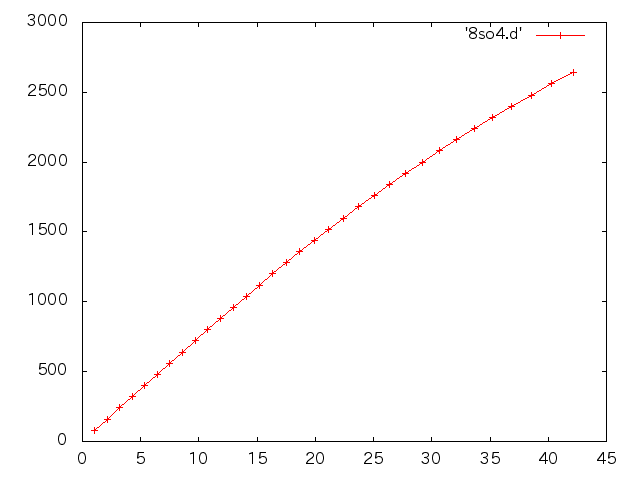
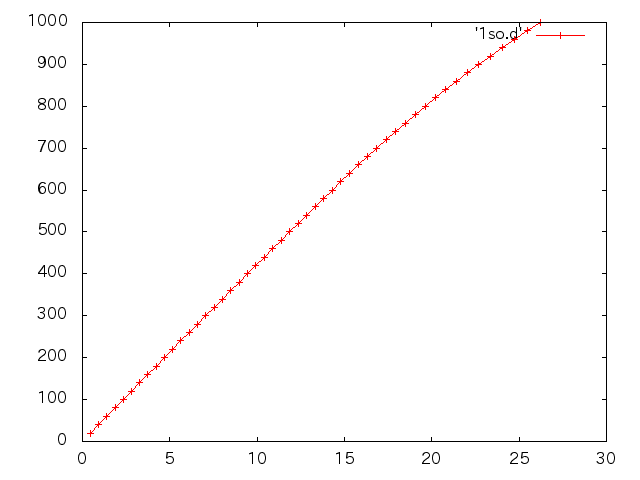
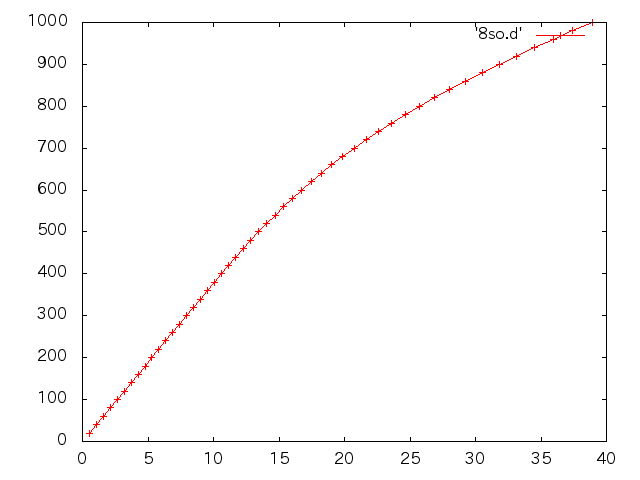
  試験前（%）	試験後（%）
  7.1	6.3

CalculixでCLTの一層モデル作成（弾塑性なし）†

• 近藤さんの &link(clt.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/clt.f90) を借りて作成してみた（といっても八層を一層にして，板の長さとか変えただけ）．
• こちら&link(ebn.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/ebn.f90)

• 実験での中央変位
  • 試験前：1.990
  • 試験後：2.005

• 条件などは以下の通り．海老名さんに揃えた．
  • CLTの寸法 　(X,Y,Z)=(2000,240,4000)[mm]
  • 1層モデル
  • 材料定数
    • \( E_z=3.5 \)GPa, \( E_x=1.7 \)GPa, \( E_y=0.2 \)GPa,
    • \( \nu_{xy}=\nu_{xz}=0.4\cdot\frac{\overline{E_{x}}}{\overline{E_{z}}}=0.4\cdot\frac{1.7}{3.5}\approx 0.194 \), \( \nu_{yx}=\nu_{yz}=0.4\cdot\frac{E_{y}}{\overline{E_{z}}}=0.4\cdot\frac{0.2}{3.5}\approx 0.0229 \), \( \nu_{zx}=\nu_{zy}=0.4 \),
    • \( G_{xy}=G_{yz}=G_{zx}=\frac{E_{z}}{15}=\frac{5}{15}\approx 0.33 \)GPa.
  • 載荷方法 500mm*200mmの面を板中央に作成し，100kNを載荷する．

• するとこんな感じになった．

• あとは海老名さんのモデル（salomeで作成中らしい）と比較してみるだけ．

近藤より(12/11)†

• &link(ebn.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/ebn.f90)は、ポアソン比・固定の位置や幅などが違うのでは?&link(clt.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/clt.f90)は佐々木さんの7層の梁を計算してみたくて作ったものなので、床版の計算をするためにはもっと色々と書き換えるところがあります。
  • ちなみに、変てこなポアソン比を与えると、計算はできてもstress-->misesとかがぶよぶよになるよ。
• 供試体2(海老名さんが今やっているもの)の計算には、&link(e1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/e1.f90)(1層)とか&link(e8.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/e8.f90)(8層)らへんをいじって使うのがよろしいかと。色々な境界条件をコメントアウトしてあるので、そこを海老名さんと合わせれば、ほとんどそのままで使えると思います。

変更点†

• 近藤さんの &link(e1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/e1.f90) を使って解いてみた結果，中央の載荷面の\( y \)方向変位の平均は，1.989579[mm]となった．
• 海老名さんとの違いは固定幅などが違うらしい．この辺もあわせていけば，salomeとの比較になる？
• ちなみに海老名モデルでは，変位は3[mm]程度とのこと？
• 変位はこんな感じ &link(e1.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/e1.dat)
• あと，海老名モデルの寸法が間違っている（板幅要確認）？実際は以下の通り．
  • CLTの寸法[mm] 　\( (x,y,z)=(4000,240,2010) \)[mm]

藤田の勘違い部分†

• \( z=2010 \)[mm]の部分はゴム板のはみ出し部分\( 5 \)[mm]\( ×2 \)を含んでいるため，板幅じたいは\( 2000 \)[mm]で計算する．
• その結果は，載荷面の\( y \)方向変位の平均は，2.141908[mm]となることがわかった．
• ちなみにdatファイル &link(e1-1.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/e11.dat)
• あと変更したファイル &link(e1-1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/e11.f90)

考察†

• \( 0.3 \)[mm]程度の誤差が出た．無視していいのか…
• 考えられる原因は，salome（以下sal）がゴム板とCalculix（以下cal）H鋼になっている点．
• 変位の読み方，salは最大変位，calは載荷面での平均変位．
  • 余談だが，calで最大変位を読むと，\( 2.32 \)[mm]と更に誤差が大きくなる．
• 誤差はこんな感じ？

\( \dfrac{\mathrm{cal-sal}}{\mathrm{sal}}×100 = 18.7 \% \)

\( \dfrac{\mathrm{cal-sal}}{\mathrm{cal}}×100 = 15.8 \% \)

近藤より(12/14)†

• &link(e1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/e1.f90)の"!#--境界条件の節点群"以下に、境界条件を入れる節点群について書かれているところがありますが、そこも海老名さんに合わせる必要があります。今、&link(e1-1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/e11.f90)が半面固定になっているけれど、海老名さんに合わせるのなら全面固定というように。
• それから、あまり良くない手法ですが、楽なので&link(e1.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/e1.f90)では、節点群を座標指定で集めています。つまり、要素分割によっては意図する場所ぴったりに境界条件を入れられません。具体的には、
  • 2000mmを50分割すると1要素あたりの長さは40mmになるので、40mmの倍数でしか節点群を指定できません。
  • つまり、端から135mmの場所を固定したい場合でも、端から120mmの場所しか固定しないことになります。
• これをすぐに解消するには、要素分割を細かくすることです。例えば2000mmを100分割すれば、端から140mmのところで固定できるので、少し近づきます。
• プログラムをところどころ書き換えればぴったりの位置に節点を持ってくることもできるので、ぴったりじゃないと気持ち悪いというのであれば、近藤に言って下さい。
  • あと、海老名さんのも4面体の1次要素で計算しているけど、それだと変形が小さくなりがちだよね。

変更点†

• 半面固定から全面固定にしてみた．あと，板幅の分割数を100にしてみた． &link(e1-2.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/e12.f90)
• これで，固定の場所が端から140mmの位置になる（海老名モデルでは135mm）．
• 結果，中央載荷面の平均の変位は，2.052015mmとなった． &link(e1-2.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/e12.dat)
• 誤差はこんな感じ？

\( \dfrac{\mathrm{cal-sal}}{\mathrm{sal}}×100 = 13.7 \% \)

\( \dfrac{\mathrm{cal-sal}}{\mathrm{cal}}×100 = 12.1 \% \)

8層モデルだと†

• 中央載荷面の変位平均（半面固定）：2.037768mm &link(e8h.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/e8.dat)

• 中央載荷面の変位平均（全面固定）：2.281082mm &link(e8z.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/ez8.dat)

• 海老名さんモデルとの比較をすると，こんな感じ

考察†

• 8層にするとsalomeとの誤差が大きくなる．
• 概要 &link(kouki.tex,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/kouki.tex) &link(model,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/model.eps) &link(fg,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/fg.eps)

近藤より(12/17)†

　&link(kouki.tex,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/kouki.tex)、見ました。海老名君とseiteki4mx2m.xlsxを確認してみたけど、荷重centerの変位計7が1.990mm,2.005mmになっているのは、(sheet比較の下の方の表とグラフによると)20～30秒(交番載荷前)のときと20～35秒(交番載荷後)のときの変位なので、荷重が大体、8.2\( \times \)9.8\( \approx \)80kNのときのもだと思われます。しかし、藤田君と海老名君は、確か荷重の最大値(9.87\( \times \)9.8\( \approx \)96.7kNから9.58\( \times \)9.8\( \approx \)93.9kN .あるいは100kN?)を与えてFEMで計算していたと思うので、実験値との誤差を求めるときにどちらかに合わせる必要があるのでは? 多分、CCX8層が実験値に一番近くなると思うよ。

藤田の勘違い（12/18）†

• なるほど，こちらの解析では最大荷重で計算しています．実験結果の見る部分を間違えていました．

• FEM解析では弾性材として解いているので，フックの法則に従っていると考えます．なので，変位は荷重に比例すると考えて，FEMで解いた結果に \( \dfrac{80}{9.73 \times 9.8} \) をかければ，\( 80 \)kNでの結果になると考えているんですが，どうでしょうか？

• FEMは線形計算だから、それがいいね。(近藤12/18)

ちなみに8層モデルをボルト線状で線拘束すると†

• &link(e8s.dat,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/es8.dat)
• &link(e8s.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/es8.f90)

• 実験値との相対誤差は

12月18日の勘違いから†

荷重が大体，\( 80 \)kNのとき中央変位が，1.990mm，2.005mmになっているから，salomeには0.8を，Calculixには\( \dfrac{80}{9.73 \times 9.8} \)をかけて見る．

1層モデルを修正してみると．†

8層モデルを修正してみると．†

後期†

12月9日からの†

• salomeで解いたモデルと，calculixで解いたモデルの比較をする．
• それに弾塑性を入れてみる．
  • まずは一層モデルで，板厚半分から上を圧縮の降伏強度を，下を引張の降伏強度を設定して解く（降伏点は1方向）．
  • 荷重は徐々に増えていく感じの荷重を掛ける．
• それを八層モデルにしてみる．
  • 一層毎に降伏強度の設定（降伏点は2方向）．
• 最終的に一層と八層の比較など出来れば良いのでは．

12月2日からの†

• CalculiXで弾塑性をやることをすすめる．
• 現状，gfortranでなんかして，cgxをターミナルでやるとモデルとかが表示される．
• みたいなところまで．
• 変位とか視覚的に見れるし，見方はなんとなくわかってきた．
• あとは，弾塑性でCLTの降伏を表現するところが最終目標．
• まずは梁に載荷するとか，単純なことから進めていきたい．

11月18日からの†

• 中央断面の応力分布を作りたい．降伏を見たいから．
  • 現状ではsalomeで応力を計算できていない．そのため作れない．
  • SIGM_NOEUがどうやっても出てこない．

11月13日†

• とりあえず2材料で作成．材料定数とかは適当．

• 黒で囲んだAの部分（bou2）とその他の部分（bou1）で複合材として解いてみた．どちらも弾性としてはいける．

• Aを弾塑性にしてみると，以下のエラーがでる．意味は「ECRO_LINEが見つからない」だそう．

• (

    ! <S> Exception utilisateur levee mais pas interceptee. !
    ! Les bases sont fermees.                               !
    ! Type de l'exception : error                           !
    !                                                       !
    !  comportement :ECRO_LINE non trouv&#233;   

• )

• とりあえず，commファイル &link(弾性,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/kari.comm)，&link(弾塑性,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/danmo.comm)

今後のこととか†

• salomeでの弾塑性ができることがわかったので（現在のバージョンでも，ただし計算すると保存できなくなることがしばしばあるが），フィンガージョイントの再現をしてみる．
• 問題は，割と小さい荷重でないとうまくいかないということ．フィンガージョイントの強度も調べてあるが，そのままでやるとおそらく爆発してしまう．
• つまりスケール（物のサイズだけ小さくするのではなく，荷重自体小さくする）を小さくしても，問題ないように解かないといけない．
• とりあえずモデル作ってから考えよう．

11月12日†

• 弾塑性ができたようだ．しかし，荷重とか極端な値でないとできないようだ．
• 現時点で，salomeで弾塑性が引っ張りと曲げどちらでもできることがわかった．
• 出来なかった原因としては，分割数が少なかったこと？
• 主な変更点
  • 分割数を20から100に変更
  • commファイルの変更点
  • ( RESU=STAT_NON_LINE(MODELE=MODE,

                      CHAM_MATER=MATE,
                      EXCIT=(_F(CHARGE=CHAR,),
                             _F(CHARGE=loadP,
                                FONC_MULT=ramp,),),
                      COMP_INCR=_F(RELATION='VMIS_ISOT_LINE',
                                   TOUT='OUI',),
                      INCREMENT=_F(LIST_INST=inst,),
                      METHODE='IMPL_EX',
                      CONVERGENCE=_F(RESI_GLOB_RELA=1e-6,
                                     ITER_GLOB_MAXI=10,),
                      ARCHIVAGE=_F(LIST_INST=inst,
                                   CHAM_EXCLU='VARI_ELGA',),);

  • )

から

• ( RESU=STAT_NON_LINE(MODELE=MODE,

                    CHAM_MATER=MATE,
                    EXCIT=(_F(CHARGE=CHAR,),
                           _F(CHARGE=loadP,
                              FONC_MULT=ramp,),),
                    COMP_INCR=_F(RELATION='VMIS_ISOT_LINE',
                                 DEFORMATION='PETIT',
                                 TOUT='OUI',),
                    INCREMENT=_F(LIST_INST=inst,),
                    METHODE='NEWTON',
                    NEWTON=_F(REAC_ITER=1,),
                    CONVERGENCE=_F(RESI_GLOB_RELA=1e-6,
                                   ITER_GLOB_MAXI=10,),
                    ARCHIVAGE=_F(LIST_INST=inst,
                                 CHAM_EXCLU='VARI_ELGA',),); 

• )

に変更

• commファイルはこちら　&link(danso1_2.comm,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/danso1_2.comm)

11月11日†

• salomeで弾塑性をできるようにする．
• http://www.str.ce.akita-u.ac.jp/cgi-bin/gwiki/wiki.cgi?Salome%a5%e1%a5%e2#i70 をsalomeで実行すると，計算後salomeがフリーズしてしまう．結果できない．計算量が多いのか，計算自体は完成しているので，その辺をどうするか．→放置しておけば問題はない．
• 自分で作ったモデルだとヤング率と荷重変えただけで計算ができなくなる．

現状のエラーとcommファイル†

<S> Exception utilisateur levee mais pas interceptee.                 !
  ! Les bases sont fermees.                                               !
  ! Type de l'exception : NonConvergenceError                             !
  !                                                                       !
  !    Arret : absence de convergence avec le nombre d'it&#233;rations requis. 

以下訳

S>ユーザー例外なく、堤防のため停止していません。！

  ！塩基が閉じられています。！
  ！例外の種類：NonConvergenceError！
  ！！
  ！停止：繰り返しの必要な数と収束の欠如を。

&link(danso1_1.comm,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/danso1_1.comm)

11月4日†

• salome（ver.2013，STR10）で弾塑性を解こうとすると，うまくいかないので以下の案

案1†

• CalculiX導入案

案2†

• salomeのver.違い導入案

ここまでの†

• フィンガージョイントを再現するため，弾塑性をsalomeで解こうとする．
• いまのところうまくいっていない．
• CLTのモデル化も進めていく方が良さそう．
• 11月はCLTの方がメインになるか，しかし以前の簡易モデルで実験値と近い値は出ていたので，あまり急ぐ必要もないか．

10月31日†

• salomeで弾塑性してみたが，どんな値（荷重を変えた，面載荷を線載荷にしてみた）を入れても同じ結果が出ているので，なにか間違っているらしい．

10月23日†

• 弾塑性してみた．結果が出力されない．途中経過． (&link(danso.comm,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/danso.comm))
  • ( RESU=CALC_NO(reuse =RESU,

                RESULTAT=RESU,
                OPTION=('SIGM_NOEU','SIEQ_NOEU',),);

  • )

を消すとPost-ProにFieldsが出てくるけど，RESU_DEPLしか出てこない．消したり増やしたりでなにか出来ないか考える．

10月21日†

• とりあえず単純梁全体を弾塑性でsalomeで解いてみる．正しいか確認をする．三角形分布とか考える．

10月14日†

案1†

• フィンガージョイント部分とその他の部分（その他の部分の方が降伏しにくい）で降伏点の違う弾塑性で解く．
• 荷重を掛けて降伏したらその部分がなくなる感じになるので，破壊しなくてもフィンガージョイントから破壊が進行するのを見ることができるのでは…

案2†

• フィンガージョイント部分を弾塑性で，その他の部分を異方性材料で解く．
• 板を重ねたときにフィンガージョイント部分の上の板の部分に降伏点を設ける．

10月11日†

• 2材料で再現してみた．破壊させてないからなんともいえない．
• まだ弾塑性材とかにはしていないので，今週中にモデルを作成してみる．

10月7日†

• フィンガージョイントをプラスチック的な素材で再現してみる案
• それで降伏点を作って，破壊してみる．

10月5日†

• 簡易モデルに亀裂の設定をしてみた．Asterの計算は出来ているが，PostProに現れない．今後の課題．

10月3日†

亀裂の設定†

• 梁の破壊を考えるときに，亀裂を設定してできないかと考えた．
• もちろん，塑性もできるが，木材だし亀裂から試してみた．
• ちなみに，こちらのページを参照． https://sites.google.com/site/codeastersalomemeca/home/salome-meca-chutoriaru6/geometry-meshmojuru6-2013

夏の課題†

9月25日後期†

• 中央変位．横軸が時間，縦軸が変位．

• 繰り返し荷重っぽくしてみた．横軸が時間，縦軸が変位．データでみるとそれっぽい（平面での変位）．

9月25日中期†

• 0秒から1秒で10分割して，荷重を0割→1割→0割…みたいな感じで繰り返し荷重を掛けることができた．
• もちろん，現状では破壊とか疲労とかの設定をしていない．

9月25日前期†

• 9月24日のグラフは横軸が周波数(Hz)，縦軸が変位の割合（無次元数）？だったっぽい．
• なのでcode-asterを少し修正

修正前

• ( IMPR_RESU(MODELE=MODE,

           FORMAT='MED',
           RESU=_F(MAILLAGE=MAIL,
                   RESULTAT=MODES,
                   NOM_CHAM='DEPL',),);

IMPR_RESU(MODELE=MODE,

         RESU=_F(RESULTAT=dynaTR,
                 NOM_CHAM='DEPL',
                 NOEUD='N3',),);

• )

修正後

• ( IMPR_RESU(MODELE=MODE,

           FORMAT='MED',
           RESU=_F(MAILLAGE=MAIL,
                   RESULTAT=dynaTR,
                   NOM_CHAM='DEPL',),);

• )

• 計算の出力が2個？だったのを，1個にしてみた．
• code-asterの中身は以前と変わらず．

• 修正の結果，時間と変位の関係を出力することに成功した．

今後の課題†

• 現状だと0秒から1秒まで段階的に荷重を10割まで掛けるみたいになってしまっている．
• 繰り返し荷重をその設定からうまく設定していく．

9月24日ごろ†

• よく考えたら23日のグラフは時間-応力グラフで意味がなさそう．
• 少し修正して時間-変位グラフにしてみた．
• 縦軸が変位，横軸が時間

• たぶんなっているのだろうけど，数値がどう見てもおかしい（変位1ってなんだ）．
• ただし，振動しながら0に収束しそう（載荷回数5回）なので，実験でのグラフにはだいぶ近づいている．
• 正しいかチェックしていく．

9月23日ごろ†

• ParaVisでいろいろいじってみてこんなグラフに（たぶん下の緑の線）．

• それっぽいが，正しいのかよくわからない．

9月12日ごろの話†

• 変動負荷のcode-asterの書き換えはできた．しかし，1回の積載で計算に数分かかる．問題は20万回積載しなければいけない．あと負荷も変化させていかないといけない．
• 5回の積載までできた．これが正しく出来ているかこれから評価していく．
  • 等方性材料として
  • ヤング率（実験値）：\( E=5.65 \)GPa
  • ポアソン比（杉ぐらい）：\( \nu = 0.4 \)
  • \( \alpha 粘性減衰 \)：0.00001
  • 密度：\( \rho = 424 \mathrm{kg/mm^3} \)
• CLTやってて感じることは，解析だけだと集成材でいいんじゃないかって思ってしまう．今のデータのまま発表したら「集成材でいいんじゃないの？」って質問でつんでしまうな．CLTだから出来るところも研究から見つけないとな．

今後の課題とか†

• 粘性減衰を設定しないといけない（らしい）んだけど，何に影響しているのかいまいち．少し調べる．
• 積載回数が20万回，つまりcode-asterで入力すべき項目が80万回あるわけだから手では不可能．入力できても計算できないのでは．少し工夫して計算したい．
• 県立大のモデルだからある程度単純だが，山口大のモデルになると車輪2つ，かつ載荷回数80万回になるわけで，複雑になるし，とりあえず単純なモデルで出来ているのか確認したい．夏の課題からは切り捨てる．
• 計算の準備は出来ているので，異方性でもモデル作成したい．しかし，県立大モデルはそれぞれのヤング率出してないしな．とりあえず，杉材のヤング率で異方性の計算してみるか．
• 今はアニメーションで出力しているんだけど，データとして出力，グラフ化したい．

9月11日ごろの話†

• 等方性材料でも誤差があまりでなかったが（曲げ試験だから），等方性と異方性でどう変わるかモデルの作成をする（予定）．
• 山口大のモデルも作成したいが，実験のデータがないので解析しても比較対象がない．
• 繰り返し荷重は，corde-asterの変動負荷で試してみようと思う．時間で荷重を変えられるらしいので，車輪が行ったり来たりできるか試してみよう（予定）．
• 変動負荷のcode-asterの書き換えがうまくいかず．もう少し試行錯誤してみる．

9月10日ごろの話†

• とりあえず県立大学のモデル作成（ヤング率は実験値使用，等方性材料として計算）
  • ヤング率=5.65GPa
  • ポアソン比=0.4
• 上実験値，下計算

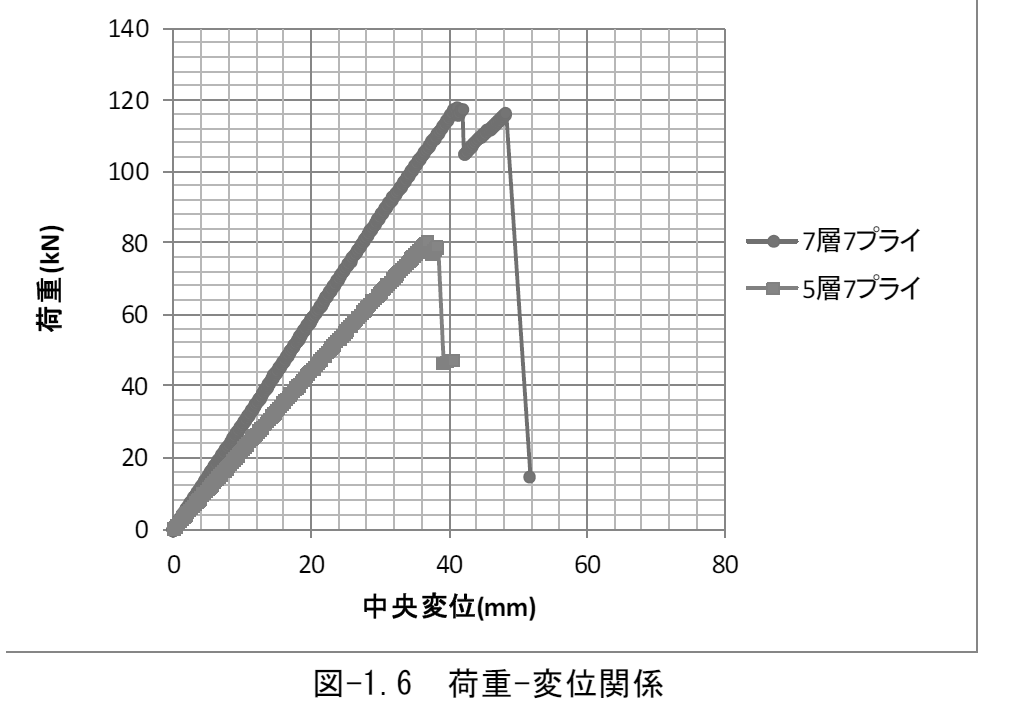（引用：佐々木貴信ほか:橋梁用床版用途としてのCLTの性能評価）

• 意外と誤差は少ないよう．まあヤング率を実験から求めて，解析ではそのヤング率使っているので，実験ありきの解析のような気がする．だらか，あんまり意味のあることではないと思う．
• もちろん，実験では118.8kNで破壊しているが，解析では破壊せず荷重がかかり続ける．この辺も考えていきたいな．

8月22日～8月28日までの予定†

• 先週の内容を引き続き
• 先週は詰め込みすぎたので，とりあえず基本的なモデルの作成から行う．
• 床版への利用なので，輪荷重とかそのへんの構造力学の復習も行う．

8月15日～8月21日†

うまくいっていないので，とりあえず次週にもちこし．

8月15日～8月21日までの予定†

• CRTモデルの作成（拘束部分に線荷重，縦方向と横方向のヤング率は平均値）
• 板の層ごとにヤング率の設定（たぶん等方性で）
• できれば異方性の設定なんかも

8月8日～8月14日†

特に進展なし

memo†

CalculiXの起動から（ターミナルで）†

• fortranのファイルを作るor入手する．
  • ( gfortran aaa.f90 -o aaa
  • )
• コンパイルしたaaaをinpファイルにする．
  • ( ./aaa>aaa.inp
  • )
• なんかccx
  • ( ccx aaa
  • )
• あとはcgx
  • ( cgx aaa.frd
  • ) とか
  • ( cgx -c aaa.inp
  • ) とか
• たぶんこんな感じで使える．

繰り返し荷重（変動負荷）†

• 調べてもあまり出てこないから一応メモしておく．
• 変動負荷で繰り返し荷重できるなって思ったので，他にやり方あるかもしれない．
• 一応，code-aster

• ( DEBUT();

MA=DEFI_MATERIAU(ELAS=_F(E=5650000000.0,

                        NU=0.4,
                        RHO=4.24e-10,
                        AMOR_ALPHA=0.00001,),);   #''粘性減衰''

MAIL=LIRE_MAILLAGE(FORMAT='MED',);

#MAIL=MODI_MAILLAGE(reuse=MAIL,

#                  MAILLAGE=MAIL,
 #                 ORIE_PEAU_3D=_F(GROUP_MA=('load',),),
  #                );

MODE=AFFE_MODELE(MAILLAGE=MAIL,

                AFFE=_F(TOUT='OUI',
                        PHENOMENE='MECANIQUE',
                        MODELISATION='3D',),);

MATE=AFFE_MATERIAU(MAILLAGE=MAIL,

                  AFFE=_F(TOUT='OUI',
                          MATER=MA,),);

CHAR=AFFE_CHAR_MECA(MODELE=MODE,

                   DDL_IMPO=(
                       _F(GROUP_MA='hidari',
                          DX=0.0,
                          DY=0.0,
                          DZ=0.0,),
                       _F(GROUP_MA='migi',
                          DX=0.0,
                          DY=0.0,),
                       ),
                   FORCE_FACE=(
                       _F(GROUP_MA='load',
                          FX=4000000.0,),
                       ),
                   );

MACRO_MATR_ASSE(MODELE=MODE,

               CHAM_MATER=MATE,
               CHARGE=CHAR,
               NUME_DDL=CO('NUMEDDL'),
               MATR_ASSE=(_F(MATRICE=CO('RIGIDITE'),
                             OPTION='RIGI_MECA',),
                          _F(MATRICE=CO('MASSE'),
                             OPTION='MASS_MECA',),
                          _F(MATRICE=CO('amore'),
                             OPTION='AMOR_MECA',),),);

loadV=DEFI_FONCTION(NOM_PARA='INST',VALE=(0,1, #(時間,荷重

                    0.025,1,                         #''荷重の1は設定した荷重の1倍の意味''
                    0.0251,0,
                    0.05,0,
                    0.051,1,
                    0.1,1,
                    0.101,0,
                    0.15,0,
                    0.151,1,
                    0.2,1,
                    0.201,0,
                    0.25,0,
                    0.251,1,
                    0.3,1,
                    0.301,0,
                    0.35,0,
                    0.351,1,
                    0.4,1,

0.401,0,

                         ),);

stepTR=DEFI_LIST_REEL(DEBUT=0.0,

                     INTERVALLE=_F(JUSQU_A=0.4,      #''JUSQU_A= その時間まで計算''
                                   PAS=0.0001,),);   #''PAS= 時間間隔，これだと0.0001間隔で時間進む''

MODES=MODE_ITER_SIMULT(MATR_A=RIGIDITE,

                      MATR_B=MASSE,
                      CALC_FREQ=_F(OPTION='PLUS_PETITE',
                                   NMAX_FREQ=10,),);    #''結果の数''

dynaTR=DYNA_LINE_TRAN(MODELE=MODE,

                     CHAM_MATER=MATE,
                     MATR_MASS=MASSE,
                     MATR_RIGI=RIGIDITE,
                     MATR_AMOR=amore,
                     NEWMARK=_F(DELTA=0.5,),
                     EXCIT=_F(CHARGE=CHAR,
                              FONC_MULT=loadV,),
                     INCREMENT=_F(LIST_INST=stepTR,),);

IMPR_RESU(MODELE=MODE,

         FORMAT='MED',
         RESU=_F(MAILLAGE=MAIL,
                 RESULTAT=MODES,
                 NOM_CHAM='DEPL',),);

IMPR_RESU(MODELE=MODE,

         RESU=_F(RESULTAT=dynaTR,
                 NOM_CHAM='DEPL',
                 NOEUD='N3',),);

FIN();

• )

修正前

• ( IMPR_RESU(MODELE=MODE,

           FORMAT='MED',
           RESU=_F(MAILLAGE=MAIL,
                   RESULTAT=MODES,
                   NOM_CHAM='DEPL',),);

IMPR_RESU(MODELE=MODE,

         RESU=_F(RESULTAT=dynaTR,
                 NOM_CHAM='DEPL',
                 NOEUD='N3',),);

• )

修正後

• ( IMPR_RESU(MODELE=MODE,

           FORMAT='MED',
           RESU=_F(MAILLAGE=MAIL,
                   RESULTAT=dynaTR,
                   NOM_CHAM='DEPL',),);

• )

2つの材料で解く†

• salomeでモデル作成，材料毎にGroupを作る．
• コマンドファイルを以下のように変更．

• ( MA=DEFI_MATERIAU(ELAS=_F(E=xxx,

                          NU=xxx,),);

• )

から

• ( MA1=DEFI_MATERIAU(ELAS=_F(E=xxx,

                          NU=xxx,),);

MA2=DEFI_MATERIAU(ELAS=_F(E=△△△,

                        NU=△△△,),);

• )

さらに

• ( MATE=AFFE_MATERIAU(MAILLAGE=MAIL,

                    AFFE=_F(TOUT='OUI',
                            MATER=MA,),);

• )

から

• ( MATE=AFFE_MATERIAU(MAILLAGE=MAIL,

                    AFFE=(_F(GROUP_MA='Group1',
                             MATER=MA1,),
                          _F(GROUP_MA='Group2',
                             MATER=MA2,),),);

• )

課題†

異方性の設定で等方性材料を解く†

• 条件　
  • \( E=7\mathrm{GPa} \)
  • \( ν=0.4 \)
  • \( P=100 \mathrm{N} \)
  • \( l=100 \mathrm{mm} \)
  • \( G=\frac{E}{2(1+ν)} \)
  • \( 断面積A=0.0001\mathrm{m^2} \)

salomeでの\( \sigma_x = -1.0 × 10^{6} \)

手計算での\( \sigma_x = -9.99999 × 10^{5} \)

手計算でのポアソン比\( \nu_{xy} = \nu_{xz} = 0.4 \)

等方性なら誤差ほぼないらしい．

やはり梁の長いほうがLに勝手になるっぽい．

直交異方性材料を圧縮で確かめる†

• ポアソン比を式から確かめる．
• commファイルの中身（フランス語）の意味を調べておく．

直交異方性材料の片持ち梁におけるFEMとティモシェンコ梁(\( v_{T} \))の比較†

\( v_{T} = \frac{pl^{3}}{3EI} + \frac{pl}{kGA} = 0.00598113 (\mathrm{m}) \)

• 条件　
  • \( E=7\mathrm{GPa} \)
  • \( ν=0.4 \)
  • \( P=100 \mathrm{N} \)
  • \( l=100 \mathrm{mm} \)
  • \( k=\frac{5}{6} \)
  • \( G=\frac{E}{2(1+ν)} \)
  • \( 断面積A=0.0001\mathrm{m^2} \)

H断面の片持ち梁を考える．†

• 条件　
  • \( E=6\mathrm{GPa} \)
  • \( ν=0.3 \)
  • \( P=100 \mathrm{N} \)
  • \( l=100 \mathrm{mm} \)
  • \( 断面積A=0.000028\mathrm{m^2} \)

6月20日†

赤：salome，緑：手計算→誤差が大きい何かが違うか（節点数がおおいのでは）

• 拘束面の応力分布

• 一要素隣の応力分布

• 真ん中の応力分布

梁のたわみを理論式（初等梁(\( v_{初} \))とティモシェンコ梁(\( v_{T} \))）と比較する.†

\( v_{初} = \frac{pl^{3}}{3EI} = 6.666667 (\mathrm{m}) \)

\( v_{T} = \frac{pl^{3}}{3EI} + \frac{pl}{kGA} = 6.667187 (\mathrm{m}) \)

• 条件　
  • \( E=6\mathrm{GPa} \)
  • \( ν=0.3 \)
  • \( P=100 \mathrm{N} \)
  • \( l=1000 \mathrm{mm} \)
  • \( k=\frac{5}{6} \)
  • \( G=\frac{E}{2(1+ν)} \)
  • \( 断面積A=0.0001\mathrm{m^2} \)

6月6日†

• 応力を縦軸(z)にして書き換える
• 断面(z=0)を3次元プロットに一緒にプロットする

• 直方体要素で、固定端から1要素となりの断面の応力分布は、どれくらい変わるか

• 梁の真ん中の断面の応力分布はどうか（以上の3箇所を比較）

• 手計算\( \sigma=\frac{M}{I}y \)とどれくらい合うか。手計算で求まる面を3次元プロットにあわせてプロット。（問題：なんか違う…→解決：図心からの距離が間違えていた）

• 固定端部の手計算との比較

• 1要素隣の手計算との比較

• 真ん中の手計算との比較

5月30日†

memo†

• &link(danmen.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/hoka/danmen.f90)から

print*,'# 変位:',sum(v)/size(v)　は変位方向 → z方向への荷重なら print*,'# 変位:',sum(w)/size(w)

print*,szz(i),x(i),y(i)　は奥行き，横，縦 → 課題では print*,sxx(i),y(i),z(i)

! gnuplot> set yrange[] reverse ! gnuplot> set zrange[] reverse　この2行は見たい方向（好みで変更可能）

5月23日（面載荷）†

先週の課題で、四面体要素と立方体要素のそれぞれに対して線形要素と2次要素のそれぞれ4通りを計算してみる． 立方体要素の要素長さは、2mm, 1mm, 0.5mm

• 四面体要素
  • 線形要素

    length(mm)	FEM(m)	相対誤差\( \frac{FEM - v_{初}}{v_{初}} × 100 \)	相対誤差\( \frac{FEM - v_{T}}{v_{T}} × 100 \)
    16	1.869425	72.0	72.0
    8	3.729085	44.1	44.1
    4	4.41786	33.7	33.7
    2	5.932665	11.0	11.0
    1	ムリ	-	-

• 二次要素

  length(mm)	FEM(m)	相対誤差\( \frac{FEM - v_{初}}{v_{初}} × 100 \)	相対誤差\( \frac{FEM - v_{T}}{v_{T}} × 100 \)
  16	6.64958	0.3	0.3
  8	6.66009	0.1	0.1
  4	6.66194	0.1	0.1
  2	ムリ	-	-
  1	ムリ	-	-
  3.5	6.66235	0.1	0.1

• 立方体要素
  • 線形要素

    length(mm)	FEM(m)	相対誤差\( \frac{FEM - v_{初}}{v_{初}} × 100 \)	相対誤差\( \frac{FEM - v_{T}}{v_{T}} × 100 \)
    2	6.52027	2.1	2.2
    1	ムリ	-	-
    0.5	ムリ	-	-

• 二次要素

  length(mm)	FEM(m)	相対誤差\( \frac{FEM - v_{初}}{v_{初}} × 100 \)	相対誤差\( \frac{FEM - v_{T}}{v_{T}} × 100 \)
  2	6.52027	2.1	2.2
  1	ムリ	-	-
  0.5	ムリ	-	-

5月16日（線載荷）†

10mm×10mm断面の角材（ヤング率：6GPa, ポアソン比：0.3）の片持ち梁の 初等梁、ティモシェンコ梁に対する相対誤差を求める．荷重は面荷重で100N. 長さは、7人で、50mm, 100mm, 200mm, 400mm, 800mm, 1000mm, 2000mmを分担． 要素分割は、Lengthが16, 8, 4, 2, 1

後藤さんからの頼まれもの（CLTの図とか）†

端から140mmで拘束しているモデル（本当は135mm）†

• メッシュの図

• mises応力（載荷面上から見た図）

• mises応力（載荷面下から見た図）

135mmで拘束しているモデル（半解析）と実験値との比較†

&link(hikaku.ods,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/fujita/toyoda.ods)

最新の100件