2014/5/3†
孔空き修正
三角孔モデル作成
今後やりたい†
- 三角孔をあける salome fortran
- 孔とせん断補正係数の関係 鋼板のみと鋼板と木材
- 鋼板と木材の場合のティモによる近似
- \( \frac{P \ell^3}{48EI} +\frac{P \ell}{k^* EA} \)でいいのか
- 継手について実験するべき?
- FEMで断面を変えて式を当ててみる
inpファイルを見やすくする†
k2のvineのなかにある.vimrc-ubuntuを
.vimrc に .vimrc-ubuntuみたいのをいれるといい
STEP,NLGEOMについて†
ERROR: increment size smaller than minimum†
best solution and residuals are in the frd file
- cgxで見るとentityの上にDISPとFORCみたいのがある。
モデル図†
穴開き補剛材なし†
kの求め方†
長方形断面†
せん断力による仕事
cgxについて 2013/10/11†
- c3d4などでダイヤカットなどを作ると輪郭線?がはいったりはいらなかったりする。
水平補剛材ありモデルの解析†
2013/07/10(実験データ) 2013/10/1†
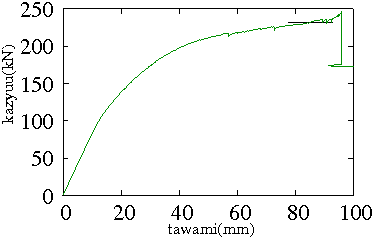
予備試験†
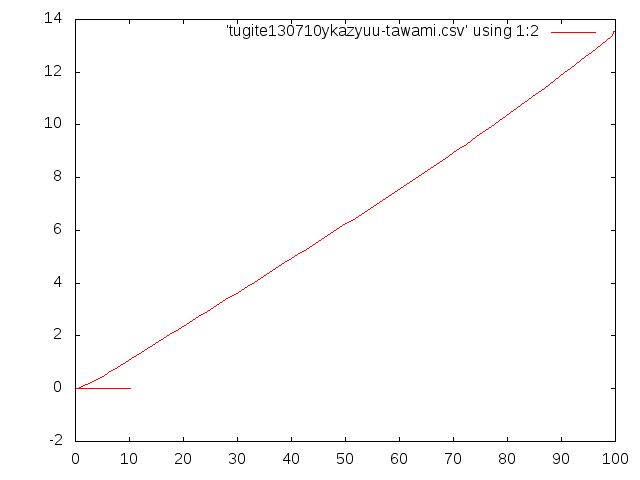
片持ち梁等分布荷重たわみ公式 導出法による違い 2013/9/4†
- \( M_{(z)} \)=\( \frac{-qz^2}{2} \)+\( q \)\( \ell \)\( z \)-\( \frac{q\ell^2}{2} \)
- \( -EIv'' \)=\( \frac{-qz^2}{2} \)+\( q \)\( \ell \)\( z \)-\( \frac{q\ell^2}{2} \)s
- \( -EIv' \)=\( \frac{-qz^3}{6} \)+\( \frac{q\ell z^2}{2} \)-\( \frac{q\ell^2z}{2} \)+A
- \( -EIv \)=\( \frac{-qz^4}{24} \)+\( \frac{q\ell z^3}{6} \)-\( \frac{q\ell^2z^2}{4}+A \)z+B
- 境界条件z=0でv=0よりB=0
- 境界条件z=0で\( \theta \)=0と\( \theta_{(z)} \)=\( \frac{M_{(z)}'}{kGA} \)-\( v' \)より
- \( \frac{A}{EI} \)=-\( \frac{ql}{kGA} \)
- \( v_{(z)} \)=\( \frac{1}{24EI} \)(\( qz^4 \)-\( 4q\ell z^3 \)+\( 6q\ell^2z^2 \))+\( \frac{q\ell z}{kGA} \)
- z=\( \ell \)のとき
たわみ=\( \frac{q\ell^4}{8EI} \)+\( \frac{q\ell^2}{kGA} \)
単位荷重法†
- 曲げたわみを求める
\( $M_{(x)}=-\frac{qx^2}{2} +p\ell x-\frac{q\ell^2}{2} \)$
\( $\overline{M_{(x)}}=x-\ell \)$
\( $v_b=\int_{0}^{\ell}\frac{M_{(x)} \overline{M_{(x)}}}{EI} \)$
\( $v_b=\frac{2}{EI}\int_{0}^{\frac{\ell}{2}}(-\frac{qx^2}{2} +q\ell x -\frac{q\ell^2 }{2})(x-\ell) \)$
\( $v_b=\frac{2}{EI}[-\frac{qx^4}{8} +\frac{q\ell x^3}{2} -\frac{3q\ell^2 x^2}{4}+\frac{q\ell^3}{2}]^\ell _0 \)$
\( $v_b=\frac{q\ell^4}{8EI} \)$
- せん断たわみを求める
\( $S_{(x)}=q\ell -qx \)$
\( $\overline{S_{(x)}}=1 \)$
\( $v_s=\int_{0}^{\ell}\frac{S_{(x)} \overline{S_{(x)}}}{kGA} \)$
\( $v=\frac{q\ell^2}{2kGA} \)$
- たわみを求める
\( $v=v_b +v_s \)$
\( $v=\frac{q\ell^4}{8EI}+\frac{q\ell^2}{2kGA} \)$
単位法線ベクトルの導出-2013/9/02†
- 説明図
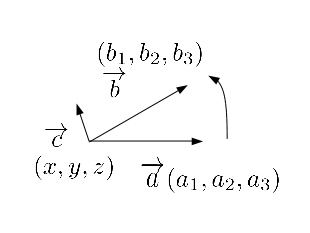
- 図のような単位法線ベクトル\( \overrightarrow{c} \)を求める
- \( \overrightarrow{c} \)=(x,y,z)は\( \overrightarrow{a} \)=(\( a_1,a_2,a_3 \)),\( \overrightarrow{b} \)=(\( b_1,b_2,b_3 \))
- 両方に垂直なベクトルなので内積が0になるため
\( $a_1 x+a_2 y+a_3 z=0・・・(1) \)$
\( $b_1 x+b_2 y+b_3 z=0・・・(2) \)$
- \( \overrightarrow{c} \)の大きさは1なので
\( $x^2 +y^2 +z^2=1・・・(3) \)$
- \( 式(1)\times 3-式(1)\times 3=0 \)
\( $(a_1 b_3 -b_1 a_3)x+(a_2 b_3-b_2 a_3)y=0 \)$
\( $y=\frac{b_1 a_3 -a_1 b_3}{a_2 b_3 -b_2 a_3}x・・・(4) \)$
- (1)に(4)を代入
\( $a_1 x+a_2\frac{b_1 a_3 -a_1 b_3}{a_2 b_3 -b_2 a_3}x+a_3 z=0 \)$
\( $\frac{a_1 a_2 b_3 -a_1 a_3 b_2 +a_2 a_3 b_1 -a_1 a_2 b_3}{a_2 b_3 -b_2 a_3}x+a_3 z=0 \)$
\( $\frac{a_2 a_3 b_1 -a_1 a_3 b_2}{a_2 b_3 -b_2 a_3}x=-a_3 z \)$
\( $x=\frac{a_2 b_3 -b_2 a_3}{a_1 b_2 -b_1 a_2}z・・・(5) \)$
- (4)に(5)を代入
\( $y=\frac{b_1 a_3 -a_1 b_3}{a_1 b_2 -b_1 a_2}z・・・(6) \)$
- (3)に(5),(6)を代入
\( $z=\frac{a_1 b_2 -a_2 b_1}{(a_2 b_3 -a_3 b_2)^2+(a_3 b_1 -a_1 b_3)^2 +(a_1 b_2 -a_2 b_1)^2}・・・(7) \)$
- (5),(6)に(7)を挿入
\( $x=\frac{a_2 b_3 -a_3 b_2}{(a_2 b_3 -a_3 b_2)^2+(a_3 b_1 -a_1 b_3)^2 +(a_1 b_2 -a_2 b_1)^2} \)$
\( $y=\frac{a_3 b_1 -a_1 b_3}{(a_2 b_3 -a_3 b_2)^2+(a_3 b_1 -a_1 b_3)^2 +(a_1 b_2 -a_2 b_1)^2} \)$
- となる。
水平補剛材オンサイト計算†
中立軸計算†

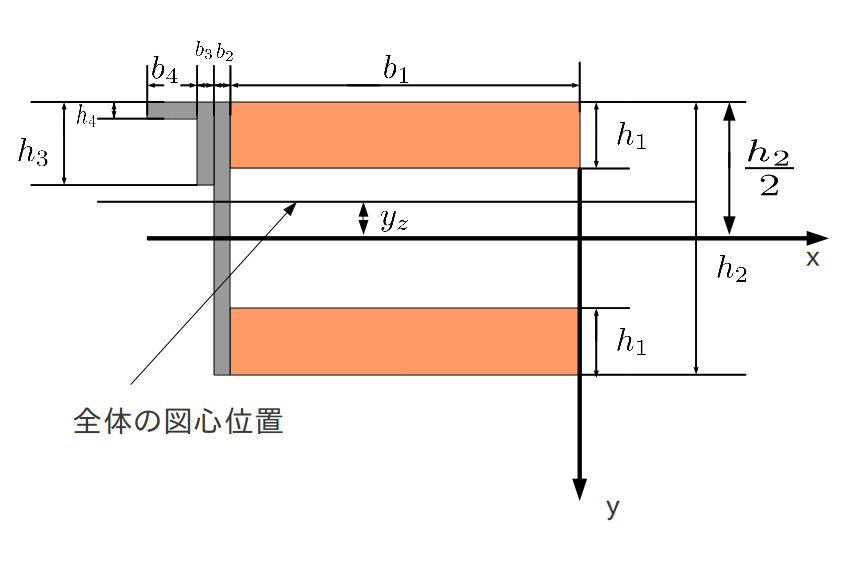
断面1について†
- まず木材部分の断面1次モーメント\( B_木 \)を求める。
\( $B_木={b_1}(\int_{-c_1}^{h_1-c_1}ydy+\int_{h_2-c_1-h_1}^{h_2-c_1}ydy) \)$
\( $B_木=-2b_1 h_1 c_1+b_1 h_1 h_2 \)$
- 次に鋼部分の断面1次モーメント\( B_鋼 \)をもとめる。
- 木材と鋼のヤング率比$\frac{E_鋼}{E_木}=nとする。
\( $B_鋼=n(b_2\int_{-c_1}^{h_2-c}ydy+b_3\int_{-c_1}^{h_3-c_1}ydy+b_4\int_{-c_1}^{h_4-c_1}ydy) \)$
\( $B_鋼=-n(b_2 h_2 +b_3 h_3 +b_4 h_4 )c_1+\frac{n}{2}(b_2 h_2 ^2 +b_3 h_3 ^2 +b_4 h_4 ^2) \)$
- ふたつをたしてBを求める
\( $B=B_木+B_鋼 \)$
- B=0より、c_1=の形に変形
\( $c_1=\frac{b_1 h_1 h_2 +\frac{n}{2}(b_2 h_2 ^2 +b_3 h_3 ^2 +b_4 h_4 ^2)}{2h_1 b_1 +n(b_2 h_2 + b_3 h_3 +b_4 h_4)} \)$
- 実験のモデルの値を代入すると
\( c_1=219.54 \)(mm)
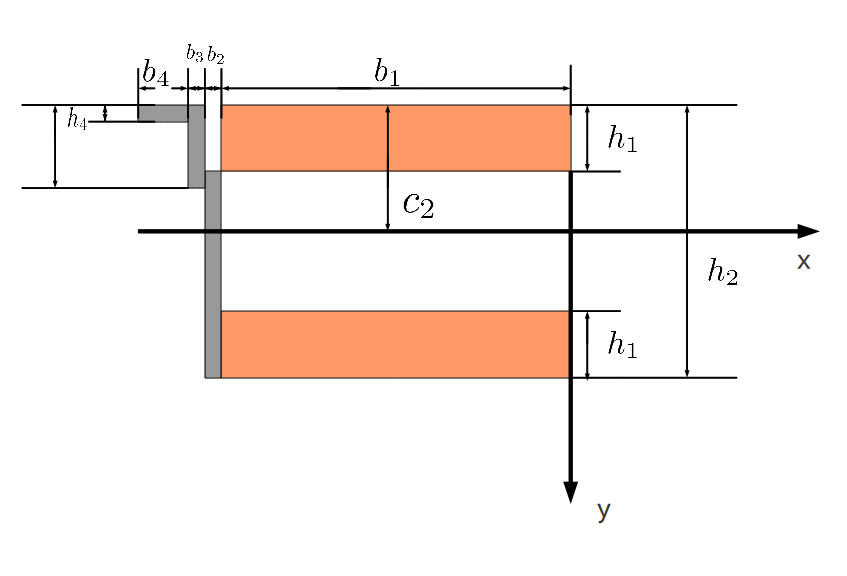
断面1について(2)†
- 断面1次モーメントBは次の式で表される。
\( $B=\Sigma E_i A_i y_i \)$
- ここで\( E_1 \)はヤング率、\( A_i \)は面積、\( y_i \)は図心位置のy座標
- \( B=\Sigma E_i A_i y_z \)で表すこともできて、
- \( \Sigma E_i A_i y_z=\Sigma E_i A_i y_i \)となる。
- \( y_z \)は全体の図心位置のy座標である
\( $y_z=\frac{\Sigma E_i A_i y_i}{\Sigma E_i A_i} \)$
- 分子部分は補剛材のところ以外0になるので
\( $y_z=\frac{E_鋼 (b_3 h_3(-\frac{h_2}{2}+\frac{h_3}{2}) +b_4 h_4(-\frac{h_2}{2}+\frac{h_4}{2}))}{E_鋼(b_2 h_2 +b_3 h_3 +b_4 h_4)+E_木 2b_1 h_1} \)$
\( y_z=-30.46 \)(mm)
\( $c_1+\rvert{y_z}\lvert=\frac{h_2}{2} \)$
\( $219+31=250 \)$
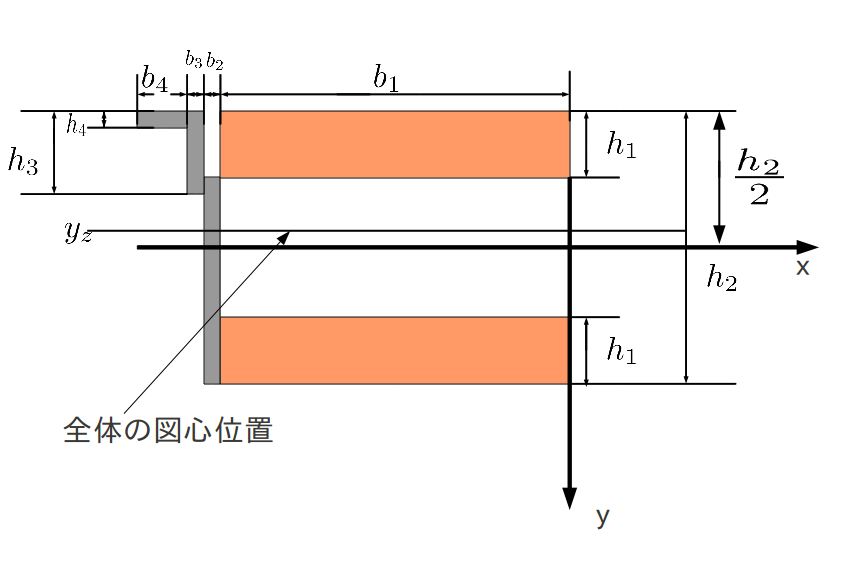
断面2について†
- 断面1と同じようにやっていくと
\( $c_1=\frac{b_1 h_1 h_2 +\frac{n}{2}(b_2 h_2 ^2 -b_2 h_1 ^2 +b_3 h_3 ^2 +b_4 h_4 ^2)}{2h_1 b_1 +n(b_2 h_2 -b_2 h_1 + b_3 h_3 +b_4 h_4)} \)$
- 実験のモデルの値をいれると
\( c_1= \)
中立軸がきまってからの曲げ剛性やせん断剛性の求め方†
木材の曲げ剛性†
\( $E_{木}I_{木} =E_{木} \times2b_1 \frac{(\frac{h_2}{2}-c)^3-(\frac{h_2}{2}-c-h_1)^3+(\frac{h_2}{2}+c)^3-(\frac{h_2}{2}+c-h1)^3}{3} \)$
鋼板の曲げ剛性(断面1)†
\( $E_{鋼}I_{鋼}=2E_{鋼}\times\frac{ b_2((\frac{h_2}{2}-c_1)^3+(\frac{h_2}{2}+c_1)^3)+b_3((\frac{h_2}{2}-c_1)^3-(\frac{h_2}{2}-c_1-h_3)^3)+b_4((\frac{h_2}{2}-c_1)^3-(\frac{h_2}{2}-c_1-h_4)^3)}{3} \)$
折り紙関係†
ダイヤカットの形の決まり方†
横幅s、高さhの長方形からダイヤカット円筒を作る。
周方向分割数をm、高さ方向分割数をnとする。
ダイヤカットは正m角形を基本形としていて、
偶数段と奇数段とでは\( \frac{\pi}{m} \)だけずれている。
このm角形の一辺の長さは\( \frac{s}{m} \)で、
外接円の半径rを用いて、\( \frac{s}{m}=2rsin\frac{\pi}{m} \)で
表せるので、これを変形して\( r=\frac{s}{2msin\frac{\pi}{m}} \)
となる。
ダイヤカットは三角形が並んで出来ている。
その三角形の高さは\( \frac{h}{n} \)となり。
それは正m角形の一辺の中点と一段上の点を結んだ線分で
その線分とxy平面とのなす角を\( \psi \)とおく。
その線分の水平成分をwとおくと、
\( w=r(1-cos\frac{\pi}{m}) \)となり
\( cos\psi=\frac{nw}{h} \)
\( cos\psi=\frac{ns(1-cos\frac{\pi}{m})}{2hmsin\frac{\pi}{m}} \)となる。
\( \psi=arccos\frac{ns(1-cos\frac{\pi}{m})}{2hmsin\frac{\pi}{m}} \)となる。
ダイヤカットの一段の高さを\( h_1 \)とすると、
\( h_1=\frac{hsin\psi}{n} \)となる。
蛇腹折の形の決まり方†
横幅s、高さhの長方形から蛇腹折円筒を作る。
周方向分割数をm、高さ方向分割数をnとする。
初期高さをaとする。
蛇腹折は上から見ると正m角形を基本形としていて、
一辺の長さは\( \frac{s}{m} \)で、外接円の半径rを用いて、
\( \frac{s}{m}=2rsin\frac{\pi}{m} \)で表せるので、
これを変形して\( r=\frac{s}{2msin\frac{\pi}{m}} \)となる。
この正m角形のm個ある点を外接円上を移動させて蛇腹折を作る。
奇数段目の時は、奇数番目の点の時は反時計回りを正として、
ある角度\( \theta \)動かして、偶数番目の時は\( -\theta \)動かす。
偶数段目の時は、奇数番目で\( -\theta \)、偶数番目で\( \theta \)動かす。
この\( \theta \)はm、n、a、s、hで自動的に決まる。
一段の高さは$\frac{ah}{n}となる。
- \( \theta \)を導く
上から見た時内側に小さな正m角形ができる。
この一辺をbとすると、
蛇腹折の辺の長さは\( b+v \)と\( b+u \)で表すことが出来る。
外側には台形ができる。
その台形の高さは\( \frac{h}{n} \)
でそのxy平面への射影の長さをwとする。
この台形とxy平面とのなす角を\( \psi \)とする。
- \( \frac{hsin\psi}{n}=\frac{ah}{n} \)となり、
- \( sin\psi=a \)
- \( \psi=arcsin(a) \)となる。
- \( w=\frac{hcos\psi}{n} \)となる。
- \( sin\frac{2\pi}{m}=\frac{w}{v} \)より、
- \( v=\frac{w}{sin\frac{2\pi}{m}} \)となる。
上から見た時、台形の斜辺の長さは\( 2rsin\theta \)なので
- \( \frac{w}{cos\frac{\pi}{m}}=2rsin\theta \)となり
- \( sin\theta=\frac{w}{2r cos\frac{\pi}{m}} \)となるので
- \( \theta=arcsin\frac{w}{2r cos\frac{\pi}{m}} \)となる。
板の厚さについて†
最初は二つの半径の差を厚さとしていたが
その大きさは出来る台形の斜辺の長さなので
台形の高さを厚さにするようにする。
外側の外接円の半径を\( r_1 \)、内側の外接円の半径を\( r_2 \)とする
sを与えてrを求めるので\( s_2 \)を決めるために、
- \( s_1-s_2 \)の関係を求める。
- \( r_1=\frac{s_1}{2msin\frac{\pi}{m}} \)
- \( r_2=\frac{s_2}{2msin\frac{\pi}{m}} \)となる。
- 台形の高さxは(xは自分で設定)
- \( x=\frac{s_1-s_2}{2mtan\frac{\pi}{m}} \)となるので
- \( 2mxtan\frac{\pi}{m}=s_1-s_2 \)より
- \( s_2=s_1-2mxtan\frac{\pi}{m} \)となる。
- \( r_2=r_1-\frac{x}{cox\frac{\pi}{m}} \)となる。
プログラムでは\( s_2 \)を与えずに\( r_2 \)だけ与えてもいい。
実験データ†
木材の長さとヤング率昔(水平補剛材なし)†
| 番号 | 長さ | ヤング率(GPa) | ヤング率*長さ/(6300*14) |
| 1 | 8.14 | 1400 | 0.129206349206349 |
| 2 | 5.99 | 1400 | 0.0950793650793651 |
| 3 | 6.99 | 1400 | 0.110952380952381 |
| 4 | 7.41 | 1400 | 0.117619047619048 |
| 5 | 7.59 | 1400 | 0.12047619047619 |
| 6 | 6.99 | 1400 | 0.110952380952381 |
| 7 | 6.71 | 1400 | 0.106507936507937 |
| 8 | 6.37 | 1400 | 0.101111111111111 |
| 9 | 6.54 | 1400 | 0.103809523809524 |
| 10 | 6.85 | 1400 | 0.108730158730159 |
| 11 | 7.31 | 2800 | 0.232063492063492 |
| 12 | 4.61 | 2800 | 0.146349206349206 |
| 13 | 6.54 | 2800 | 0.207619047619048 |
| 14 | 6.04 | 2800 | 0.191746031746032 |
| 15 | 4.55 | 2800 | 0.144444444444444 |
| 16 | 6.21 | 2800 | 0.197142857142857 |
| 17 | 6.94 | 2800 | 0.22031746031746 |
| 18 | 10.41 | 2800 | 0.33047619047619 |
| 19 | 5.96 | 2800 | 0.189206349206349 |
| 20 | 7 | 3500 | 0.277777777777778 |
| 21 | 8.01 | 3500 | 0.317857142857143 |
| 22 | 6.6 | 3500 | 0.261904761904762 |
| 23 | 7.89 | 3500 | 0.313095238095238 |
| 24 | 7.24 | 3500 | 0.287301587301587 |
| 25 | 5.72 | 3500 | 0.226984126984127 |
| 26 | 6.87 | 3500 | 0.272619047619048 |
| 27 | 7.55 | 3500 | 0.299603174603175 |
| 28 | 4.89 | 3500 | 0.194047619047619 |
| 29 | 7.44 | 3500 | 0.295238095238095 |
| 30 | 9.36 | 3500 | 0.371428571428571 |
| 31 | 7.13 | 3500 | 0.282936507936508 |
| 32 | 8.61 | 3500 | 0.341666666666667 |
| 33 | 5.61 | 3500 | 0.222619047619048 |
| 228.07 | | 6.92888888888889 |
木材の長さとヤング率2013/7/10†
| ID | 長さ | ヤング率*100(GPa) | ヤング率(GPa) | ヤング率*長さ/(7300*14) |
| 1 | 1460 | 671 | 6.71 | 0.0958571428571429 |
| 2 | 2920 | 790 | 7.9 | 0.225714285714286 |
| 3 | 2920 | 956 | 9.56 | 0.273142857142857 |
| 4 | 2190 | 856 | 8.56 | 0.183428571428571 |
| 5 | 2920 | 938 | 9.38 | 0.268 |
| 6 | 2190 | 631 | 6.31 | 0.135214285714286 |
| 7 | 2920 | 753 | 7.53 | 0.215142857142857 |
| 8 | 2920 | 966 | 9.66 | 0.276 |
| 9 | 1460 | 492 | 4.92 | 0.0702857142857143 |
| 10 | 1460 | 835 | 8.35 | 0.119285714285714 |
| 11 | 2920 | 1030 | 10.3 | 0.294285714285714 |
| 12 | 2920 | 796 | 7.96 | 0.227428571428571 |
| 13 | 2190 | 656 | 6.56 | 0.140571428571429 |
| 14 | 2920 | 891 | 8.91 | 0.254571428571429 |
| 15 | 2190 | 726 | 7.26 | 0.155571428571429 |
| 16 | 2920 | 732 | 7.32 | 0.209142857142857 |
| 17 | 2920 | 877 | 8.77 | 0.250571428571429 |
| 18 | 1460 | 646 | 6.46 | 0.0922857142857143 |
| 19 | 1460 | 617 | 6.17 | 0.0881428571428572 |
| 20 | 2920 | 783 | 7.83 | 0.223714285714286 |
| 21 | 2920 | 816 | 8.16 | 0.233142857142857 |
| 22 | 2190 | 539 | 5.39 | 0.1155 |
| 23 | 2920 | 935 | 9.35 | 0.267142857142857 |
| 24 | 2190 | 632 | 6.32 | 0.135428571428571 |
| 25 | 2920 | 971 | 9.71 | 0.277428571428571 |
| 26 | 2920 | 888 | 8.88 | 0.253714285714286 |
| 27 | 1460 | 698 | 6.98 | 0.0997142857142857 |
| 28 | 1460 | 739 | 7.39 | 0.105571428571429 |
| 29 | 2920 | 548 | 5.48 | 0.156571428571429 |
| 30 | 2920 | 665 | 6.65 | 0.19 |
| 31 | 2190 | 634 | 6.34 | 0.135857142857143 |
| 32 | 2920 | 892 | 8.92 | 0.254857142857143 |
| 33 | 2190 | 569 | 5.69 | 0.121928571428571 |
| 34 | 2920 | 644 | 6.44 | 0.184 |
| 35 | 2920 | 970 | 9.7 | 0.277142857142857 |
| 36 | 1460 | 658 | 6.58 | 0.094 |
| 37 | 1460 | 750 | 7.5 | 0.107142857142857 |
| 38 | 2920 | 692 | 6.92 | 0.197714285714286 |
| 39 | 2920 | 725 | 7.25 | 0.207142857142857 |
| 40 | 2190 | 817 | 8.17 | 0.175071428571429 |
| 41 | 2920 | 521 | 5.21 | 0.148857142857143 |
| 42 | 2190 | 737 | 7.37 | 0.157928571428571 |
| 合計 | | | | 7.69421428571428 |
- 平均のヤング率=7.69421428571428GPa
cowperのkとFEMのkを比較†
s6とc3d4での違い†
kの算出断面についての調査 2013/7/30くらい†
- 箱型断面が並んでいる時一つの箱を取り出して計算している。
- FEMでといてみてそのようになるか調べる
応急橋の箱型断面の場合(材料は鋼材)†
| 箱断面の数 | たわみ | せん断たわみ | k |
| 1 | 2.77171 | 0.2456 | 0.3243 |
| 2 | 2.76543 | 0.2393 | 0.3329 |
| 3 | 2.75925 | 0.2331 | 0.3418 |
| 4 | 2.75294 | 0.2268 | 0.3513 |
| ティモ | 3.04547 | 0.51947 | 0.15340 |
応急橋の箱型断面と同じサイズで板の厚さを揃えた場合†
| 箱断面の数 | たわみ | せん断たわみ | k |
| 1 | 8.18437 | 0.293545 | 0.78575 |
| 2 | 8.17320 | 0.282375 | 0.81683 |
| 3 | 8.16237 | 0.271545 | 0.84941 |
| 4 | 8.15148 | 0.260655 | 0.884900 |
| ティモ | 8.301927 | 0.41192 | 0.56106 |
2013/7/16 オンサイト ティモシェンコ理論値比較 実際の断面と厚さ同じ場合(9mm)の比較†
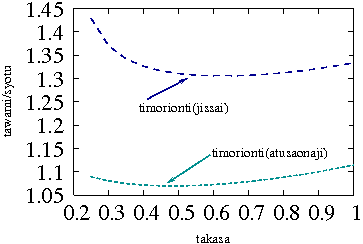
オンサイトグラフ 2013/7/2†
片持ち†
ティモシェンコとの比較 初等梁理論値で割ってせん断の大きさを見る†
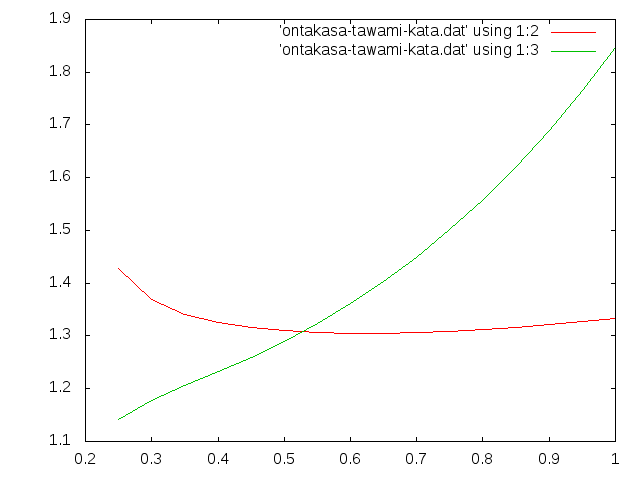
等曲げ†
ティモシェンコとの比較 初等梁理論値で割ってせん断の大きさを見る†
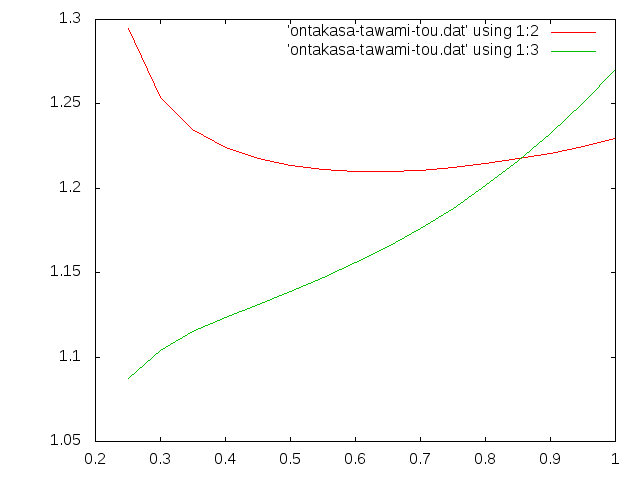
データ処理の仕方†
- 片持ち梁 断面の変位を平均する
- 3点曲げ、等曲げ 荷重の一番下の節点の変位を平均する
実験データ†
オンサイト†
荷重ー変位関係†
中央載荷の場合(データ03)†
| 荷重(kN) | 端5番変位(mm) | 7と5の間変位6番(mm) | 真ん中7番変位(mm) | 7と9の間変位8番(mm) | 端9番変位(mm) | 平均(mm) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.5 | 0.04 | 0.03 | 0.03 | 0.04 | 0.04 | 0.036 |
| 0.9 | 0.07 | 0.06 | 0.06 | 0.06 | 0.07 |
| 1.9 | 0.13 | 0.12 | 0.13 | 0.13 | 0.14 |
| 5 | 0.34 | 0.32 | 0.34 | 0.34 | 0.37 | 0.342 |
| 10.2 | 0.69 | 0.65 | 0.68 | 0.7 | 0.76 | 0.696 |
| 20 | 1.35 | 1.31 | 1.34 | 1.36 | 1.47 | 1.366 |
| 29.8 | 2.02 | 1.96 | 1.99 | 2.02 | 2.18 |
| 40.1 | 2.72 | 2.65 | 2.68 | 2.73 | 2.9 |
| 50 | 3.42 | 3.33 | 3.35 | 3.4 | 3.61 | 3.422 |
| 60.2 | 4.13 | 4.01 | 4.03 | 4.09 | 4.32 |
| 70.3 | 4.9 | 4.76 | 4.78 | 4.84 | 5.1 |
| 80.1 | 5.54 | 5.36 | 5.39 | 5.45 | 5.74 | 5.496 |
| 90.1 | 6.3 | 6.09 | 6.11 | 6.18 | 6.51 |
| 95.1 | 6.69 | 6.45 | 6.48 | 6.55 | 6.9 |
| 98.3 | 6.93 | 6.68 | 6.71 | 6.79 | 7.15 |
| 99.8 | 7.05 | 6.79 | 6.82 | 6.9 | 7.28 |
| 100 | 7.07 | 6.82 | 6.84 | 6.92 | 7.3 | 6.99 |
荷重ー変位関係図
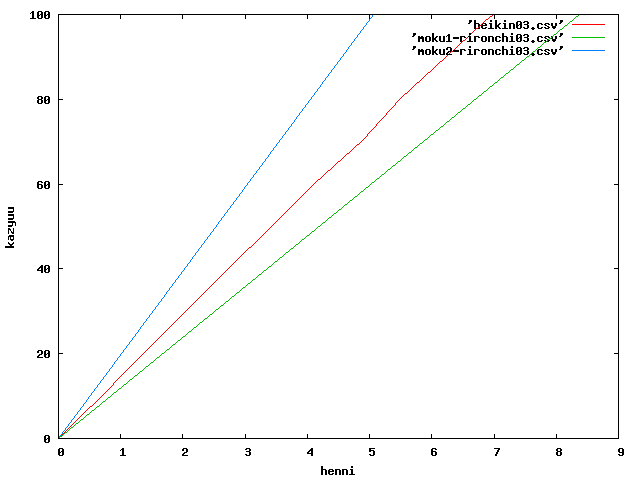
等曲げ載荷の場合(データ05)†
| 荷重(kN) | 端5番変位(mm) | 7と5の間変位6番(mm) | 真ん中7番変位(mm) | 7と9の間変位8番(mm) | 端9番変位(mm) |
| 1 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
| 3 | 0.09 | 0.09 | 0.09 | 0.1 | 0.1 |
| 7 | 0.21 | 0.21 | 0.22 | 0.23 | 0.25 |
| 10.4 | 0.32 | 0.31 | 0.33 | 0.35 | 0.38 |
| 15.1 | 0.46 | 0.45 | 0.48 | 0.5 | 0.55 |
| 20.7 | 0.65 | 0.63 | 0.66 | 0.68 | 0.74 | 0.672 |
| 25.6 | 0.82 | 0.79 | 0.82 | 0.84 | 0.9 |
| 30.2 | 0.97 | 0.94 | 0.97 | 0.99 | 1.06 |
| 40.1 | 1.31 | 1.26 | 1.28 | 1.3 | 1.37 | 1.304 |
| 60.1 | 1.98 | 1.9 | 1.9 | 1.92 | 2.02 | 1.944 |
| 81 | 2.65 | 2.55 | 2.55 | 2.58 | 2.7 | 2.606 |
| 100.5 | 3.27 | 3.15 | 3.15 | 3.19 | 3.33 | 3.218 |
| 110.4 | 3.59 | 3.46 | 3.46 | 3.51 | 3.66 |
| 120.4 | 3.92 | 3.78 | 3.78 | 3.83 | 4 | 3.862 |
| 130.7 | 4.27 | 4.12 | 4.12 | 4.19 | 4.37 |
| 139.8 | 4.59 | 4.44 | 4.44 | 4.51 | 4.7 | 4.536 |
応急橋†
3点曲げ試験†
| 荷重 | たわみ平均(mm) |
| 0 | 0 |
| 5.01 | 0.7105 |
| 10.01 | 1.406167 |
| 15.02 | 2.099167 |
| 20.01 | 2.794833 |
| 25.16 | 3.527667 |
| 30.07 | 4.23933 |
| 35.17 | 4.995 |
| 40.16 | 5.7645 |
等曲げ試験†
| 荷重 | たわみ平均(mm) |
| 0 | 0 |
| 10.01 | 0.897 |
| 19.97 | 1.7715 |
| 30.23 | 2.68116667 |
| 40.1 | 3.5716667 |
| 50.1 | 4.49316667 |
| 60.13 | 5.4495 |
pcゼミ†
salomeのモデル†
- b=1.0d-3m h=1.0d-3 ell=1.0d-1 E=206.0GPa P=1N
| 要素数 | たわみ | 誤差(%) |
| 136 | 7.5275E-05 | -9.96123E+01 |
| 264 | 3.0485E-04 | -9.84300E+01 |
| 1905 | 4.0626E-03 | -7.90776E+01 |
| 4041 | 9.7070E-03 | -5.00090E+01 |
| 17017 | 1.4996E-02 | -2.27706E+01 |
| 38422 | 1.6416E-02 | -1.54576E+01 |
| 268932 | 1.8652E-02 | -3.94220E+00 |
| 367012 | 1.8759E-02 | -3.39115E+00 |
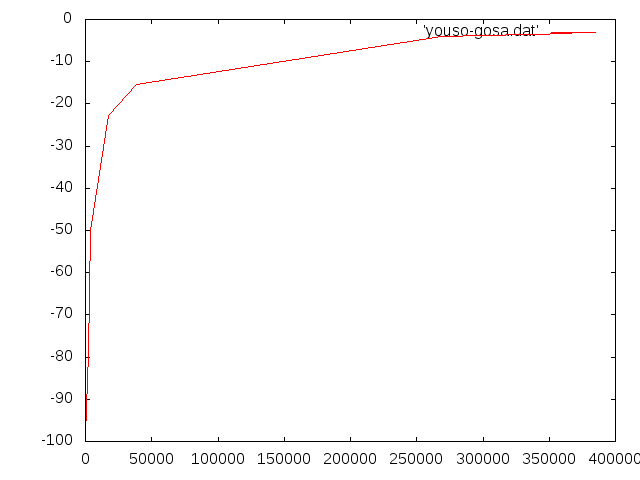
- b=1.0d-3m h=5.0d-3 ell=1.0d-1 E=206.0GPa
156, 1.5417E-05,-9.00753E+01
| 609 | 6.2254E-05 | -5.99240E+01 |
| 2407 | 1.3242E-04 | -1.47546E+01 |
| 9279 | 1.4900E-04 | -4.08125E+00 |
| 38043 | 1.5232E-04 | -1.94400E+00 |
| 40732 | 1.5242E-04 | -1.87962E+00 |
| 211718 | 1.5436E-04 | -6.30750E-01 |
| 222084 | 1.5441E-04 | -5.98562E-01 |
| 236130 | 1.5441E-04 | -5.98562E-01 |
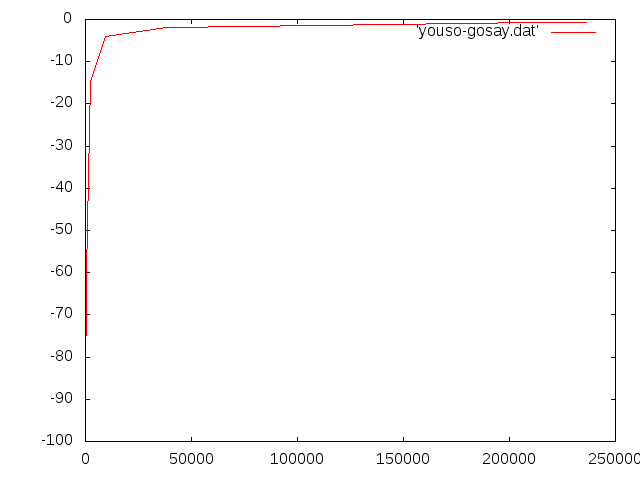
- b=5.0d-3m h=1.0d-3 ell=1.0d-1 E=206.0GPa
| 要素数 | たわみ | 誤差(%) |
| 144 | 1.9649E-05 | -9.94940E+01 |
| 609 | 1.2934E-04 | -9.66695E+01 |
| 2409 | 7.5411E-04 | -8.05817E+01 |
| 8730 | 1.2631E-03 | -6.74752E+01 |
| 36063 | 1.7386E-03 | -5.52311E+01 |
| 30892 | 1.3836E-03 | -6.43723E+01 |
| 211954 | 3.3514E-03 | -1.37015E+01 |
| 220355 | 3.3584E-03 | -1.35212E+01 |
| 239932 | 3.3640E-03 | -1.33770E+01 |
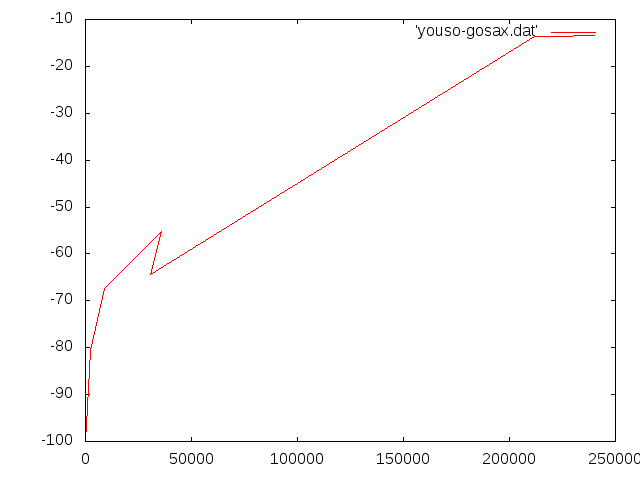
fortranのモデル†
- b=1.0d-3m h=1.0d-3 ell=1.0d-1 E=206.0GPa
| nz | たわみ | 誤差(%) |
| 2 | 2.0172d-5 | -9.98961d1 |
| 4 | 8.0424d-5 | -9.95858d1 |
| 8 | 3.1764d-4 | -9.83642d1 |
| 16 | 1.2103d-3 | -9.3764d1 |
| 32 | 4.0737d-3 | -7.90204d1 |
| 64 | 9.9827d-3 | -4.85891d1 |
| 125 | 1.5531d-2 | -2.00154d+01 |
| 250 | 1.8238d-2 | -6.07430d+00 |
| 500 | 1.9072d-2 | -1.77920d+00 |
| 1000 | 1.9293d-2 | -6.41050d-01 |
| 2000 | 1.9349d-2 | -3.52650d-01 |
- 誤差の収束
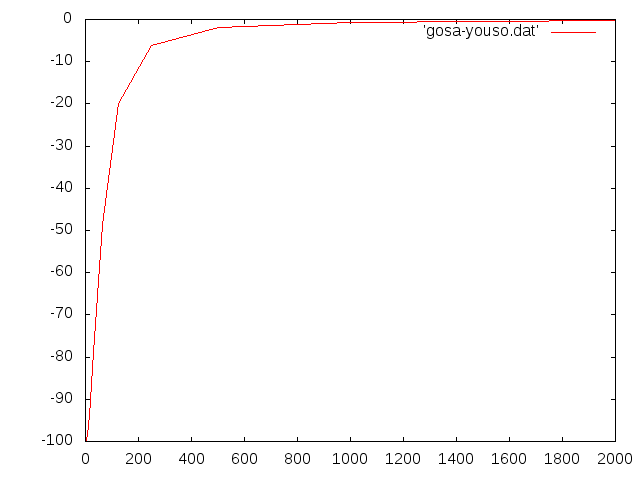
- b=1.0d-3m h=5.0d-3 ell=1.0d-1 E=206.0GPa
| nz | たわみ | 誤差(%) |
| 2 | 3.9300d-6 | -9.74701E+01 |
| 4 | 1.4564d-5 | -9.06244E+01 |
| 8 | 4.5250d-5 | -7.08703E+01 |
| 16 | 9.6163d-5 | -3.80951E+01 |
| 32 | 1.3427d-4 | -1.35637E+01 |
| 64 | 1.4929d-4 | -3.89456E+00 |
| 125 | 1.5363d-4 | -1.10069E+00 |
| 250 | 1.5487d-4 | -3.02437E-01 |
| 500 | 1.5520d-4 | -9.00000E-02 |
| 1000 | 1.5529d-4 | -3.20625E-02 |
| 2000 | 1.5531d-4 | -1.91875E-02 |
- 誤差の収束
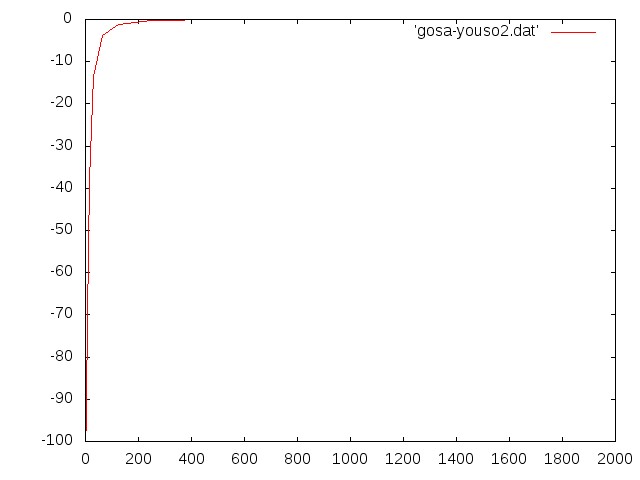
- b=5.0d-3m h=1.0d-3 ell=1.0d-1 E=206.0GPa
| nz | たわみ | 誤差(%) |
| 2 | 4.0348d-6 | -9.98961E+01 |
| 4 | 1.6084d-5 | -9.95858E+01 |
| 8 | 6.3507d-5 | -9.83647E+01 |
| 16 | 2.4171d-4 | -9.37760E+01 |
| 32 | 8.1047d-4 | -7.91304E+01 |
| 64 | 1.9704d-3 | -4.92622E+01 |
| 125 | 3.0428d-3 | -2.16479E+01 |
| 250 | 3.5599d-3 | -8.33258E+00 |
| 500 | 3.7183d-3 | -4.25378E+00 |
| 1000 | 3.7602d-3 | -3.17485E+00 |
| 2000 | 3.7709d-3 | -2.89933E+00 |
- 誤差の収束
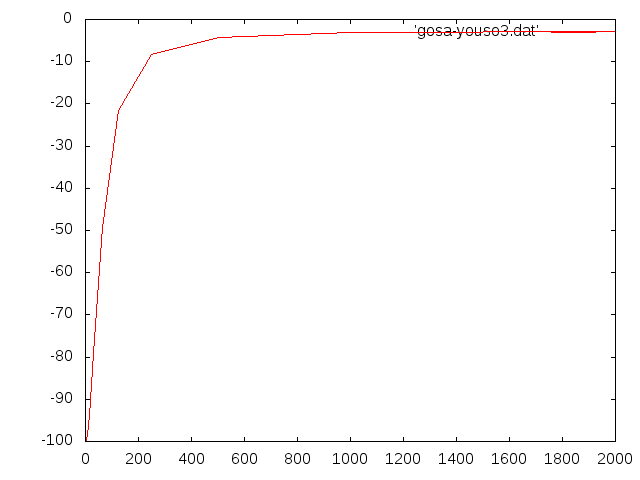
ccx†
- inpファイルで荷重などは14桁までしか読めないので注意
- calculixでは要素数制限ある模様 188928では解けたが190000
では解けなかった。
性能調査†
片持ち梁 集中荷重ティモシェンコと比較k=\( \frac{5}{6} \)†
- b=100mm h=100mm ell=1000mm E=7GPa G=0.46667GPa 理論値0.59714m
| nz | たわみ | たわみ誤差 | k | k誤差 |
| 2 | 2.2248E-1 | -62.7% | -6.1409E-2 | -107% |
| 4 | 4.1956E-1 | -29.7% | -0.14109 | -116% |
| 8 | 5.3932E-1 | -9.68% | -0.66737 | -180% |
| 16 | 5.8112E-1 | -2.68% | 2.211061 | 165.3% |
| 32 | 5.9287E-1 | -0.716% | 0.99939 | 19.92% |
| 64 | 5.9606E-1 | -0.181% | 0.86996 | 4.395% |
| 128 | 5.9696E-1 | -0.0305% | 0.8392945 | 0.715% |
| 256 | 5.9722E-1 | 0.0129% | 0.830833 | -0.299% |
| 512 | 5.9729E-1 | 0.0246% | 0.82858 | -0.569% |
| 1024 | 5.9731E-1 | 0.00280% | 0.27944 | -0.646% |
| 2048 | 5.9731E-1 | 0.00280% | 0.27944 | -0.646% |
- 収束のグラフ
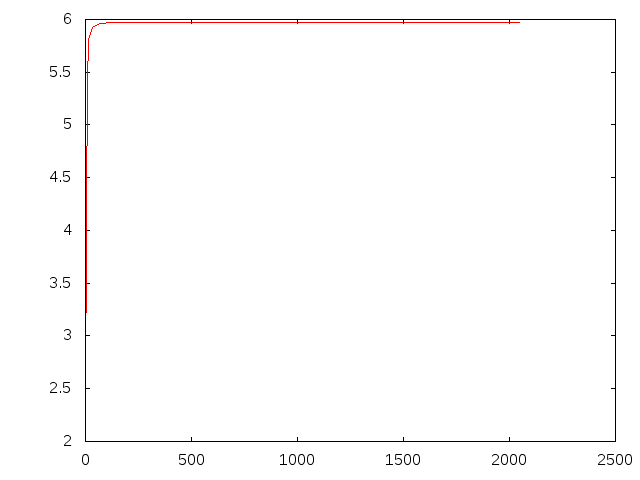
片持ち梁 分布荷重ティモシェンコと比較k=\( \frac{5}{6} \)†
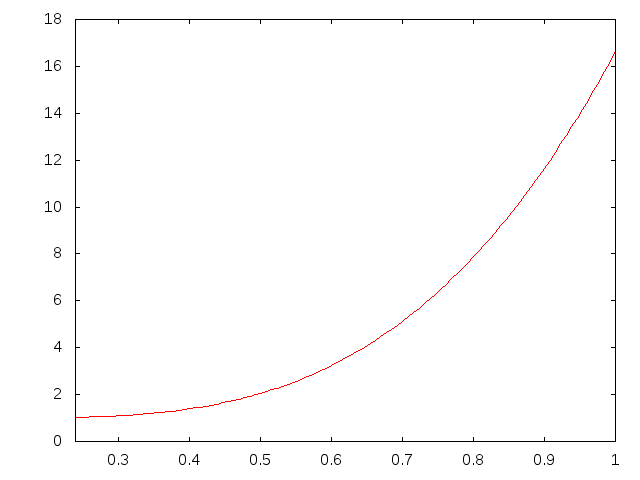
\( \frac{せん断たわみ項}{曲げたわみ項} \)と\( {(\frac{h}{\ell})}^2 \)の比較 k=8.333 G=\( \frac{E}{15} \)†
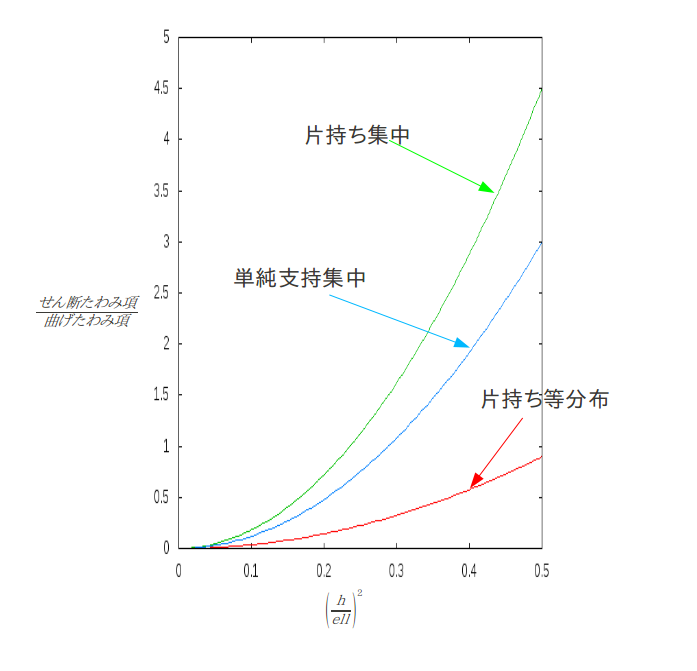
stress†
たわみの他にこんな感じででる。
stresses (elem, integ.pnt.,sxx,syy,szz,sxy,sxz,syz) for set EALL and time 0.1000000E+01
1 1 7.4377E+02 7.3007E+02 5.5169E+03 -2.0140E+01 1.3707E+02 5.8454E+04
1 2 6.6570E+02 6.4050E+02 4.9652E+03 -1.9206E+01 1.2118E+02 5.8451E+04
1 3 2.8079E+02 2.2967E+02 5.1316E+03 -7.5163E+01 1.1161E+02 -3.9701E+04
1 4 2.3486E+02 1.4083E+02 4.5930E+03 -7.1678E+01 9.0776E+01 -3.9704E+04
1 5 7.4374E+02 7.3170E+02 5.5172E+03 3.8285E+01 1.2876E+02 5.8490E+04
1 6 6.6565E+02 6.4211E+02 4.9653E+03 3.9218E+01 1.1346E+02 5.8487E+04
1 7 2.8086E+02 2.3592E+02 5.1337E+03 1.4288E+02 1.0330E+02 -3.9680E+04
1 8 2.3492E+02 1.4706E+02 4.5950E+03 1.4637E+02 8.3056E+01 -3.9683E+04
2 1 -3.1853E+02 -3.9378E+02 1.3563E+03 -7.6906E+01 6.4184E+01 2.5836E+04
2 2 -3.0822E+02 -4.2288E+02 1.1868E+03 -6.8247E+01 4.6576E+01 2.5838E+04
2 3 1.7108E+02 6.7311E+01 1.7365E+03 -2.6646E+01 8.8565E+01 -6.9565E+03
エラー†
*WARNING in noelfiles: parameter not recognized:
POSITION=AVERAGEDATNODES
*WARNING in the input deck. Card image:
*ELFILE,POSITION=AVERAGEDATNODES
梁 たわみ 要素分割の影響(集中荷重)5cm 5cm 100cm 荷重1MN ヤング率206GPa C3D8 ポアソン比 0.3†
| n | nx=4 ny=20 nz | nx=4 ny nz=100 | nx ny=20 nz=100 |
| 2 | 7.8591E-3 -97.5% | 2.9589E-1 -4.76% | 3.0276E-1 -2.55% |
| 4 | 2.9124E-2 -90.6 | 3.0220E-1 -2.73 | 3.0443E-1 -2.01 |
| 8 | 9.0446E-2 -70.9 | 3.0393E-1 -2.17 | 3.0490E-1 -1.86 |
| 16 | 1.9196E-1 -38.2 | 3.0438E-1 -2.03 | 3.0503E-1 -1.82 |
| 20 | | 3.0443E-1 -2.01 | 3.0506E-1 -1.81 |
| 32 | 2.6787E-1 -14.7 | 3.0449E-1 -1.99 | 3.0507E-1 -1.80 |
| 50 | | 3.0452E-1 -1.98 | |
| 64 | 2.9764E-1 -4.20 | | |
| 100 | 3.0443E-1 -2.01 | | |
| 128 | 3.0631E-1 -1.41 | | |
| 256 | 3.0861E-1 -0.67 | | |
| 512 | 3.0925E-1 -0.46 | | |
| 1000 | 3.09371E-1 -0.42 | | |
集中荷重を一箇所にかけたときは精度がいいが面や線にかけるとかなり大きくたわむ
読める桁数の問題だった。
cgxエラー†
mentat†
モデル読み込み†
- 直方体要素ならinpファイルで普通に読み込めて材料や境界条件、
荷重などもすべて読み込める。(異方性についてはまだ不明)解いた結果は近かった)
- shellもS3Rなら読み込める。
構造実験†
グラフ†
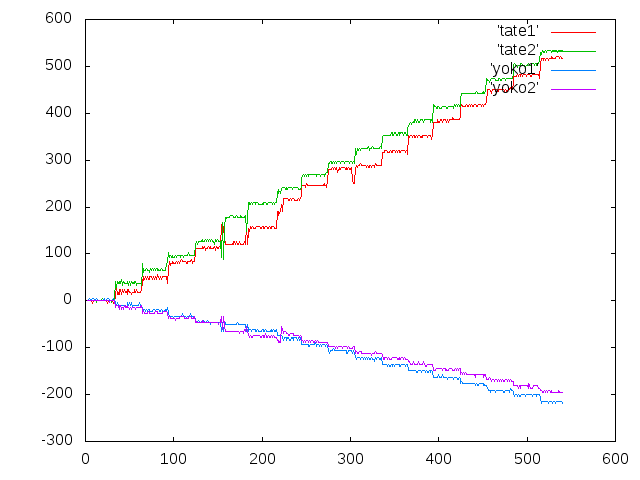
後藤ちゃちゃ(13/2/15)†
- gosaon.f90のk*のBankの式は、分母の3項目\( (60m^{2}n^{2}+40\alpha mn^{2}) \)が抜けているのでは(まあ、これによる差はあまりでないが)。
- 桁高のh(gosaon.f90のh1)は、上下の角材の隙間ではなく、フランジ図心間距離(500-120)だと思います。そうすると、k*が2倍ぐらいになるので、オンサイトのせん断変形の影響は少し小さく(実験値よりちょっと固めぐらいに)ずれるのではないかと思います。計算しなおせますか。
- 更に、k*EAのEAですが、、(EwIw+EsIs)(Aw+As)/(Iw+Is)みたいなことをやってますね。並列合成の(EwAw+EsAs)にしてもらえますか。
- 私が書き換えたプログラム&link(gosaong.f90,http://www.str.ce.akita-u.ac.jp/~gotou/programoj/hari/gosaong.f90)
2012年前期†
| 月 | 火 | 水 | 木 | 金 |
| 1-2 | | | | | |
| 3-4 | 構造力学特論 | 都市システム計画特論 | 建設材料特論 | 交通システム計画特論 | |
| 5-6 | 建設構造工学特論 | 土質力学特論 | 物理学実験 | 英語ゼミ | |
| 7-8 | | | 物理学実験 | | |
2012年後期†
| 月 | 火 | 水 | 木 | 金 |
| 1-2 | | | | | |
| 3-4 | | 環境材料学 | | | |
| 5-6 | 物理学実験 | 福祉のまちづくり特論 | | ゼミ | 木構造工学 |
| 7-8 | 物理学実験 | 構造設計学特論 | | | |
プログラム類†
計算類†
応急橋のせん断補正係数とたわみを出すプログラム†
&link(keioukyuu.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/keisan/keioukyuu.f90)
応急橋の高さとせん断たわみの大きさのグラフデータを作るプログラム†
&link(oukyutakasa.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/keisan/oukyutakasa.f90)
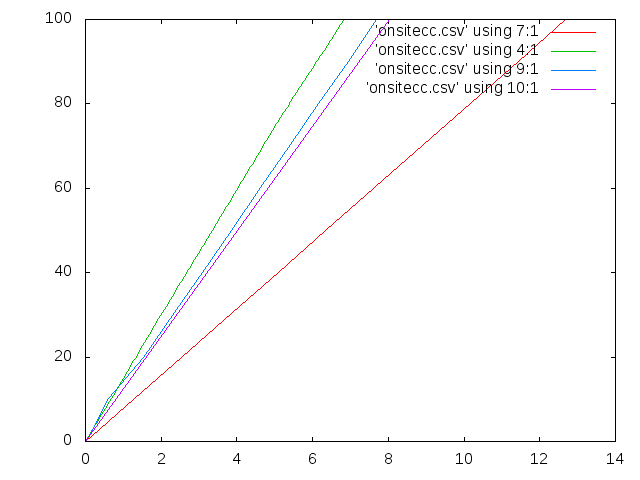
オンサイトのせん断補正係数とたわみを出すプログラム†
&link(keionsite.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/keisan/keionsite.f90)
オンサイトの高さとせん断たわみの大きさのグラフデータを作るプログラム†
&link(onsitetakasa.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/keisan/onsitetakasa.f90)
f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/keisan/hakotakasa.f90)
箱型断面のcowperのkとたわみを出すプログラム†
&link(hakotakasa.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/keisan/hakotakasa.f90)
モデル類†
応急橋片持ちのモデル†
&link(oukyukata.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/oukyukata.f90)
応急橋3点曲げのモデル†
&link(oukyu3ten.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/oukyu3ten.f90)
応急橋等曲げのモデル†
&link(oukyutoumage.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/oukyutoumage.f90)
オンサイト木橋片持ちのモデル†
&link(onsitekata.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/onsitekata.f90)
オンサイト木橋3点曲げモデル†
&link(onsite3ten.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/onsite3ten.f90)
オンサイト木橋3点曲げモデル孔 座屈†
&link(onana3tenza.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/onana3tenza.f90)
オンサイト木橋3点曲げモデル孔補剛 座屈†
&link(onhana3tenza.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/onhana3tenza.f90)
オンサイト木橋等曲げモデル†
&link(onsitetoumage.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/onsitetoumage.f90)
オンサイト木橋3点曲げ 孔空きタイプ†
&link(onana3ten.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/onana3ten.f90)
オンサイト木橋3点曲げ 三角孔空きタイプ†
&link(on3kakuana3ten.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/on3kakuana3ten.f90)
オンサイト木橋3点曲げ 三角孔空きタイプ修正版†
&link(on3kakuana3ten2.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/on3kakuana3ten2.f90)
せん断項についての調査 片持ち木材集中荷重†
&link(katamoku.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/katamoku.f90)
mentatインポート用モデルダイヤカットs3r†
&link(daiyatc.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/daiyatc.f90)
ccx用ダイヤカットs6†
&link(daiyat6c.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/daiyat6c.f90)
ccx用ダイヤカットs6 2.3用†
&link(daiya6h.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/daiya6h.f90)
ccx用ダイヤカットc3d4†
&link(daiyac3d4.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/daiyac3d4.f90)
3dプリンター用ダイヤカット stl†
3dプリンター用のstlファイルを作るプログラム
&link(daiyastl.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/daiyastl.f90)
円筒や角筒を作るプログラム(mentatとccx両方)†
&link(kakutou.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/kakutou.f90)
雪平鍋の模様の半円筒を作るプログラム†
&link(yukihira.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/yukihira.f90)
雪平半円筒3Dプリンター用stlファイルを作るプログラム†
&link(yukihirastl.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/yukihirastl.f90)
ハニカム片持ち梁 上と下の板なしのモデルを作るプログラム(ccx s6要素)†
&link(hanikamu.f90,http://www.str.ce.akita-u.ac.jp/~gotouhan/takita/moderu/hanikamu.f90)
せん断補正係数の式 cowperとBankの比較†
グラフ†
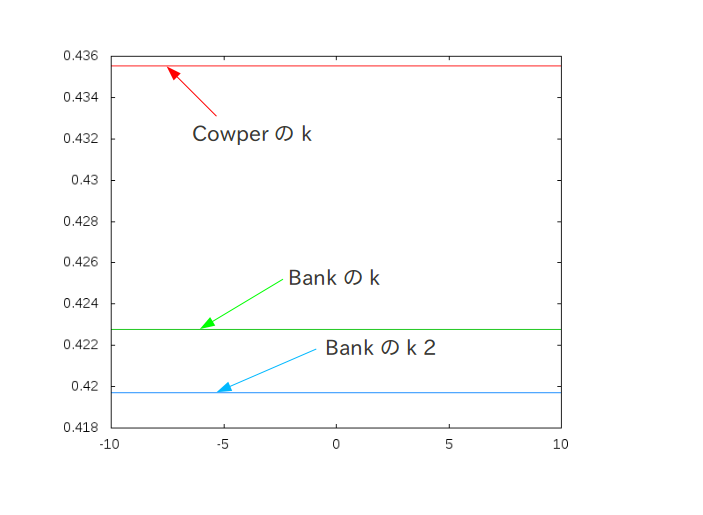
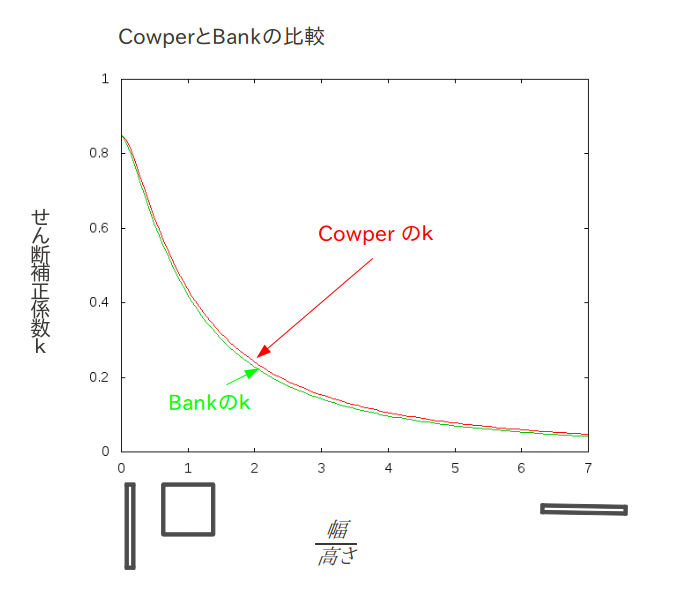
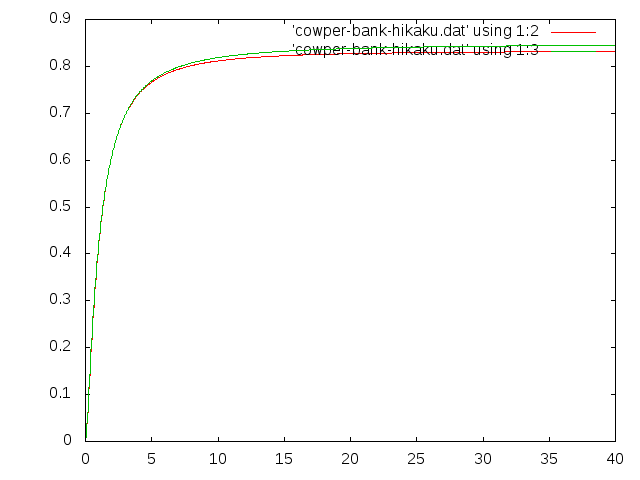
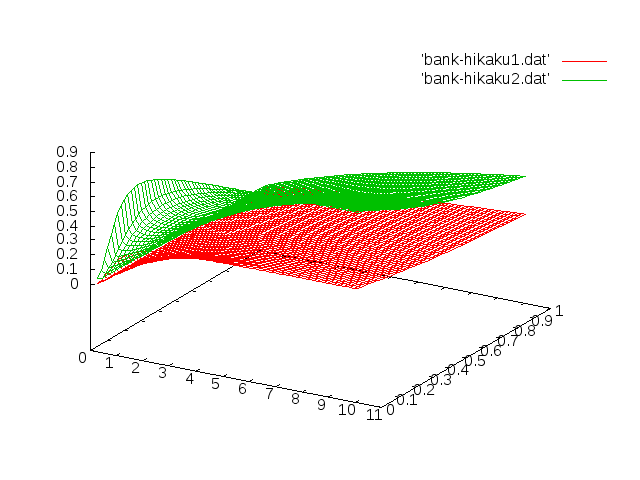
COWPERさんの式 論文名 The Shear Coefficient in Timoshenko's Beam Theory†
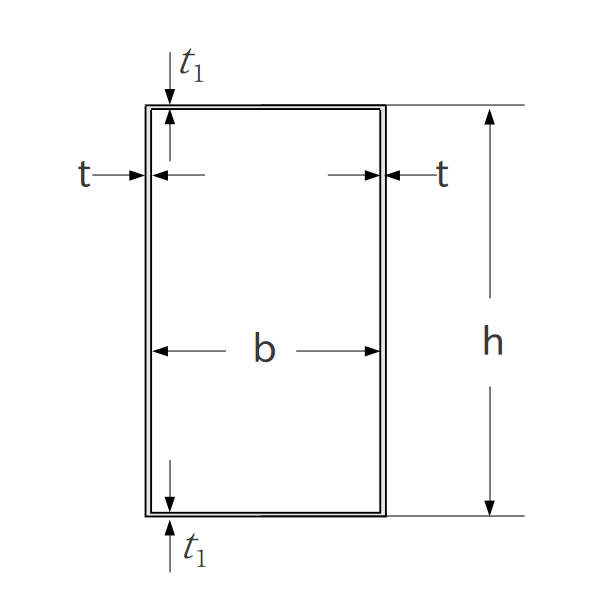
- 式
m=\( \frac{bt_1}{ht} \)
n=\( \frac{b}{h} \)
k=\( \frac{10(1+\nu)(1+3m)^2}{(12+72m+150m^2+90m^3)+\nu(11+66m+135m^2+90m^3)+10n^2((3+\nu)m+3m^2)} \)
Lawrence Bank さんの式 論文名 Shear Coefficients for Thin-Walled Composite Beams†
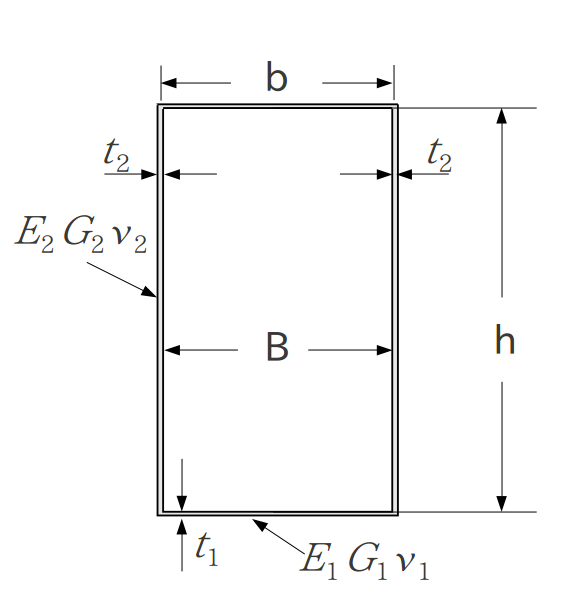
- 式
m=\( \frac{bt_1}{ht_2} \)
n=\( \frac{b}{h} \)
\( \alpha \)=\( \frac{E_2}{E_1} \)
\( k^{*} \)=\( \frac{20(\alpha+3m)^2}{\frac{E_1}{G_1}(60m^2n^2+60\alpha mn^2)+\frac{E_1}{G_2}(180m^3+300\alpha m^2+144\alpha^2 m+24\alpha^3)+\nu_1(-30m^2n^2-50\alpha mn^2)+\nu_2(30m^2+6\alpha m-4\alpha^2)} \)
\( k^*E_{z}A \)の値†
森吉立川モデル†
\( k^*EA \)=35102552
三種町モデル†
\( k^*EA \)=49217677
たわみ公式†
片持ち等分布†
- \( M_{(z)} \)=\( \frac{-qz^2}{2} \)+\( q \)\( \ell \)\( z \)-\( \frac{q\ell^2}{2} \)
- \( -EIv'' \)=\( \frac{-qz^2}{2} \)+\( q \)\( \ell \)\( z \)-\( \frac{q\ell^2}{2} \)
- \( -EIv' \)=\( \frac{-qz^3}{6} \)+\( \frac{q\ell z^2}{2} \)-\( \frac{q\ell^2z}{2} \)+A
- \( -EIv \)=\( \frac{-qz^4}{24} \)+\( \frac{q\ell z^3}{6} \)-\( \frac{q\ell^2z^2}{4}+A \)z+B
- 境界条件z=0でv=0よりB=0
- 境界条件z=0で\( \theta \)=0と\( \theta_{(z)} \)=\( \frac{M_{(z)}'}{kGA} \)-\( v' \)より
- \( \frac{A}{EI} \)=-\( \frac{ql}{kGA} \)
- \( v_{(z)} \)=\( \frac{1}{24EI} \)(\( qz^4 \)-\( 4q\ell z^3 \)+\( 6q\ell^2z^2 \))+\( \frac{q\ell z}{kGA} \)
- z=\( \ell \)のとき
たわみ=\( \frac{q\ell^4}{8EI} \)+\( \frac{q\ell^2}{kGA} \)
片持ち集中†
- \( v_{(z)} \)=\( \frac{P}{6EI} \)(3\( \ell \)\( z^2 \)-\( z^3 \))+\( \frac{P}{kGA} \)\( z \)
たわみ=\( \frac{P\ell^3}{3EI} \)+\( \frac{P\ell}{kGA} \)
単純支持集中†
- \( v_{(z)} \)=\( \frac{P}{48EI} \)(3\( \ell^2 \)\( z \)-\( 4z^3 \))+\( \frac{P}{2kGA} \)\( z \)(0\( \leqq \)\( z \)\( \leqq \)\( \frac{\ell}{2} \))
- z=\( \frac{\ell}{2} \)のとき
たわみ=\( \frac{p\ell^3}{48EI} \)+\( \frac{p\ell}{4kGA} \)
等曲げ スパン=\( \ell \) 拘束点から荷重までの距離=a†
- 0<z<aの時
\( $M_{(z)}=Pz \)$
\( $-EIv''=Pz \)$
\( $-EIv'=\frac{PZ^2}{2}+A \)$
\( $-EIv=\frac{PZ^3}{6}+Az+B \)$
\( $v_{(0)}=0 より B=0 \)$
\( $-EIv=\frac{PZ^3}{6}+Az \)$
\( $\theta_{(z)}=\frac{M'_{(z)}}{kGA}-v'_{(z)}=\frac{Pa}{kGA}-v'_{(z)} \)$
\( $\theta_{(a)}=\frac{Pa}{kGA}+\frac{1}{EI}(\frac{PZ^2}{2}+A) \)$
- a<z<\( \ell \)-aの時
\( $M_{(z)}=Pa \)$
\( $-EIv''=Pa \)$
\( $-EIv'=Paz+C \)$
\( $-EIv=\frac{Paz^2}{2}+Cz+D \)$
\( $v'_{(\frac{\ell}{2})}=0 より \)$
\( $0=\frac{Pa\ell}{2}+C \)$
\( $C=Paz-\frac{Pa\ell}{2} \)$
\( $-EIv'=Paz-\frac{Pa\ell}{2} \)$
\( $\theta_{(z)}=\frac{0}{kGA}+\frac{1}{EI}(Paz-\frac{Pa\ell}{2}) \)$
\( $\theta_{(a)}=\frac{1}{EI}(Pa^2-\frac{Pa\ell}{2}) \)$
- 連続なので
\( $\frac{Pa}{kGA}+\frac{1}{EI}(\frac{PZ^2}{2}+A)=\frac{1}{EI}(Pa^2-\frac{Pa\ell}{2}) \)$
\( $A=\frac{Pa^2}{2}-\frac{Pa\ell}{2}-\frac{PaEI}{kGA} \)$
\( $\frac{Pa^3}{6}+a(\frac{Pa^2}{2}-\frac{Pa\ell}{2}-\frac{PaEI}{kGA})=\frac{Paa^2}{2}+a(Paz-\frac{Pa\ell}{2})+D \)$
\( $D=\frac{Pa^3}{6}-\frac{PaEI}{kGA} \)$
- a<z<\( \ell \)-aの時
\( $-EIv=\frac{Paa^2}{2}+a(Paz-\frac{Pa\ell}{2})+\frac{Pa^3}{6}-\frac{PaEI}{kGA} \)$
\( $v=\frac{1}{EI}(-\frac{Pa}{2}z^2+\frac{Pa\ell}{2}z-\frac{Pa^3}{6})+\frac{Pa}{kGA} \)$
\( $v_{(\frac{\ell}{2})}=\frac{1}{EI}(-\frac{Pa^3}{8}+\frac{Pa^2\ell}{2}-\frac{Pa^3}{6})+\frac{Pa}{kGA} \)$
\( $v_{(\frac{\ell}{2})}=\frac{1}{EI}(\frac{Pa}{24}(3\ell^2-4a^2))+\frac{Pa}{kGA} \)$
\( $v_{(\frac{\ell}{2})}=\frac{Pa}{24EI}(3\ell^2-4a^2)+\frac{Pa}{kGA} \)$
salome†
- salomeでC3D4でメッシュを切れるやつ
Assign a set of hypotheses → 3D Automatic tetrahedralization(tetrahedron (netgen)
Netgen1D-2D-3D
cutとfuseの比較†
節点数などの比較†
| cut | cut | fuse | fuse |
| 節点数 | 要素数 | 節点数 | 要素数 |
| Netgen1D-2D-3D | 18038 | 74562 | 25113 | 102925 |
| tetrahedron(netgen) | 795 | 2815 | 661 | 2400 |
たわみ比較(最大を比較)†
| cut | fuse |
| Netgen1D-2D-3D | 5.5003E- | 5.5186E-3 |
| tetrahedron(netgen) | 4.6989E-3 | 4.7777E-3 |
メッシュ図†
3D Automatic tetrahedralization size25†

Netgen1D-2D-3D†

応急橋モデル(プログラムで組んだ)†
b=840mm h=450mm ell=5400mm
120 \( \times \) 120 \( \times \) 5400 の部材12
24 \( \times \) 450 \( \times \) 5400 の部材5
理論解 0.13336\( \sim \)0.13460 (I型)0.11917\( \sim \)0.12051 (矩形)

木橋たわみ 要素分割の影響†
| n | nx=4 ny=45 nz | nx=4 ny=45 nz | n | nx=4 ny*15 nz=32 | nx=4 ny*15 nz=32 | nx ny=45 nz=32 | nx ny=45 nz=32 |
| n | たわみ | 誤差 | n | たわみ | 誤差 | たわみ | 誤差 |
| 2 | 4.1693E-2 | -65.4% | 1 | 1.1481E-1 | -4.72% | 1.1399E-1 | -5.40% |
| 4 | 7.9925E-2 | -33.7 | 2 | 1.1491E-1 | -4.63 | 1.1474E-1 | -4.76 |
| 8 | 1.0391E-1 | -13.8 | 3 | 1.1494E-1 | -4.61 | 1.1487E-1 | -4.69 |
| 16 | 1.1215E-1 | -6.93 | 4 | 1.1495E-1 | -4.60 | 1.1494E-1 | -4.61 |
| 32 | 1.1494E-1 | -4.61 | 5 | 1.1495E-1 | -4.60 | 1.1497E-1 | -4.59 |
| 64 | 1.1559E-1 | -4.07 | 6 | | | 1.1499E-1 | 4.57 |
| 128 | 1.1576E-1 | -3.93 | 7 | | | 1.1500E-1m | -4.56 |
木橋 せん断補正係数kの誤差 ccxと理論値の比較 理論値0.1950791984†
| n | nx=4 ny=45 nz | nx=4 ny=45 nz | n | nx=4 ny*15 nz=32 | nx=4 ny*15 nz=32 | nx ny=45 nz=32 | nx ny=45 nz=32 |
| n | せん断弾性補正係数 | 誤差 | n | せん断弾性補正係数 | 誤差 | せん断弾性補正係数 | 誤差 |
| 2 | -6.78797E-2 | -134% | 1 | 0.27074 | 38.9% | 0.286786 | 47.0% |
| 4 | -0.19617 | -200% | 2 | 0.26890 | 37.8% | 0.272041 | 39.5% |
| 8 | 1.056237 | 441% | 3 | 0.26836 | 37.6% | 0.269637 | 38.2% |
| 16 | 0.330771 | 69.6% | 4 | 0.26818 | 37.5% | 0.268361 | 37.6% |
| 32 | 0.268361 | 37.6% | 5 | 0.26818 | 37.5% | 0.27818 | 37.3% |
| 64 | 0.257061 | 31.8% | 6 | | | 0.267457 | 37.1% |
| 128 | 0.254261 | 30.3% | 7 | | | 0.2672770 | 37.0% |
応急橋モデル2 ell=2.7 断面はモデル1と同じ†
木橋たわみ 要素分割の影響 荷重50KN†
| n | nx=4 ny=45 nz | nx=4 ny=45 nz | n | nx=4 ny*15 nz=32 | nx=4 ny*15 nz=32 | nx ny=45 nz=32 | nx ny=45 nz=32 |
| n | たわみ | 誤差 | n | たわみ | 誤差 | たわみ | 誤差 |
| 2 | 6.3400E-3 | | 1 | 1.0119E-2 | | 9.9231E-3 | |
| 4 | 8.7670E-3 | | 2 | 1.0143E-2 | | 1.0107E-2 | |
| 8 | 9.7468E-3 | | 3 | 1.0147E-2 | | 1.0135E-2 | |
| 16 | 1.0055E-2 | | 4 | 1.10147E-2 | | 1.0147E-2 | |
| 32 | 1.0147E-2 | | 5 | 1.10148E-2 | | 1.10152E-2 | |
| 64 | 1.0175E-2 | | 6 | | | 1.10154E-2 | |
| 128 | 1.0184E-2 | | 7 | | | 1.10156E-2 | |
| 256 | | | 8 | | | 1.0156E-2 | |
木橋 せん断補正係数kの誤差 ccxと理論値の比較†
| n | nx=4 ny=45 nz | nx=4 ny=45 nz | n | nx=4 ny*15 nz=32 | nx=4 ny*15 nz=32 | nx ny=45 nz=32 | nx ny=45 nz=32 |
| n | せん断弾性補正係数 | 誤差 | n | せん断弾性補正係数 | 誤差 | せん断弾性補正係数 | 誤差 |
| 2 | 12.33362 | | 1 | 0.25704 | | 0.27079 | |
| 4 | 0.39564 | | 2 | 0.25546 | | 0.25785 | |
| 8 | 0.28448 | | 3 | 0.25519 | | 0.25598 | |
| 16 | 0.261383 | | 4 | | | 0.25519 | |
| 32 | 0.25519 | | 5 | | | | |
| 64 | 0.25337 | | 6 | | | | |
| 128 | | | 7 | | | | |
| 256 | | | 8 | | | | |
応急橋モデル3 ell=2.5 E=5.69GPa G=\( \frac{E}{15} \)†
実験値と比較 荷重40.16KN(プログラムは半分で片持ちなので20.08KN)†
- 実験値 最低5.605mm 最大5.91mm 平均5.76383mm
- 実験値の結果から求めたせん断弾性補正係数k=
| 分割数 | プログラムたわみ | 誤差最低 | 誤差最大 | 誤差平均 | プログラムせん断弾性補正係数 | k誤差 |
| nx=4 ny=45 nz=2 | 3.648E-3 | 35.8 | -38.3 | -36.7 | 1.59695 | 559 |
| nz=4 | 4.9281E-3 | -13.2 | -16.7 | -14.5 | 0.36444 | 50.4 |
| nz=8 | 5.4329E-3 | -4.4 | -8.1 | -5.7 | 0.27940 | 15.3 |
| nz=16 | 5.5924E-3 | -1.5 | -5.4 | -3.6 | 0.26021 | 7.4 |
| nz=32 | 5.6402E-3 | -0.7 | -4.6 | -2.1 | 0.25496 | 5.2 |
| nz=64 | 5.6553E-3 | -0.4 | -4.3 | -1.9 | 0.25335 | 4.6 |
収束のグラフ†
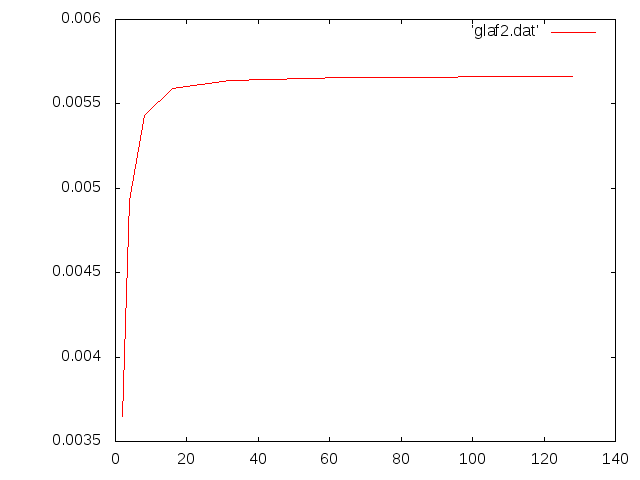
たわみ比較†
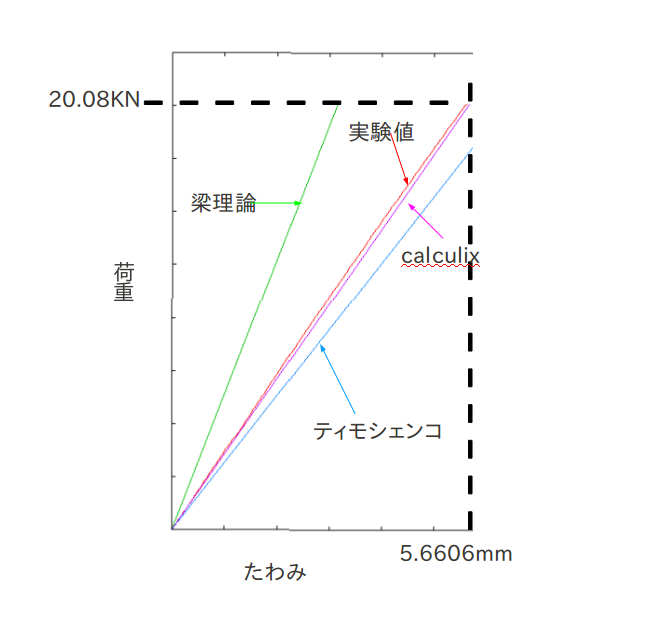
たわみと荷重比較†
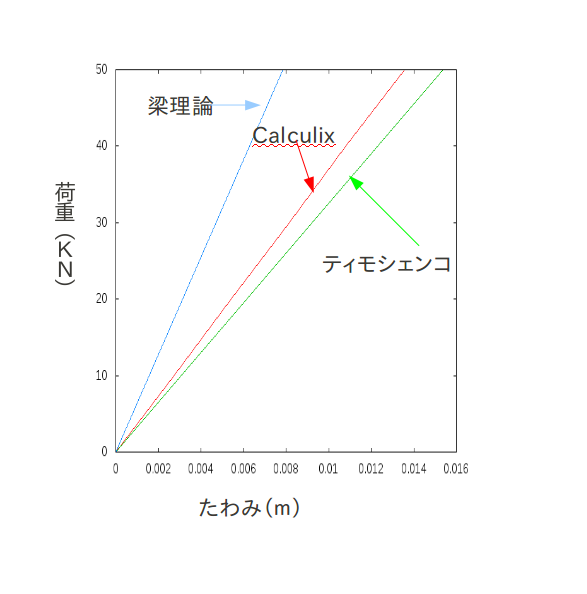
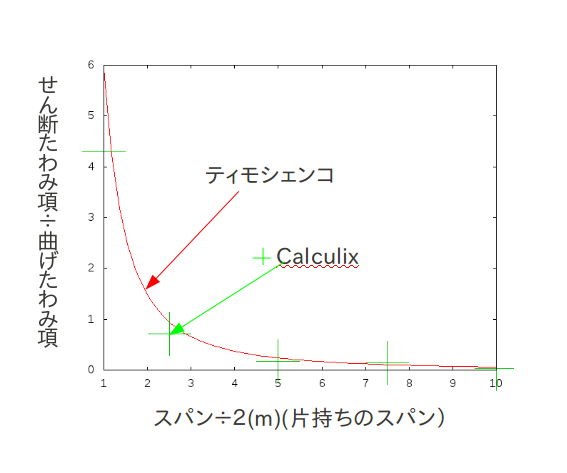
スパンとせん断の効き具合の比較†
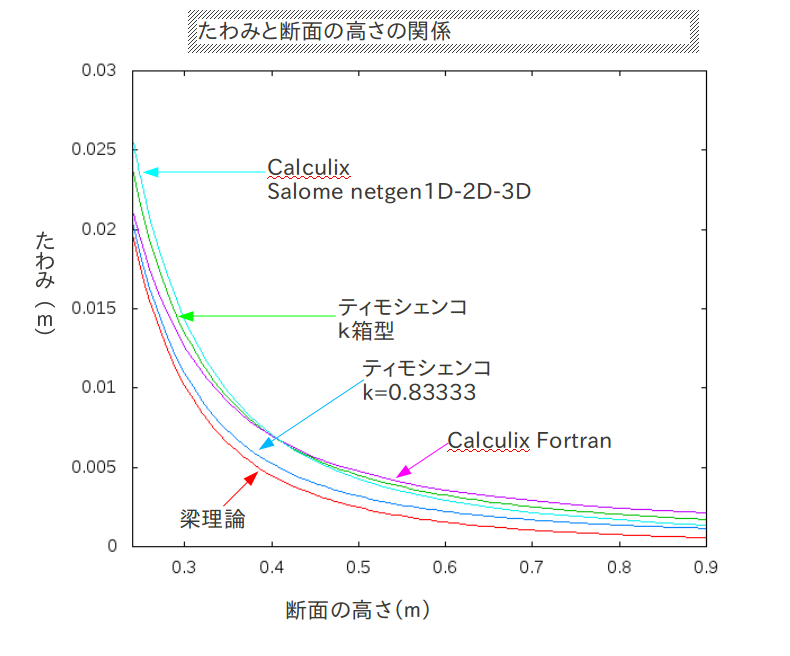
たわみと高さの関係のグラフ†
たわみと梁理論の比較と高さの関係のグラフ†
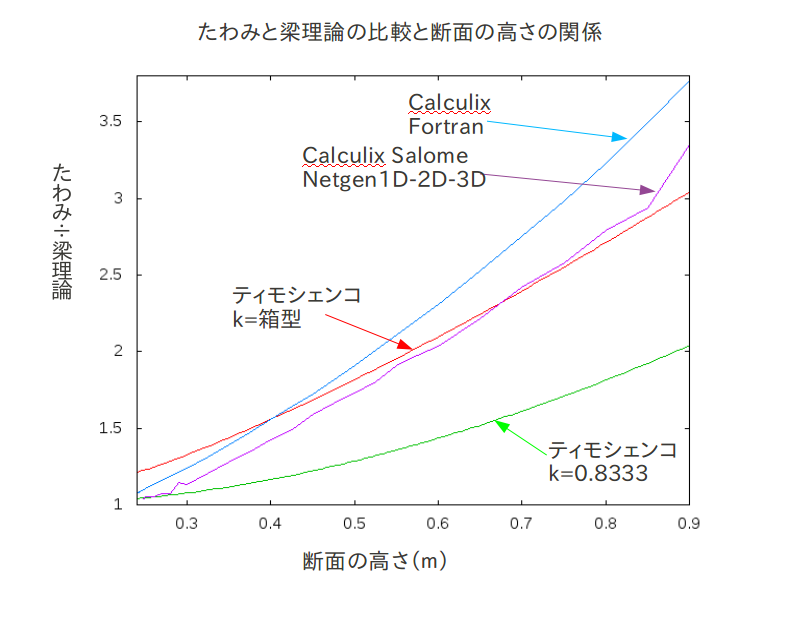
salomeとccxの比較†
オンサイト木橋 †
モデル図†
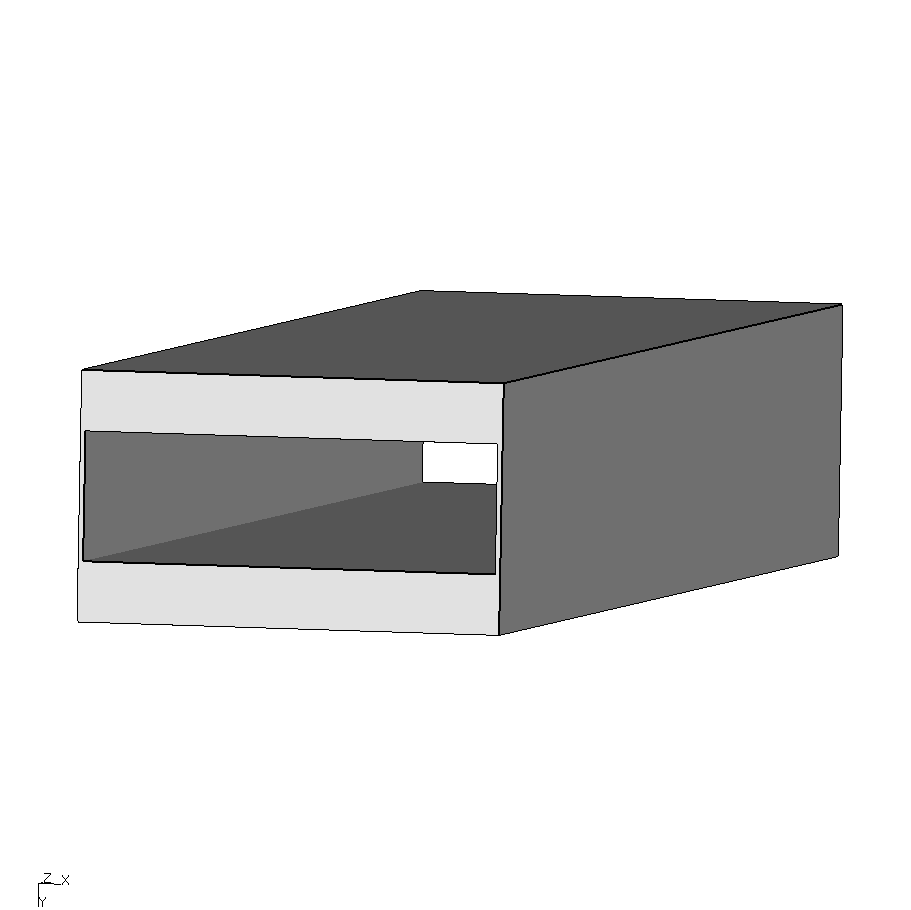
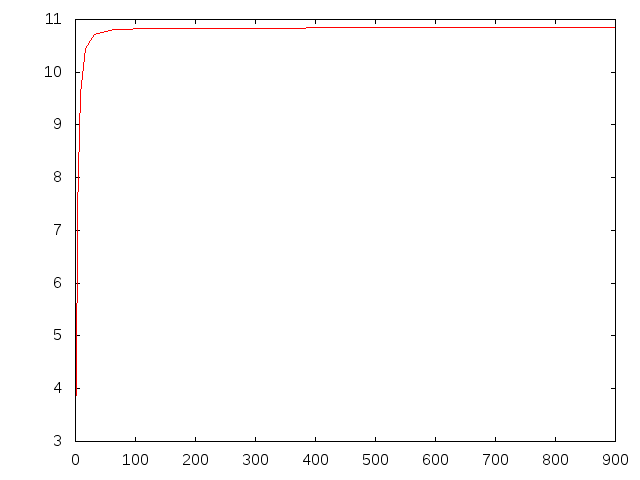
たわみ E=9GPa ell=3.0†
- nx=4 ny=25 nz
| n | たわみ | 誤差 | k | 誤差 |
| 2 | 3.8675E-3 | -62.6 | -9.148029 | -140.5 |
| 4 | 7.3529E-3 | -28.8 | -0.3778 | -267.5 |
| 8 | 9.6036E-3 | -7.0 | 0.3699 | 64.0 |
| 16 | 1.0459E-2 | 1.23 | 0.2111 | -6.3 |
| 32 | 1.0723E-2 | 3.78 | 0.1864 | -17.3 |
| 64 | 1.0803E-2 | 4.55 | 0.1800 | -20.1 |
| 128 | 1.0828E-2 | 4.80 | 0.1781 | -21.0 |
| 256 | 1.0836E-2 | 4.88 | 0.1775 | -21.2 |
| 512 | 1.0839E-2 | 4.90 | 0.1773 | -21.3 |
| 900 | 1.0840E-2 | 4.92 | 0.1772 | -21.4 |
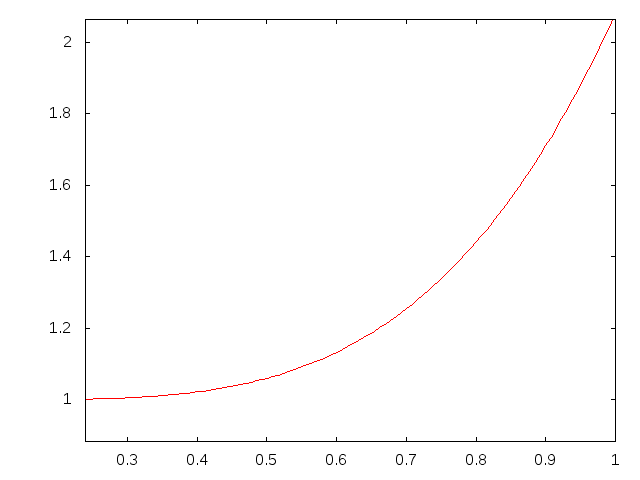
bankの理論値と梁理論との比較†
- \( k^* \)AEz
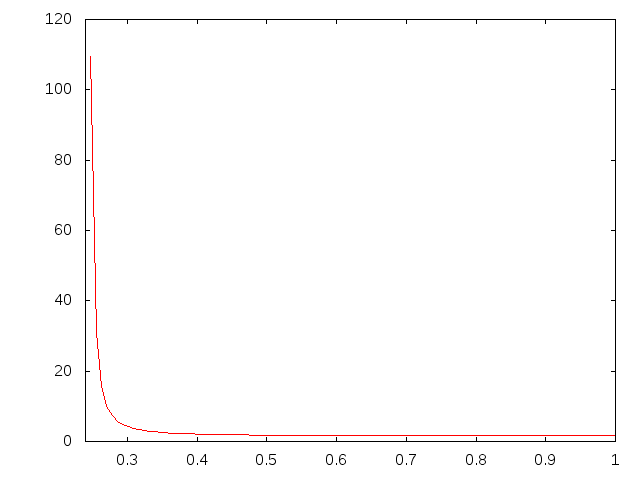
- \( k^* \)AE
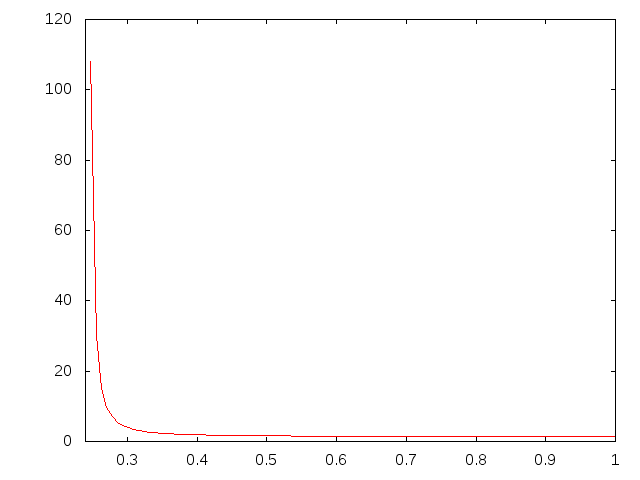
- \( k^* \)AEz 今までの鋼材と木材の式のなかでの関係を逆にしたもの
- \( k^* \)AE 今までの鋼材と木材の式のなかでの関係を逆にしたもの
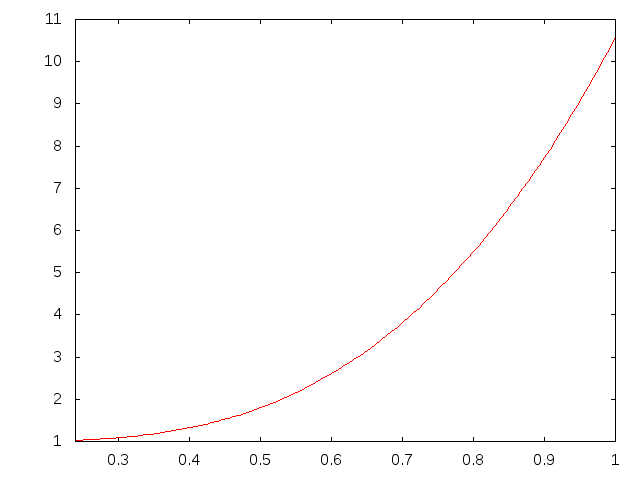
- \( k^* \)AE 今までの鋼材と木材の式のなかでの関係を逆にしたもの 全体の断面積\( \times \)鋼材のヤング率
たわみ収束グラフ†
link†
(加鳥さんの論文,ttps://www.jstage.jst.go.jp/article/kikaia1979/74/745/74_745_1220/_pdf)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)









