合板応急橋の試験データはk2のdata/gouhanの中
mentatエラー(終了番号の説明)†
http://www14.atwiki.jp/marc/pages/29.html
3300†
- 固有値抽出が最大許容反復回数内で収束できない。
- BUCKLEオプションで反復回数か収束判定許容差を大きくする。
3301†
- 質量か初期応力剛性がゼロになっている。
- 座屈解析では構造に荷重がすでに適用され、応力状態が存在していることを確認する。
3302†
- 解析においてランチョス法による固有値抽出の途中、非正定値マトリクスになった。
- 解析実行前に作用荷重を減らすか、BUCKLEを用いて逆べき乗法に切り替えてみる。
3305†
- BUCKLEオプションのTOLERANCEとMAX#をいじるといいかも
- あと次数にも影響してるっぽい
- BUCKLE MODESを3とかにしてみるとできたりする
mentat資料†
参考文献
mentatメモ†
mentatの起動の仕方†
mentat弾塑性解析†
- MATERIAL PROPERTES
- PLASTICITY→VON MISESS→ISOTROPIC→YEILD STRESS(初期降伏応力入力 N/mm2)
弾塑性モデルの作り方(鉄の引張)†
- 作成モデル

- 幅:0.1m,高さ0.1m,軸方向:1m
- ヤング率:206GPa
- 降伏点:235MPa
MESH GENERATION†
- NODES:ADD(x,y,z)座標を打ち込む
- (0,0,0) (1,0,0) (1,0.1,0) (0,0.1,0)
(0,0,0.1) (1,0,0.1) (1,0.1,0.1) (0,0.1,0.1)
- SUBDIVIDE(分割数)
- DIVISIONS(x,y,z)の順に分割数の値を入れる。
今回は分割数を(x:512,y:32,z:32)
- ELEMENTS→ALL:EXIST
MAIN MENUに戻る。
GEOMETRIC PROPERTIES(幾何学特性)†
- NEW→STRUCTURAL→3-D→SOLID→PROPERTIES→ASSUMED STRAIN
→OK→ELEMENTS:ADD→EXIST。
MAIN MENUに戻る。
MATERIAL PROPERTIES(材料特性)†
- MATERIAL PROPERTIES→NEW→STRUCTURAL→YONG'S MODULUS(ヤング率):206000(MPa),
POISSIN'S RATIO(ポアソン比):0.3を与える。
- 弾塑性要素にする場合
- PLASTICITY→YELD STRESS:235(MPa)→OK→ELEMENTS:ADD→EXIST。
MAIN MENUに戻る。
BOUNDARY CONDITIONS(境界条件)†
- NEW→STRUCTURAL→FIXED DISPLACEMENT→PROPERTIES
→DISPLACEMENT X Y Zにクリック。(X,Y,Zを拘束する)→OK
→NODES:ADD拘束したい箇所を囲む(点が緑になっていれば選択せれている)→右クリック。
- NEW→STRUCTURAL→POINT LOAD(荷重)またはFACE LOAD(面荷重)
- POINT LOAD(荷重)の場合
- FORCE X,Y,Zの与えたい方向を選択し、荷重を入力する。
- FACE LOAD(面荷重)の場合
- PRESSUREを選択し、与えたい応力(MN/m^2)を入力する。
→OK→FACES:ADD与えたい箇所を囲む→右クリック。
MAIN MENUに戻る
LOADCASES†
- NEW→STATIC→LOADS→すべての境界条件に必ずチェックを入れる。入れないと反映されない→STEPに1と入力
MAIN MENUに戻る
JOBS†
- NEW→PROPERTIES→lcase1をクリック。
→INITIAL LOAD→すべての境界条件に必ずチェックを入れる→OK
→JOB RESULTS(見たい結果にチェックを入れる)→今回はSTREESとTOTAL STRAINを選択→OK
→SAVE→RUN→SUBMIT(1)でモデルを走らせる
RESULTS(結果を見る)†
- どういう変形をしているか見たい時
- たわみの値を見たいとき
- SCALARをDisplacementX,Y,Zの見たい変位方向を選択し、OK→NUMERICS
- VIEWとかMOVEを駆使して節点番号を調べてから→Result→TOOLS→SHOW NODESで節点番号を入力するとその点のたわみ量が見れる。
降伏後の傾きの変え方†
- MATERIAL PROPERTIES→TABLES→NEW→1INDEPENDENT VARIABLE→TYPE:eq_plastic_strain→ADD(塑性ひずみ,応力)という感じで値を打ち込み、塑性後のグラフを作成する→FIT→RETURN→STRUCTURAL→PLASTICITY→YIELD STRESS1にする(降伏応力の設定table1をそのまま使用するため1倍とする)→TABLE→table1を選択→SHOW TABLEをSHOW MODELに直す
ccxからmentatにインポートする方法†
非一体化モデルの作り方†
インポート†
- FILE→INPORT→ABAQUS→モデルを選択(この時点では一体化モデル)
プレストレス(面荷重)†
- BOUNDARY CONDITION→NEW→STRUCTURAL→FACE LOAD→PROPERTIES→PRESSURE、ここに値を入力
- プレストレス値の決め方→本来、プレストレスの作用点は片持ち梁の場合、yz面から見れば上部に5箇所、下部に5箇所、裏にも同じようにあるので全部で20箇所ある。yz面から見た上部だけ考えると1箇所にかかるプレストレスは70kN=0.07MNで、これが5箇所あるので合計すると0.35MN。1要素にかかる力を1要素の面積で割ってあげると0.972MN/m2という値が得られる。
鋼板と木材をばらしてくっつける†
- とりあえず邪魔な矢印を一旦非表示にする、BOUNDARY CONDITIONで適当に境界条件を与える(後で必ず消す)→MESH GENERATION→MOVE→TRANSTLATIONSのxに適当な値を入れる→ELEMENT→離したい要素を選択→黄色になる→右クリック
※離れない場合 MESH GENERATION→SUBDIVIDE→DIVISIONS(1,1,1)で全てに適用でもう一度やってみる
- 全部やったらSWEEP→NODES→ALL
今の逆手順をやることで非一体の状態となる。TRANSTLATIONSのxにはマイナスをつける
- BOUNDARY CONDITION→プログラムの時点では1つの節点に付き0.000203252MN(断面の節点数246)となっているが、非一体化モデルでは一体化モデルより断面の節点が増えるので1つの節点に付き0.000146199MN(断面の節点数342)と与える
摩擦係数を与える†
- CONTACT→CONTACT BODIES→NEW→DEFORMABLE→PROPERTIES→FRICTION COEFFICIENT
→摩擦係数を入力→ELEMENT ADD→要素を選択→黄色になる→右クリック→現段階では要素に摩擦係数を与えている
LOADCASESの設定†
- LOADCASES→STATIC→LOADS→すべての境界条件に必ずチェックを入れる。入れないと反映されない→STEPに1と入力
JOBの設定†
- JOBS→PROPERTIES→INITIAL LOAD→すべての境界条件に必ずチェックを入れる
- JOBS→PROPERTIES→CONTACT CONTROL→TYPE→STICK SLIP
- JOBS→PROPERTIES→JOB RESULTS→STREESとTOTAL STRAINを選択
- JOBS→RUN
画面の配色†
- VISUALIZATION→COLORS→COLORMAPで番号を選択
要素が選択できない†
- VISUALIZATION→PLOT→RESET(下の方)してからREDRAW
節点や要素、境界条件の表示、非表示†
- VISUALIZATION→PLOT→それぞれのチェックを入れるか外す
ASSUMED STRAIN†
- GEOMETRIC PROPERTIES→PROPERTIES→ASSUMED STRAIN、ここにチェックを入れると今より正確な値が得られるかも?
結果を保存†
- モデルを走らせる→Result→open default→画面下のsave
- 結果を見たい時、走らせる前のモデルを開く→Result→open defaultの画面で保存した結果のファイルを開く
- 改めて結果を見たい時にわざわざ走らせなくていいので便利
たわみの値をみる†
- VIEWとかMOVEを駆使して節点番号を調べてから→Result→TOOLS→SHOW NODESで節点番号を入力する
グラフ†
書き方†
- Result→PATH PLOT→NODE PATH→2点選ぶ→選択した点が黄色になる→右クリック→ADD CURVE→ADD CURVE→VARIABLESで縦軸、横軸の順に項目を選択→FIT→完了
節点番号からたわみの値をみる†
- Result→TOOLS→SHOW NODE→節点番号を入力→下モニターにたわみの値が表示される
モデル画面への戻り方†
- PATH PLOTの画面でSHOW PATH PLOTをSHOW MODELにする
荷重が反映されない†
- インポートして境界条件で荷重以外の力(プレストレスとか)を入れた後にLOADCASESのLOADSにチェックを入れないと走らせた後に結果に反映されないので注意
dとE†
- mentatはEは読み込めるけど、dは読み込めないのでinpファイルなどに注意
mentat座屈解析†
- LOADCASESでいったんSTATICで解析した後にBUCKLEで再び解析するとできるみたい
- HELL要素で座屈荷重が得られなかったがJOBSでANALYSIS OPTIONSをいじったら手計算と同じ値が得られた。
倍率変更†
- DEFORMATION SCALINGをMANUALにして自分で値を入力する
鋼板を用いた弾塑性材料挟んだモデル†
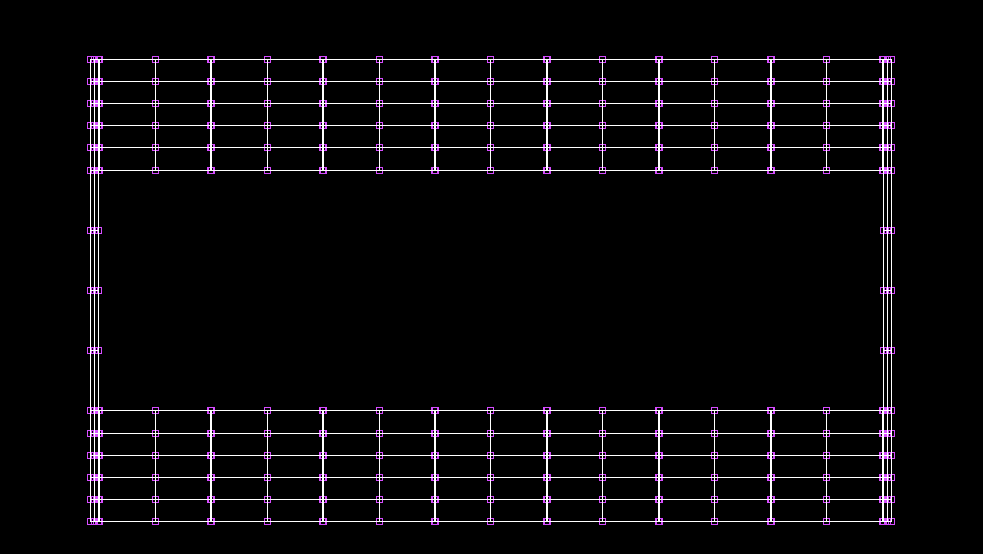
鋼板を用いた弾塑性要素モデル幅員方向とたわみ†
| 幅員方向(m) | 変位(mm) |
| 0 | 5.93122 |
| 0.0045 | 5.95046 |
| 0.009 | 5.96992 |
| 0.0095 | 5.99278 |
| 0.01 | 5.99186 |
| 0.07 | 6.33373 |
| 0.13 | 6.78022 |
| 0.1305 | 6.7855 |
| 0.131 | 6.78709 |
| 0.191 | 7.1762 |
| 0.251 | 7.53936 |
| 0.2515 | 7.54372 |
| 0.252 | 7.54454 |
| 0.312 | 7.77123 |
| 0.372 | 7.98269 |
| 0.3725 | 7.9854 |
| 0.373 | 7.98457 |
| 0.433 | 7.99928 |
| 0.493 | 7.98457 |
| 0.4935 | 7.9854 |
| 0.494 | 7.98269 |
| 0.554 | 7.77456 |
| 0.614 | 7.54454 |
| 0.6145 | 7.54372 |
| 0.675 | 7.53936 |
| 0.735 | 7.1462 |
| 0.7355 | 6.78709 |
| 0.736 | 6.7855 |
| 0.796 | 6.78022 |
| 0.856 | 6.33373 |
| 0.8565 | 5.99186 |
| 0.857 | 5.99278 |
| 0.8615 | 5.96992 |
| 0.866 | 5.95046 |
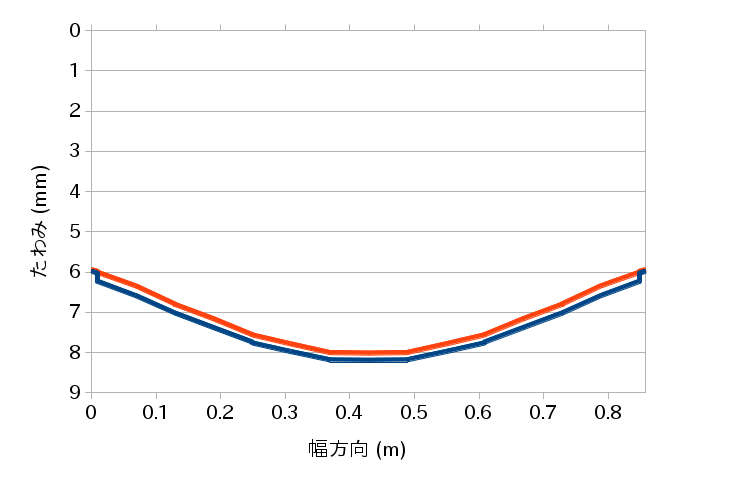
オンサイト木橋弾塑性材料挟んだモデルと非一体化モデルの比較†
- nz=512
- 縦軸:たわみ(m),横軸:幅方向(m)
- 赤線:弾塑性材料モデル,青線:非一体化モデル
弾塑性解析†
- せん断応力から降伏応力を求める式
\( \bar{\sigma}=\sqrt{3}\tau_{zx} \)
- 相当応力\( \bar{\sigma} \)を求める式
\( \bar{\sigma}=\sqrt{\frac{3}{2}}\sqrt{S_{xx}^2+S_{yy}^2+S_{zz}+2(S_{xy}^2+S_{yz}^2+S_{zx}^2)} \)
\( S_{xx}=\sigma_{xx}-\sigma_{m} \) \( S_{yy}=\sigma_{yy}-\sigma_{m} \) \( S_{zz}=\sigma_{zz}-\sigma_{m} \) \( S_{xy}=\sigma_{xy} \) \( S_{yz}=\sigma_{yz} \) \( S_{zx}=\sigma_{zx} \)
\( \sigma_{m}=\frac{1}{3}(\sigma_{xx}+\sigma_{yy}+\sigma_{zz}) \)
プレストレスを考慮する場合
\( \bar{\sigma}=\sqrt{\frac{3}{2}(\sigma_{zz}^2+2\sigma_{zx}^2)} \)
一番端に応力集中を防ぐために端の荷重をなくした場合†
真ん中の点(0.1m,0.04m,0.001m)†
| 荷重(N) | \( \sigma_{Mises} \) | 相当応力 | \( \sigma_{xx} \) | \( \sigma_{yy} \) | \( \sigma_{zz} \) | \( \tau_{xy} \) | \( \tau_{yz} \) | \( \tau_{zx} \) | 変位(m) |
| 1000 | 0.0860258 | 0.086016067 | 0 | 0 | 0 | 0 | 1.34224E-18 | 0.04966140 | 6.29E-10 |
| 5000 | 0.430129 | 0.430080339 | 0 | 5.18696E-15 | 8.10463E-17 | 0 | 0 | 0.248307 | 3.14584E-9 |
| 10000 | 0.860258 | 0.860160679 | 0 | 1.037E-14 | 1.620E-16 | 0 | 3.13985E-18 | 0.496614 | 6.29167E-9 |
| 15000 | 1.29039 | 1.29024102 | 0 | 0 | 1.29674E-15 | 0 | 2.148E-17 | 0.744921 | 9.4375E-9 |
| 20000 | 1.72052 | 1.720321359 | 0 | 0 | 0 | 0 | 1.514E-17 | 0.993228 | 1.25833E-8 |
| 25000 | 2.15064 | 2.150393039 | 8.299E-14 | 0 | 6.4837E-16 | 0 | 4.29518E-17 | 1.24153 | 1.573E-8 |
| 26000 | 2.23667 | 2.236424003 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.2912 | 1.63583E-8 |
| 29000 | 2.49475 | 2.494464932 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.44018 | 1.82458E-8 |
| 30000 | 2.58077 | 2.580478575 | 0 | 0 | 0 | 0 | 8.347E-17 | 1.48984 | 1.8875E-8 |
挟む部材に一様な荷重かけた場合†
- 降伏応力:100MPa
- 長さ:200mm=0.2m
- 幅:80mm=0.08m
- 高さ:1mm=0.001m
真ん中の点(0.1m,0.04m,0.001m)†
| 荷重(N) | \( \sigma_{Mises} \) | 相当応力 | \( \sigma_{xx} \) | \( \sigma_{yy} \) | \( \sigma_{zz} \) | \( \tau_{xy} \) | \( \tau_{yz} \) | \( \tau_{zx} \) | 変位(m) |
| 1000 | 0.0860258 | 0.086016067 | 0 | 0 | 0 | 0 | 1.34224E-18 | 0.04966140 | 6.29E-10 |
| 5000 | 0.430129 | 0.430080339 | 0 | 5.18696E-15 | 8.10463E-17 | 0 | 0 | 0.248307 | 3.14584E-9 |
| 10000 | 0.860258 | 0.860160679 | 0 | 1.037E-14 | 1.620E-16 | 0 | 3.13985E-18 | 0.496614 | 6.29167E-9 |
| 15000 | 1.29039 | 1.29024102 | 0 | 0 | 1.29674E-15 | 0 | 2.148E-17 | 0.744921 | 9.4375E-9 |
| 20000 | 1.72052 | 1.720321359 | 0 | 0 | 0 | 0 | 1.514E-17 | 0.993228 | 1.25833E-8 |
| 25000 | 2.15064 | 2.150393039 | 8.299E-14 | 0 | 6.4837E-16 | 0 | 4.29518E-17 | 1.24153 | 1.573E-8 |
| 26000 | 2.23667 | 2.236424003 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.2912 | 1.63583E-8 |
| 29000 | 2.49475 | 2.494464932 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.44018 | 1.82458E-8 |
| 30000 | 2.58077 | 2.580478575 | 0 | 0 | 0 | 0 | 8.347E-17 | 1.48984 | 1.8875E-8 |
- 荷重と変位(縦軸:荷重(N),横軸:変位(m))
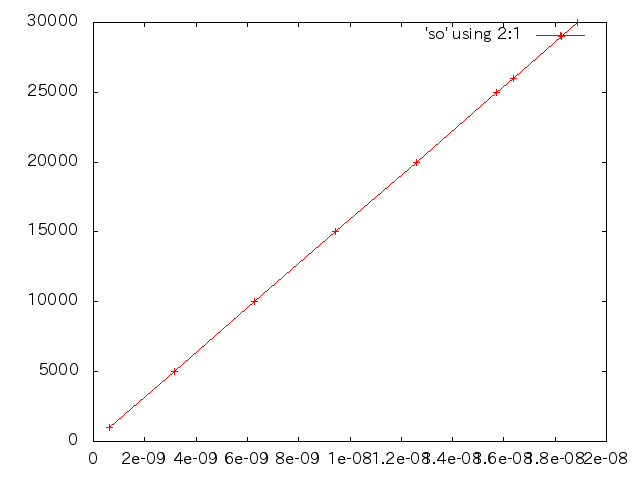
端の点(0.2m,0m,0.001m)†
- 応力が集中している
| 荷重(N) | \( \sigma_{Mises} \) | 相当応力 | \( \sigma_{xx} \) | \( \sigma_{yy} \) | \( \sigma_{zz} \) | \( \tau_{xy} \) | \( \tau_{yz} \) | \( \tau_{zx} \) | 変位(m) |
| 1000 | 0.701445 | 0.812 | 0.544447 | 0.085576 | -0.079059 | -0.0129 | 0.00276 | 0.255 | 5.232-9 |
| 10000 | 7.01445 | 8.066 | 5.44447 | 0.855756 | -0.79059 | -0.129121 | 0.0275558 | 2.54534 | 5.232E-8 |
| 15000 | 10.5217 | 12.18493247 | 8.1667 | 1.28363 | -1.18589 | -0.193681 | 0.0413337 | 3.818 | 7.84864E-8 |
| 20000 | 12.2935 | 14.74743448 | 9.96516 | 2.07722 | -1.06716 | -0.200825 | 0.0464743 | 4.48041 | 1.08583E-7 |
| 25000 | 11.1995 | 14.17433036 | 8.53547 | 3.6565 | -0.334745 | -0.034878 | 0.0211037 | 4.8786 | 1.75359E-7 |
| 30000 | 10 | | 4.51615 | 3.26422 | -1.53686 | -0.118612 | -0.00761243 | 4.95781 | 4.65926E-7 |
- 30kN超えると3002となる(正常に終了できない)。
- 荷重と変位(縦軸:荷重(N),横軸:変位(m))
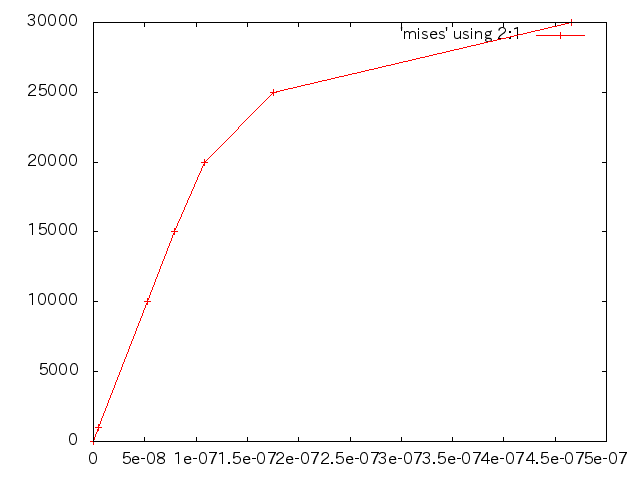
- mentatミーゼス応力の分布
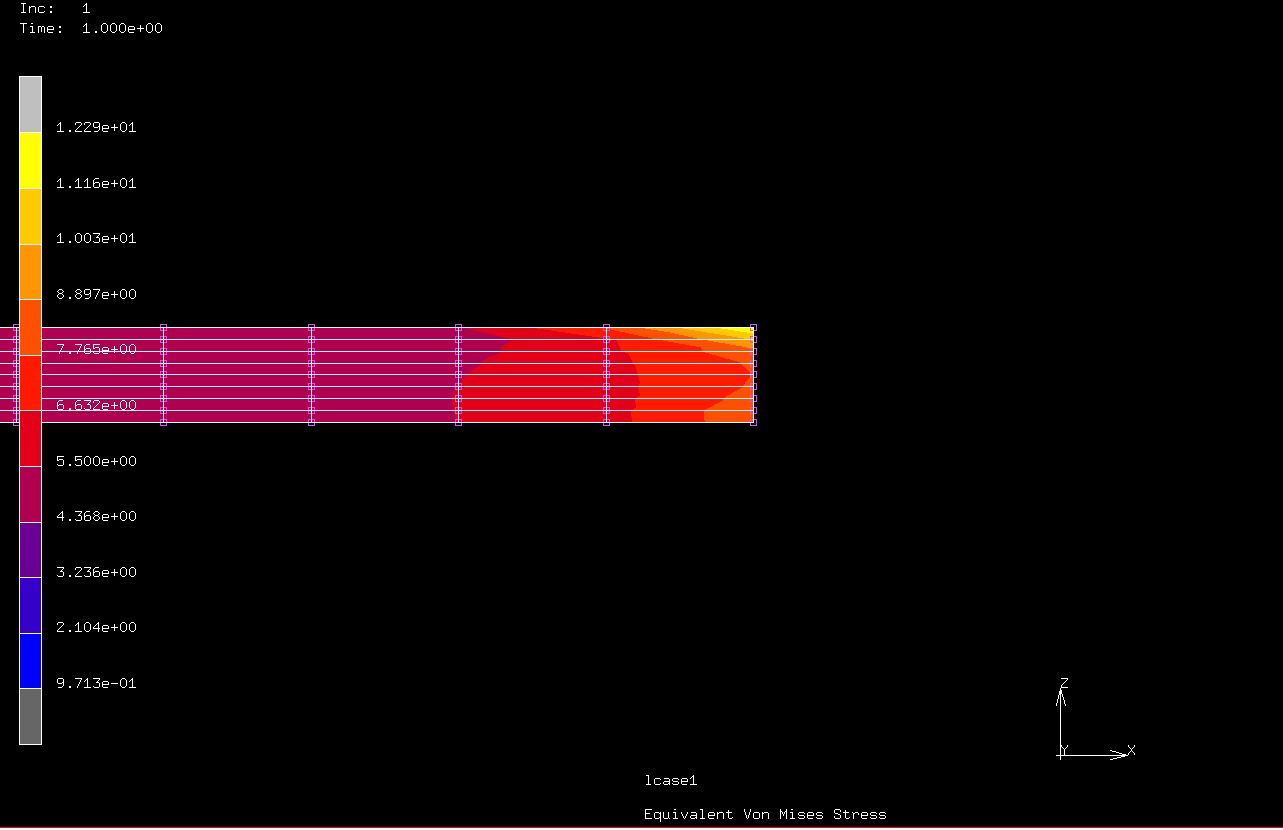
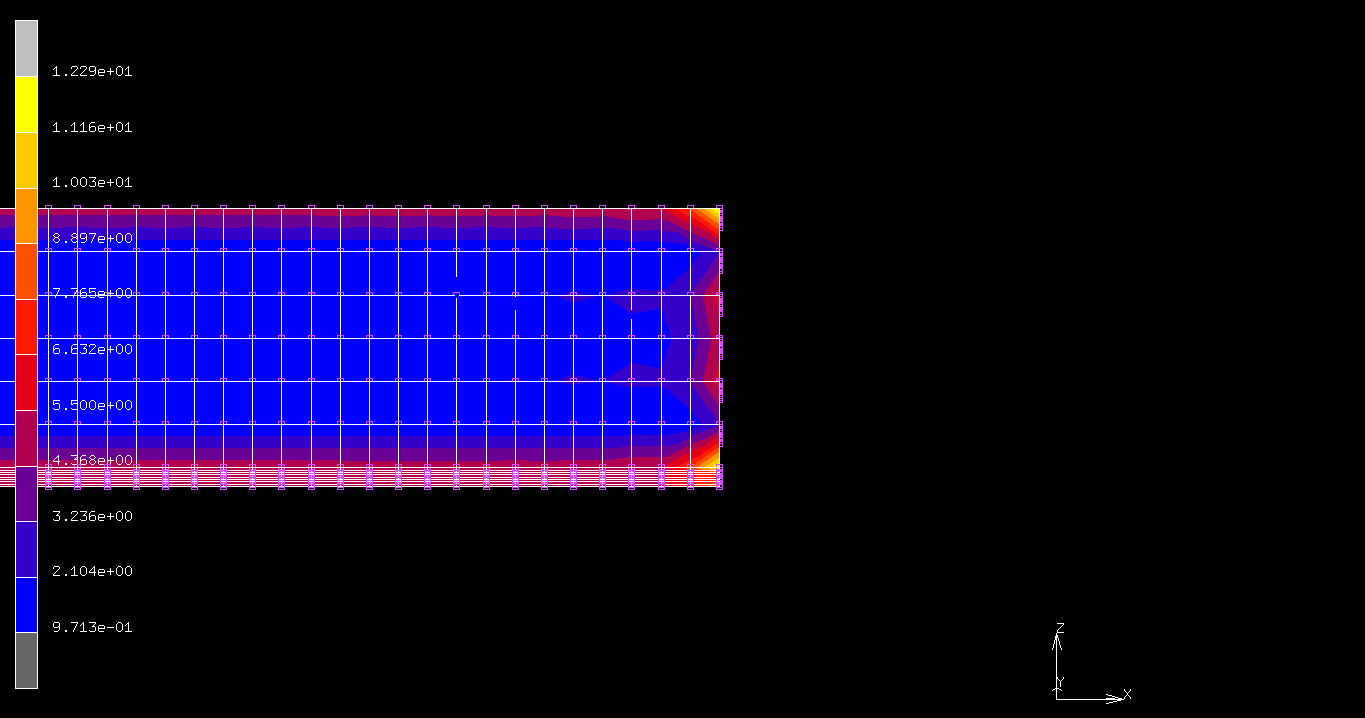
- 30kN載荷したとき
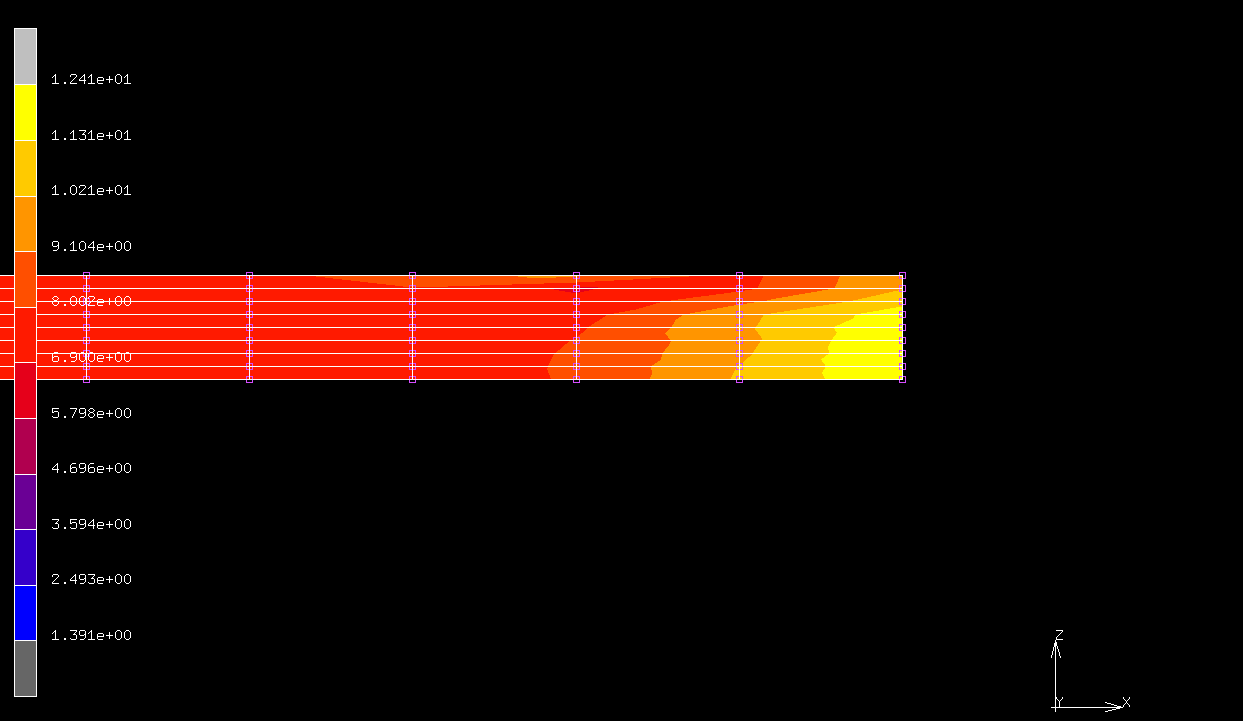
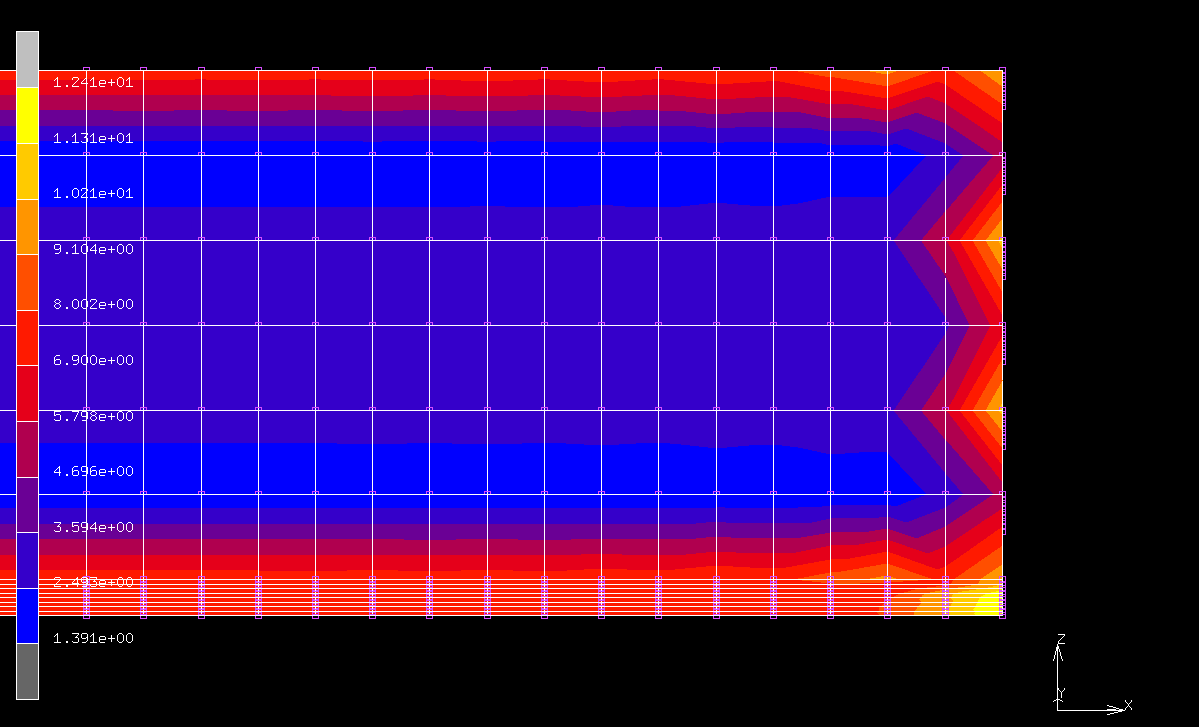
鋼板と挟む部材を組み合わせた場合†
| 荷重 | 変位(m) |
| 0 | 0 |
| 1000 | 5.23757E-6 |
| 5000 | 2.61878E-5 |
| 10000 | 5.23757E-5 |
| 20000 | 1.08686E-4 |
| 21000 | 1.18595E-4 |
| 22000 | 1.3037E-4 |
| 23000 | 1.42581E-4 |
| 24000 | 1.55667E-4 |
| 25000 | 1.7549E-4 |
| 30000 | 5.56882E-4 |
- 荷重と変位(縦軸:荷重(N),横軸:変位(m))
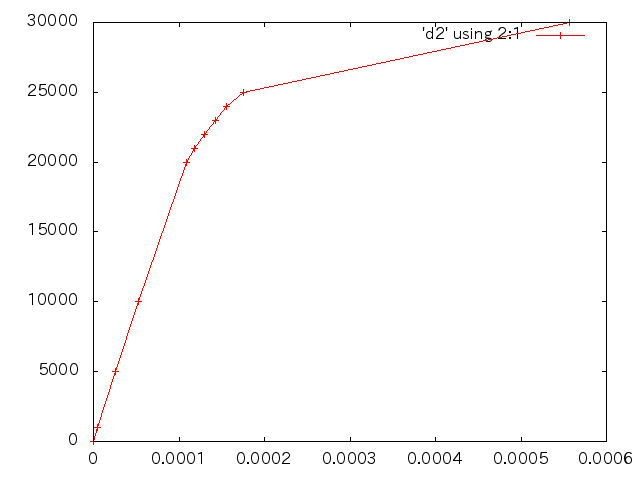
- 解析モデル
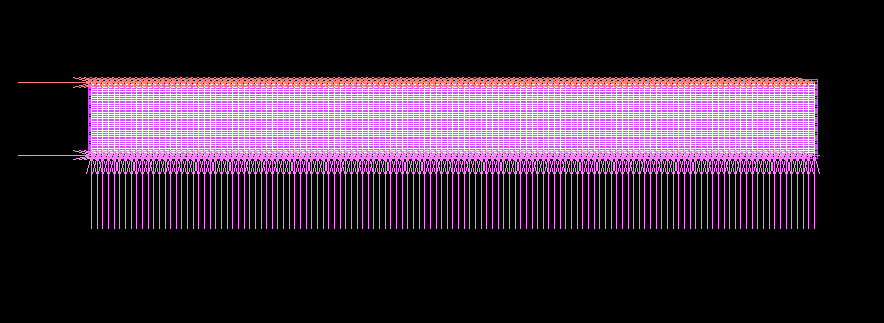
- 鉄の種類:SS400
- 降伏応力:235N/mm^2
- 鉄の寸法等
- 長さ:1m
- 幅:10cm
- 高さ:10cm
- ヤング率E=206GPa
- ポアソン比ν=0.3
- 断面積:100cm^2=10000mm^2
- 分割数:nx=128,ny=10,nz=10
| 荷重(N) | 変位(m) |
| 1.00E6 | 2.315E-5 |
| 2.00E6 | 4.630E-5 |
| 2.35E6 | 5.440E-5 |
| 2.50E6 | 5.787E-5 |
| 3.00E6 | 6.945E-5 |
| 4.00E6 | 9.260E-5 |
| 5.00E6 | 1.204E-4 |
| 6.00E6 | 1.569E-4 |
| 7.00E6 | 2.058E-4 |
| 8.00E6 | 3.079E-4 |
- 荷重と変位(縦軸:荷重(N),横軸:変位(m))
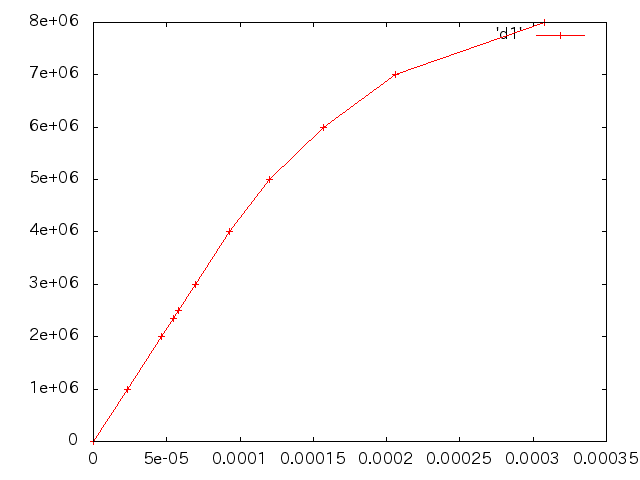
塑性論の基礎†
材料を挟んだ場合†
- 解析モデル
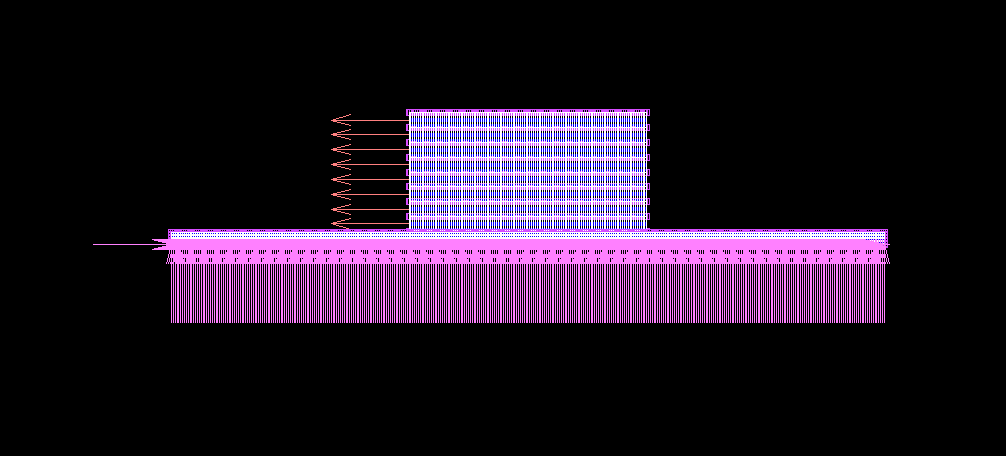
- 台(鋼材)の寸法等
- 分割数:nx=128,ny=6,nz=6
- 長さ:60cm
- 幅:24cm
- 高さ:1cm
- ヤング率:206GPa
- ポアソン比:0.3
- 試験体(木材)の寸法
- 分割数:nx=128,ny=6,nz=6
- 長さ:20cm
- 幅:8cm
- 高さ:10cm
- Ex=6GPa,Ey=Ex/25,Ez=Ex/25
- nxy=0.4,nyz=0.016,nzx=0.016
- Gxy=400,Gyz=400,Gzx=400
- 間に挟む材料の寸法等
- nx=128,ny=6,nz=2
- 長さ:20cm
- 幅:8cm
- 厚さ:1mm
- Ex=6GPa,Ey=Ex/25,Ez=Ex/25
- nxy=0.4,nyz=0.016,nzx=0.016
- Gxy=400,Gyz=400,Gzx=400
- 降伏応力:\( \sqrt{3} \)×摩擦試験のせん断降伏応力=1.0985E-04
| 引張力(N) | せん断応力σzx | 変位(m) |
| 0.5 | 1.992E-11 | 3.220E-5 |
| 0.6 | 2.392E-11 | 3.866E-5 |
| 0.7 | 2.794E-10 | 4.518E-5 |
| 0.8 | 3.209E-10 | 5.182E-5 |
- 引張力0.9でexit number3002解析できなくなる
- 分割数少なくすると解析できるそうだ
- 挟んだ材料に降伏条件を与えてもうまく降伏してくれない
接触解析†
- 解析モデル
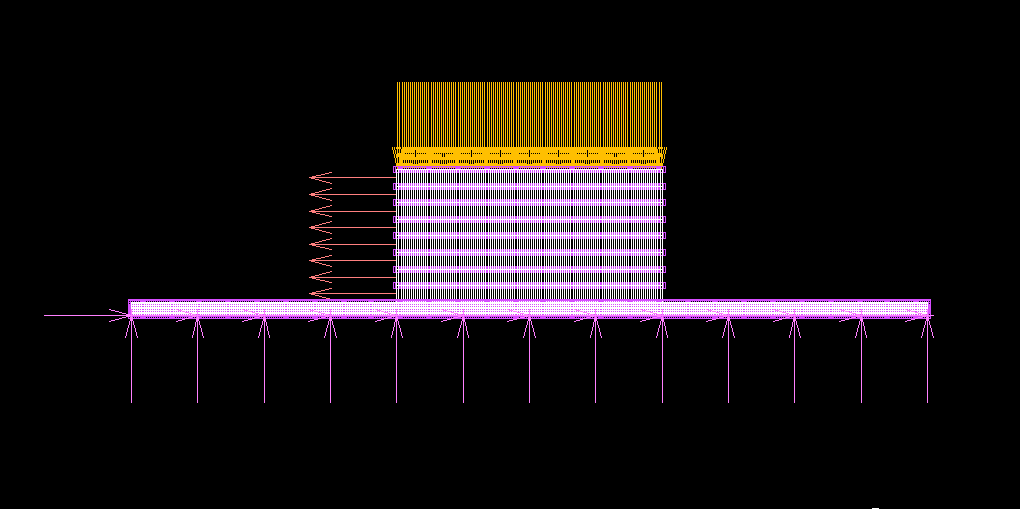
- 台(鋼材)の寸法等
- 長さ:60cm
- 幅:24cm
- 高さ:1cm
- ヤング率:206GPa
- ポアソン比:0.3
- 試験体(木材)の寸法
- 長さ:20cm
- 幅:8cm
- 高さ:10cm
- Ex=6GPa,Ey=Ex/25,Ez=Ex/25
- nxy=0.4,nyz=0.016,nzx=0.016
- Gxy=400,Gyz=400,Gzx=400
| 応力(MPa) | 変位(m) | 鋼材と木材のズレ(m) | せん断応力σzx(MPa) |
| 0.5 | 1.577E-08 | 0 | 0.256 |
| 0.6 | 1.893E-08 | 0 | 0.307 |
| 0.7 | 2.208E-08 | 0 | 0.358 |
| 0.8 | 2.523E-08 | 0 | 0.409 |
| 0.9 | 2.839E-08 | 0 | 0.461 |
| 1.0 | 3.074E-06 | 3.044E-06 | 0.501 |
| 1.1 | 1.573E-05 | 1.570E-05 | 0.519 |
| 1.2 | 0.12519 | 0.12519 | 0.677 |
- 応力と変位の関係(縦軸:応力σ 横軸:変位(m))
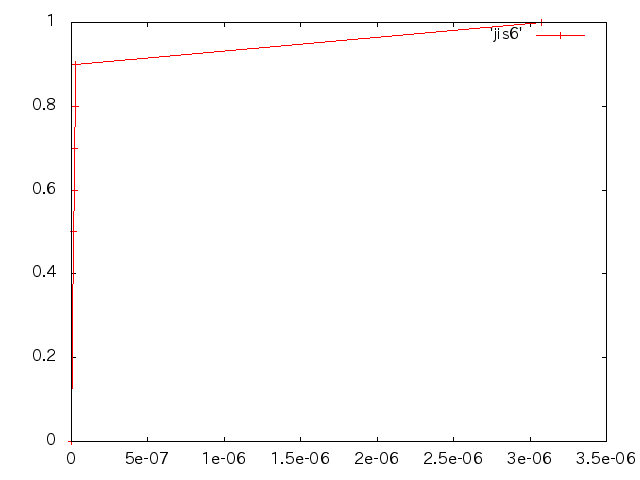
- 台(鋼材)の寸法等
- 長さ:60cm
- 幅:24cm
- 高さ:1cm
- ヤング率:206GPa
- ポアソン比:0.3
- 試験体(木材)の寸法
- 長さ:20cm
- 幅:8cm
- 高さ:10cm
- Ex=6GPa,Ey=Ex/25,Ez=Ex/25
- nxy=0.4,nyz=0.016,nzx=0.016
- Gxy=400,Gyz=400,Gzx=400
| 引張力(N) | 変位(m) | 鋼材と木材のズレ(m) | せん断応力σzx(MPa) |
| 0.5 | 1.971E-12 | 0 | 3.199E-05 |
| 0.6 | 2.366E-12 | 0 | 3.839E-05 |
| 0.7 | 2.760E-12 | 0 | 4.479E-05 |
| 0.8 | 3.154E-12 | 0 | 5.118E-05 |
| 0.9 | 3.549E-12 | 0 | 5.759E-05 |
| 0.99 | 3.909E-12 | 0 | 6.342E-05 |
| 1.0 | 2.484E-10 | 2.446E-10 | 6.328E-05 |
| 1.1 | 1.717E-09 | 1.713E-09 | 6.571E-05 |
- せん断応力と変位の関係(縦軸:せん断応力σzx 横軸:変位(m))
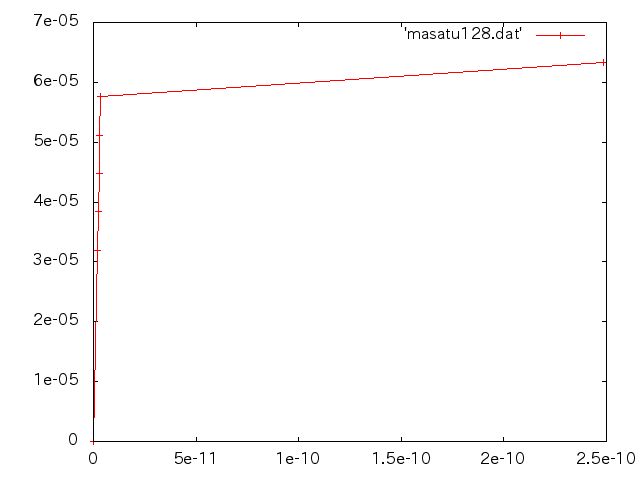
鉄の引張試験†
弾塑性解析†
- 解析モデル

- 鉄の種類:SS400
- 降伏応力:235N/mm^2
- 鉄の寸法等
- 長さ:1m
- 幅:10cm
- 高さ:10cm
- ヤング率E=206GPa
- ポアソン比ν=0.3
- 断面積:100cm^2=10000mm^2
- 分割数:nx=128,ny=10,nz=10
TABLEの場合†
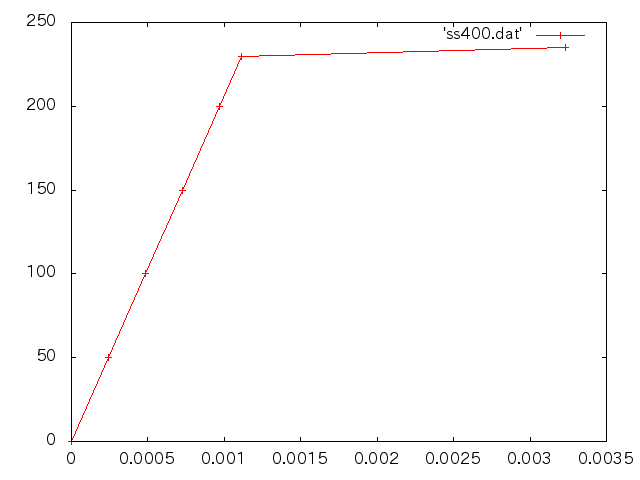
| 応力(MPa) | 伸び(m) | ひずみ | ヤング率(GPa) |
| 50 | 2.420E-4 | 2.420E-4 | 206.6 |
| 100 | 4.839E-4 | 4.839E-4 | 206.7 |
| 150 | 7.259E-4 | 7.259E-4 | 206.6 |
| 200 | 9.681E-4 | 9.681E-4 | 206.6 |
| 230 | 1.114E-3 | 1.114E-3 | 206.5 |
| 235 | 3.234E-3 | 3.234E-3 | |
- 応力とひずみの関係(縦軸:応力 横軸:ひずみ)
power lawの場合†
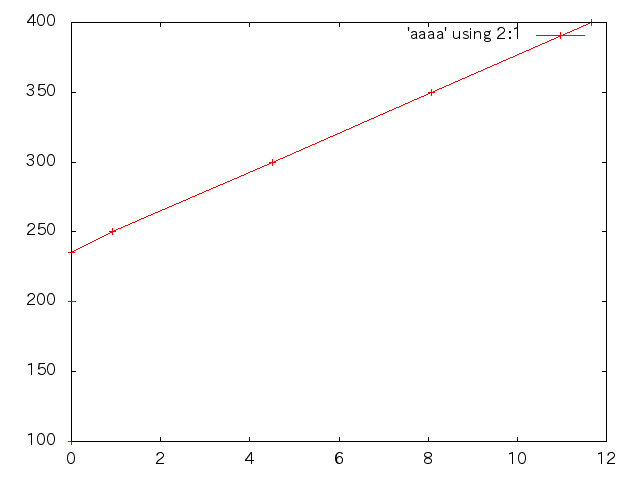
| 応力(MPa) | 伸び(m) | ひずみ | ヤング率(GPa) |
| 100 | 4.846E-4 | 4.839E-4 | 206.4 |
| 200 | 9.671E-4 | 9.671E-4 | 206.8 |
| 235 | 1.151E-3 | 1.151E-3 | 204.2 |
| 250 | 9.251E-1 | 9.251E-1 | |
| 300 | 4.502E-0 | 4.502E-0 | |
- 応力とひずみの関係(縦軸:応力 横軸:ひずみ)
TABLEを設定した場合†
- MATERIAL PROPATYの中にあるTABLE機能を用いて、応力と塑性ひずみを入力すれば、完全弾塑性体になる...?
- 傾きは自分で与える
- 与えた傾き、応力から塑性ひずみを逆算し、入力
- 弾性域の傾きは206000
- 塑性後の傾き2とした場合
- 与えた塑性ひずみ
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-2 |
| 235.2 | 1.005705E-1 |
| 235.3 | 1.505705E-1 |
| 235.4 | 2.005705E-1 |
| 235.5 | 2.505705E-1 |
- 解析結果
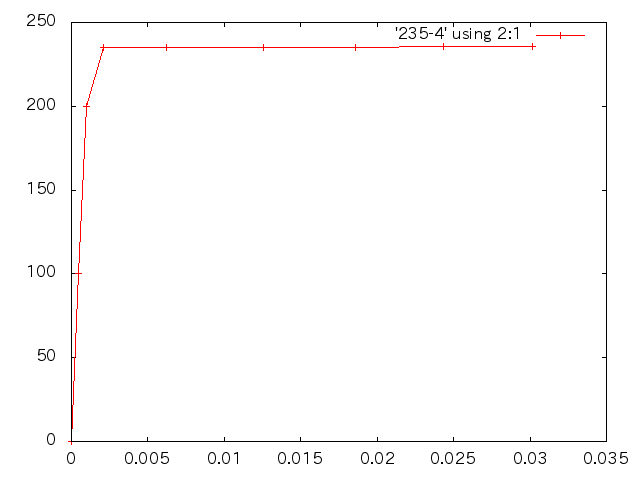
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 2.083E-3 | 2.083E-3 |
| 235.1 | 6.229E-3 | 6.229E-3 |
| 235.2 | 1.258E-2 | 1.258E-2 |
| 235.3 | 1.856E-2 | 1.856E-2 |
| 235.4 | 2.433E-2 | 2.433E-2 |
| 235.5 | 3.015E-2 | 3.015E-2 |
- 荷重と変位の関係(縦軸:荷重 横軸:ひずみ)
- 降伏後の傾き20とした場合
- 与えた塑性ひずみ
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-3 |
| 235.2 | 1.005705E-2 |
| 235.3 | 1.505705E-2 |
| 235.4 | 2.005705E-2 |
| 235.5 | 2.505705E-2 |
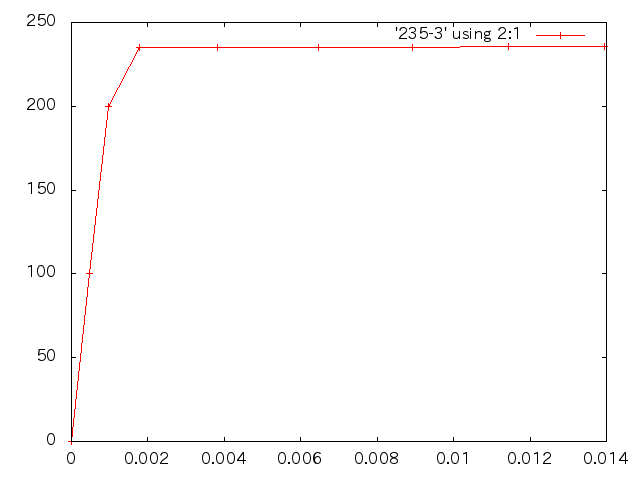
- 解析結果
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 1.316E-3 | 1.775E-3 |
| 235.1 | 3.829E-3 | 3.829E-3 |
| 235.2 | 6.453E-3 | 6.453E-3 |
| 235.3 | 8.930E-3 | 8.930E-3 |
| 235.4 | 1.143E-2 | 1.143E-2 |
| 235.5 | 1.394E-2 | 1.394E-2 |
- 荷重と変位の関係(縦軸:荷重 横軸:変位)
- 降伏後の傾き200とした場合
- 与えた塑性ひずみ
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-4 |
| 235.2 | 1.005705E-3 |
| 235.3 | 1.505705E-3 |
| 235.4 | 2.005705E-3 |
| 235.5 | 2.505705E-3 |
- 解析結果
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 1.316E-3 | 1.316E-3 |
| 235.1 | 1.738E-3 | 1.738E-3 |
| 235.2 | 2.119E-3 | 2.119E-3 |
| 235.3 | 2.508E-3 | 2.508E-3 |
| 235.4 | 2.902E-3 | 2.902E-3 |
| 235.5 | 3.298E-3 | 3.298E-3 |
- 応力と変位の関係(縦軸:応力 横軸:変位)
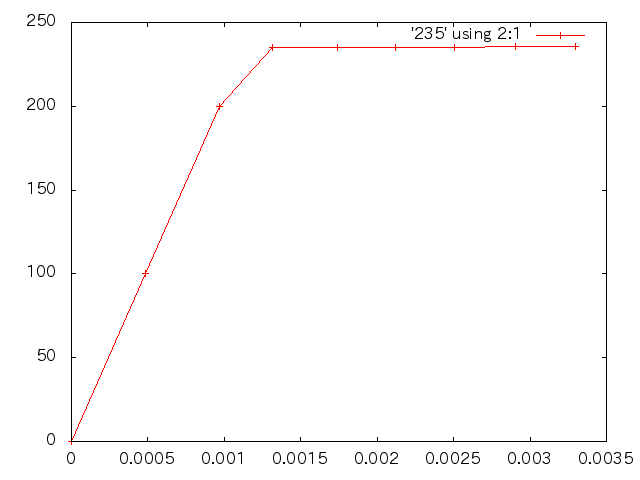
- 降伏後の傾き2000とした場合
- 与えた塑性ひずみ
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-5 |
| 235.2 | 1.005705E-4 |
| 235.3 | 1.505705E-4 |
| 235.4 | 2.005705E-4 |
| 235.5 | 2.505705E-4 |
- 解析結果
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.871E-4 |
| 235 | 1.183E-3 | 1.183E-3 |
| 235.1 | 1.225E-3 | 1.225E-3 |
| 235.2 | 1.270E-3 | 1.270E-3 |
| 235.3 | 1.315E-3 | 1.315E-3 |
| 235.4 | 1.361E-3 | 1.361E-3 |
| 235.5 | 1.406E-3 | 1.406E-3 |
- 応力とひずみの関係(縦軸:応力 横軸:ひずみ)
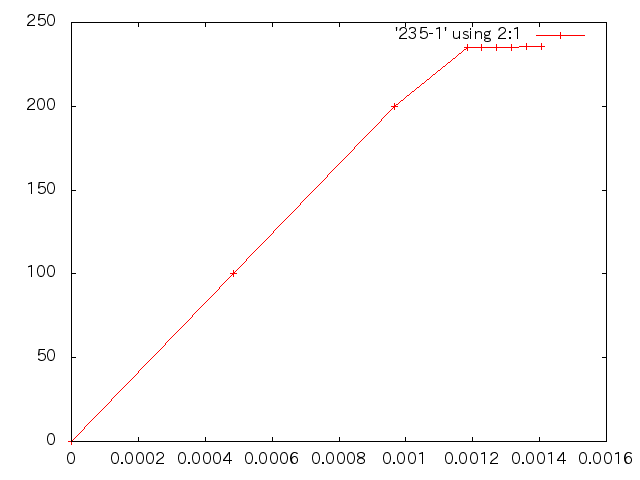
- 降伏後の傾き20000とした場合
- 与えた塑性ひずみ
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-6 |
| 235.2 | 1.005705E-5 |
| 235.3 | 1.505705E-5 |
| 235.4 | 2.005705E-5 |
| 235.5 | 2.505705E-5 |
- 解析結果
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 1.151E-3 | 1.151E-3 |
| 235.1 | 1.150E-3 | 1.150E-3 |
| 235.2 | 1.155E-3 | 1.155E-3 |
| 235.3 | 1.160E-3 | 1.160E-3 |
| 235.4 | 1.170E-3 | 1.170E-3 |
| 235.5 | 1.170E-3 | 1.170E-3 |
- 応力とひずみの関係(縦軸:応力 横軸:ひずみ)
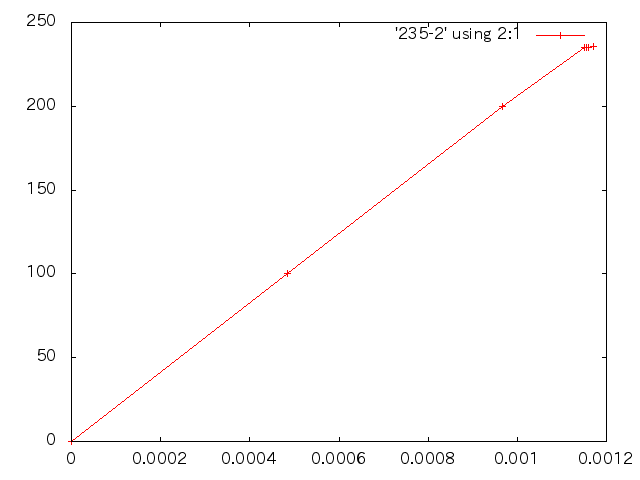
- 鋼材の弾塑性解析引張
鋼材の降伏応力:400N/mm^2
鋼材の寸法
長さ:1m
断面積:正方形断面10cm×10cm=100cm^2=10000mm^2
ヤング率206GPA
yield stress 400
FACELOAD を400付近で変えてみる
長さ1mなので伸び=ひずみ
断面分割数nx=ny=12,軸方向分割数=100
| FACELOAD | 最大変位(m) | 逆算ヤング率(GPa) |
| 380 | 1.840e-3 |
| 390 | 1.893e-3 |
| 399 | 2.050e-3 |
| 399.9 | 2.329e-3 |
| 400 | 5.732e-3 |
| 401 | 不明 15分以上掛かりそう |
オンサイト木橋モデル†
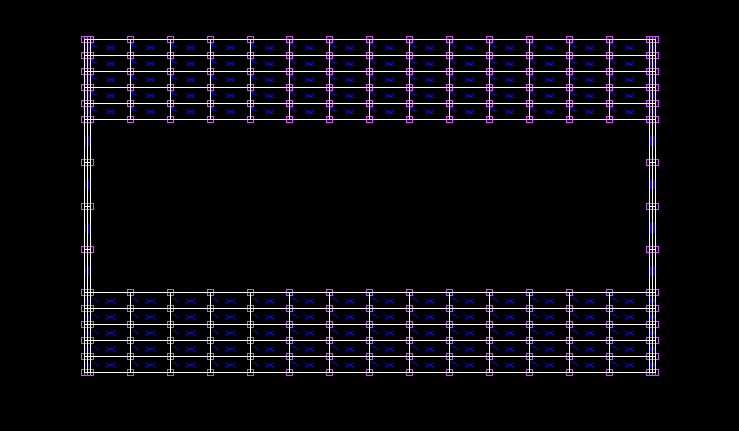
- 角材nx=2 , ny=5
- 鋼板nx=2 , ny=4
- Ezz木=6.921GPa , Exx木=Eyy木=Ezz木/25 , E鋼=206GPa
- νxy=0.4 , νyz=0.016 , νzx=0.016
- Gxy木=Gyz木=Gzx木=Ezz木/15 , G鋼=79GPa
後藤メモ†
鋼板のny=14では。
- 片持ち梁端部のたわみは、下端の値?
- Marc/Mentatで用いている直方体要素の名前は? mentatで要素を選ぶとき
応急橋モデル†
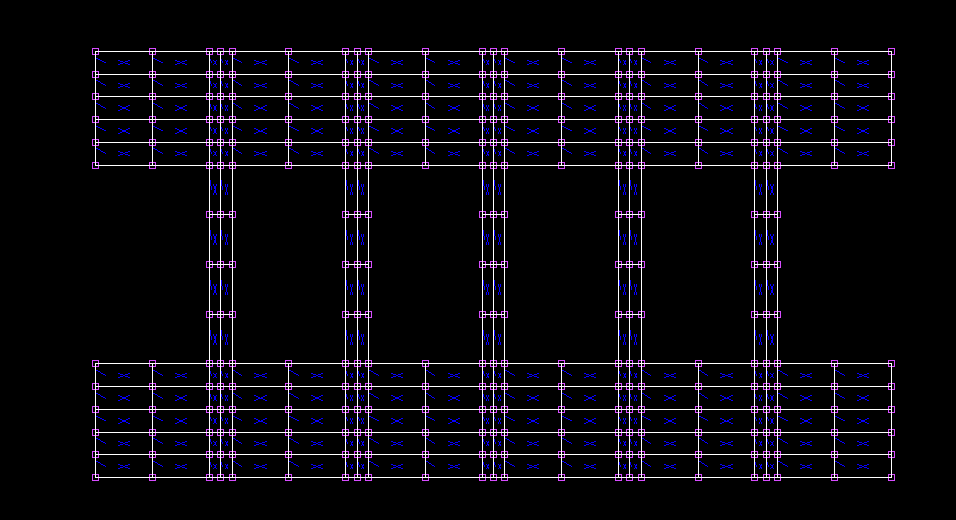
- 角材nx=2 , ny=5
- 合板nx=2 , ny=4
- Ezz木=5.690GPa , Exx木=Eyy木=Ezz木/25
- νxy=0.4 , νyz=0.016 , νzx=0.016
- Gxy木=Gyz木=Gzx木=Ezz木/15
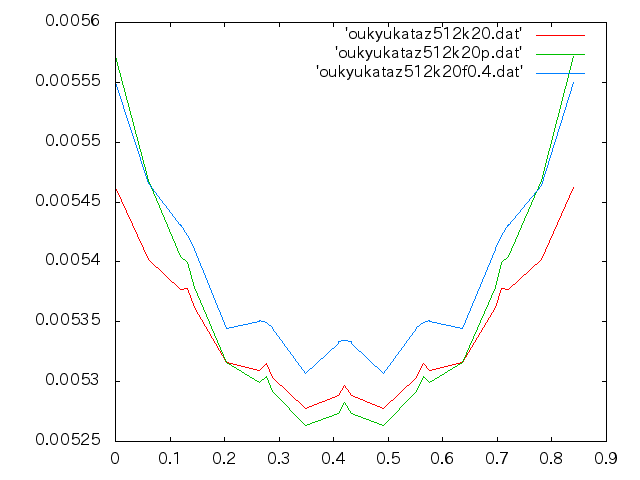
一体化モデルプレストレスありとなしと非一体化モデル摩擦係数0.4での比較†
- nz=512
- 縦軸:たわみ(m),横軸:幅方向(m)
- 赤線:一体化モデルプレストレスなし,緑線:一体化モデルプレストレスなし,青線:非一体化モデル摩擦係数0.4
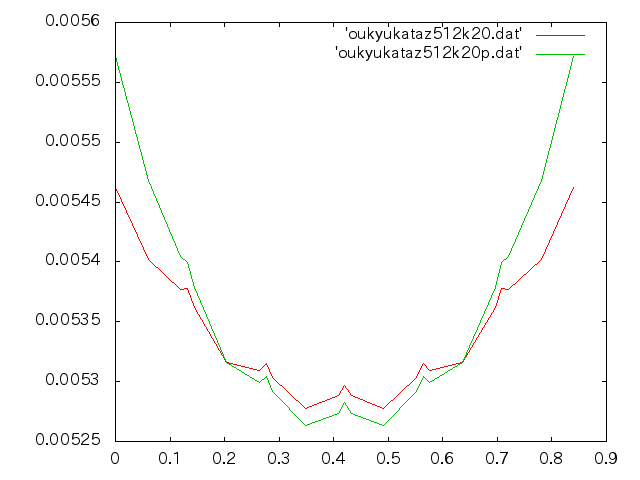
応急橋片持ち節点共有してないプレストレスあり…摩擦係数の変化で比較†
- nz=512
- 縦軸:たわみ(m),横軸:幅方向(m)
- 赤線:摩擦係数0.2,緑線:摩擦係数0.3,青線:摩擦係数0.4,紫線:摩擦係数0.5

応急橋片持ち節点共有・・・プレストレスなしとありの比較(mentat)†
- プレストレスなし節点共有①
| x(m) | 変位(m) |
| 0 | 5.46194E-03 |
| 0.06 | 5.40277E-03 |
| 0.12 | 5.37674-03 |
| 0.132 | 5.37784E-03 |
| 0.144 | 5.36153E-03 |
| 0.204 | 5.31605E-03 |
| 0.264 | 5.30943E-03 |
| 0.276 | 5.31517E-03 |
| 0.288 | 5.30314E-03 |
| 0.348 | 5.27756E-02 |
| 0.408 | 5.28814E-03 |
| 0.420 | 5.29707E-03 |
| 0.432 | 5.28814E-03 |
| 0.492 | 5.27756E-03 |
| 0.552 | 5.30314E-03 |
| 0.564 | 5.31517E-03 |
| 0.576 | 5.30943E-03 |
| 0.636 | 5.31605E-03 |
| 0.696 | 5.36153E-03 |
| 0.708 | 5.37784E-03 |
| 0.720 | 5.37674E-03 |
| 0.780 | 5.40227E-03 |
| 0.840 | 5.46194E-03 |
- プレストレスあり節点共有①
| x(m) | 変位(m) |
| 0 | 5.57192E-03 |
| 0.060 | 5.46803E-03 |
| 0.120 | 5.40478E-03 |
| 0.132 | 5.39994E-03 |
| 0.144 | 5.37865E-03 |
| 0.204 | 5.31558E-03 |
| 0.264 | 5.29956E-03 |
| 0.276 | 5.30416E-03 |
| 0.288 | 5.2914E-03 |
| 0.348 | 5.26369E-03 |
| 0.408 | 5.27337E-03 |
| 0.420 | 5.2822E-03 |
| 0.432 | 5.27337E-03 |
| 0.492 | 5.26369E-03 |
| 0.552 | 5.2914E-03 |
| 0.564 | 5.30416E-03 |
| 0.576 | 5.29956E-03 |
| 0.636 | 5.31558E-02 |
| 0.696 | 5.37865E-03 |
| 0.708 | 5.39994E-03 |
| 0.720 | 5.40478E-03 |
| 0.780 | 5.46803E-03 |
| 0.840 | 5.57192E-03 |
- 節点共有で固定・・・プレストレスなしとありの比較①
- 縦軸:たわみ(m),横軸:幅方向(m)
- 赤線:プレストレスなし,緑線:プレストレスあり
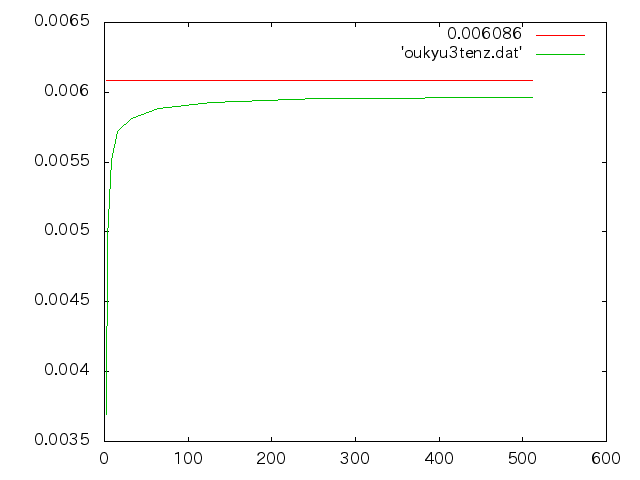
応急橋3点曲げ解析(mentat)†
- 荷重40KN
| 分割数(nz) | たわみ(m) | 相対誤差(%) |
| 2 | 3.693E-03 | 39.32 |
| 4 | 4.964E-02 | 18.44 |
| 8 | 5.511E-02 | 9.45 |
| 16 | 5.719E-02 | 6.03 |
| 32 | 5.816E-02 | 4.44 |
| 64 | 5.882E-02 | 3.35 |
| 128 | 5.930E-02 | 2.56 |
| 256 | 5.956E-02 | 2.14 |
| 512 | 5.965E-02 | 1.99 |
calculixとmentatの比較†
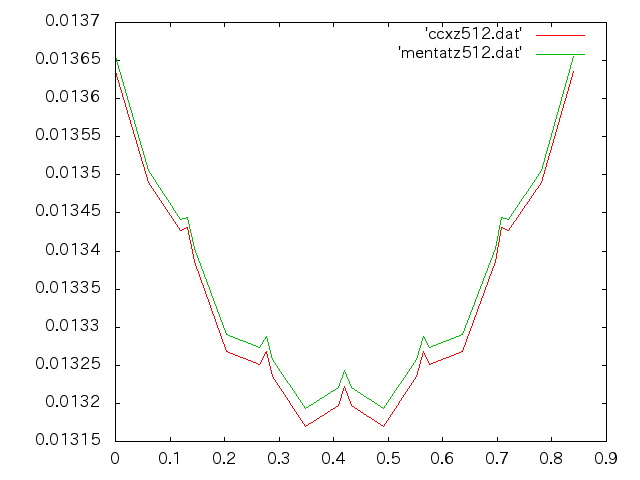
応急橋片持ち幅員方向とたわみの関係(nz=512)†
- 荷重50KN
| ccx | | mentat | |
| 幅方向x(m) | 変位(m) | 幅方向x(m) | 変位(m) |
| 0 | 1.363617E-02 | 0 | 1.36548E-02 |
| 0.06 | 1.35057E-02 | 0.06 | 1.35057E-02 |
| 0.12 | 1.34418E-02 | 0.12 | 1.34418E-02 |
| 0.132 | 1.34446E-02 | 0.132 | 1.34446E-02 |
| 0.144 | 1.34038E-02 | 0.144 | 1.34038E-02 |
| 0.204 | 1.32901E-02 | 0.204 | 1.32901E-02 |
| 0.264 | 1.32736E-02 | 0.264 | 1.32736E-02 |
| 0.276 | 1.32879E-02 | 0.276 | 1.32879E-02 |
| 0.288 | 1.32578E-02 | 0.288 | 1.32578E-02 |
| 0.348 | 1.31939E-02 | 0.348 | 1.31939E-02 |
| 0.408 | 1.32203E-02 | 0.408 | 1.32203E-02 |
| 0.420 | 1.32427E-02 | 0.420 | 1.32427E-02 |
| 0.432 | 1.32203E-02 | 0.432 | 1.32203E-02 |
| 0.492 | 1.31939E-02 | 0.492 | 1.31939E-02 |
| 0.552 | 1.32578E-02 | 0.552 | 1.32578E-02 |
| 0.564 | 1.32879E-02 | 0.564 | 1.32879E-02 |
| 0.576 | 1.32736E-02 | 0.576 | 1.32736E-02 |
| 0.636 | 1.32901E-02 | 0.636 | 1.32901E-02 |
| 0.696 | 1.34038E-02 | 0.696 | 1.34038E-02 |
| 0.708 | 1.34446E-02 | 0.708 | 1.34446E-02 |
| 0.720 | 1.34418E-02 | 0.720 | 1.34418E-02 |
| 0.780 | 1.35057E-02 | 0.780 | 1.35057E-02 |
| 0.840 | 1.36548E-02 | 0.840 | 1.36548E-02 |
- 縦軸:たわみ(m),横軸:幅方向(m)
- 赤線:ccx , 緑線:mentat
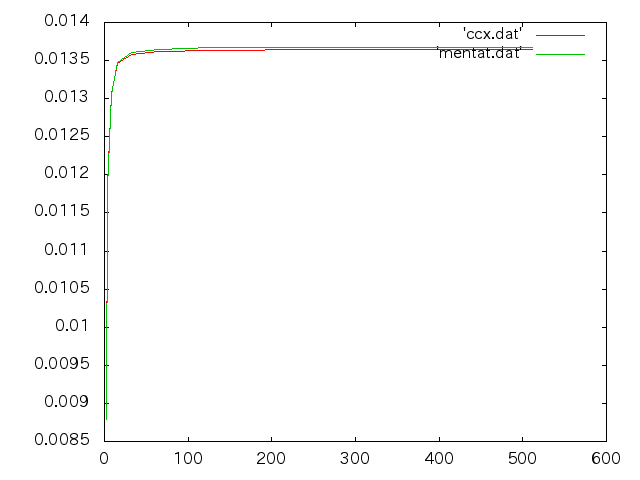
応急橋片持ちモデルnz†
- 荷重50KN
| 分割数 | calculix | | 分割数 | mentat | |
| nz | たわみ(m) | 相対誤差(%) | nz | たわみ(m) | 相対誤差(%) |
| 2 | 8.811E-03 | 42.09 | 2 | 8.786E-03 | 42.25 |
| 4 | 1.186E-02 | 22.05 | 4 | 1.183E-02 | 22.25 |
| 8 | 1.307E-02 | 14.10 | 8 | 1.306E-02 | 14.16 |
| 16 | 1.346E-02 | 11.53 | 16 | 1.347E-02 | 11.47 |
| 32 | 1.358E-02 | 10.75 | 32 | 1.360E-02 | 10.61 |
| 64 | 1.362E-02 | 10.48 | 64 | 1.365E-02 | 10.29 |
| 128 | 1.363E-02 | 10.42 | 128 | 1.367E-02 | 10.15 |
| 256 | 1.364E-02 | 10.35 | 256 | 1.367E-02 | 10.15 |
| 512 | 1.365E-02 | 10.29 | 512 | 1.367E-02 | 10.15 |
- 縦軸:たわみ(m),横軸:分割数
- 赤線:ccx , 緑線:mentat
calculix user manual 2.5†
P256~†
- DLOAD
- このオプションは、分布荷重を指定することができる。これらは要素の面に圧力荷重と質量載荷(単位質量あたりの荷重)重力による遠心力によっていずれかが含まれています。
次のように表面載荷するための要素の面は(要素の節点番号はセクション3.1を参照してください)番号が付けられています。
- (
六面体要素の:
face 1: 1-2-3-4
face 2: 5-8-7-6
face 3: 1-5-6-2
face 4: 2-6-7-3
face 5: 3-7-8-4
face 6: 4-8-5-1
四面体要素の:
Face 1: 1-2-3
Face 2: 1-4-2
Face 3: 2-4-3
Face 4: 3-4-1
くさび形要素の:
Face 1: 1-2-3
Face 2: 4-5-6
Face 3: 1-2-5-4
Face 4: 2-3-6-5
Face 5: 3-1-4-6
四辺形平面応力、平面ひずみと軸対称要素の場合:
Face 1: 1-2
Face 2: 2-3
Face 3: 3-4
Face 4: 4-1
三角形平面応力、平面ひずみと軸対称要素の場合:
Face 1: 1-2
Face 2: 2-3
Face 3: 3-1
梁要素の場合:
Face 1: pressure in 1-direction
Face 2: pressure in 2-direction
- )
ただひとつの種類の荷重(シェル上の法線方向の圧力)があるので、シェル要素には面番号は必要ありません。
後藤ちゃちゃ(13/7/13)†
後藤ちゃちゃ(13/7/13)†
ccx箱型断面片持ち†
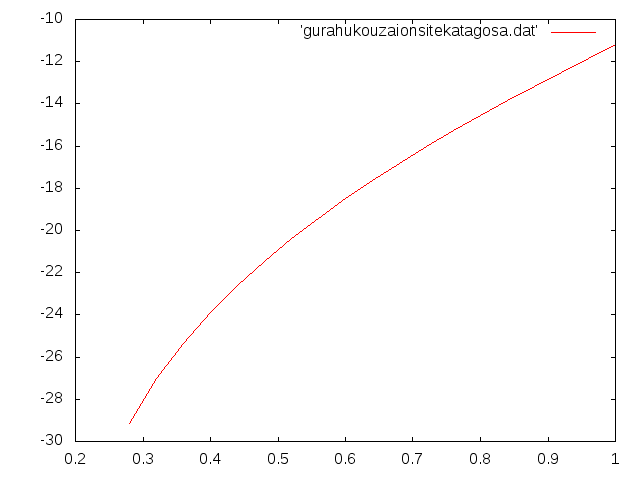
鋼材のみでオンサイト同寸法断面h2†
- b1=0.84m,b2=0.009m
- h1=0.12m,h2=0.24mから0.04m刻みで1.00mまで増加させた
- オンサイトのh2初期値=0.5m
- 厚さはオンサイトと同じ寸法
| h2(m) | 相対誤差(%) |
| 2.80000E-01 | -2.91321E+01 |
| 3.20000E-01 | -2.70221E+01 |
| 3.60000E-01 | -2.53371E+01 |
| 4.00000E-01 | -2.38924E+01 |
| 4.40000E-01 | -2.26134E+01 |
| 4.80000E-01 | -2.14579E+01 |
| 5.20000E-01 | -2.03999E+01 |
| 5.60000E-01 | -1.94169E+01 |
| 6.00000E-01 | -1.84997E+01 |
| 6.40000E-01 | -1.76312E+01 |
| 6.80000E-01 | -1.68089E+01 |
| 7.20000E-01 | -1.60234E+01 |
| 7.60000E-01 | -1.52692E+01 |
| 8.00000E-01 | -1.45412E+01 |
| 8.40000E-01 | -1.38387E+01 |
| 8.80000E-01 | -1.31560E+01 |
| 9.20000E-01 | -1.24906E+01 |
| 9.60000E-01 | -1.18417E+01 |
| 1.00000E+00 | -1.12070E+01 |
- 相対誤差と高さh2の関係
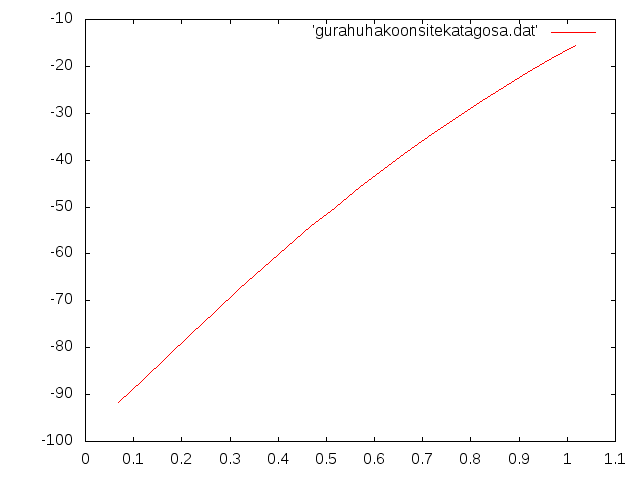
鋼材と木材で箱型断面h2†
- b1=0.84m,b2=0.009m
- h1=0.009m,h2=0.18mから0.05m刻みで1.018mまで増加させた
- オンサイトのh2初期値=0.5m
- 厚さは全て同じ
| h2(m) | 相対誤差(%) |
| 6.80000E-02 | -9.16908E+01 |
| 1.18000E-01 | -8.69721E+01 |
| 1.68000E-01 | -8.20985E+01 |
| 2.18000E-01 | -7.72230E+01 |
| 2.68000E-01 | -7.24022E+01 |
| 3.18000E-01 | -6.76740E+01 |
| 3.68000E-01 | -6.30595E+01 |
| 4.18000E-01 | -5.85704E+01 |
| 4.68000E-01 | -5.42178E+01 |
| 5.18000E-01 | -5.00031E+01 |
| 5.68000E-01 | -4.59331E+01 |
| 6.18000E-01 | -4.20035E+01 |
| 6.68000E-01 | -3.82223E+01 |
| 7.18000E-01 | -3.45813E+01 |
| 7.68000E-01 | -3.10793E+01 |
| 8.18000E-01 | -2.77155E+01 |
| 8.68000E-01 | -2.44874E+01 |
| 9.18000E-01 | -2.13888E+01 |
| 9.68000E-01 | -1.84182E+01 |
| 1.01800E+00 | -1.55690E+01 |
- 相対誤差と高さh2の関係
鋼材箱型断面h2†
- b1=0.84m,b2=0.009m
- h1=0.009m,h2=0.18mから0.05m刻みで増加させた
- オンサイトのh2初期値=0.5m
| h2(m) | 相対誤差(%) |
| 6.80000E-02 | -5.45343E+00 |
| 1.18000E-01 | -3.88840E+00 |
| 1.68000E-01 | -3.48379E+00 |
| 2.18000E-01 | -3.25848E+00 |
| 2.68000E-01 | -3.06076E+00 |
| 3.18000E-01 | -2.86775E+00 |
| 3.68000E-01 | -2.66288E+00 |
| 4.18000E-01 | -2.44449E+00 |
| 4.68000E-01 | -2.20650E+00 |
| 5.18000E-01 | -1.95315E+00 |
| 5.68000E-01 | -1.67852E+00 |
| 6.18000E-01 | -1.38560E+00 |
| 6.68000E-01 | -1.06950E+00 |
| 7.18000E-01 | -7.40961E-01 |
| 7.68000E-01 | -3.85094E-01 |
| 8.18000E-01 | -1.02293E-02 |
| 8.68000E-01 | 3.84346E-01 |
| 9.18000E-01 | 7.99488E-01 |
- 相対誤差と高さh2の関係
ccx†
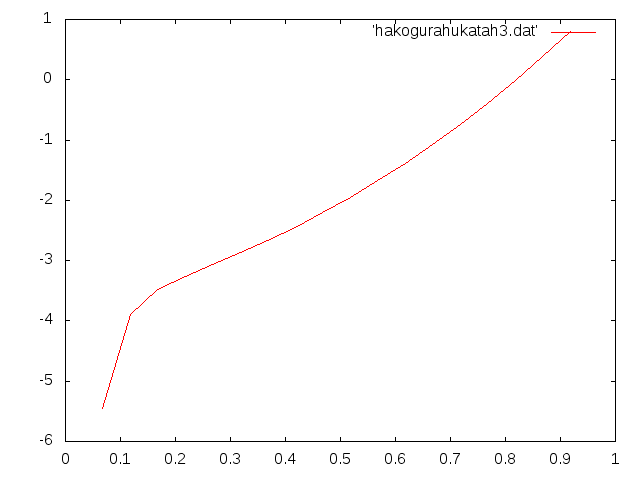
鋼材箱型断面h2†
- cowperb=0.849(m)
- 厚さ=9.0E-03(m)
- ティモシェンコ理論値とfortran calculixの比較
- 赤線:ティモシェンコ,緑線:fortran calculix
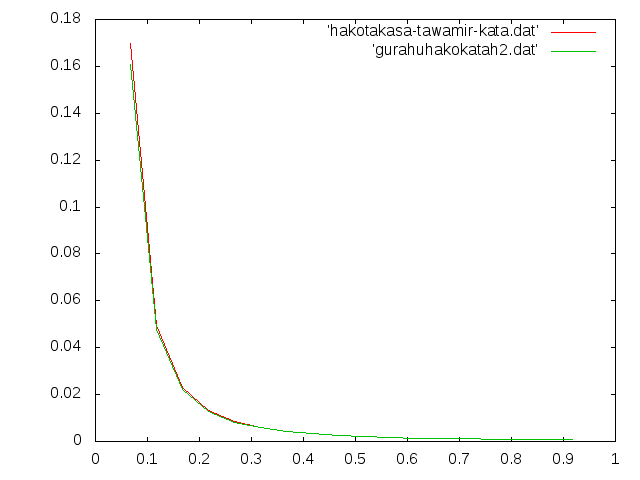
- 縦軸:たわみ(m),横軸:h2(m)
- 相対誤差とたわみ

| h2(m) | 相対誤差(%) |
| 6.80000E-02 | -5.45343E+00 |
| 1.18000E-01 | -3.88840E+00 |
| 1.68000E-01 | -3.48379E+00 |
| 2.18000E-01 | -3.25848E+00 |
| 2.68000E-01 | -3.06076E+00 |
| 3.18000E-01 | -2.86775E+00 |
| 3.68000E-01 | -2.66288E+00 |
| 4.18000E-01 | -2.44449E+00 |
| 4.68000E-01 | -2.20650E+00 |
| 5.18000E-01 | -1.95315E+00 |
| 5.68000E-01 | -1.67852E+00 |
| 6.18000E-01 | -1.38560E+00 |
| 6.68000E-01 | -1.06950E+00 |
| 7.18000E-01 | -7.40961E-01 |
| 7.68000E-01 | -3.85094E-01 |
| 8.18000E-01 | -1.02293E-02 |
| 8.68000E-01 | 3.84346E-01 |
| 9.18000E-01 | 7.99488E-01 |
応急橋の片持ちモデルh2†
- nz=512で固定、桁高=0.3~0.9mmまで
| h2(m) | たわみ(m) |
| 0.3 | 1.2162E-02 |
| 0.4 | 6.7682E-03 |
| 0.5 | 4.5888E-03 |
| 0.6 | 3.4692E-03 |
| 0.7 | 2.8055E-03 |
| 0.8 | 2.3735E-03 |
| 0.9 | 2.0733E-03 |
オンサイトの片持ちモデルh2†
- nz=512で固定、桁高=0.3~0.9mまで
| h2(m) | たわみ(m) |
| 0.3 | 2.4269E-02 |
| 0.4 | 1.0855E-02 |
| 0.5 | 5.9180E-03 |
| 0.6 | 3.6444E-03 |
| 0.7 | 2.4355E-03 |
| 0.8 | 1.7259E-03 |
| 0.9 | 1.2785E-03 |
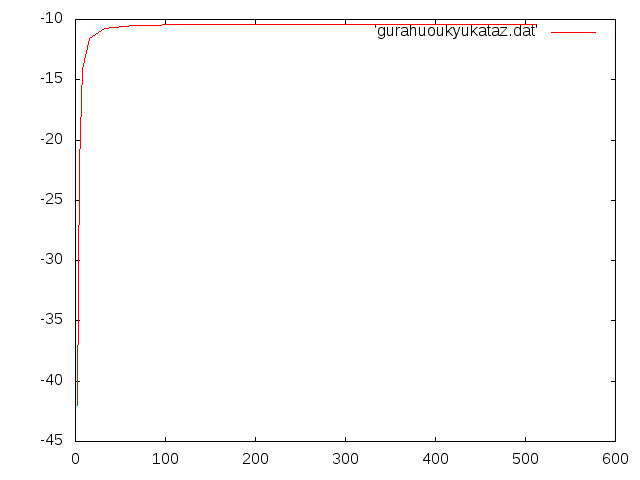
応急橋片持ちモデルnz†
| nz | たわみ(m) | 相対誤差(%) |
| 2 | 3.5446E-03 | -41.992 |
| 4 | 4.7644E-03 | -22.029 |
| 8 | 5.2480E-03 | -14.115 |
| 16 | 5.4036E-03 | -11.569 |
| 32 | 5.4524E-03 | -10.770 |
| 64 | 5.4686E-03 | -10.505 |
| 128 | 5.4742E-03 | -10.413 |
| 256 | 5.4758E-03 | -10.387 |
| 512 | 5.4736E-03 | -10.379 |
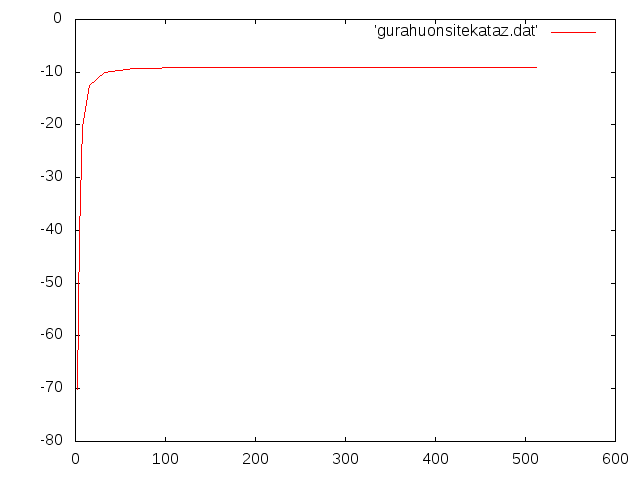
オンサイト片持ちモデルnz†
| nz | たわみ(m) | 相対誤差(%) |
| 2 | 1.9384E-03 | -70.196 |
| 4 | 3.8697E-03 | -40.502 |
| 8 | 5.1826E-03 | -20.316 |
| 16 | 5.6916E-03 | -12.489 |
| 32 | 5.8493E-03 | -10.065 |
| 64 | 5.8966E-03 | -9.3375 |
| 128 | 5.9114E-03 | -9.1099 |
| 256 | 5.9163E-03 | -9.0346 |
| 512 | 5.9180E-03 | -9.0084 |
salome練習†
- 梁断面は横長,正方形,縦長
- スパンell=200×1000
- 荷重P=10N
- ヤング率E=3GPa,ポアソン比ν=0.3
①b=30×1000,h=5×1000(横長)†
- 理論値=2.8458E-02m
| length | 要素数 | たわみ(m) | 相対誤差(%) |
| 20000 | 398 | 1.5654E-03 | -96.488 |
| 15000 | 514 | 3.5413E-03 | -87.531 |
| 10000 | 1256 | 6.5277E-03 | -77.015 |
| 5000 | 5304 | 1.0370E-02 | -63.486 |
| 2500 | 21767 | 1.7528E-02 | -38.282 |
| 1200 | 173811 | 2.5647E-02 | -9.6937 |
| 1000 | 176011 | 2.5657E-02 | -9.6585 |
| 800 | 184862 | 2.5674E-02 | -9.5986 |
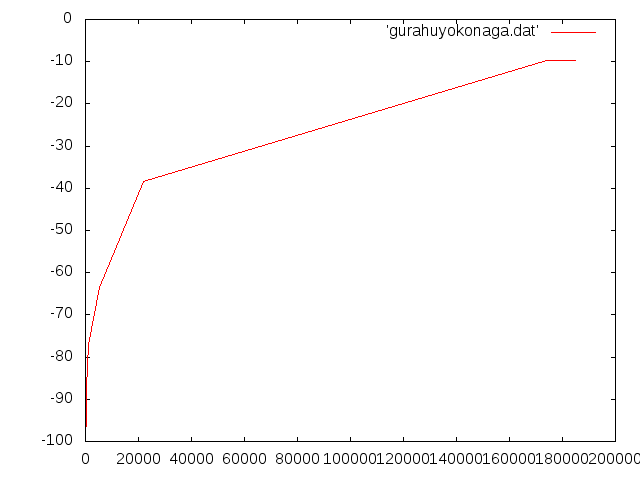
②b=20×1000,h=20×1000(正方形)†
- 理論値=6.7187E-04m
| length | 要素数 | たわみ(m) | 相対誤差(%) |
| 20000 | 373 | 3.5819E-04 | -46.688 |
| 15000 | 584 | 4.0795E-04 | -39.281 |
| 10000 | 1761 | 5.1320E-04 | -23.616 |
| 5000 | 8128 | 5.9328E-04 | -11.697 |
| 2500 | 41234 | 6.2908E-04 | -6.3688 |
| 1200 | 190758 | 6.5535E-04 | -2.4588 |
| 1000 | 343661 | 6.6252E-04 | -1.3916 |
| 800 | 389934 | 6.6245E-04 | -1.4021 |
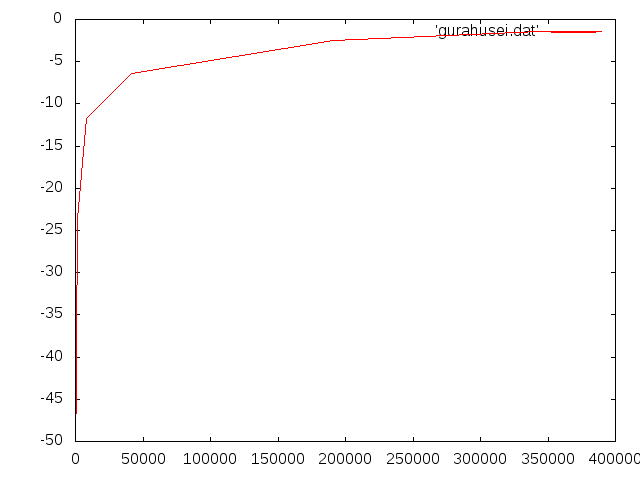
③b=5×1000,h=30×1000(縦長)†
- 理論値=8.0487E-04m
| length | 要素数 | たわみ(m) | 相対誤差(%) |
| 20000 | 380 | 5.1029E-04 | -36.600 |
| 15000 | 482 | 5.8365E-04 | -27.485 |
| 10000 | 1226 | 7.2589E-04 | -9.8128 |
| 5000 | 5229 | 7.7913E-04 | -3.1980 |
| 2500 | 21510 | 7.9245E-04 | -1.5431 |
| 1200 | 149064 | 7.9837E-04 | -0.8758 |
| 1000 | 150875 | 7.9834E-04 | -0.81131 |
| 800 | 157030 | 7.9845E-04 | 0.79764 |
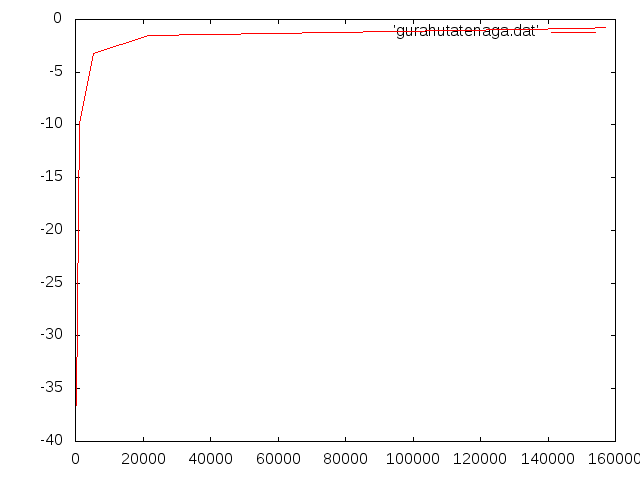
- モデルにかかわらずlenghを小さくしていくたびに理論値に近づいていく傾向があるが、断面が正方形と縦長の場合、lengthとたわみの関係のみに着目するとlengh1000のとき前後とのたわみの大小関係?がおかしくなっている。もしかしたらモデルの形、節点数や要素数と関係があるのかも(13/6/15)
- グラフにしてみるとあまり気にならない?(13/6/17)
ccx練習(アクリル板による片持ち梁のたわみと分割数の関係)†
- 梁断面は横長,正方形,縦長の3種
- スパンell=200mm
- 荷重P=10N
- ヤング率E=3GPa,ポアソン比ν=0.3
- nx=10,ny=20で固定,nzを10~500まで
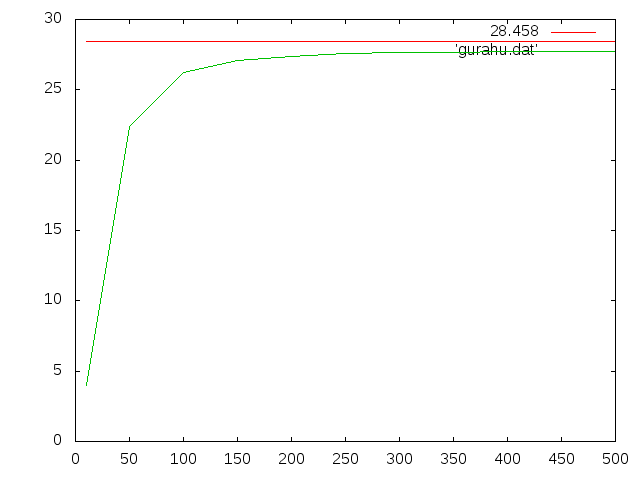
①b=30mm,h=5mm(横長)†
- 理論値=28.458mm(せん断たわみも考慮)
②b=20mm,h=20mm(正方形)†
- 理論値=0.67187mm(せん断たわみも考慮)
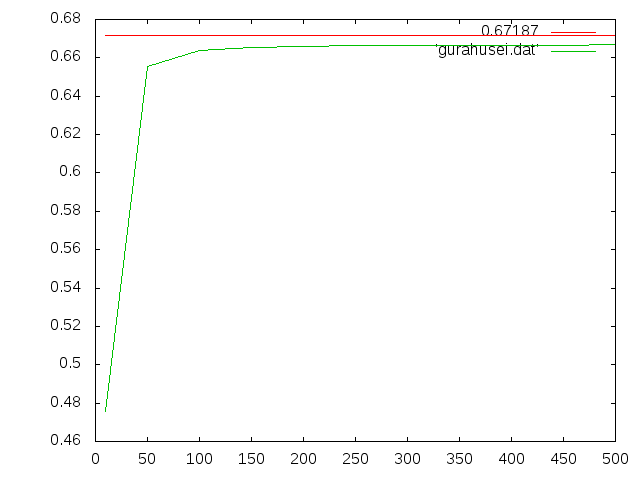
- 縦軸:たわみ(mm),横軸:nz
③b=5mm,h=30mm(縦長)†
- 理論値=0.80487mm(せん断たわみも考慮)
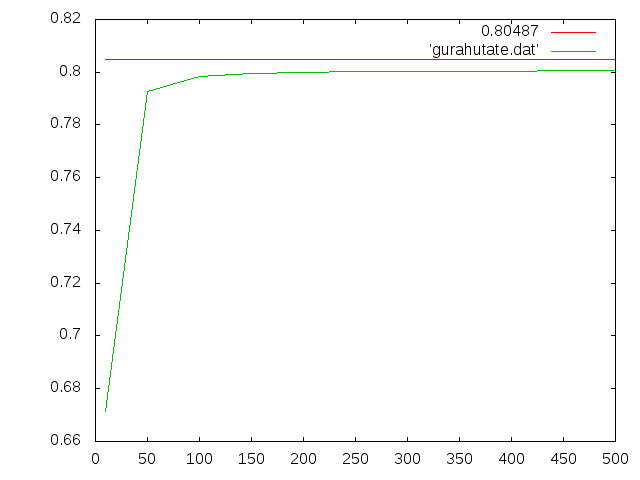
- 縦軸:たわみ(mm),横軸:nz
ccx練習†
- 梁断面は横長,正方形,縦長の3種
- スパンell=150mm
- 荷重P=20N
- ヤング率E=200GPa,ポアソン比ν=0.3
b=50mm,h=5mm片持ち梁グラフ†
- 理論値=0.21600624mm
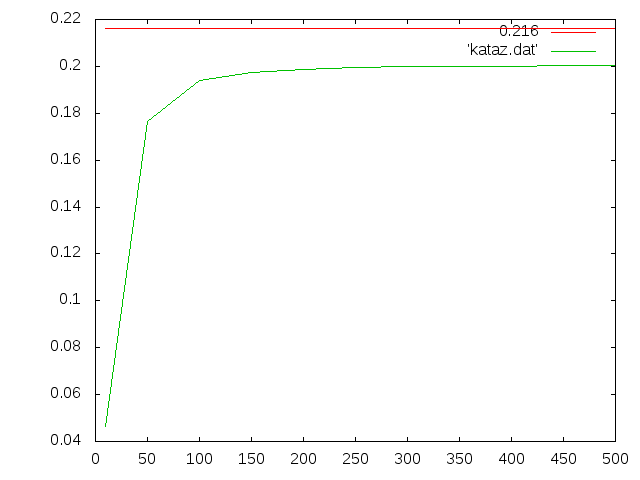
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)

