当面の課題†
20/5/11(後藤)†
- 弾塑性解析ができるか確認(小川さん、佐藤さん、吉田さんで情報共有)
- SALOME-Mecaの使用法解説の塑性変形の基本(1)の片持ち梁の例題が解けるかどうかやってみる。軸方向\( z \), たわみ方向\( y \)としてほしい。
- 固定端の引っ張り側の縁部の応力が、降伏点(105MPa)に達するまでは、\( \sigma=\frac{M}{I}y \)で求まる理論値と合うか確認
- 荷重(縦軸)、先端のたわみ(横軸)でグラフを描き、固定端が降伏点に達する荷重までは線形、その後は、傾きが寝てくるか確認
- 以上が確認できたら、片持ち梁の弾塑性解析のhdfファイル(計算前のもの)をSalome-Meca例題ファイルの弾塑性解析のところにアップ。
20/5/18†
- (x,y,z)=(10,20,100)のboxを作成し、メッシュサイズは1にした。
- メッシュを作成して保存し、サーバーを閉じようとしたら、固まってしまった。
- 強制終了して/home/salome_meca/appli_V2017/salomeで起動しメッシュの作成まで行ったが、固まらなかった。
- 起動した時に端末にメッセージが表示された。
Warning: this type (Study,objref) already exists, it will be ignored.
found in 20.5 seconds
Start SALOME, elapsed time : 21.8 seconds
[#p5f7e7ba]
Warning: HYBRIDPLUGIN GUI resources are not found. [#va5afeb0]
HYBRIDPLUGIN GUI will not be available. [#n38190e5]
[#jf596eb1]
[#z664fb54]
Warning: BLSURFPLUGIN GUI resources are not found. [#r598ea36]
BLSURFPLUGIN GUI will not be available. [#h0f5c81d]
[#x05d1df1]
[#q3e1609c]
Warning: HexoticPLUGIN GUI resources are not found. [#m9b53a40]
HexoticPLUGIN GUI will not be available. [#m001e348]
[#e1fbd5a5]
[#r94e0fd1]
Warning: NETGENPLUGIN GUI resources are not found. [#nfd376be]
NETGENPLUGIN GUI will not be available. [#ac3e85e8]
[#tfc991fb]
[#i0dc08d4]
Warning: GHS3DPLUGIN GUI resources are not found. [#xe2ff960]
GHS3DPLUGIN GUI will not be available. [#q2a11c06]
[#yba6c902]
20/5/21†
- AsterSutudyのDEFI_FONCTIONが見つからない
20/5/28†
- 6-5のCALC_ELEM、CALC_NOが見つからず、調べたところ、「バージョン10まではポスト処理コマンドは、CALC_ELEM、CALC_NOの2つに分かれていたが、バージョン11以降では、CALC_CHAMPに統合された。」とあったので、CALC_CHAMPを選択して進めていった。
- 解析を実行したが、Outputのところに不備があり、赤色になった。
- b_not_resueやb_noilなど、b_で始まるコマンドがほとんど見つからなかった。これもバージョンによる違いなのかもしれない。来週までに調べておく。
20/6/5†
20/6/12†
- BC and Loadのところに不備があり、直したら青色になった。来週はParavisで変位を確認する。
20/6/19†
- ParaVisでTimeを動かし、変位を確認することができた。来週はその変位を表とグラフでまとめる。
20/6/26†
20/6/30†
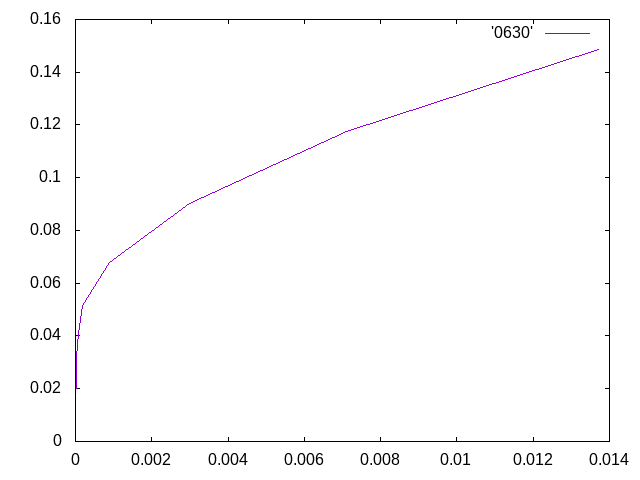
- 縦軸が応力、横軸がひずみのグラフを作成した。グラフの傾きはだんだんと寝てきたが、明確な降伏点はわからなかった。
20/7/10†
- functions and listsのlistrのDEFI_LIST_REELのPASを0.1から0.01に直して計算してみたが、黄色のマークになった。
- Timeの10分割を変える方法が分からなかったので、PASを0.01、JUSQU_Aを0.1に変えてみたら青色になった。これで1の10分割から0.1の10分割になったはずなので、この値を使ってグラフを作成する。
20/7/15†
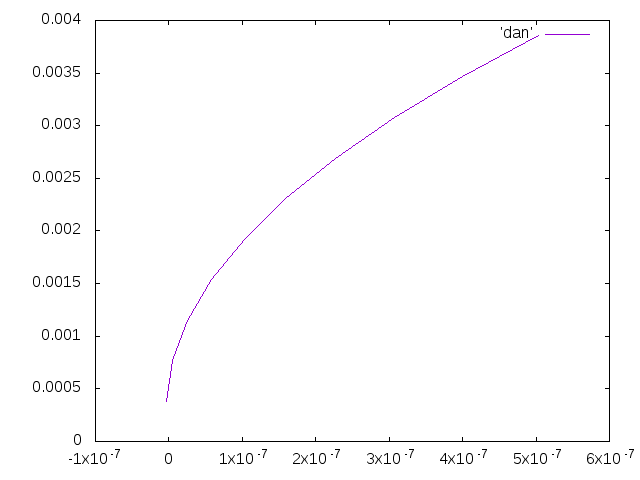
- 根元の応力が105MPaになるときの荷重を計算したところ、荷重は700Nになったので、その1割増しの770Nの荷重をかけて計算した。そして、その計算結果をグラフで表した。縦軸は根元の応力、横軸は先端のひずみである。
20/7/21†
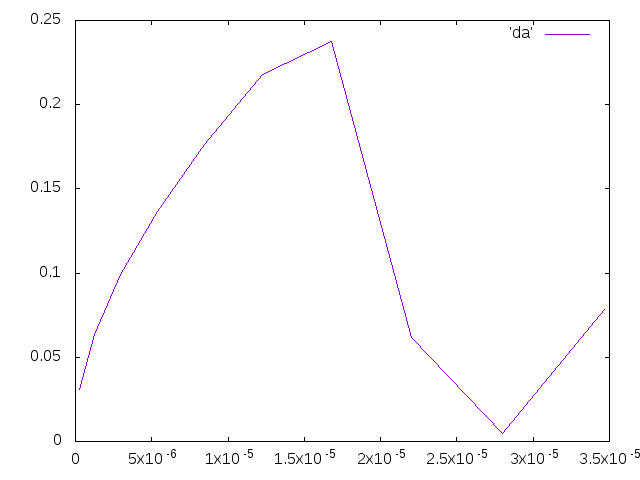
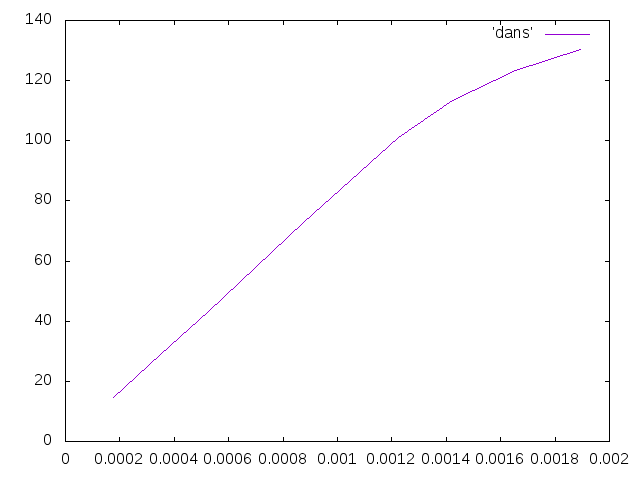
- 前回は応力とひずみの向きを考慮していなかったので、それを踏まえてもう一回計算し直したところ、下のグラフのようになった。
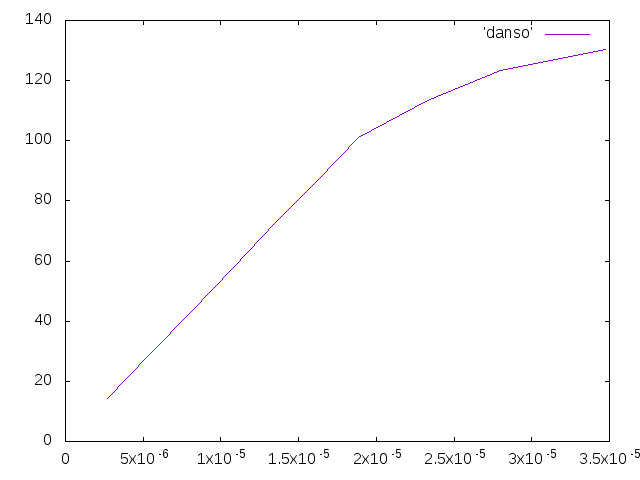
- 上のグラフは先端のひずみで計算していたので、根元のひずみで計算しなおした。応力が101MPa、ひずみが0.0012あたりからグラフは線形ではなくなった。
20/7/24†
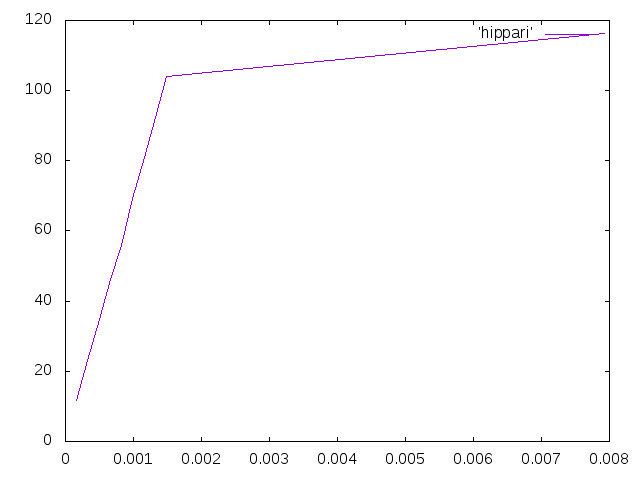
- 梁を軸方向に引っ張ったときの解析を行った。引張応力が105MPaになる時の荷重は21000Nで、その1割増しの23200Nの荷重をかけて計算した。計算結果のグラフは以下のとおりである。縦軸は先端の応力、横軸は先端のひずみである応力が104MPa、ひずみが0.0015あたりまではグラフは線形になっていた。そこからグラフの線はほぼ横ばいになっている。
20/8/7†
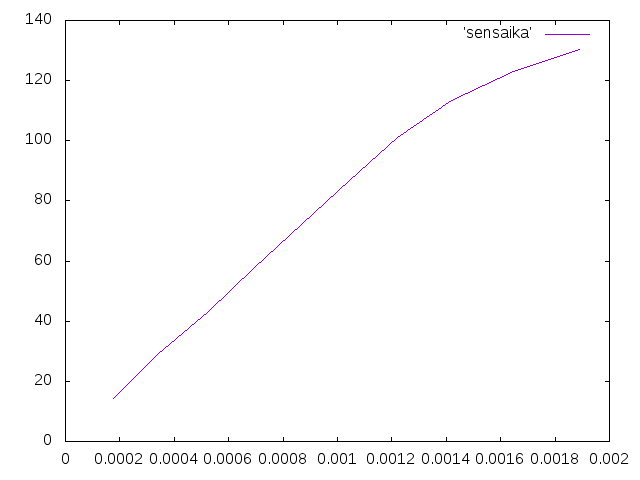
- 今までは面に載荷していたが,集中荷重なので線載荷にしてみた.計算結果をグラフに表したが,面載荷とほとんど変わらなかった.
20/10/4†
- Geometryで床版、主プレート、補助プレート、補助金具、支柱まで作成したが、どこの接合部がくっついていてよいのか分からない。(床版とプレートは離れていなければならないが、プレートと支柱はくっついていてよいのかなど)
20/10/7†
- 鋼材のメッシュサイズを決めるために支柱のみの解析をした.
- 支柱を長さ600mmの円筒型の片持ち梁と仮定して理論値を計算した.荷重は1N,sm400のヤング率の210000MPaを代入して計算したところ,変位は0.000146mmとなった.
- 理論値計算と同じ条件で解析した.ポアソン比は0.3とした.結果は図のようになった.
| メッシュサイズ | 変位 |
| 6 | 0.000154 |
| 7 | 0.00015381 |
| 8 | 0.00015373 |
| 9 | 0.00015379 |
| 10 | 0.00015365 |
| 11 | 0.00015372 |
| 12 | 0.0001538 |
- メッシュサイズが1の時は他のサイズと同じ条件でも計算できなかった.
- この結果から,メッシュサイズが10の時に理論値に一番近くなることが分かった.その時の相対誤差は5.2%だった.
20/10/8†
- CLTを長さ2000mmの単純梁として手計算をした.
- 荷重は1N,断面二次モーメントは281250000mm4とした.
- CLTの等級は異等級構成Mx60A(中村先生)
- CLTメモの等級ごとのヤング率の求め方の表3より,Mx60の5層5プライの曲げヤング係数の平均値が4.2GPaだったため,その数値を今回のヤング率とした.
- 計算したところ,変位は0.000423mmとなった.
20/10/9†
- 鋼材のヤング率は正しくは206GPaだったので,その数値で理論値の計算をしたら,変位は0.000149mmとなった.
20/10/12†
- 鋼材の正しいヤング率で解析した.結果は図のようになった.
| メッシュサイズ | 変位 |
| 6 | 0.000157 |
| 7 | 0.0001568 |
| 8 | 0.0001567 |
| 9 | 0.0001568 |
| 10 | 0.0001566 |
| 11 | 0.0001567 |
| 12 | 0.0001568 |
- メッシュサイズが10の時に理論値に一番近くなった.相対誤差は5.1%になった.
- 直交集成板の日本農林規格によると,「直交集成板を構成する各ラミナの厚さは原則として等厚であること」と書いてあった.URLはCLTメモに貼り付けた.
- Mx 60は外層ラミナの強度等級がM60A、内層ラミナの強度等級がM30A(CLTメモの等級ごとのヤング率の求め方など)
- M60A,M30Aのヤング率の基準値は直交集成板の日本農林規格に書いてある.
20/10/14†
- M60A,M30Aのヤング率をそれぞれ6.0GPa,3.0GPaとしてMx60のヤング率を計算した.
- Shear Analogy Methodという方法で計算した.有効曲げ剛性(EI)effは,1335600000GPa*mm4となった.
- この有効曲げ剛性をCLT全体の断面二次モーメントで割ったところ,ヤング率Eeffは4.8704GPaとなった.
- 有効せん断剛性も求めた.
- 繊維方向のヤング率と各方向のせん断弾性係数の関係式を用いて各ラミナのせん断弾性係数を求めた.それを使って有効せん断剛性(GA)effを求めたところ,4186047MPa*mm4となった.
- 求めた剛性を使ってCLTの変位を求めた.荷重は梁の中心に1N,梁の長さは桁の中心間の2000mm,せん断補正係数は5/6として,単純梁として求めた.変位は0.00026812mmとなった.
20/10/16†
- メッシュサイズを更に増やして支柱の解析をした.結果は図とグラフの様になった.
| メッシュサイズ | 要素数 | 変位 |
| 5 | 145813 | 0.000157025 |
| 6 | 144052 | 0.0001569962 |
| 7 | 38244 | 0.0001567935 |
| 8 | 37009 | 0.0001567133 |
| 9 | 36804 | 0.0001567753 |
| 10 | 36116 | 0.000156634 |
| 11 | 36035 | 0.0001567057 |
| 12 | 35293 | 0.0001567914 |
| 15 | 9570 | 0.0001533965 |
| 20 | 9148 | 0.0001537212 |
| 25 | 8747 | 0.0001540633 |
| 30 | 2972 | 0.0001336225 |
| 35 | 2364 | 0.0001379303 |
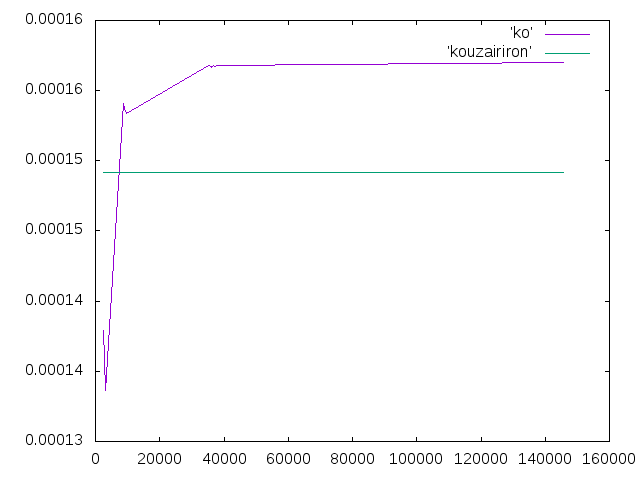
- このグラフから,要素数を増やすと0.000157当たりに収束していることが分かる.
20/10/19†
- CLTの方の解析をした.メッシュサイズを20にしたところ,要素数が300万を超え,計算に時間がかかった.次回は要素数をもっと少なくして計算する.
- メモリの上限を超えているというメッセージが出た.
Error during the dynamic allocation. It was not possible to allocate !
! a memory zone length 1169 Mo, one exceeds the maximum limit !
! built-in with 1493 Mo and one occupies already 580 Mo. !
! The last operation of memory deallocation made it possible to recover 562 Mo. !
!--------------------------------------------------------------------------------!
20/10/20†
20/10/21†
- 横2ミリ,縦1ミリの穴を横20ミリ,縦10ミリの大きさにしてみたら昨日よりも時間がかからずにメッシュを作成することができた.実際の床版のモデルにもボルトを通すために直径26ミリの穴が開いているので,影響は無いと考えた.
- 解析結果は図とグラフのようになった.
| メッシュサイズ | 要素数 | 変位 |
| 14 | 581948 | 0.0001126382 |
| 15 | 443110 | 0.0001150793 |
| 20 | 335445 | 0.0001133839 |
| 25 | 255690 | 0.0001076753 |
| 27 | 131296 | 0.0001036925 |
| 30 | 83221 | 0.000097703671 |
| 40 | 63683 | 0.000095167519 |
| 50 | 54909 | 0.000093780481 |
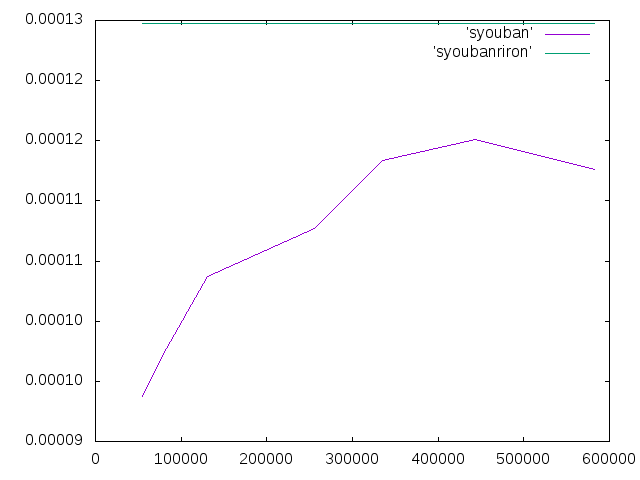
- CLTを等方性としてたわみを計算しなおしたら,0.0001247878となったので理論値はその値にした.
20/10/28†
- 支柱にブラケットをつけて計算し直した.
- ブラケットは一辺90ミリの立方体とした.等方性としたのでヤング率は4870MPa,ポアソン比は0.4とした.
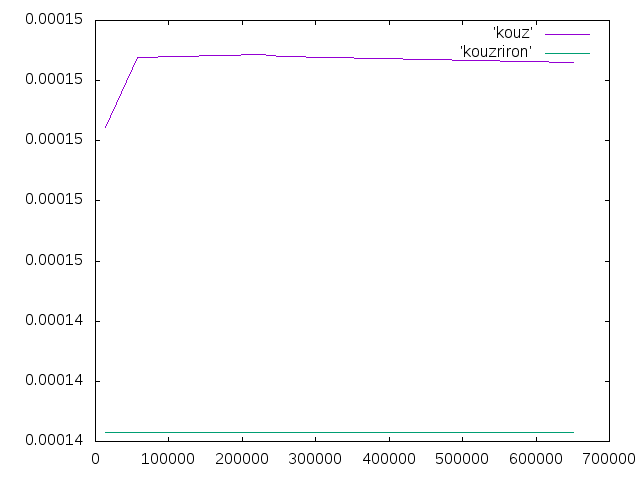
- 支柱の高さ588ミリの部分にグループを作成し,そこの変位を平均した.結果はグラフと表のようになった.
| メッシュサイズ | 要素数 | 変位 |
| 3 | 650732 | 0.0001525962 |
| 4 | 253843 | 0.0001528185 |
| 5 | 226615 | 0.000152853 |
| 10 | 57390 | 0.0001527818 |
| 20 | 13573 | 0.0001504562 |
20/10/29†
- プレートと床版が一体化していない状態で解析する必要があるため,SalomeMecaの使用法解説の接触解析の基本(1)をした.例題データを読み込み,メッシュを切り,ジオメトリのグループを作成した.
- AsterStudyはMATE=AFFE_MATERIAUまでやった.
20/10/30†
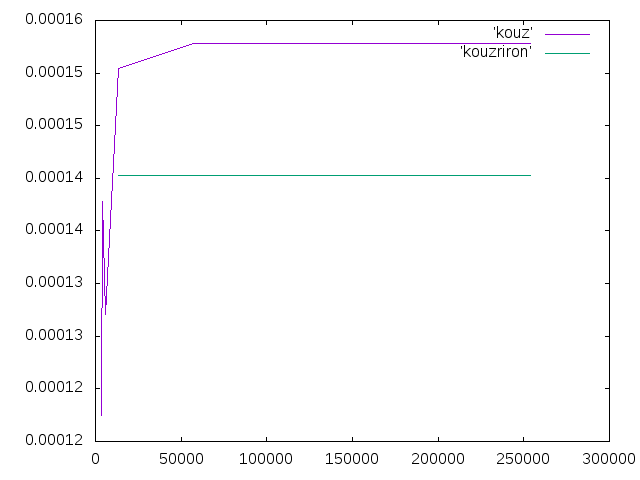
- 支柱のメッシュをもっと粗くして計算しなおした.結果は表とグラフのようになった.
- グラフを見やすくするためにメッシュサイズ3のときの変位は消してある.
| メッシュサイズ | 要素数 | 変位 |
| 3 | 650732 | 0.0001525962 |
| 4 | 253843 | 0.0001528185 |
| 5 | 226615 | 0.000152853 |
| 10 | 57390 | 0.0001527818 |
| 20 | 13573 | 0.0001504562 |
| 30 | 5931 | 0.0001270705 |
| 40 | 3982 | 0.0001377993 |
| 50 | 3411 | 0.0001174439 |
20/11/2†
- 接触解析の基本(2)の荷重拘束
- CONTACTの代わりにDEFI-CONTACTを接触の設定として用いた.
- 接触の部分はSalomeMecaの使用法解説の接触解析の基本(2)を,非線形の部分は弾塑性解析の練習で使ったhdfファイルを参考にした.
- 黄色マークで下のようなメッセージが出た.
S> Exception user raised but not interceptee. !
! The bases are fermees. !
! Type of the exception: ArretCPUError !
! [('?', (), (), ())]
- このメッセージの意味はよく分からなかった.
- Salome接触解析メモを見たところ,部材ごとでメッシュを切らないといけないことがわかった.
20/11/3†
- 床版のメッシュを粗くして計算しなおした.結果は表とグラフのようになった.
| メッシュサイズ | 要素数 | 変位 |
| 14 | 581948 | 0.0001126382 |
| 15 | 443110 | 0.0001150793 |
| 20 | 335445 | 0.0001133839 |
| 25 | 255690 | 0.0001076753 |
| 27 | 131296 | 0.0001036925 |
| 30 | 83221 | 0.000097703671 |
| 40 | 63683 | 0.000095167519 |
| 50 | 54909 | 0.000093780481 |
| 60 | 21413 | 0.000076680678 |
| 70 | 18683 | 0.000073994244 |
| 80 | 16084 | 0.000072255257 |
| 100 | 14087 | 0.000070051691 |
| 150 | 5070 | 0.000042707938 |
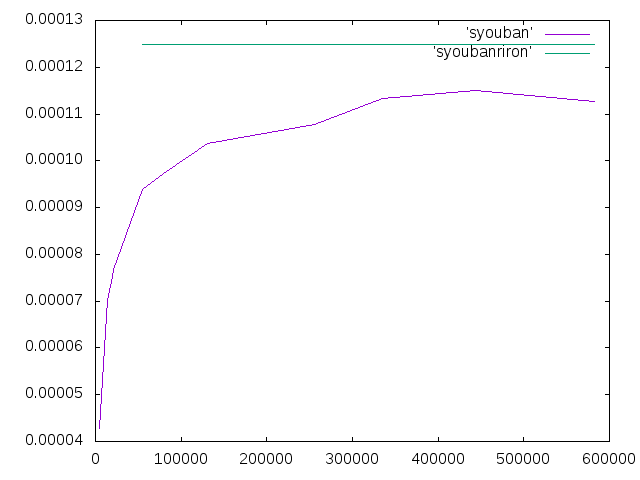
- 計算し直す前よりは収束している様子を再現することが出来た.
- 一応半解析の方もやってみた.床版を半分に切断し,切断面を載荷面とした.載荷面はxy方向を固定してz方向だけ動けるようにした.計算は出来たが,要素数が60万くらいのときに変位が0.0002くらいになった.切断する前の床版よりも誤差が大きくなってしまった.
- 切断面にも穴を開けて載荷線を作るという方法でやってみた.計算できず,下のようなエラーメッセージが出た.
S> Exception user raised but not interceptee. !
! The bases are fermees. !
! Type of the exception: error !
! !
! Problème : la matrice est singulière ou presque singulière : !
! Lors de la factorisation de la matrice, on a rencontré un problème !
! (pivot nul ou presque nul) à la ligne 37413 qui correspond au degré de liberté !
! donné ci-dessus. !
! Le nombre de décimales "perdues" pour cette ligne est : 13. !
! Ce nombre de décimales perdues est lié au degré de singularité de la matrice. !
! Plus il est grand, plus le système est singulier. !
! Quand on a perdu plus de 8 décimales, on estime que l'on a perdu 50% de la !
! précision !
! des nombres réels (qui ont 15 décimales environ). !
! !
! Risques et conseils : !
! * Si la ligne correspond a un degré de liberté physique, il s'agit !
! probablement d'un mouvement !
! de corps rigide mal bloqué. !
! Vérifiez les conditions aux limites. !
! Si vous faites du contact, il ne faut pas que la structure ne "tienne" que !
! par le contact. !
! Vérifiez également les caractéristiques matériaux (module d'Young, ...). !
! !
! * Si la ligne correspond a un degré de liberté de Lagrange, il s'agit sans !
! doute d'une condition !
! limite redondante. !
! En particulier, il se peut que la relation linéaire surabondante provienne !
! des conditions de contact. !
! Peut-être devriez vous exclure certains noeuds des conditions de contact !
! (mots clés SANS_NOEUD et SANS_GROUP_NO). !
! !
! * Si le solveur utilisé est LDLT ou MULT_FRONT, vous pouvez utiliser le !
! solveur MUMPS !
! car celui-ci est le seul à pouvoir factoriser les matrices qui ne sont pas !
! définies positives. !
! !
! * Parfois, en parallèle, le critère de détection de singularité de MUMPS est !
! trop pessimiste ! Il reste néanmoins souvent !
! possible de faire passer le calcul complet en relaxant ce critère !
! (augmenter de 1 ou 2 la valeur du mot-clé NPREC) ou !
! en le débranchant (valeur du mot-clé NPREC=-1) ou en relançant le calcul !
! sur moins de processeurs. !
! !
! * Il se peut aussi que ce phénomène soit tout à fait normal avec X-FEM si la !
! fissure passe !
! très près d'un noeud. !
! Si le nombre de décimales perdues n'est pas trop grand (max 10 décimales), !
! vous pouvez relancer le calcul en augmentant le nombre de décimales perdues !
! autorisé : !
! mot-clé NPREC du mot clé facteur SOLVEUR. !
! Sinon, contactez l'équipe de développement.
- 載荷線のxy方向の固定を解除してみたが,同じメッセージが出た.
20/11/6†
- ティモシェンコ梁で理論値の計算をした.
- せん断補正係数は,ポアソン比の0.3を代入して0.5306122449になった.
- せん断補正係数とせん断弾性係数(79GPa)を代入して計算したところ,変位は0.0001426492498となった.2✕10-6ほどしか変わらなかった.
- 支柱の長さを10倍ほどにして解析した.メッシュサイズを10,40,50で作成してみたが,10の時は作成が終わらず,40と50の時はエラーが出た.
- 10のときに保存しないまま強制終了したのでそのときのhdfファイルなどはない.
20/11/8†
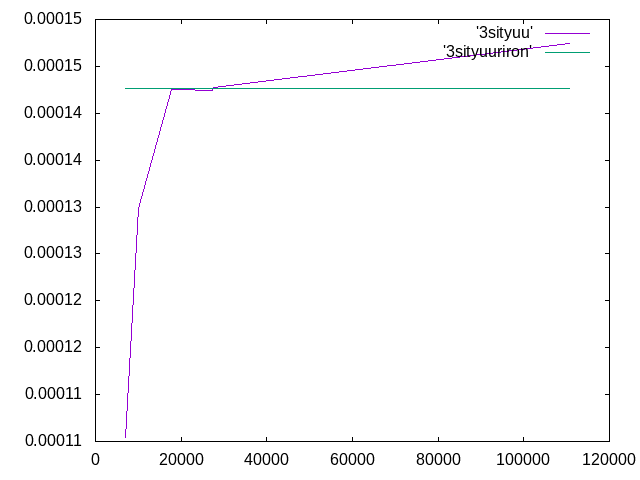
- 10倍だとできなかったので、とりあえず3倍でやってみることにした。ブラケットなしのほうが理論値に近くなると思い、ブラケットとふたを外して解析した。結果は表とグラフのようになった。
| メッシュサイズ | 要素数 | 変位 |
| 10 | 110765 | 0.00014746275 |
| 20 | 27475 | 0.00014276444 |
| 21 | 27419 | 0.000142449056 |
| 23 | 19402 | 0.000142579938 |
| 25 | 17792 | 0.0001425346 |
| 30 | 10050 | 0.00012982425 |
| 40 | 6912 | 0.000105412889 |
20/11/11†
- 接触解析の基本(1)(摩擦なし)の続き
- MODI_MAILLAGE: メッシュの操作
- 接触解析メモにMODI_MAILLAGEがなかったのでその項目を消して解析してみた.ほかは接触解析の基本(1)の通り.しかし結果は黄色だった.
<ArretCPUError> <MECANONLINE9_1> !
! !
! Arrêt par manque de temps CPU pendant les itérations de Newton, au numéro d'instant < 1 > !
! - Temps moyen par itération de Newton : 81.619164 !
! - Temps restant : 130.515530 !
! La base globale est sauvegardée. Elle contient les pas archivés avant l'arrêt. !
! !
! Conseil : !
! - Augmentez le temps CPU. !
!-------------------------------------
- このようなエラーメッセージが出た.CPU時間を増やすということが書いてあったので,HistoryViewのtimeを15から30に増やして解析した.赤色になった.
- timeを15に戻し,STAT_NON_LINE(非線形解析の設定)を弾塑性解析の設定でやってみたり解説に書いてあるとおりにやってみたりしているが,何度やっても黄色マークのまま.
20/11/12†
- 今までやっていた接触解析のモデルはSTEPファイルを読みこんだものなので一つずつメッシュを切ることが出来なかった.寸法が書いてなかったのでGeometryで一から作ることもできなかった.そこで,荷重拘束の接触解析(摩擦あり)のペナルティ法のモデルは寸法が書いてあったのでそれを一から作り,摩擦ありの接触解析を行うことにした.
- 荷重拘束の接触解析(摩擦あり)のペナルティ法
- Geometry:baceとtopの対称面はそれぞれでグループ化した.
- Mesh:メッシュ→アセンブリをビルドでコンパウンドを作成.Geometryでそれぞれグループ化した対称面はコンパウンドを作ったらひとつになった.
- AsterStudy:2.5次要素への変換は、CREA_MAILLAGEコマンドを用いる
20/11/13†
- 床版(単純梁)の解析
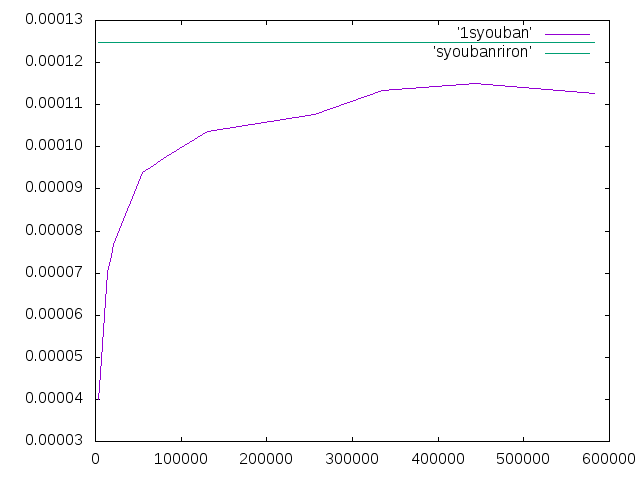
- ふたつ目の固定線が全方向拘束されていたので,kotei2のy方向の拘束を外した.結果は表とグラフのようになった.
- 外す前とほとんど変化はなかった.
- 理論値に一番近い値のときの相対誤差は-7.78%だった.
| メッシュサイズ | 要素数 | 変位 |
| 14 | 581948 | 0.0001126387 |
| 15 | 443110 | 0.0001150798 |
| 20 | 335445 | 0.000113384 |
| 25 | 255690 | 0.000107676 |
| 27 | 131296 | 0.0001036928 |
| 30 | 83221 | 0.000097704057 |
| 40 | 63683 | 0.000095167927 |
| 50 | 54909 | 0.000093780519 |
| 60 | 21413 | 0.000076680739 |
| 70 | 18683 | 0.000073994344 |
| 80 | 16084 | 0.000072255329 |
| 100 | 14087 | 0.0000700518 |
| 150 | 5070 | 0.000042708863 |
| 200 | 3587 | 0.00003988833 |
- 二次要素への変換方法
- 作成された二次要素を右クリック→二次/一次要素への変換→二次要素へ変換します→適用して閉じる
20/11/16†
- 二次要素への変換
- メッシュサイズ40の支柱モデルを二次要素に変換したら警告メッセージが出た.
「ノードが (マジェンタ色で図示) 環境によって歪んだ要素を避けるためにジオメトリに配置されません。」
- メッシュサイズ30のときも同じメッセージが出たが,25のときは出なかった.
- 2次要素で解析した結果は表とグラフのようになった.(30と40は一次要素のまま)
| メッシュサイズ | 要素数 | 変位 |
| 10 | 110765 | 0.000148931 |
| 20 | 27475 | 0.0001490144 |
| 21 | 27419 | 0.0001489303 |
| 23 | 19402 | 0.000148931 |
| 25 | 17792 | 0.0001489472 |
| 30 | 10050 | 0.00012982425 |
| 40 | 6912 | 0.000105412889 |
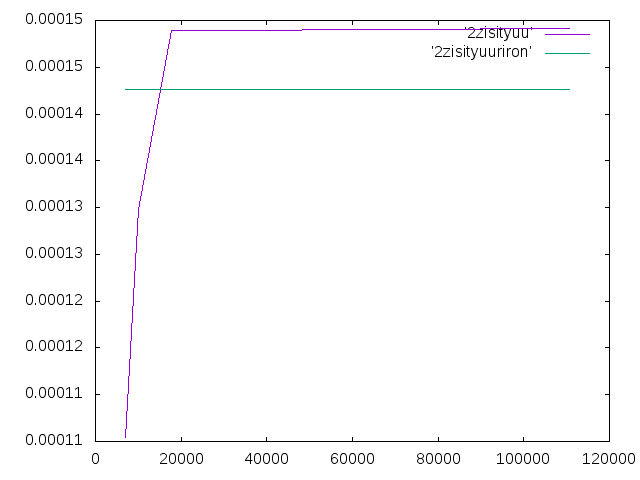
- 一番理論値に近い値の相対誤差は4.39%になった.
20/11/17†
- 床版の方も二次要素で解析した.こちらでは支柱のようなエラーは出なかった.
- しかし,要素数が大きすぎると計算時にエラーが起こった.
S> Exception user raised but not interceptee. !
! The bases are fermees. !
! Type of the exception: error !
! !
! Error during the dynamic allocation. It was not possible to allocate !
! a memory zone length 41 Mo, one exceeds the maximum limit !
! built-in with 1499 Mo and one occupies already 1469 Mo. !
! The last operation of memory deallocation made it possible to recover 0 Mo.
- メッシュサイズ25までは計算できたので,その結果を表とグラフにまとめた.
| メッシュサイズ | 要素数 | 変位 |
| 200 | 3587 | 0.0001210055 |
| 150 | 5070 | 0.0001209961 |
| 100 | 14087 | 0.000121258 |
| 80 | 16084 | 0.0001212511 |
| 70 | 18683 | 0.0001212428 |
| 60 | 21413 | 0.0001212307 |
| 50 | 54909 | 0.0001212352 |
| 40 | 63683 | 0.000121233 |
| 30 | 83221 | 0.0001212595 |
| 27 | 131296 | 0.000121299 |
| 25 | 255690 | 0.0001213208 |
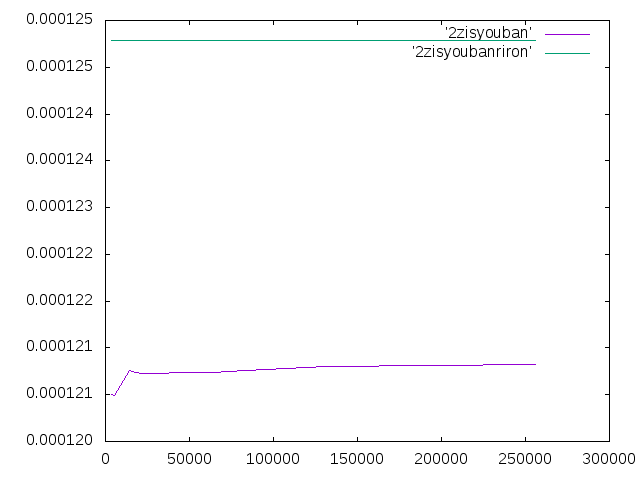
- グラフでは理論値と離れているように見えるが,一番近い値の相対誤差は-2.78%である.また,どの要素数でも変位にほとんど変化はなかった.
- Geometryで作った物体を他のファイルに移動させる方法
- 移動させたい物体を選択する→ファイル→エクスポート→STEPエクスポート→適当な場所に名前を付けて保存
- ファイル→インポート→STEPインポート→保存したものを選んで開く
20/11/18†
- 軸直交方向のヤング率(床版)を求めた.Shear Analogy Methodで,bが3000mmになるような断面で計算したら,0.7816GPaになった.
- 軸方向のヤング率を4.8704GPaとしていたが,正しくは4.7488GPaだった.等方性の単純梁のたわみの式よりヤング率が減少するとたわみは増加するので,昨日のグラフよりも理論値に近づくと考えられる.
- メッシュサイズ25で計算してみたら,より理論値に近くなった.その他の結果は表とグラフのとおりである.
| メッシュサイズ | 要素数 | 変位 |
| 25 | 255690 | 0.0001244172 |
| 27 | 131296 | 0.0001243948 |
| 40 | 63683 | 0.0001243271 |
| 60 | 21413 | 0.0001243248 |
| 100 | 14087 | 0.0001243528 |
| 20 | 3587 | 0.0001240943 |

- 理論値に一番近いところの相対誤差は-0.3%だった.遠いところでも-0.56%だった.
20/11/19†
- 支柱が降伏するときの荷重
- I=2343194.144(mm4),σ=238(MPa),l=588(mm),y=57.15(mm)のときの荷重はP=16.6(kN)
- 16.6kN=1.69tfより,支柱が降伏するときの荷重は1.69tf
- 先日の実験データのグラフ化
- 荷重と変位の関係をLibreOfficeCalc内で作成した.変位はCLTが4方向で支柱が2方向だったため,一つのグラフにまとめた.
- gnuplotでcsvファイルのグラフを作成する
- 区切りをスペースからカンマに変更:set datafile separator ","
20/11/20†
- 実験の荷重と変位,ひずみの関係のグラフを作成
- 荷重と変位の関係
- 手計算では1.69tfで降伏するという結果になったが,グラフはどの方向の変位も線形だった.支柱西側の変位に関しては線形から外れている箇所があった.
- 荷重とひずみの関係(支柱の根元)
- 内側は荷重1.8tf当たりから急激にひずみが増加している.外側は圧縮側のひずみが線形的に増加している.
- 東側上面
- 圧縮側にひずみが増加すると考えていたch11,12,13は引張側に増加した.ch11は荷重1tfまではほぼ0で,そこから圧縮側に増加したが,最終的には引張方向に増加した.また,比較的圧縮側に近いch14,ch20も引っ張り側に増加していた.
- 東側下面
- ch35〜38は圧縮側に増加していたが,しっかりとした線形ではなかった.ch41は0から動かなかった.
- 真ん中
- 少し線形から外れる点はあったが,特に問題はなかった.
- 西側上面
- 引張側は特に問題なかったが,圧縮側は0のままのものがあったり引張側に増加しているものもあった.
- 西側下面
- ch49が0からほぼ動かない.ch47,48,50が不規則な動き方をしていた.
20/11/25†
- とりあえずLibreOfficeでグラフを作成した.荷重と変位,支柱根元のひずみ,東側上面のひずみ,真ん中のひずみ,西側上面のひずみ,東側下面のひずみ,西側下面のひずみの関係をグラフで表した.
- 撮った写真はアプリでJPEG形式に変換した.
20/11/26†
- gnuplotで荷重とひずみ(支柱根元)の関係のグラフを作成した.縦軸は荷重,横軸はひずみである.
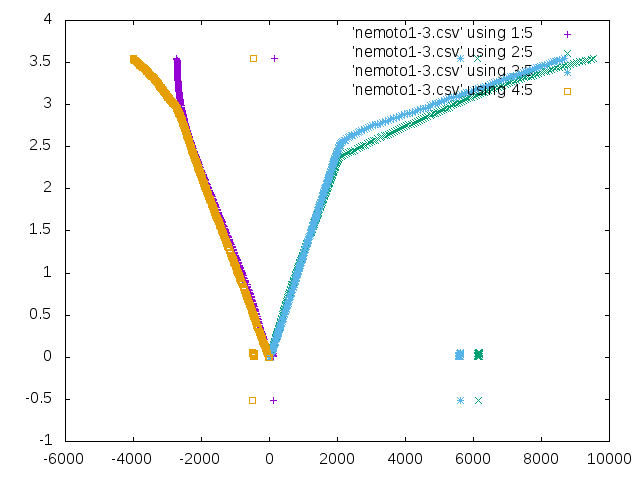
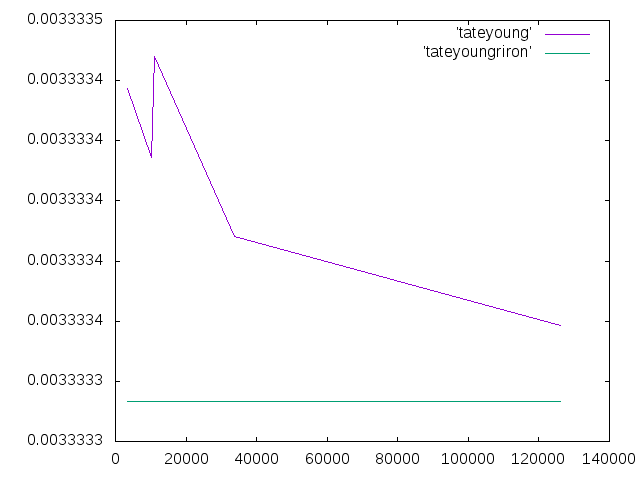
- CLTの縦ヤング率の手計算をしたら,150MPaになった.それをもとに変位を計算したところ,変位は0.0033333333mmになった.
- 確かめるため,解析も行った.繊維方向のヤング率,繊維直交方向のヤング率,縦方向のヤング率,ポアソン比,せん断弾性係数をそれぞれ記入して解析した.要素数と変位の関係はグラフのようになった.
20/11/27†
- 10倍の支柱の解析を行った.メッシュを作るとき,いつものやり方でやったら出来なかったが,及川さんに教えてもらったやり方でやったらできた.
- しかし,メッシュサイズを変えても要素数が全く変わらない.そのまま計算しても変位も全く変わらなかった.
20/11/30†
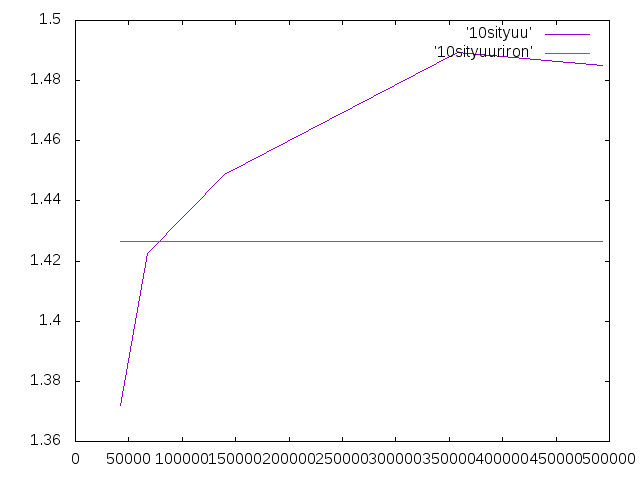
- 10倍の支柱の解析をした.Maxサイズを小さくすると要素数が増加し,minサイズを大きくすると要素数が減少することが分かった.解析結果は表とグラフのようになった.
| メッシュサイズ | 要素数 | 変位 |
| Max100 min20 | 42192 | 1.3718466667 |
| M100 m10 | 67880 | 1.4224408333 |
| M100 m4.5 | 139661 | 1.4488306757 |
| M10 m4.5 | 357844 | 1.4893606757 |
| M8 m4.5 | 493323 | 1.4849333784 |
- 全体モデル
- 全部くっついている状態,CLTの切断面を固定,ブラケットに載荷,AsterStudyのポアソン比の手前までやった.
- ポアソン比をどう決めればいいかまだわからない.
20/12/1†
- 写真をk2の/home/gakusei/zikken/cltにアップロードしました.11/24のものは20201124,12/1のものは20201201フォルダ内にあります.
20/12/2†
- ポアソン比の計算をした.構造関係メモの直交異方性材料のポアソン比のところを参考にした.
- 1/25じゃなくて1/30にしたのは,CLTメモ内のShear Analogy Methodに書いてある数値を使用したため.


20/12/3†
- せん断弾性係数の計算
- 全体モデルでの解析
- 外桁の固定面のグループをメッシュに反映させようとしたらエラーが発生した.保存せずに終了したので,明日エラーが起こる前の状態からやり直してみる.
20/12/4†
- せん断弾性係数は、どの方向も繊維方向のヤング率の1/15
- エラーが起こる前からやり直してみたが、何も問題なく反映させることができた。昨日のエラーは自分の操作ミスだった可能性が高い。
20/12/7†
- 弾性の全体モデルの解析を行った.荷重は降伏する直前の2.5tまで0.5刻みで掛けた.その結果を実験値と比較してみた.
| 荷重(t) | 変位(mm) |
| 0.5 | 1.329206 |
| 1.0 | 2.658416 |
| 1.5 | 3.98762 |
| 2.0 | 5.31683 |
| 2.5 | 6.646036 |
| 荷重(t) | 変位(mm) |
| 0.5 | 2.625 |
| 1.0 | 5.5 |
| 1.5 | 8.4 |
| 2.0 | 11.55 |
| 2.5 | 14.7 |
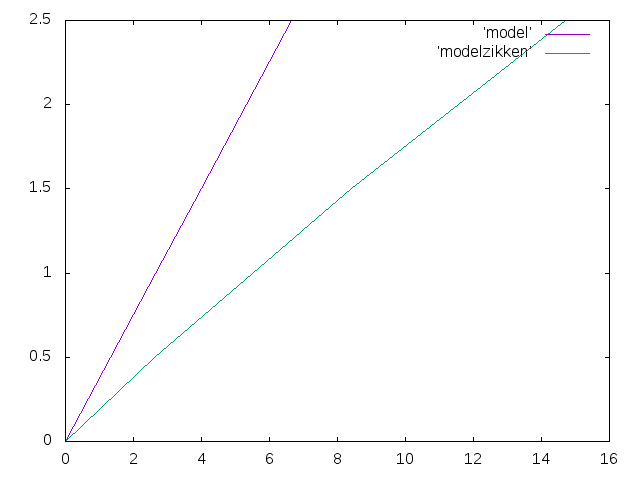
- 以下のように修正した.
- 切断面の縦方向を動けるようにした.
- 外桁部分にゴムをつけた.
- ゴムとH鋼の接触面を全面固定した.
- ゴムのヤング率:0.002GPa,ポアソン比:0.49とした.
- とりあえず荷重2.5tで解析したところ,変位は9.66262375mmとなり,実験値に近づいた.
- 次に,2次要素に直してみると,変位は12.7262142857となった.
- 2次要素ならメッシュが粗くても精度は変わらないだろうと考え,Max50,min3.2からMax100,min3.2に変えて計算したら,12.7302684211となり,ほとんど変化はなかった.
- それでも相対誤差は-13.4%ほどある.
20/12/8†
- 2次要素のメッシュサイズMax100,min3.2で0.5tから0.5刻みで計算した.結果は以下のようになった.
- 実験値は11/24のもの
| 荷重(t) | 変位(mm) |
| 0.5 | 2.5460526316 |
| 1 | 5.0921063158 |
| 1.5 | 7.6381589474 |
| 2 | 10.1842136842 |
| 2.5 | 12.7302684211 |
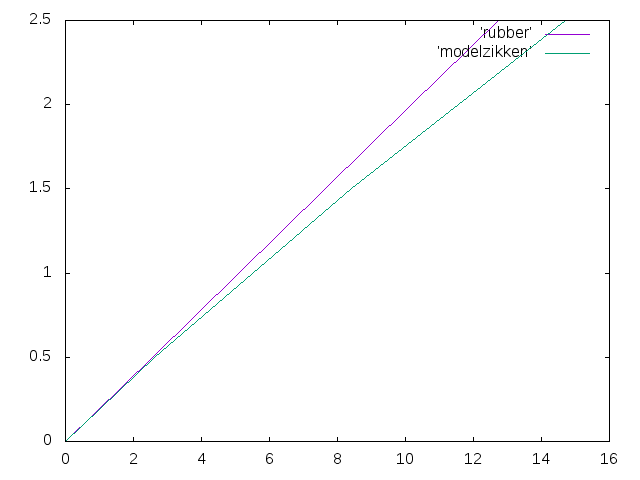
20/12/9†
- ゴムのヤング率を2MPaから100MPaに直した.ゴムが固くなった分変位は小さくなった.
- 実験でジャッキのヘッド側が回転し,斜めに荷重をかけていたので解析でもそれに対応するように設定した.しかし,変位はほとんど変わらなかった.
- 床版の真ん中の変位が実験と解析値でかなり差があったので理論値の計算をした.解析値は1.1mmほど,実験値は3.7mmくらい,理論値は5.6mmくらいになった.
20/12/16†
21/2/9†
21/2/11†
21/2/12†
卒論日誌†
| 日付 | 時間帯 | 作業時間 | 内容 | 立会 |
| 10/11 | 16:00-17:00 | 1h | ガイダンス | 後藤さん |
| 10/18 | 14:30-16:30 | 2h | 創造工房実習 | 後藤さん |
| 10/21 | 13:00-16:00 | 3h | 課題 | |
| 10/21 | 14:30-16:30 | 2h | 創造工房実習 | 後藤さん |
| 10/28 | 13:30-16:00 | 2.5h | 課題 | |
| 11/1 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 11/6 | 11:30-12:30 | 1h | 課題 | |
| 11/8 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 11/11 | 14:00-15:00 | 1h | 課題 | |
| 11/13 | 12:00-13:30 | 1h | 課題 | |
| 11/15 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 11/20 | 12:00-12:30 | 0.5h | 課題 | |
| 11/22 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 11/27 | 12:00-14:00 | 2h | 課題 | |
| 12/6 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 12/11 | 11:00-13:30 | 2.5h | 課題 | |
| 12/13 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 12/18 | 12:00-14:00 | 2h | 課題 | |
| 12/19 | 14:30-16:30 | 2h | 課題 | |
| 12/20 | 14:30-16:00 | 1.5h | 創造工房実習 | |
| 1/10 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 1/15 | 14:30-15:30 | 1h | 創造工房実習 | 後藤さん |
| 1/24 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 1/29 | 18:00-19:30 | 1.5h | 課題 | |
| 1/29 | 21:00-22:00 | 1h | 課題 | |
| 1/31 | 14:30-16:00 | 1.5h | 創造工房実習 | 後藤さん |
| 1/31 | 16:00-17:30 | 1.5h | 課題 | |
| 2/1 | 17:00-17:30 | 0.5h | 課題 | |
| 2/3 | 14:00-14:30 | 0.5h | 課題 | |
| 2/3 | 16:30-19:00 | 2.5h | 課題 | |
| 2/3 | 20:00-22:00 | 2h | 課題 | |
| 2/4 | 10:30-11:30 | 1h | 課題 | |
| 2/4 | 13:00-16:00 | 3h | 課題 | |
| 2/5 | 12:00-17:00 | 5h | 課題 | |
| 2/6 | 14:30-15:00 | 0.5h | 課題 | |
| 2/7 | 14:30-15:00 | 0.5h | 創造工房実習 | 後藤さん |
| 2/13 | 13:45-14:45 | 1h | 課題 | |
| 2/14 | 14:30-15:30 | 1h | 創造工房実習 | 後藤さん |
| 2/18 | 9:30-10:00 | 0.5h | 春休み課題 | |
| 2/26 | 14:00-16:30 | 2.5h | 春休み課題 | |
| 2/27 | 15:00-16:30 | 1.5h | 春休み課題 | |
| 3/2 | 16:45-17:45 | 1h | 春休み課題 | |
| 3/5 | 16:30-17:30 | 1h | 春休み課題 | |
| 3/7 | 16:00-18:30 | 2.5h | 春休み課題 | |
| 3/9 | 16:00-17:30 | 1.5h | 春休み課題 | |
| 3/11 | 15:30-17:30 | 2h | 春休み課題 | |
| 3/16 | 14:00-18:30 | 4.5h | 春休み課題 | |
| 3/17 | 13:00-16:00 | 3h | 春休み課題 | |
| 3/18 | 13:30-17:30 | 4h | 春休み課題 | |
| 3/19 | 14:00-17:30 | 3.5h | 春休み課題 | |
| 3/23 | 16:00-18:30 | 2.5h | 春休み課題 | |
| 3/24 | 15:00-17:30 | 2.5h | 春休み課題 | |
| 3/25 | 15:00-16:30 | 1.5h | 春休み課題 | |
| 3/26 | 16:00-17:30 | 1.5h | 春休み課題 | |
10/18の課題†
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差 | 計算者 |
| 0.5 | 394121 | 6.57938 | -1.4% | 佐藤 |
| 1 | 72278 | 6.443 | -3.4% | 吉田 |
| 2 | 11817 | 5.7382525 | -13.9% | 梅田 |
| 4 | 2862 | 4.9428 | -25.9% | 青山 |
| 8 | 897 | 4.0411725 | -39.4% | 小川 |
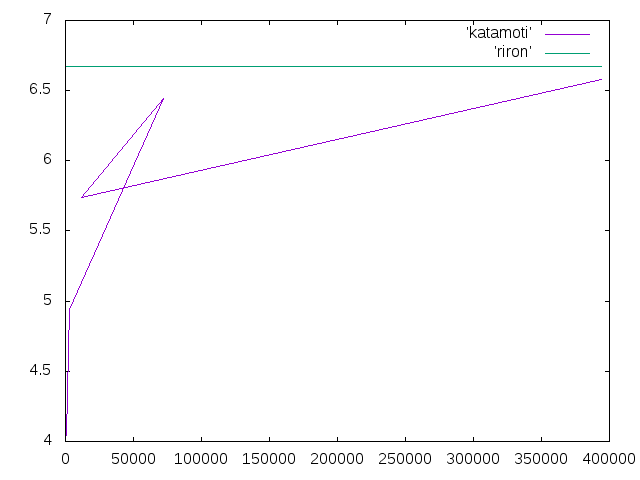
10/25の課題†
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差 | 計算者 |
| 0.5 | 394121 | 6.57938 | -1.4% | 佐藤 |
| 0.7 | 130916 | 6.4781 | -2.9% | 佐藤 |
| 0.8 | 72101 | 6.437 | -3.5% | 青山 |
| 0.9 | 71718 | 6.4314 | -3.5% | 吉田 |
| 1 | 72278 | 6.443 | -3.4% | 吉田 |
| 1.2 | 65575 | 6.443 | -3.4% | 小川 |
| 1.4 | 41096 | 6.3162 | -5.3% | 青山 |
| 1.5 | 23417 | 6.1206 | -8.2% | 梅田 |
| 1.8 | 11758 | 5.7370 | -13.98% | 梅田 |
| 2 | 11817 | 5.7382525 | -13.9% | 梅田 |
| 4 | 2862 | 4.9428 | -25.9% | 青山 |
| 8 | 897 | 4.0411725 | -39.4% | 小川 |

考察
メッシュ長さ1の時の要素数が0.9、0.8の時よりも多くなっていた。メッシュ長さが大きくなるほど相対誤差が大きくなった。
11/1の課題†
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 322687 | 0.428774714 | 2.9% | 小川 |
| 0.8 | 199968 | 0.41646 | -0.050% | 吉田 |
| 1 | 62360 | 0.416513545 | -0.037% | 梅田 |
| 1.5 | 50359 | 0.411953 | -1.134% | 青山 |
| 2 | 20526 | 0.3706311667 | -11.05% | 佐藤 |
理論値 0.416667
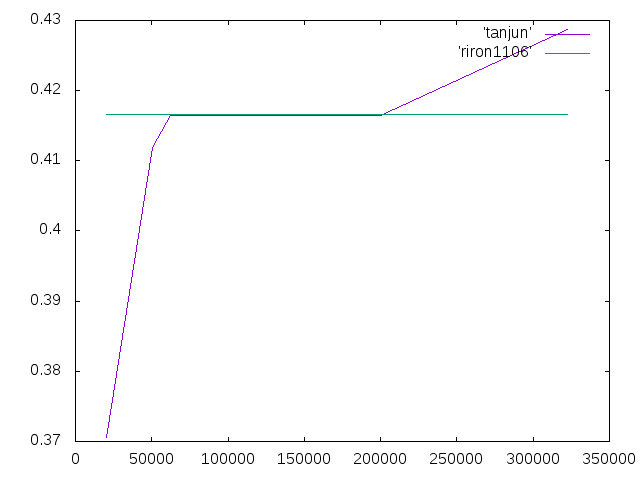
考察 メッシュを細かくするほど精度が高くなるわけではない。今回はメッシュ長さが1のとき精度が一番良かった。
11/8の課題†
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 322687 | 0.5214958571 | 6.07% | 小川 |
| 0.8 | 199968 | 0.5145437143 | 4.65% | 吉田 |
| 0.9 | 87953 | 0.5102753846 | 3.78% | 梅田 |
| 1 | 62360 | 0.505768727273 | 2.87% | 青山 |
| 1.1 | 83278 | 0.5033813636 | 2.38% | 小川 |
| 1.2 | 59515 | 0.5053267 | 2.78% | 吉田 |
| 1.3 | 57455 | 0.5038435556 | 2.47% | 青山 |
| 1.5 | 50359 | 0.50010225 | 1.71% | 梅田 |
| 1.8 | 28053 | 0.4926668571 | 0.20% | 佐藤 |
| 2 | 20526 | 0.4765718333 | -3.08% | 佐藤 |
ティモシェンコ梁 0.4916667
理論値 0.416667
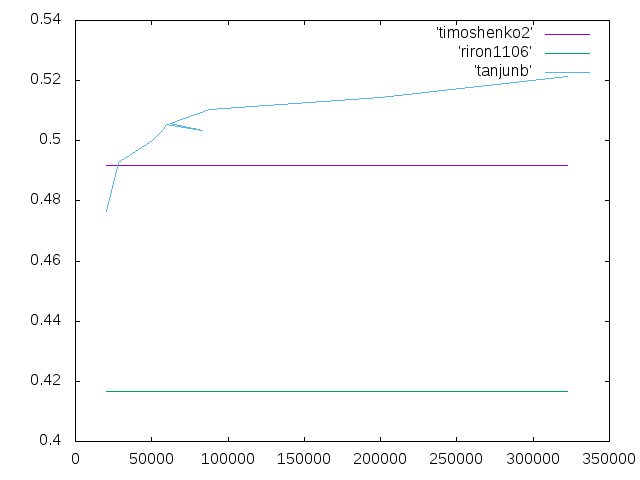
11/15の課題†
わかったこと
・自動メッシュの3次元を選択までの流れ
わからなかったこと
・スケール係数の欄がどこにあるか
・固定面の節点の選択のしかた
・エンティティの追加の欄がどこにあるか
11/22の課題†
| 拡大係数 | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.3 | 57431 | 6.422525 | -3.7% | 全員 |
| 0.4 | 23349 | 6.26413 | -6.0% | 佐藤 |
| 0.5 | 13741 | 6.03154 | -9.5% | 小川 |
| 0.6 | 7257 | 5.91187 | -11.3% | 梅田 |
| 0.7 | 4245 | 5.5716725 | -16.4% | 吉田 |
| 0.8 | 3657 | 5.5734 | -16.4% | 青山 |
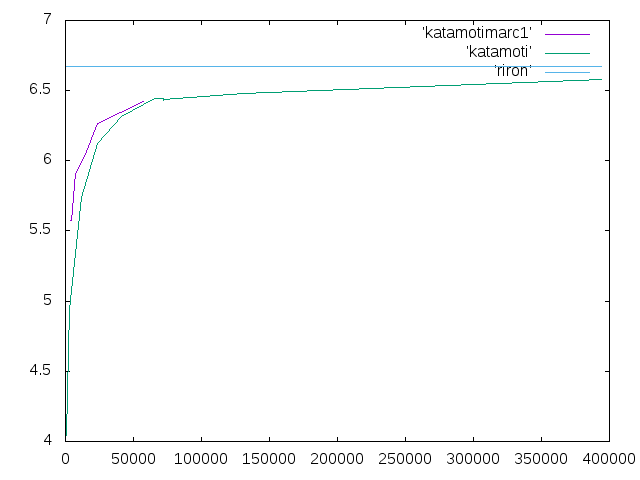
12/6の課題†
| 拡大係数 | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.8 | 122515 | 6.91749 | 2.6% | 吉田 |
| 1 | 65490 | 6.8877 | 2.2% | 梅田 |
| 1.2 | 36693 | 6.8519225 | 1.6% | 梅田 |
| 1.4 | 23341 | 6.8117175 | 1.0% | 吉田 |
| 1.6 | 15371 | 6.6336 | -1.6% | 小川 |
| 1.8 | 12480 | 6.74258 | 0.014% | 佐藤 |
| 2 | 8589 | 6.66499 | -0.011% | 梅田 |
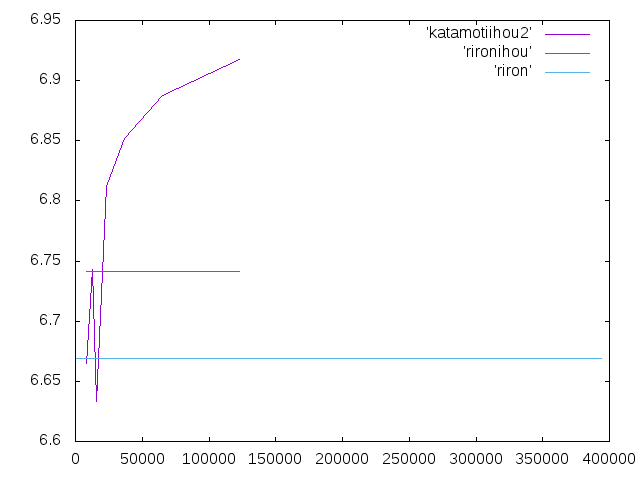
節点数で荷重を割るときに精度を上げていれば変位が下がらずに済んだと思う。
有効数字
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)



