中村の卒論日誌

卒論日誌†

課題１・２(5/28)　円筒のばね定数kを高さを変えて計算する†

• P 100N　
• 半径 50mm　
• 厚さ 0.1mm
• E 5000MPa
• 高さ 30mm、200mm
• γ 0.3

k=EA/h、k=P/Δhの式を比較して相対誤差を求める

課題３（5/30）螺旋折円筒のばね定数解析†

• ６角
• P 1000N
• 半径 30mm
• 高さ 40mm 線形解析k=9.8/0.2374=41.28

課題４（6/11）高さ、半径、荷重、角の数を変えてばね定数を計算する†

• ６角
• P 2000N
• 半径 30mm
• 高さ 40mm

課題５（6/25）円筒の高さのみを変えてばね定数を比較する†

• 6角
• P 1000N
• 半径　60mm
• 高さ　10-100mm

• (7/12)10mm、20mmと高さが小さいとジオメトリ作成する際にどれがどの線なのか分かりづらく中々上手くいかない
• (7/15)10mm20mm30mmを110mm120mm130mmにしてみようと思ったが高さが110mmの時点で回転角を求められなくなった。

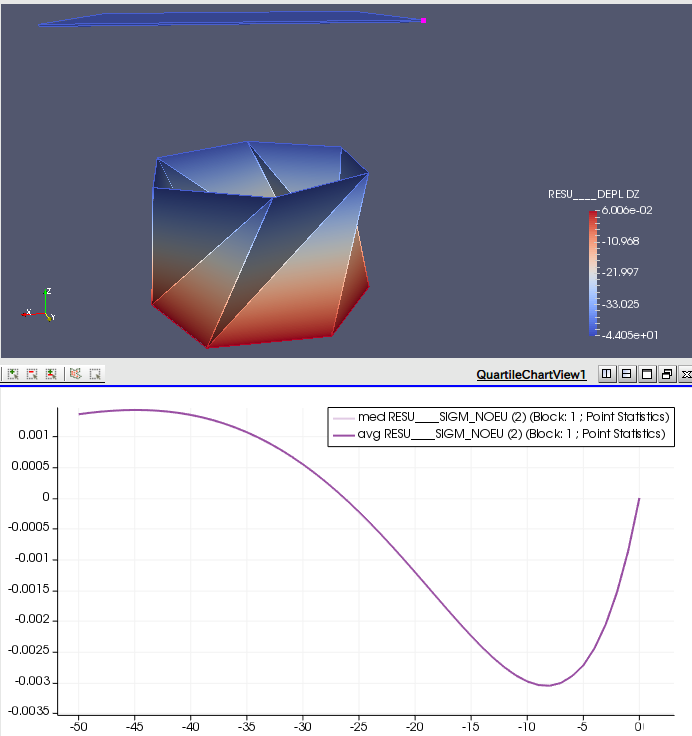
そもそも荷重が大きすぎてひずみが高さを越えてしまっているため、次回は荷重を小さくしてやってみる。(1000Nから100N？)

オープンキャンパス準備(7/12)†

サルバティコ体験学習用図面よりジオメトリを作成した。

• 主材、水平材の一段目まで作成できた(7/12)
• 次は二段目、角度

• やはり角度が分からない。とりあえず必要な部材のボックスだけ全て作成した(7/15)
• 作成完了（7/23）

課題６(7/15)ヒンジでない時のばね定数†

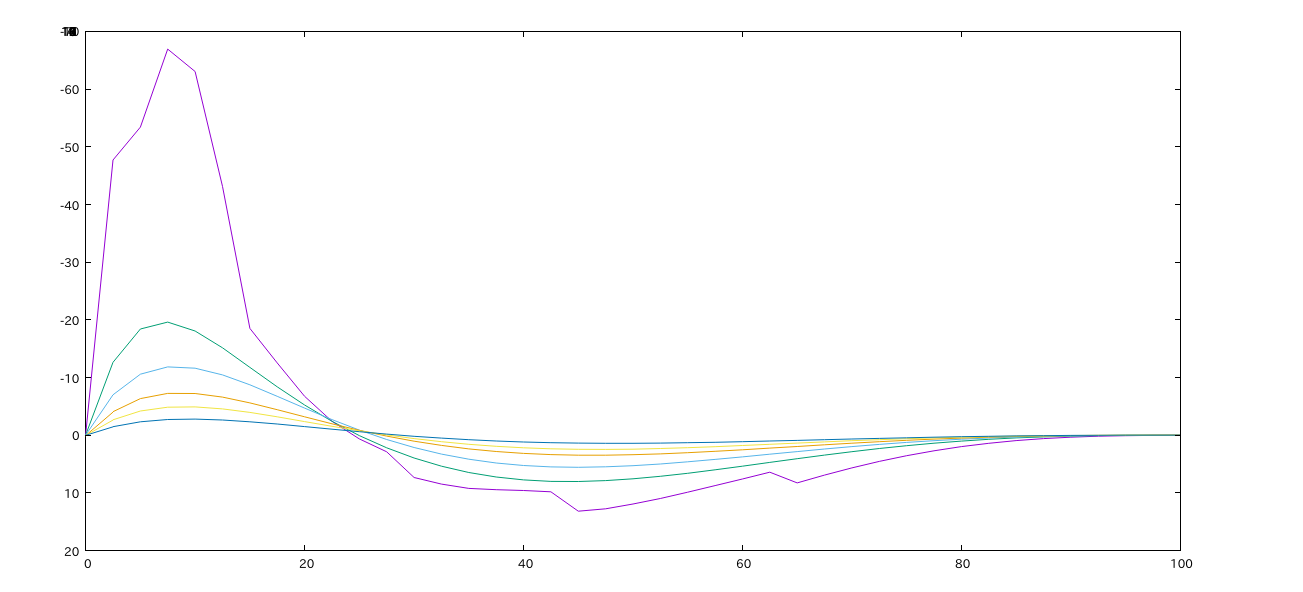
螺旋円筒の角がヒンジになっていない時のばね定数Aを、ヒンジになっている時のものBと比較する。

課題７(9/2)†

荷重500Nとしてまた新たにデータを集めていく。荷重1000Nでのこれまでのデータからするとヒンジでない時のばね定数の方がヒンジである時よりも大きい。荷重500Nでも同じような結果となるか、また荷重、高さ以外にも今回は半径を変化させた場合のデータも集積していく。

課題８(10/15)†

11/9†

• salome2017で頂点に変な荷重がかかってしまう問題がsalome2016で解決されるかどうか
• また５角、４角など角数変えた場合の荷重の変化など（変位制御）
• 2016で解決されるようであれば今後は2016を使っていく
  • 2016でメッシュ作成する際、3Dに設定ができない。厚さを変えても3Dが選択できない。後日遠藤さんに教えてもらいたいがとりあえず６角、５角、４角のジオメトリで面まで作成している状態
  • asterstudyのエラー「拠点が閉鎖されています」とは？
• (11/16)salome2016のメッシュで3Dが選択できなかった問題は、ジオメトリ→新しいエンティティ→ビルド→ソリッドより全てのオブジェクトを選択して（１つのソリッドを作成のチェックは外す）適用してから、グループの作成→固定線載荷線、、というように今までどおり進めていけば解決された。（中身が空になっていた為3Dにならなかった？）

11/16†

• 用途のネタ随時探す(仮囲い、医療機器など？)

11/30†

• salome2016での非線形解析のcommファイル http://www.str.ce.akita-u.ac.jp/~gotouhan/j2018/nakamura/hisennkei.comm
• 非線形解析でのグラフ
• 5角、4角もやっていく。また、載荷をずっと内側に線載荷でやっていたので、面載荷、外側に線載荷した場合との違いも考えていく。(12/5)

12/7†

• commの内容（英語の意味とか？）理解しておく。
• このNON-LINEは非線形を表す？

1/11†

• 角の数多いほど折り畳まれるのに必要な荷重が少なく済むことが分かったが、7角、8角・・・とどこかで傾向が変わるポイントがあるはずなので（円柱は折り畳まれないことから）、また角増やしながらいろいろやってみる。
• 材料はこのまま紙でいく
• 卒論のスライドには荷重変位曲線に実際どのくらい折り畳まれているかの図を貼る、またアニメーションも貼りたい
• ６角は何に使える？４角は何に使える？傾向が分かったら実際どう使えるかまで考える
• 線形解析と非線形解析の違い説明できるように

1/12†

• とりあえず７角、１０角、１２角のジオメトリまでは作成したが、どれもメッシュ切る際に計算が全く進まなくなる。メッシュが細かすぎる？でも６角までと同じメッシュの大きさにしているので原因が謎。たまにこうゆうことがある。

1/15†

• 8角は何事もなくParavisまでいけた。7角も新しいジオメトリ作ったらできた。
• 12角までグラフ作成したがまだ荷重小さくなり続けている。次18角(1/16)

1/18†

• スライドにアニメーション貼ってpdfにしても再生される？→再生されなかった
• 多分どんどん角数増やしていっても折り畳まれるのに必要な荷重は減っていく。円筒にはなりきらないかも？どんどん０に近づいていく（12角現在）
• 紙だと手を離す（荷重を０にする）と折り目の反発力によって戻る
• 三次元プロットにする（荷重、変位、角数）

1/22†

• 5mm刻みで値とってグラフ作ることにしたが4角のを100ステップ（他のは全て200ステップ）にしてしまっていた。200に直そうとした（2.5刻みにしようとしたがステップ数は整数にしかできなかった為）があまりにもエラーが続くので明日またジオメトリから作りなおす。

1/23†

• 何度か作りなおしたが4角がどうしてもきれいに折り畳まれない。(回転角は合ってる) とりあえず5から9角で進める。
• 単体のデータの三次元プロットはできるが複数のデータをまとめたプロットが分からない
• パッと見奇数角偶数角に大きな違いはなさそう
• 全ての角の0mm、10mm、40mm、70mm、100mmのスクショ撮った

1/25†

• ４角から８角、１２角で三次元プロット（変位、荷重、角数）した。４角は２３日のもので大丈夫であった。角の数や材料によって座屈する高さがあるらしい。今回の半径80高さ100の場合は４角以下は座屈する。
• ９角が何故か７角８角より荷重大きくなってしまうデータになっていたので９角除外
• 奇数と偶数での違いはなし。面が全て三角であり、その面の中で解決（？）するのでこの間の中間発表で言われたような現象はおこらないらしい。
• 座屈しているので４角のみカクカクした線になっている

1/27†

• 三次元じゃない方が分かりやすい気もする

2/6†

• 13:00から発表練習

最新の100件