構造力学IIオンライン授業用テキスト
第12回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
前回、
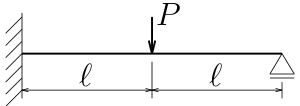
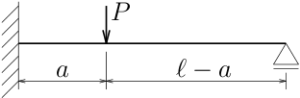
図のような1次不静定で中央に集中外力を受ける梁のたわみを、
$-EIv''''(z)+q(z)=0$を4回積分して求めた。
$0\le z\le\ell$と$\ell\le z \le 2\ell$の
各領域ごとに、積分定数が4つずつの、計8個の未知数を連立させて解かなけれは
ならないので、なかなか計算量が多くなり、解くのが大変だったと思う。
一般に不静定の問題は解くのが大変なので、
物理的考察により工夫して、
少しでも解くのを簡単にするための各種の「便法」がたくさんある。
今回は、その中で比較的 使いやすい
「不静定反力を外力に置き換えて解く」方法を紹介する。
この他にも各種の便法があるが、
重ね合わせの原理なども、
割と簡単に解け、応用の効く解き方なので、
興味のある人または院試や就職試験の対策をしたい人は、覚えておいても
いいだろう。
コンピューターで簡単に構造解析できなかった時代には、
手計算だけで構造力学の問題を解くために、
多種多様な解法が考案され、私が大学生の頃は、
そうした多種多様な方法をたくさんやらされた。
しかし、梁の解法の本質は、
梁の支配方程式
$-EIv''''(z)+q(z)=0$を
境界値問題として解けるということだと思うので、
この授業では、様々な解法を網羅的に教えるということはしない。
例えば、$M(z)=-EIv''(z)$を導くまでの
第1回から
第5回や
$-EIv''''(z)+q(z)=0$を導くまでの
第9回といった
梁理論の導出の過程を全くやらずに
ブラックボックスにしておいて、
こうした公式各種はすべて、そういう「公式」として
暗記してもらい、そこで空いた時間を、
梁の解法の各種の便法
（弾性荷重法、三連モーメント、たわみ角法、カスティリアーの定理）を
教えるために費やすというやり方もあり得るが、
私の価値観としては、大学生は、
理論の導出もある程度トレースできるようになってほしい。
何か1つでも、理論体系を自力でトレースできることを体験していれば、
自分にとって専門外でブラックボックスな理論体系でも、
こんな感じで導出されているんだろうなという
想像力を養うことができる。
こうした想像力があるかないかは、とても大きな違いだと私は感じる。
初等梁理論は、
みなさんでも十分に、その導出過程を理解できる理論体系だと思うので、
ぜひ、自力で、導出をトレースできたという感動を体験してほしい。
不静定梁は、力のつりあいから反力を求めることができないが、
不静定反力のいくつかを外力に置き換えてやって、
静定構造にしてやれば、ひとまず、反力や曲げモーメントを力のつりあいから
求めることはできる。
外力に置き換えた反力（不静定外力と呼んでおく）は、ひとまず$Q$とかの
記号で表しておいて、それを用いて$M(z)$や$v(z)$を求めて、
最後に、不静定外力の載荷点で、実際には拘束されているからたわみがゼロといった
拘束条件を用いて、不静定外力$Q$を求めればよい。
図のような1次不静定の梁について、このやり方で解いてみる。
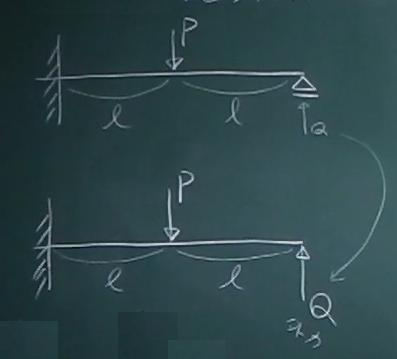
図の不静定梁は、反力が4つの1次不静定梁であるから、
適当な反力1つをとり除いて、その反力に対応する拘束を外してやれば、
静定梁（単純梁か片持ち梁）に置き換えることができる。
図の不静定梁の場合、左端のモーメント反力をモーメント外力に置き換えて
単純梁にすることもできるし、右端の鉛直反力を外力に置き換えて片持ち梁に
することもできる。
今回は、後者のやり方をやってみる。
右端のローラー支承に作用している反力を、上向きに$Q$と仮定し、
これが、片持ち梁の右端に作用していることにする。
その代わり、右端の鉛直方向の拘束は外して自由端とする。
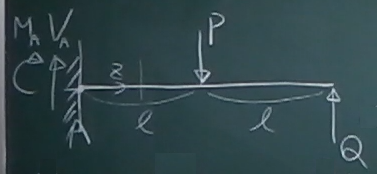左端のモーメント反力を$M_{A}$, 鉛直反力を$V_{A}$として、
力のつりあいから、まずこれらを求める。
$\sum\downarrow =-V_{A}+P-Q=0$
$\sum\circlearrowleft=-M_{A}-P\cdot\ell+Q\cdot 2\ell =0$
$V_{A}=P-Q$
$M_{A}=2Q\ell-P\ell$
次に$M(z)$を求めるが、途中に集中外力$P$があるので、
$0\le z\le\ell$と$\ell\le z\le 2\ell$に場合分けする。
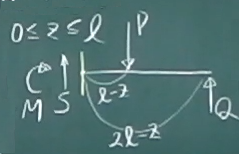まず、$0\le z\le\ell$の任意断面で梁を2つのピースに切り離し、
どちらかのピースを取り出してつりあいを考えればいいが、
今回は右側のピースを取り出す。
$\sum\downarrow =-S+P-Q=0$
$\sum_{z}\circlearrowleft=-M-P(\ell-z)+Q(2\ell-z)=0$
切断点($z$点)まわりのモーメントの腕の長さの考えなど、忘れている人は、
構造力学I第5回を参照。
$S(z)=P-Q$
$M(z)=(P-Q)z+2Q\ell-P\ell$
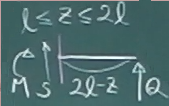次に、$\ell\le z\le 2\ell$の任意断面で梁を2つのピースに切り離し、
どちらかのピースを取り出してつりあいを考えればいいが、
今回は右側のピースを取り出す。
$\sum\downarrow =-S-Q=0$
$\sum_{z}\circlearrowleft=-M+Q(2\ell-z)=0$
$S(z)=-Q$
$M(z)=Q(2\ell-z)$
$M(z)$が求まったので、それぞれの領域について、
$M(z)=-EIv''(z)$を2回積分して$v(z)$を求める。
第8回の要領で、
$0\le z\le\ell$の左半分のたわみを$v_{左}$と書いて、
$\ell\le z\le 2\ell$の右半分のたわみを$v_{右}$と書くことにする。
ここではわかりやすく「左」「右」の添字を使っているが、
みなさんが小テストなどで手計算する際は、めんどくさいんで、
$v_{1}, v_{2}$とか、好きなように。
度々 言っているが、記号の書き方は便宜上のもので、本質ではない。
まずは $0\le z\le\ell$について。
$-EIv_{左}''=(P-Q)z+2Q\ell-P\ell$
$EIv_{左}''=(Q-P)z+P\ell-2Q\ell$
$EIv_{左}'=\frac{Q-P}{2}z^{2}+\ell(P-2Q)z+A$
$EIv_{左}=\frac{Q-P}{6}z^{3}+\frac{\ell(P-2Q)}{2}z^{2}+Az+B$
次に、$\ell \le z\le 2\ell$について。
$-EIv_{右}''=Q(2\ell-z)$
$EIv_{右}''=Q(z-2\ell)$
$EIv_{右}'=\frac{Q}{2}z^{2}-2Q\ell z+C$
$EIv_{右}=\frac{Q}{6}z^{3}-Q\ell z^{2}+Cz+D$
今 解いている静定梁について、
第8回の要領で
境界条件や連続条件を考えていく。
まず境界条件は、左端が固定端だから、左端($z=0)$でたわみとたわみ角がゼロ。
$v_{左}(0)=0$
$v_{左}'(0)=0$
連続条件は、集中荷重載荷点($z=\ell$)で梁が切れたり折れたりしないから、
$v_{左}(\ell)=v_{右}(\ell)$
$v_{左}'(\ell)=v_{右}'(\ell)$
未知数は、積分定数$A, B, C, D$の4つと考えれば、上の4つの条件式を使って、
$A, B, C, D$を$P, Q$で表すことができる。
$v_{左}(0)=0$より
$EIv_{左}(0)=B=0$
$v_{左}'(0)=0$より
$EIv_{左}'(0)=A=0$
$EIv_{左}'(\ell)=EIv_{右}'(\ell)$より
$\frac{Q-P}{2}\ell^{2}+(P-2Q\ell)\ell^{2}=\frac{Q}{2}\ell^{2}-2Q\ell^{2}+C$
$C=\frac{P\ell^{2}}{2}$
$EIv_{左}(\ell)=EIv_{右}(\ell)$と
$C=\frac{P\ell^{2}}{2}$
より
$\frac{Q-P}{6}\ell^{3}+\frac{P-2Q}{2}\ell^{3}=\frac{Q}{6}\ell^{3}-Q\ell^{3}+
\frac{P\ell^{3}}{2}+D$
$D=-\frac{P\ell^{3}}{6}$
$A, B, C, D$は求まったので、こららを$v_{左}$, $v_{右}$の式に
代入すれば、外力$P$と$Q$を受ける静定梁のたわみを$P, Q$で表すことができる。
が、それは省略する。
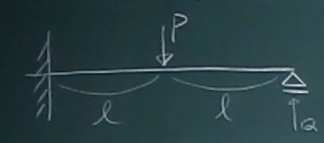さて、解きたかったのは図のような右端の鉛直変位が拘束された不静定梁であるが、
この元の梁では、
右端のたわみはないので、
$v_{右}(2\ell)=0$
の拘束条件が使える。
これを用いて、$Q$を$P$で表してやる。
$EIv_{右}(2\ell)=0$
と
$C=\frac{P\ell^{2}}{2}$
と
$D=-\frac{P\ell^{3}}{6}$
より
$\frac{8}{6}Q\ell^{3}-4Q\ell^{3}+P\ell^{3}-\frac{P\ell^{3}}{6}=0$
$Q=\frac{5}{16}P$
さて、これで積分定数$A, B, C, D$と不静定外力$Q$が求まったので、
これらを$v_{左}$, $v_{右}$の式に代入すれば、不静定梁のたわみが求まる。
$
v(z)=
\begin{cases}
\frac{P}{96EI}(-11z^{3}+18\ell z^{2}) &\;\;\;\;(0\le z\le \ell)\\
\ \\
\frac{P}{96EI}(5z^{3}-30\ell z^{2}+48\ell^{2}z-16\ell^{3}) &\;\;\;\;
(\ell\le z\le 2\ell)\\
\end{cases}
$
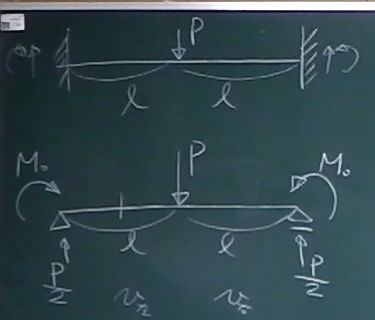図の不静定梁の2つのモーメント反力を、
図(下)のように対称な2つの不静定モーメント外力$M_{0}$に置き換えて
たわみを求めよ。
曲げ剛性は$EI$とする。
答えはここ。
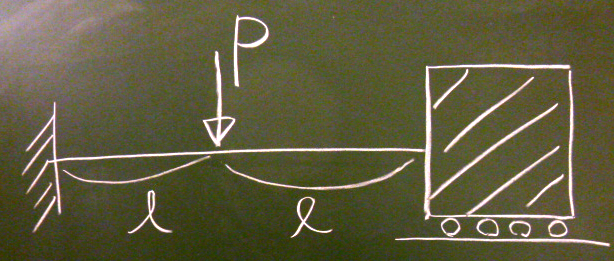厳密に考えると、これは反力が6つで3次不静定だから、
不静定外力も3つにしないと静定構造にならないが、
軸方向の外力のない梁の問題では、水平反力はゼロの前提で考えてよい。
もちろん、
もし、本当に両端固定のこういう構造を作って、真ん中を押したら、
水平反力が発生しないわけはないから、
そういう意味では、片側の固定端の下にローラーがついていて、
水平変位は拘束されていない問題として出題した方が正確かもしれない。
その他、計算過程の解答は特にないが、
前回の例題など（あるいは、上の問題を今度は違う反力を外力に置き換えて）、
答えのわかる不静定梁の問題について、
適当な不静定反力を外力に置き換えて、解いてみよう。
$-EIv''''+q=0$を積分して解いた答えはここ。
2022年度小テスト：
小テスト230118
2021年度小テスト：
問,
解答
2020年度小テスト：
問1-2,
解答
メモ:
