[Googleで検索] [ウィキペディア] [IT用語辞典] [秋田大学蔵書検索システム] [ シラバス ] (土木環境工学実験) (情報処理の技法) (後藤資料)

構造力学(準備開始)
不静定梁のたわみ(練習問題)

注意： このページの数式は、 MathJaxを使って書いてます。 数式部分がおかしい場合は、更新ボタンをクリックすると 改善するかも知れません。 太文字のギリシャ文字($\mathbf{\sigma}$など)が、 太文字になっていない($\sigma$)かもしれません。 印刷版で確認して下さい。 その他、おかしい記述があると思ったら、 メールなどで指摘して下さい。

構造力学ウェブテキストへ戻る

問1

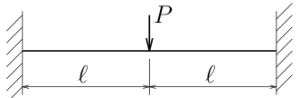./png/ryouko.png 図のような両端固定で中央に集中荷重を受ける不静定梁について、 梁の支配微分方程式を使ってたわみを求めてみる。 梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。 便宜上、 $0<z <\ell $ の左半分のたわみを$v_{左}$と書いて、 $\ell <z<2\ell $ の右半分のたわみを$v_{右}$と書くことにし、 $\frac{d}{dz}$の微分を$'$で表すと、分布外力がないので、

$EIv''''=0\;\;\;\;(0<z <\ell )$
$EIv''''=0\;\;\;\;(\ell <z<2\ell )$

それぞれ$z$について 4回積分してみると、

$0<z <\ell $ について
$EIv''''_{左}=0$
$EIv'''_{左}=A$
$EIv''_{左}=Az+B$
$EIv'_{左}=\frac{A}{2}z^{2}+Bz+C$
$EIv_{左}=\frac{A}{6}z^{3}+\frac{B}{2}z^{2}+Cz+D$

$\ell <z<2\ell $ について
$EIv''''_{右}=0$
$EIv'''_{右}=F$
$EIv''_{右}=Fz+G$
$EIv'_{右}=\frac{F}{2}z^{2}+Gz+H$
$EIv_{右}=\frac{F}{6}z^{3}+\frac{G}{2}z^{2}+Hz+J$
となる。
まず境界条件として使えるのは、 両端でたわみとたわみ角が0つまり
$v_{左}(0)=0$, $v'_{左}(0)=0$, $v_{右}(2\ell )=0$, $v'_{右}(2\ell )=0$
の4つの条件で、これらの条件から、
$C=0$
$D=0$
$H=-2F\ell^{2}-2\ell G$
$J=\frac{8}{3}F\ell^{3}+2G\ell^{2}$
となる。

左右対称による対称条件として使えるのは、 中央の集中荷重載荷部で、たわみ角が$0$つまり、
$v'_{左}(\ell )=0$から
$\frac{A}{2}\ell^{2}+B\ell =0$
あと、両端の支点反力は左右対称だから$\frac{P}{2}$になるから、 せん断力も$S_{左}=-S_{右}=\frac{P}{2}$. もう少しちゃんと考えたければ、 中央の集中荷重載荷部の微小部分を図のように薄くスライスして 切り取ってみると、

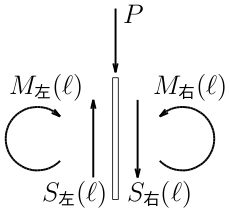./png/suraisupl.png 鉛直方向の力のつりあい(下+): $-S_{左}(\ell )+P+S_{右}(\ell )=0$
となる。 左右対称だから$S_{左}(\ell )=-S_{右}(\ell )$となる。よって、 $S_{左}(\ell )=\frac{P}{2}, S_{右}(\ell )=-\frac{P}{2}$となる。 また、このスライスの厚さが0だとしてモーメントの つりあいを考えると
モーメントのつりあい(左まわり正): $-M_{左}(\ell )+M_{右}(\ell )=0$
となる。 せん断力は$S=-EIv'''$と曲げモーメントは$M=-EIv''$とそれぞれ関係づけられるから 、 これらのつりあい条件は、
$S_{左}(\ell )=-EIv'''_{左}(\ell )=\frac{P}{2}$
$S_{右}(\ell )=-EIv'''_{右}(\ell )=-\frac{P}{2}$
$-(-EIv''_{左}(\ell ))+(-EIv''_{右}(\ell ))=0$
と書けるが、 これらの式を用いて
$A=-\frac{P}{2}$
$F=\frac{P}{2}$
$B=\frac{P\ell }{4}$
$G=-\frac{3}{4}P\ell $
$H=\frac{P\ell^{2}}{2}$
$J=-\frac{P\ell^{3}}{6}$
が得られる。
よって、たわみは
$v_{左}=\frac{P}{24EI}(-2z^{3}+3\ell z^{2}) \;\;\;\;(0< z<\ell )$
$v_{右}=\frac{P}{24EI}(2z^{3}-9\ell z^{2}+12\ell^{2}z-4\ell^{3}) \;\;\;\;(\ell < z<2\ell )$

せん断力は、
$S_{左}(z)=-EIv_{左}'''(z)=-A=\frac{P}{2} \;\;\;\;(0<z <\ell )$
$S_{右}(z)=-EIv_{右}'''(z)=-F=-\frac{P}{2} \;\;\;\;(\ell <z<2\ell )$

曲げモーメントは、
$M_{左}(z)=-EIv_{左}''(z)=-Az-B=\frac{P}{4}(2z-\ell ) \;\;\;\;(0<z <\ell )$
$M_{右}(z)=-EIv_{右}''(z)=-Fz-G=\frac{P}{4}(-2z+3\ell ) \;\;\;\;(\ell <z<2\ell )$
$M_{左}(\ell )=M_{右}(\ell )=\frac{P\ell }{4}$

./png/ryouko.png

./png/ryoukosmv.png

問2

左端から右端まで等分布荷重が作用する問題は、 場合分けしなくていいから積分定数が4つですみ、 両端の境界条件だけで解けてしまう。 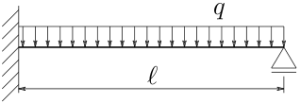./png/ukosahitou.png 梁の支配微分方程式は$-EIv''''+q=0$だから、
$EIv''''=q$
$EIv'''=qz+A$
$EIv''=\frac{q}{2}z^{2}+Az+B$
$EIv'=\frac{q}{6}z^{3}+\frac{A}{2}z^{2}+Bz+C$
$EIv=\frac{q}{24}z^{4}+\frac{A}{6}z^{3}+\frac{B}{2}z^{2}+Cz+D$
境界条件は左端でたわみとたわみ角が$0$, 右端でたわみと曲げモーメントが$0$つまり、
$v(0)=0, v'(0)=0, v(\ell )=0, v''(\ell )=0$
これらより、
$A=-\frac{5}{8}q\ell $
$B=\frac{q\ell^{2}}{8}$
よってたわみは
$v=\frac{q}{48EI}(2z^{4}-5\ell z^{3}+3\ell^{2}z^{2})$
せん断力は
$S=-EIv'''=-qz-A=\frac{q}{8}(-8z+5\ell )$
曲げモーメントは
$M=-EIv''=-\frac{q}{2}z^{2}-Az-B=\frac{q}{8}(-4z^{2}+5\ell z-\ell^{2})$

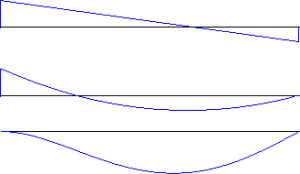
./png/kohintousmv.png

問3

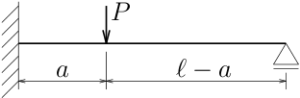./png/kotehina.png 図のような左端固定、右端ローラー支承で集中荷重を受ける梁の 左端を原点とし、梁軸に沿って右向きに$z$軸を取り、 たわみ$v(z)$ を$z$の関数として求めよ。

解答

便宜上、 $0<z <a$ の左側のたわみを$v_{左}$と書いて、 $a<z<\ell $ の右側のたわみを$v_{右}$と書くことにし、 $\frac{d}{dz}$の微分を$'$で表すと、分布外力がないので、 $0<z<a$について
$EIv''''_{左}=0$
$EIv'''_{左}=A$
$EIv''_{左}=Az+B$
$EIv'_{左}=\frac{A}{2}z^{2}+Bz+C$
$EIv_{左}=\frac{A}{6}z^{3}+\frac{B}{2}z^{2}+Cz+D$

$a<z<\ell $について
$EIv''''_{右}=0$
$EIv'''_{右}=F$
$EIv''_{右}=Fz+G$
$EIv'_{右}=\frac{F}{2}z^{2}+Gz+H$
$EIv_{右}=\frac{F}{6}z^{3}+\frac{G}{2}z^{2}+Hz+J$

境界条件

左端の境界条件は固定端だからたわみとたわみ角が$0$, つまり
$v_{左}(0)=0, v_{左}'(0)=0$より
$D=0, C=0$
右端の境界条件はローラー支承だからたわみとモーメントが$0$, つまり
$v_{右}(\ell )=0, v_{右}''(\ell )=0$より
$G=-F\ell $
$J=\frac{F}{3}\ell^{3}-H\ell $
$EIv''_{右}=Fz-F\ell $
$EIv'_{右}=\frac{F}{2}z^{2}-F\ell z+H$
$EIv_{右}=\frac{F}{6}z^{3}-\frac{F\ell }{2}z^{2}+Hz+\frac{F}{3}\ell^{3}-H\ell $

連続条件

集中荷重載荷部($z=a$)での連続条件は、たわみとたわみ角が連続、つまり
$v_{左}(a)=v_{右}(a)$
$v_{左}'(a)=v_{右}'(a)$
これらを用いて式を整理すると以下の2式が得られる。
$a^{2}A+2aB+(2\ell a-a^{2})F=2H$
$a^{3}A+3a^{2}B-(a^{3}-3\ell a^{2}+2\ell^{3})F+6(\ell -a)H=0$
$H$を消去しておくと、
$(-2a^{3}+3\ell a^{2})A+(-3a^{2}+6\ell a)B +(2a^{3}-6\ell a^{2}+6\ell^{2}a-2\ell^{3})F=0$

つりあい条件

$z=a$の部分の微小なスライスを切り出してつりあい条件を考えると、 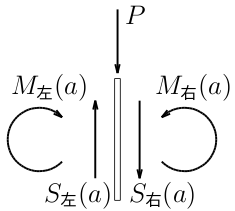./png/suraisupa.png 鉛直方向の力のつりあい(下+): $-S_{左}(a)+P+S_{右}(a)=0$
となる。また、このスライスの厚さが0だとしてモーメントの つりあいを考えると
モーメントのつりあい(左まわり正): $-M_{左}(a)+M_{右}(a)=0$
となる。 せん断力は$S=-EIv'''$と曲げモーメントは$M=-EIv''$とそれぞれ関係づけられるから 、 これらのつりあい条件は、
$-(-EIv'''_{左}(a))+P+(-EIv'''_{右}(a))=0$
$-(-EIv''_{左}(a))+(-EIv''_{右}(a))=0$
これらより
$A=F-P$
$aA+B+(\ell -a)F=0$
が得られる。$A$を消去すると、
$B=a-\ell F$

連続条件のところで$A$と$B$と$F$だけで表した式
$(-2a^{3}+3\ell a^{2})A+(-3a^{2}+6\ell a)B +(2a^{3}-6\ell a^{2}+6\ell^{2}a-2\ell^{3})F=0$
に $A=F-P$と $B=a-\ell F$を代入して$F$を求めると、
$F=\frac{Pa^{2}}{2\ell^{3}}(3\ell -a)$
後は順次 代入していって
$G=\frac{Pa^{2}}{2\ell^{2}}(a-3\ell )$
$B=\frac{P}{2\ell^{2}}(2\ell^{2}a-3\ell a^{2}+a^{3})$
$A=\frac{P}{2\ell^{3}}(3\ell a^{2}-a^{3}-2\ell^{3})$
$H=\frac{a^{2}}{2}$
$J=-\frac{a^{3}}{6}$
よってたわみは、 $v_{左}(z)=\frac{P(\ell -a)}{12\ell^{3}EI} \{(a^{2}-2\ell a -2\ell^{2})z^3+(6\ell^2 a-3\ell a^{2})z^{2}\} \;\;\;\; (0<z<a)$
$v_{右}(z)=\frac{Pa^{2}}{12\ell^{3}EI} \{(3\ell -a)z^{3}-3\ell (3\ell -a)z^{2}+6\ell^{3}z-2\ell^{3}a\} \;\;\;\; (a<z<\ell )$
せん断力は、
$S_{左}=-EIv_{左}'''=-A=\frac{P}{2\ell^{3}}(a^{3}-3\ell a^{2}+2\ell^{3}) \;\;\;\; (0<z<a)$
$S_{右}=-EIv_{右}'''=-F=\frac{Pa^{2}}{2\ell^{3}}(a-3\ell ) \;\;\;\; (a<z<\ell )$
曲げモーメントは、
$M_{左}=-EIv_{左}''=-Az-B$
$=\frac{P}{2\ell^{3}}\{(a^{3}-3\ell a^{2}+2\ell^{3})z -(a^{3}-3\ell a^{2}+2\ell^{2}a)\ell \} \;\;\;\; (0<z<a)$
$M_{右}=-EIv_{右}''=-Fz-G$
$=\frac{Pa^{2}}{2\ell^{3}}\{(a-3\ell )z-(a-3\ell )\ell \} \;\;\;\; (a<z<\ell )$

./png/kotehina.png

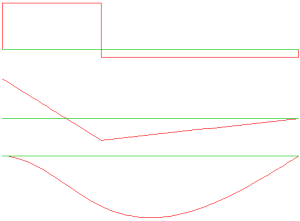
./png/kotehinasmv.png

メモ: