
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 前回、
不静定梁の途中に集中外力や部分的な分布荷重等がなく、
$q(z)$が梁の全域で1つの式($q(z)=0$)で表される場合について、
$-EIv''''(z)+q(z)=0$を4回積分して、両端の境界条件だけを4つ考慮して、
たわみを求めた。
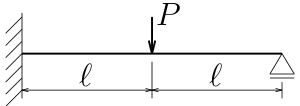
今回は、図のように梁の途中に集中外力がある不静定梁を考える。
$q(z)$自体は、
$0\le z \le \ell$でも
$\ell \le z\le 2\ell$でも
$q(z)=0$で、$z=\ell$のところを考えなければ、
1つの式で表されていると言えなくもないが、
構造力学I第6回の
集中外力を受ける単純梁の曲げモーメントから推測する限り、
恐らく、不静定梁でも、このように梁の途中に集中外力を受けた場合は、
集中外力より左側と右側とで、曲げモーメント$M(z)$は、
異なる式で表されるであろう。
その前提で、
梁を集中外力$P$よりも左側の領域
$0\le z \le \ell$と
右側の領域$\ell \le z\le 2\ell$で場合分けして、
$-EIv''''(z)+q(z)=0$をそれぞれの領域ごとに
積分してみる。
第8回で、
$M(z)=-EIv''(z)$をそれぞれの領域で場合分けしたのと同じ要領だ。
前回、
不静定梁の途中に集中外力や部分的な分布荷重等がなく、
$q(z)$が梁の全域で1つの式($q(z)=0$)で表される場合について、
$-EIv''''(z)+q(z)=0$を4回積分して、両端の境界条件だけを4つ考慮して、
たわみを求めた。
今回は、図のように梁の途中に集中外力がある不静定梁を考える。
$q(z)$自体は、
$0\le z \le \ell$でも
$\ell \le z\le 2\ell$でも
$q(z)=0$で、$z=\ell$のところを考えなければ、
1つの式で表されていると言えなくもないが、
構造力学I第6回の
集中外力を受ける単純梁の曲げモーメントから推測する限り、
恐らく、不静定梁でも、このように梁の途中に集中外力を受けた場合は、
集中外力より左側と右側とで、曲げモーメント$M(z)$は、
異なる式で表されるであろう。
その前提で、
梁を集中外力$P$よりも左側の領域
$0\le z \le \ell$と
右側の領域$\ell \le z\le 2\ell$で場合分けして、
$-EIv''''(z)+q(z)=0$をそれぞれの領域ごとに
積分してみる。
第8回で、
$M(z)=-EIv''(z)$をそれぞれの領域で場合分けしたのと同じ要領だ。
左側の領域($0\le z \le \ell$)のたわみを$v_{左}$,
右側の領域($\ell \le z\le 2\ell$)のたわみを$v_{右}$と書いて
区別することにすると、それぞれの領域で集中外力はなく、
$q(z)=0$だから、
$EIv_{左}''''=0\;\;\;\;(0\le z \le \ell )$
$EIv_{右}''''=0\;\;\;\;(\ell \le z\le 2\ell )$
それぞれ$z$について
4回積分してみると、
$0\le z \le \ell $
について
$EIv''''_{左}=0$
$EIv'''_{左}=A$
$EIv''_{左}=Az+B$
$EIv'_{左}=\frac{A}{2}z^{2}+Bz+C$
$EIv_{左}=\frac{A}{6}z^{3}+\frac{B}{2}z^{2}+Cz+D$
$\ell \le z\le 2\ell $
について
$EIv''''_{右}=0$
$EIv'''_{右}=F$
$EIv''_{右}=Fz+G$
$EIv'_{右}=\frac{F}{2}z^{2}+Gz+H$
$EIv_{右}=\frac{F}{6}z^{3}+\frac{G}{2}z^{2}+Hz+J$
となる。積分定数が$A,B,C,D,F,G,H,J$の8個あるので、
条件式が8個必要である。
まず境界条件として使えるのは、
左の固定端でたわみとたわみ角が0つまり
$v_{左}(0)=0$,
$v'_{左}(0)=0$
と
右のローラー支承でたわみとモーメントが0つまり
$v_{右}(2\ell )=0$,
$v''_{右}(2\ell )=0$
の4つの条件で、これらの条件から、
$C=0$
$D=0$
$G=-2F\ell $
$J=\frac{8}{3}F\ell^{3}-2H\ell $
となる。
これらを代入して式を書き直すと、
$0\le z \le \ell $
について
$EIv''''_{左}=0$
$EIv'''_{左}=A$
$EIv''_{左}=Az+B$
$EIv'_{左}=\frac{A}{2}z^{2}+Bz$
$EIv_{左}=\frac{A}{6}z^{3}+\frac{B}{2}z^{2}$
$\ell \le z\le 2\ell $
について
$EIv''''_{右}=0$
$EIv'''_{右}=F$
$EIv''_{右}=Fz-2F\ell $
$EIv'_{右}=\frac{F}{2}z^{2}-2F\ell z+H$
$EIv_{右}=\frac{F}{6}z^{3}-F\ell z^{2}+Hz+\frac{8}{3}F\ell^{3}-2H\ell $
となる。
第8回でやった
連続条件が使えるのは、
中央の集中荷重載荷部で、たわみとたわみ角が等しい、つまり
$v_{左}(\ell )=v_{右}(\ell )$
$v'_{左}(\ell )=v'_{右}(\ell )$
の2つの条件で、これらの条件から、
$\frac{A}{2}\ell^{2}+B\ell +\frac{3F}{2}\ell^{2}=H$と
$\frac{A}{6}\ell^{2}+\frac{B}{2}\ell -\frac{11}{6}F\ell^{2}=-H$
の2式が求まり、辺々足して整理すると、
$4A\ell +9B-2F\ell =0$
となる。
さて、未知数8個に対して境界条件4つと、連続条件2つ使ったが、
あと2つの条件式が必要である。
ここで、中央の集中荷重載荷部の微小部分を図のように薄くスライスして
切り取ってみる。
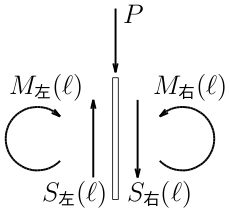 この微小部分の切断面に作用するせん断力と曲げモーメントは、
第9回でやった公式を用いて、
$v_{左}$と$v_{右}$の微分を使って表すことができる。
左の切断面は、$z=\ell$より僅かに左側と考えて$v_{左}$の微分を適用し、
右の切断面は、$z=\ell$より僅かに右側と考えて$v_{右}$の微分を適用すると、
左の切断面にはせん断力$S_{左}(\ell )=-EIv_{左}'''(\ell)$と
曲げモーメント$M_{左}(\ell )=-EIv_{左}''(\ell)$が作用し、
右の切断面にはせん断力$S_{右}(\ell )=-EIv_{右}'''(\ell)$と
曲げモーメント$M_{右}(\ell )=-EIv_{右}''(\ell)$が作用し、
微小部分に集中荷重外力$P$が作用している。
この微小部分の切断面に作用するせん断力と曲げモーメントは、
第9回でやった公式を用いて、
$v_{左}$と$v_{右}$の微分を使って表すことができる。
左の切断面は、$z=\ell$より僅かに左側と考えて$v_{左}$の微分を適用し、
右の切断面は、$z=\ell$より僅かに右側と考えて$v_{右}$の微分を適用すると、
左の切断面にはせん断力$S_{左}(\ell )=-EIv_{左}'''(\ell)$と
曲げモーメント$M_{左}(\ell )=-EIv_{左}''(\ell)$が作用し、
右の切断面にはせん断力$S_{右}(\ell )=-EIv_{右}'''(\ell)$と
曲げモーメント$M_{右}(\ell )=-EIv_{右}''(\ell)$が作用し、
微小部分に集中荷重外力$P$が作用している。
この集中荷重外力が作用する微小部分のつりあい条件を考えると
$\sum\downarrow=-S_{左}(\ell )+P+S_{右}(\ell )=0$
となる。また、このスライスの厚さが0だとしてモーメントの
つりあいを考えると
$\sum\circlearrowleft=-M_{左}(\ell )+M_{右}(\ell )=0$
となる。
これらをたわみの微分を用いて書き直すと、以下のようになる。
$-(-EIv_{左}'''(\ell ))+P+(-EIv_{右}'''(\ell ))=0$
$-(-EIv_{左}''(\ell ))+(-EIv_{右}''(\ell ))=0$
と書け、残りの2つの条件式が得られる。
これらの式から
$A=F-P$
$A\ell +B=-F\ell $
が得られる。
まず、
$4A\ell +9B-2F\ell =0$
$A=F-P$
$A\ell +B=-F\ell $
の$A,B,F$についての連立方程式を解けば、
$B=\frac{3}{8}P\ell $
$F=\frac{5}{16}P$
$A=-\frac{11}{16}P$
が求まる。すると、
$H=\frac{A}{2}\ell^{2}+B\ell +\frac{3F}{2}\ell^{2}=\frac{P\ell^{2}}{2}$と
$G=-2F\ell =-\frac{5}{8}P\ell $
が求まり、
$J=\frac{8}{3}F\ell^{3}-2H\ell =-\frac{P\ell^3}{6}$
が求まる。
よって、
$v_{左}(z)=\frac{P}{96EI}(-11z^{3}+18\ell z^{2})\\$
$v_{右}(z)=\frac{P}{96EI}(5z^{3}-30\ell z^{2}+48\ell^{2}z-16\ell^{3})$
まとめると、
$
v(z)=
\begin{cases}
\frac{P}{96EI}(-11z^{3}+18\ell z^{2})
\;\;\;\;&(0\le z \le \ell )\\
\frac{P}{96EI}(5z^{3}-30\ell z^{2}+48\ell^{2}z-16\ell^{3})
\;\;\;\;&(\ell \le z\le 2\ell)
\end{cases}
$
せん断力は、
$S_{左}(z)=-EIv_{左}'''(z)=-A=\frac{11}{16}P\\$
$S_{右}(z)=-EIv_{右}'''(z)=-F=-\frac{5}{16}P$
まとめると
$
S(z)=
\begin{cases}
\frac{11}{16}P
\;\;\;\;&(0\le z \le \ell )\\
-\frac{5}{16}P
\;\;\;\;&(\ell \le z\le 2\ell )
\end{cases}
$
曲げモーメントは、
$M_{左}(z)=-EIv_{左}''(z)=-Az-B=\frac{P}{16}(11z-6\ell )$
$M_{右}(z)=-EIv_{右}''(z)=-Fz-G=\frac{5P}{16}(-z+2\ell )$
$M_{左}(\ell )=M_{右}(\ell )=\frac{5}{16}P\ell $
まとめると
$M(z)=
\begin{cases}
\frac{P}{16}(11z-6\ell )
\;\;\;\;&(0\le z \le \ell )\\
\frac{5P}{16}(2\ell-z)
\;\;\;\;&(\ell \le z\le 2\ell )
\end{cases}
$
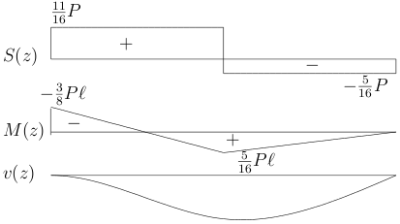 $S$-図、$M$-図、$v$-図。
$S$-図、$M$-図、$v$-図。
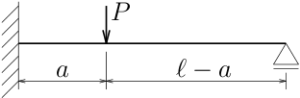
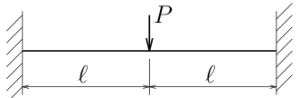 図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
答えはここ。
 図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
答えはここ。
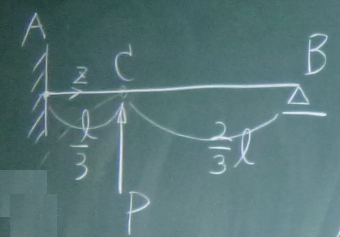 図の不静定梁のたわみ$v(z)$を、
$-EIv''''(z)+q(z)=0$を4回積分して求めたい。
図の不静定梁のたわみ$v(z)$を、
$-EIv''''(z)+q(z)=0$を4回積分して求めたい。
$v(z)=
\begin{cases}
v_{1}(z)\;\;\;\;&(0\le z\le \frac{\ell}{3})\\
v_{2}(z)\;\;\;\;&(\frac{\ell}{3}\le z\le \ell)\\
\end{cases}
$
とおくとき、
①境界条件(4つ)
②点Cでの連続条件(2つ)
③点Cでのつりあい条件(2つ)
を$v$の微分を用いた式で表わせ。
答えはここ。
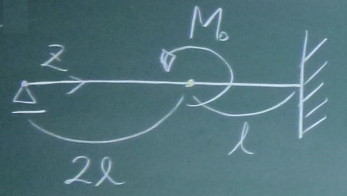 図の不静定梁のたわみ$v(z)$を、
$-EIv''''(z)+q(z)=0$を4回積分して求めたい。
図の不静定梁のたわみ$v(z)$を、
$-EIv''''(z)+q(z)=0$を4回積分して求めたい。
$v(z)=
\begin{cases}
v_{1}(z)\;\;\;\;&(0\le z\le 2\ell)\\
v_{2}(z)\;\;\;\;&(2\ell\le z\le 3\ell)\\
\end{cases}
$
とおくとき、
①境界条件(4つ)
②点Cでの連続条件(2つ)
③点Cでのつりあい条件(2つ)
を$v$の微分を用いた式で表わせ。
答えはここ。
2022年度小テスト:
小テスト230111
2021年度小テスト:
問,
解答
2020年度小テスト:
問1-3
(境界条件4つ、$z=3L$での連続条件2つ、
$z=3L$でのつりあい条件2つ),
解答
メモ: