
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
さて、前回は、 梁の全領域$(0\le z\le \ell)$で曲げモーメント$M(z)$が 1つの式で表されて、場合分けの必要のない場合について、 $M(z)=-EIv''(z)$を積分して、梁のたわみ$v(z)$を求めた。 今回は、梁の途中に集中荷重があって、$M(z)$の式が場合分けされている 場合について、たわみ$v(z)$を求めてみよう。
 という訳で、
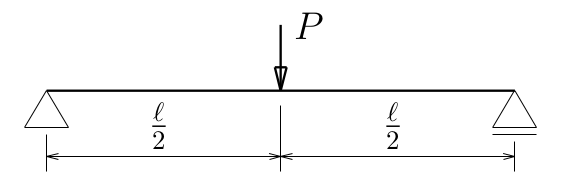
図のような中央に集中荷重を受ける単純支持梁について、
上の2階の微分方程式を使ってたわみを求めてみる。
梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。
この梁の曲げモーメント分布は、
構造力学I第5回の要領で
各自 求めてほしいが、
という訳で、
図のような中央に集中荷重を受ける単純支持梁について、
上の2階の微分方程式を使ってたわみを求めてみる。
梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。
この梁の曲げモーメント分布は、
構造力学I第5回の要領で
各自 求めてほしいが、
$
M(z)=
\begin{cases}
\frac{P}{2}z & \;\;\;\;(0\le z \le \frac{\ell}{2}) \\
\frac{P}{2}(\ell-z) & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)
\end{cases}
\ \\
$
となる。
便宜上、
$0\le z\le\frac{\ell}{2}$の左半分のたわみを$v_{左}$と書いて、
$\frac{\ell}{2}\le z\le \ell$
の右半分のたわみを$v_{右}$と書くことにすると、
$-EIv_{左}=\frac{P}{2}z$
$-EIv_{右}=\frac{P}{2}(\ell-z)$
となるので、それぞれの領域について、
2回積分してみる。
$0\le z\le\frac{\ell}{2}$について
$-EIv''_{左}=\frac{P}{2}z$
$-EIv'_{左}=\frac{P}{4}z^{2}+A$
$-EIv_{左}=\frac{P}{12}z^{3}+Az+B$
$\frac{\ell}{2}\le z\le \ell$について
$-EIv''_{右}=\frac{P}{2}(\ell-z)$
$-EIv'_{右}=\frac{P}{2}(\ell z-\frac{z^{2}}{2})+C$
$-EIv_{右}=\frac{P}{2}(\frac{\ell}{2}z^{2}-\frac{z^{3}}{6})+Cz+D$
そうすると、$A, B, C, D$の4つの積分定数が未知数となる。
この4つの未知数を求めるには、4つの条件式が必要になる。
前回、単純梁では
両端でたわみが0という境界条件が使えた。
今回は、領域ごとにたわみの式が違うので、
左端の境界条件は$v_{左}$に、
右端の境界条件は$v_{右}$に与える必要があるので注意する。
その辺の間違いを防止するために、
$v_{左}, v_{右}$とか、$v_{L}, v_{R}$とか、領域ごとのたわみの
式を区別しておいた方が安全だろう。
境界条件:
$v_{左}(0)=0$
$v_{右}(\ell)=0$
積分定数は4つなので、あと2つ条件式がないと、
積分定数を決定できない。
梁の途中に集中荷重があったりして、領域の場合分けのある問題の場合は、
領域の境界点(今回は$z=\frac{\ell}{2}$)での連続条件を用いる。
 連続条件というのは、梁の変位やたわみ角は領域の境界でも連続しているという条件で、
図のように梁が領域の境界点でちぎれたり(変位が不連続)、
折れ曲がったり(たわみ角が不連続)ということは起きないという条件である。
連続条件というのは、梁の変位やたわみ角は領域の境界でも連続しているという条件で、
図のように梁が領域の境界点でちぎれたり(変位が不連続)、
折れ曲がったり(たわみ角が不連続)ということは起きないという条件である。
$v_{左}(\frac{\ell}{2})=v_{右}(\frac{\ell}{2})\;\;\;\;$ 中央でちぎれない
$v'_{左}(\frac{\ell}{2})=v'_{右}(\frac{\ell}{2})\;\;\;\;$ 中央で折れ曲がらない
以上で、条件式が4つになったので、
積分定数$A, B, C, D$を求めることができそうだ。
という訳で、これらの条件式を書き出してみると、
$v_{左}(0)=0$ から $B=0$
$v_{右}(\ell)=0$ から $\ell C+D=-\frac{P\ell^{3}}{6}$
$v_{左}(\frac{\ell}{2})=v_{右}(\frac{\ell}{2})$
から $\frac{\ell}{2}A-\frac{\ell}{2}C-D=\frac{P\ell^{3}}{24}$
$v'_{左}(\frac{\ell}{2})=v'_{右}(\frac{\ell}{2})$
から $A-C=\frac{P\ell^{2}}{8}$
という $A, B, C, D$ に関する連立方程式になるので、
これを解くと、
$A=-\frac{P\ell^{2}}{16}$
$B=0$
$C=-\frac{3P\ell^{2}}{16}$
$D=\frac{P\ell^{3}}{48}$
と求まる。よって、これらを$v_{左}$と$v_{右}$に代入すると
梁のたわみは、
$v_{左}(z)=\frac{P}{48EI}(3\ell^{2}z-4z^{3})$
$(0\le z\le\frac{\ell}{2})$
$v_{右}(z)=\frac{P}{48EI}(4z^{3}-12\ell z^{2}+9\ell^{2}z-\ell^{3})$
$(\frac{\ell}{2}\le z\le \ell)$
と求まる。
まとめると、以下のようになる。
$
v(z)=
\begin{cases}
\frac{P}{48EI}(3\ell^{2}z-4z^{3})\;\;\;\;
(0\le z\le\frac{\ell}{2})\\
\frac{P}{48EI}(4z^{3}-12\ell z^{2}+9\ell^{2}z-\ell^{3})\;\;\;\;
(\frac{\ell}{2}\le z\le \ell)
\end{cases}
$
ちなみに、この問題は左右対称なので、載荷点の梁中央における
たわみ角がたまたま0であるという条件を利用するなら、
$v'_{左}(\frac{\ell}{2})=0$から
$A=-\frac{P\ell^{2}}{16}$を、
$v'_{右}(\frac{\ell}{2})=0$から
$C=-\frac{3P\ell^{2}}{16}$を求めることもできる。
なお、載荷点の中央部のたわみは、
$v_{左}(\frac{\ell}{2})=v_{右}(\frac{\ell}{2})=\frac{P\ell^{3}}{48EI}$となる。
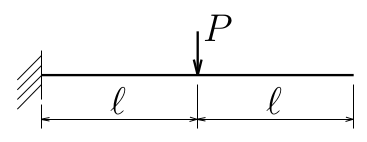 図のように
梁の中央に集中荷重を受ける片持ち梁のたわみを求めてみよう。
曲げ剛性は$EI$とする。
曲げモーメントは各自 求めてみよう。
載荷点より固定端側は、構造力学I第6回の例題と
同じ。載荷点より自由端側は、
これとかが参考になるか。
曲げモーメントは以下のように求まる。
図のように
梁の中央に集中荷重を受ける片持ち梁のたわみを求めてみよう。
曲げ剛性は$EI$とする。
曲げモーメントは各自 求めてみよう。
載荷点より固定端側は、構造力学I第6回の例題と
同じ。載荷点より自由端側は、
これとかが参考になるか。
曲げモーメントは以下のように求まる。
$
M=
\begin{cases}
-P(\ell-z)\;\;\;\;&(0\le z\le\ell)\\
0\;\;\;\;\;\;\;\;&(\ell \le z \le 2\ell)
\end{cases}
$
$0\le z\le\ell$について
$M=-P(\ell-z)$
$M=-EIv''$より
$EIv_{左}''=P(\ell-z)$
$EIv_{左}'=P(\ell z-\frac{z^{2}}{2})+A$
$EIv_{左}=P(\frac{\ell}{2}z^{2}-\frac{z^{3}}{6})+Az+B$
境界条件:$v_{左}(0)=0, v_{左}'(0)=0$ より $B=0, A=0$
境界条件や連続条件を与える場合、右端だからといって$v(\ell)$とは限らないし、
真ん中だからといって$v(\frac{\ell}{2})$とは限らない。
ちゃんと条件を与える点の$z$座標を確認すること。
$v_{左}(z)=\frac{P}{6EI}(3\ell z^{2}-z^{3})$
$\ell \le z \le 2\ell$について
$M=0$
$M=-EIv''$より、
$EIv_{右}''=0$
$EIv_{右}'=C$
$EIv_{右}=Cz+D$
連続条件: $v'_{左}(\ell)=v'_{右}(\ell)$,
$v_{左}(\ell)=v_{右}(\ell)$より
$C=\frac{P\ell^{2}}{2}$, $D=-\frac{P\ell^{3}}{6}$
$v_{右}=\frac{P}{6EI}(3\ell^{2}z-\ell^{3})$
以上をまとめると
$
v(z)=
\begin{cases}
\frac{P}{6EI}(3\ell z^{2}-z^{3}) \;\;\;\; &(0\le z\le \ell)\\
\frac{P}{6EI}(3\ell^{2}z-\ell^{3}) \;\;\;\; &(\ell\le z\le 2\ell)\\
\end{cases}
$
先端のたわみ: $v_{右}(2\ell)=\frac{5P\ell^{3}}{6EI}$

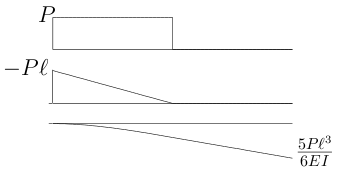
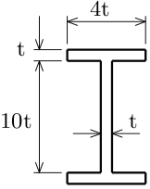 また、この梁が図のような2軸対称の$\text{I}$型断面をしている場合、
前回やったように
直応力の最大値と、それが発生する場所$(y,z)$を求めてみよう。
また、この梁が図のような2軸対称の$\text{I}$型断面をしている場合、
前回やったように
直応力の最大値と、それが発生する場所$(y,z)$を求めてみよう。
図心軸(中立軸)回りの
断面2次モーメントは、$4t\times 12t$の大きい長方形から、
$1.5t\times 10t$の小さい長方形2個ぶん
(つまり$3t\times 10t$の小さい長方形1個ぶん)を引けばいい。
$I=\frac{4t(12t)^{3}}{12}-\frac{3t(10t)^{3}}{12}$
$=326t^{4}$
$M$-図より$M_{max}=M(0)=-P\ell$
$\sigma_{zz}=\frac{M}{I}y$より
$\sigma_{zz}(y=-6t, z=0)=\frac{-P\ell}{326t^{4}}(-6t)=\frac{3P\ell}{163t^{3}}$
$\sigma_{zz}(y=6t, z=0)=\frac{-P\ell}{326t^{4}}(6t)=-\frac{3P\ell}{163t^{3}}$
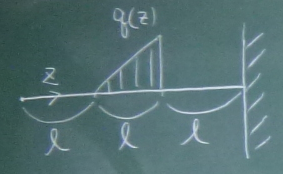 図のように、一箇所に三角形分布荷重を受ける片持ち梁の
たわみを求めたい。
曲げモーメント$M(z)$は、荷重のない領域と荷重のある領域で
場合分けする必要があるので、それに応じて、たわみ$v(z)$も
以下のように場合分けする。
図のように、一箇所に三角形分布荷重を受ける片持ち梁の
たわみを求めたい。
曲げモーメント$M(z)$は、荷重のない領域と荷重のある領域で
場合分けする必要があるので、それに応じて、たわみ$v(z)$も
以下のように場合分けする。
$v(z)=
\begin{cases}
v_{1}(z)\;\;\;\;&(0\le z \le \ell)\\
v_{2}(z)\;\;\;\;&(\ell\le z \le 2\ell)\\
v_{3}(z)\;\;\;\;&(2\ell\le z \le 3\ell)
\end{cases}
$
$M(z)=-EIv''(z)$を積分してたわみ$v(z)$を求めたいが、
各領域ごとに2つずつの積分定数ができるから、
3つの領域で計6個の積分定数ができる。
これらの積分定数を決定するのに
必要な境界条件、連続条件を
$v_{1}, v_{2}, v_{3}$を用いて列挙せよ。
答えはここ。
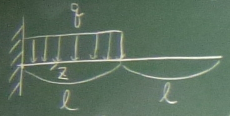 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
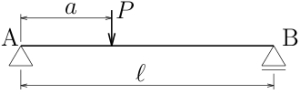 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
答えはここ。
2022年度小テスト:
小テスト221207
2021年度小テスト:
問,
解答
2020年度小テスト:
問1,
問2,
解答
メモ: