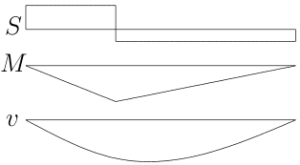
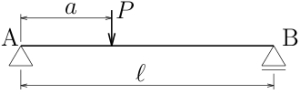
 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
 図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
図の片持ち梁のたわみ$v(z)$を求めよ。曲げ剛性は$EI$とする。
鉛直方向の力のつりあい: $-V_{A}+P-V_{B}=0$
A点左回りのモーメントのつりあい: $-aP+\ell V_{B}=0$
$V_{B}=\frac{a}{\ell }P$
$V_{A}=\frac{\ell -a}{\ell }P$
便宜上、$0\le z\le a$の領域の断面力やたわみに添字$\ _{左}$を、
$a\le z\le \ell $の領域の断面力やたわみに添字$\ _{右}$を
つけて表すことにすると、
$0\le z\le a$について、断面を切ってつりあいを考えると
$S_{左}=\frac{\ell -a}{\ell }P$
$M_{左}=\frac{\ell -a}{\ell }Pz$
$a\le z\le \ell $について、断面を切ってつりあいを考えると
$S_{右}=-\frac{a}{\ell }P$
$M_{右}=\frac{a}{\ell }P(\ell -z)$
$M=-EIv''$より
$0\le z\le a$について
$EIv_{左}''=\frac{a-\ell }{\ell }Pz$
$EIv_{左}'=\frac{a-\ell }{2\ell }Pz^{2}+A$
$EIv_{左}=\frac{a-\ell }{6\ell }Pz^{3}+Az+B$
$a\le z\le \ell $について
$EIv_{右}''=\frac{a}{\ell }P(z-\ell )$
$EIv_{右}'=\frac{a}{\ell }P(\frac{z^{2}}{2}-\ell z)+C$
$EIv_{右}=\frac{a}{\ell }P(\frac{z^{3}}{6}-\frac{\ell }{2}z^{2})+Cz+D$
境界条件は両端でたわみが$0$, つまり
$v_{左}(0)=0, v_{右}(\ell )=0$
これらより
$B=0$
$D=\frac{a\ell^{2}P}{3}-C\ell $
$EIv_{右}=\frac{a}{\ell }P(\frac{z^{3}}{6}-\frac{\ell }{2}z^{2})+Cz+\frac{a\ell^{2}P}{3}-C\ell $
連続条件は、$z=a$でたわみとたわみ角がそれぞれ連続、つまり
$v_{左}(a)=v_{右}(a)$
$v_{左}'(a)=v_{右}'(a)$
これらより
$C=\frac{Pa}{6\ell }(2\ell^{2}+a^{2})$
$A=\frac{Pa}{6\ell }(a-\ell )(a-2\ell )$
よって、たわみは、
$v_{左}=\frac{P(a-\ell )}{6\ell EI}\{z^{3}+(a^{2}-2\ell a)z\}
\;\;\;\;
(0\le z\le a)$
$v_{右}=\frac{Pa}{6\ell EI}\{(z^{3}-3\ell z^{2})+(2\ell^{2}+a^{2})z-a^{2}\ell \}
\;\;\;\;
(a\le z\le \ell )$
以上をまとめると、
$v(z)=
\begin{cases}
\frac{P(a-\ell )}{6\ell EI}\{z^{3}+(a^{2}-2\ell a)z\}
\;\;\;\;&
(0\le z\le a)\\
\frac{Pa}{6\ell EI}\{(z^{3}-3\ell z^{2})+(2\ell^{2}+a^{2})z-a^{2}\ell \}
\;\;\;\;&
(a\le z\le \ell )\\
\end{cases}
$