
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
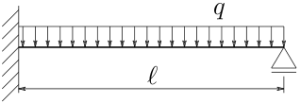 前回 導いた梁の支配微分方程式
前回 導いた梁の支配微分方程式
$-EIv''''(z)+q(z)=0$
を用いて、図のような1次不静定の梁を解いてみよう。
左端から右端まで等分布荷重が作用する問題は、
場合分けしなくていいから、
4回積分すると積分定数が4つですみ、
両端の境界条件だけで解けてしまう。
梁の支配微分方程式は$-EIv''''+q=0$だから、
$EIv''''=q\;\;\;\;$これを4回積分していく。
$EIv'''=qz+A$
$EIv''=\frac{q}{2}z^{2}+Az+B$
$EIv'=\frac{q}{6}z^{3}+\frac{A}{2}z^{2}+Bz+C$
$EIv=\frac{q}{24}z^{4}+\frac{A}{6}z^{3}+\frac{B}{2}z^{2}+Cz+D$
4回積分すると、$A, B, C, D$の4つの積分定数ができる。
境界条件は、左端でたわみとたわみ角が$0$から、
$v(0)=0, v'(0)=0$
これは、まあいいだろう。あと、右端がローラー支承でたわみはないから、
$v(\ell )=0$
これもまあいいだろう。
積分定数は4つだから、あと1つ境界条件が必要だ。
右端はローラー支承で、回転を許すから、モーメント反力は発生しない。
曲げモーメントは$M(z)=-EIv''(z)$で表されるから、
$M(\ell)=-EIv''(\ell)=0$が使える。つまり、
$v''(\ell )=0$
これで条件式が4つになり、積分定数が求まる。
$EIv'(0)=C=0$
$EIv(0)=D=0$
$EIv''(\ell)=\frac{q}{2}\ell^{2}+A\ell+B=0$
$EIv(\ell)=\frac{q}{24}\ell^{4}+\frac{A}{6}\ell^{3}+\frac{B}{2}\ell^{2}=0$
これらを連立させて
$A=-\frac{5}{8}q\ell $
$B=\frac{q\ell^{2}}{8}$
よってたわみは
$v=\frac{q}{48EI}(2z^{4}-5\ell z^{3}+3\ell^{2}z^{2})$
せん断力は
$S=-EIv'''=-qz-A=\frac{q}{8}(-8z+5\ell )$
曲げモーメントは
$M=-EIv''=-\frac{q}{2}z^{2}-Az-B=\frac{q}{8}(-4z^{2}+5\ell z-\ell^{2})$
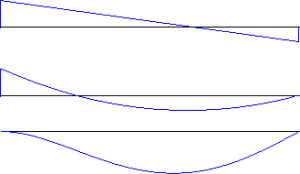 $S(z)$や$M(z)$を求めれば、せん断力図や曲げモーメント図も描ける。
図は、$S$-図、$M$-図、$v$-図。
反力は、
前回の例題参照。
$S(z)$や$M(z)$を求めれば、せん断力図や曲げモーメント図も描ける。
図は、$S$-図、$M$-図、$v$-図。
反力は、
前回の例題参照。
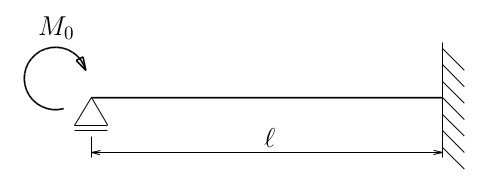 今度は、図のように不静定梁が端部に外力モーメントを受ける問題を解いてみよう。
この問題は、端部に外力モーメント$M_{0}$が作用しているものの、
梁の途中に外力はなく、$q(z)=0$となり
$q(z)$は$0\le z\le\ell$で1つの式で表されるので場合分けは不要である。
$-EIv''''(z)+q(z)=0$から、
今度は、図のように不静定梁が端部に外力モーメントを受ける問題を解いてみよう。
この問題は、端部に外力モーメント$M_{0}$が作用しているものの、
梁の途中に外力はなく、$q(z)=0$となり
$q(z)$は$0\le z\le\ell$で1つの式で表されるので場合分けは不要である。
$-EIv''''(z)+q(z)=0$から、
$-EIv''''=0$ となるが、右辺が0なので、$-EI$で割ってしまおう。
$v''''=0\;\;\;\;$ もちろん、$-EI$をつけたまま計算したい人はそれでもよい。
積分定数が変わってくるだけの話だ。
これを4回積分していく。
ついでに、分数の計算がいやな人は、4回積分したものを
$v=az^{3}+bz^{2}+cz+d$みたいにおいてしまうというやり方もある。
$v'''=A$
$v''=Az+B$
$v'=\frac{A}{2}z^{2}+Bz+C$
$v=\frac{A}{6}z^{3}+\frac{B}{2}z^{2}+Cz+D$
境界条件は、右端が固定端でたわみとたわみ角がないので、
$v(\ell)=0, v'(\ell)=0$
左端はローラー支承でたわみがないので、
$v(0)=0$
ここまではいいだろう。
さて、ローラー支承は、
上の問題では、
ヒンジが回転を許すからモーメントは発生しないと言ったが、
今回は、ローラー支承にモーメント外力が作用している。
つまり、ローラー支承部の曲げモーメント$M(0)=-EIv''(0)$は0にはならずに、
モーメント外力とつりあうことになる。
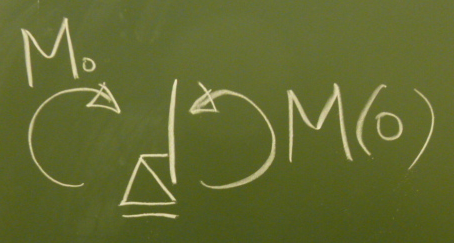 ローラー支承部の近傍($z=0$に限りなく近いところ)を切断して、
モーメントのつりあいを考えてやる。
ローラー支承部の近傍($z=0$に限りなく近いところ)を切断して、
モーメントのつりあいを考えてやる。
$\sum\circlearrowleft=-M_{0}+M(0)=0\;\;\;\;$つまり
$M(0)=-EIv''(0)=M_{0}\;\;\;\;$が条件式として使える。つまり
$-EIv''(0)=-EI(A\cdot 0+B)=M_{0}$から $B=-\frac{M_{0}}{EI}$
$v(0)=D=0$
$v'(\ell)=\frac{A}{2}\ell^{2}-\frac{M_{0}}{EI}\ell+C=0$
$v(\ell)=\frac{A}{6}\ell^{3}-\frac{M_{0}}{2EI}\ell^{2}+C\ell=0$
これらを連立させて
$C=\frac{M_{0}\ell}{4EI}\\$
$A=\frac{3M_{0}}{2\ell EI}$
よってたわみは、
$v(z)=\frac{M_{0}}{4\ell EI}(z^{3}-2\ell z^{2}+\ell^{2}z)$
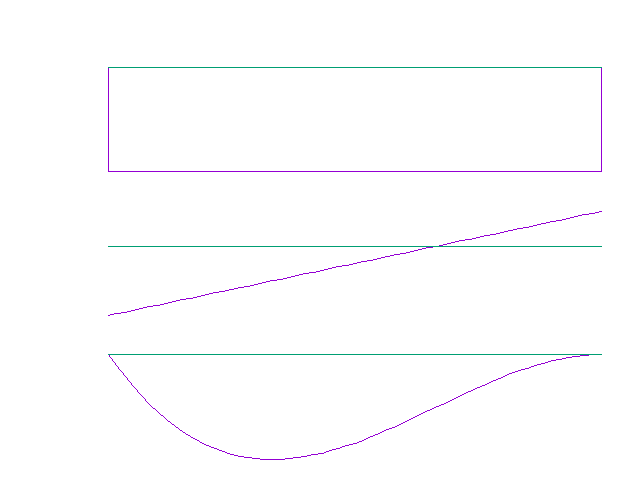 参考までに、$S$-図、$M$-図、$v$-図。
参考までに、$S$-図、$M$-図、$v$-図。
$M(z)=-\frac{M_{0}}{2\ell}(3z-2\ell)$
$S(z)=-\frac{3M_{0}}{2\ell}$
$V_{A}(上が正)=-\frac{3M_{0}}{2\ell}$
$V_{B}(上が正)=\frac{3M_{0}}{2\ell}$
$M_{B}(下側引張が正)=-\frac{M_{0}}{2}$
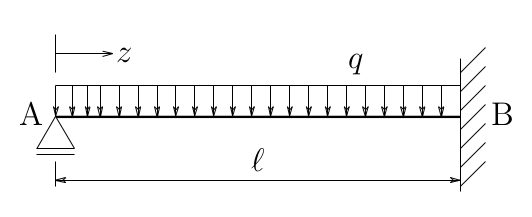 図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
答えはここ。
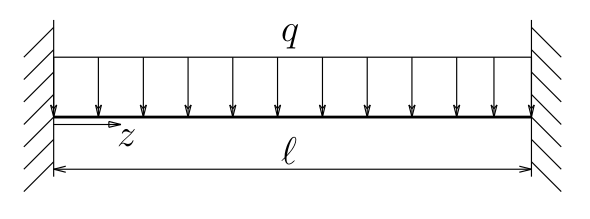 図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
図の不静定梁のたわみを求めよ。
曲げ剛性は$EI$とする。
答えはここ。
2022年度小テスト:
小テスト221221
2021年度小テスト:
問,
解答
2020年度小テスト:
問1-2,
解答
メモ: