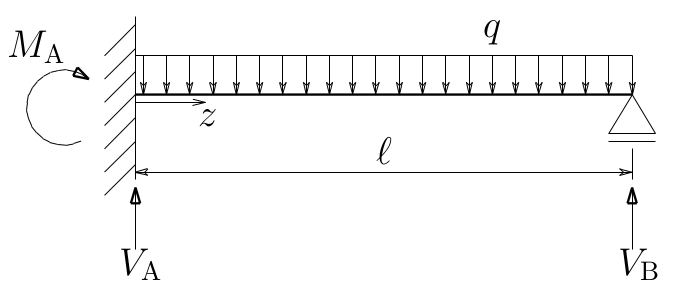
図の不静定梁のたわみが$v(z)=\frac{q}{48EI}(2z^{4}-5\ell z^{3}+3\ell^{2}z^{2})$
で与えられるとき、 せん断力$S(z)$, 曲げモーメント$M(z)$, 反力$V_\text{A}, M_\text{A}, V_\text{B}$を求めよ。
図の不静定梁のたわみが
$v(z)=\frac{q}{48EI}(2z^{4}-5\ell z^{3}+3\ell^{2}z^{2})$
で与えられるとき、
せん断力$S(z)$, 曲げモーメント$M(z)$,
反力$V_\text{A}, M_\text{A}, V_\text{B}$を求めよ。
ここの公式各種を利用するために、
まずは、たわみの3階微分まで求めておく。
$
\begin{array}{rl}
v'(z)=&\frac{q}{48EI}(8z^{3}-15\ell z^{2}+6\ell^{2}z)\\
v''(z)=&\frac{q}{48EI}(24z^{2}-30\ell z+6\ell^{2})\\
=&\frac{q}{8EI}(4z^{2}-5\ell z+\ell^{2})\\
v'''(z)=&\frac{q}{8EI}(8z-5\ell)\\
\end{array}
$
よって、
$S(z)=-EIv'''(z)=-\frac{q}{8}(8z-5\ell)$
$M(z)=-EIv''(z)=-\frac{q}{8}(4z^{2}-5\ell z+\ell^{2})$
$V_\text{A}=S(0)=\frac{5q\ell}{8}$
$V_\text{B}=-S(\ell)=\frac{3q\ell}{8}$
$M_\text{A}=M(0)=-\frac{q\ell^{2}}{8}$
$z=0$や$z=\ell$での$S$や$M$の値と、 反力の符号との関係は、 ここにあるように、 $z=0$や$z=\ell$の近くで梁を切断して、 切断面に$S$や$M$を描き入れ、 力のつりあいを考えればよい。
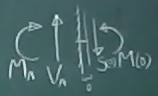$z=0$の近くで長さほぼ0のスライスを切り取る。
$\sum\downarrow=-V_\text{A}+S(0)=0$
$\sum\circlearrowleft=-M_\text{A}+M(0)=0$
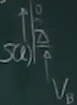$z=\ell$の近くで長さほぼ0のスライスを切り取る。
$\sum\downarrow=-S(\ell)-V_\text{B}=0$
