
構造力学IIオンライン授業用テキスト
第3回オンライン授業
まだ、書き換え途中なので、色々とおかしい記述があります。 小さい字は補足説明や余談なので、読み飛ばしてもいいです。
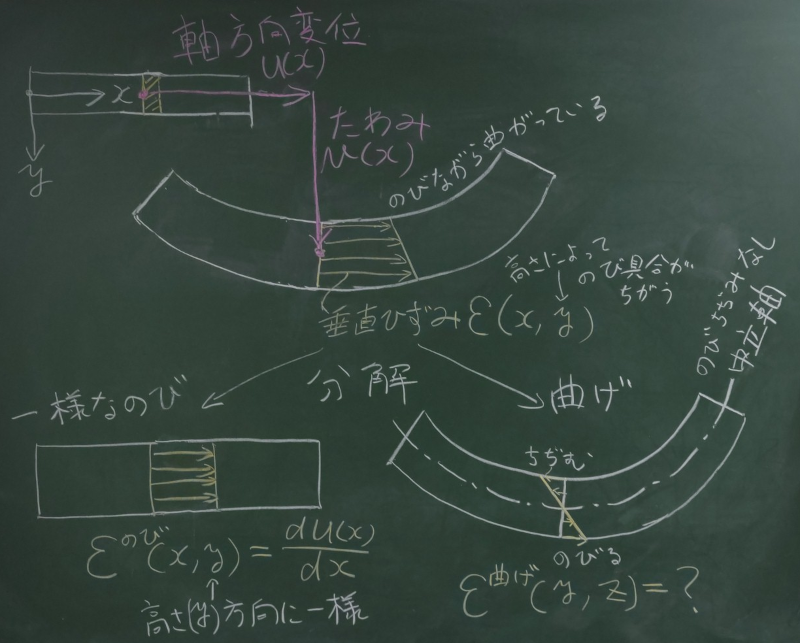 前回の話によると、
初等梁では軸方向の垂直ひずみ$\varepsilon$しか生じないのだが、
断面の各部分が軸方向にしか伸び縮みしないのに、
そんなんで、梁全体はどうやって曲がるんだろうか。
右の絵のように、梁の上の方はちょっとしか伸びなくて(あるいは縮んで)、
梁の下の方がいっぱい伸びると、梁は曲がるのだ。
実際の細長い棒でも、そういうことが起きていると考えられる。
例えば、ひまわりの花が、太陽の方を向く理由を理科で
習うと思うが、茎の光の当たる側はあまり伸びずに、
光の当たらない側の方がよく伸びるから、
茎全体としては、光の方に曲がるということだったと思う。
前回の話によると、
初等梁では軸方向の垂直ひずみ$\varepsilon$しか生じないのだが、
断面の各部分が軸方向にしか伸び縮みしないのに、
そんなんで、梁全体はどうやって曲がるんだろうか。
右の絵のように、梁の上の方はちょっとしか伸びなくて(あるいは縮んで)、
梁の下の方がいっぱい伸びると、梁は曲がるのだ。
実際の細長い棒でも、そういうことが起きていると考えられる。
例えば、ひまわりの花が、太陽の方を向く理由を理科で
習うと思うが、茎の光の当たる側はあまり伸びずに、
光の当たらない側の方がよく伸びるから、
茎全体としては、光の方に曲がるということだったと思う。
そうすると、垂直ひずみ$\varepsilon$は、断面の上の方と下の方とで、 大きさが違うから$\varepsilon(x,y)$みたいに、 軸方向の座標$x$だけではなく、 高さ$y$にも依存する 関数として与えなければならない。 垂直ひずみ$\varepsilon(x,y)$を図心変位$u(x), v(x)$を使って表したいが、 そんなことができるだろうか。
というわけで、まずは、垂直ひずみ$\varepsilon(x,y)$を
右上の絵のような一様な伸び成分
$\varepsilon^{のび}(x,y)$
と一様な曲げ成分
$\varepsilon^{曲げ}(x,y)$
との足し算で表せるように分解してやる。
実際の垂直ひずみ$\varepsilon(x,y)$の分布は、
上の方がちょっとだけ伸びて、下の方がいっぱい伸びてという
台形分布をしているのだけど、
これを「上から下まで一様な伸びの成分」$\varepsilon^{のび}(x,y)$
と
「図心位置ではのびちぢみがなく上がちぢんで下がのびてる成分」
$\varepsilon^{曲げ}(x,y)$
との
足し算に分解するのだ。
$\varepsilon(x,y)=\varepsilon^{のび}(x,y)+\varepsilon^{曲げ}(x,y)$
そうすると、
まず直ひずみの伸び成分
$\varepsilon^{のび}(x,y)$については、
高さ$y$によらずに断面のどの高さでも値は同じなのだから、
これは
図心位置の軸方向変位$u(x)$を用いた
図心位置の垂直ひずみ$\varepsilon(x)=u'(x)$を使って、
$\varepsilon^{のび}(x,y)=u'(x)$と表せるだろう。
高さ方向に一様だから、$y$には依存しない。
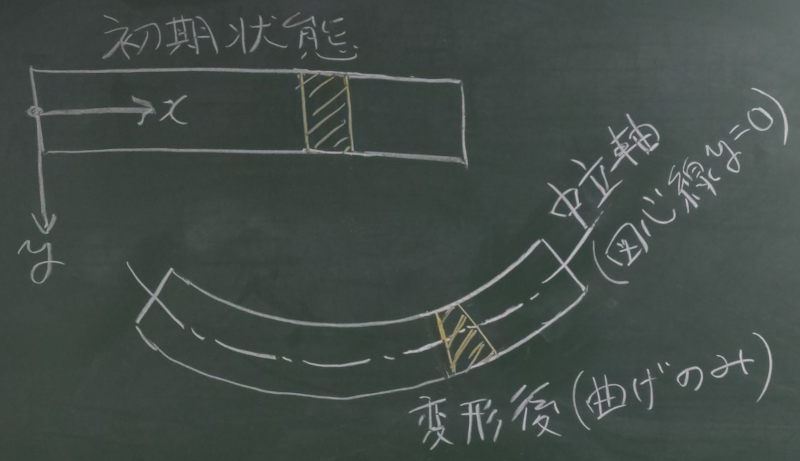 では、垂直ひずみの曲げ成分
$\varepsilon^{曲げ}(x,y)$については、
断面の図心変位の$u(x)$や$v(x)$を使って表せるだろうか。
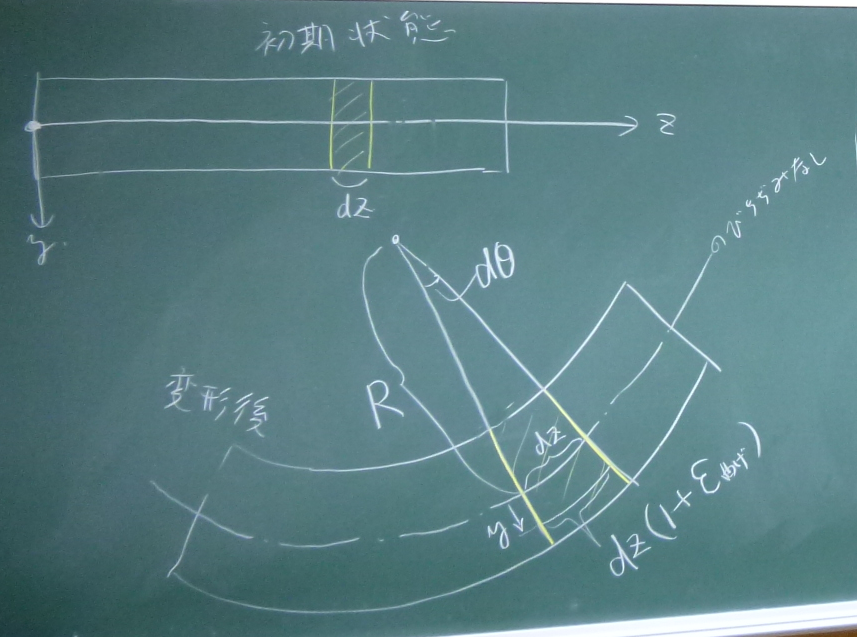
右の絵のように、
初期状態の梁の微小なスライスを考える。
この微小なスライスが梁の変形後、
断面の図心位置($y=0$)は伸び縮みせず、
上の方は縮んで、
下の方は伸びてバームクーヘン状になったものとする。
では、垂直ひずみの曲げ成分
$\varepsilon^{曲げ}(x,y)$については、
断面の図心変位の$u(x)$や$v(x)$を使って表せるだろうか。
右の絵のように、
初期状態の梁の微小なスライスを考える。
この微小なスライスが梁の変形後、
断面の図心位置($y=0$)は伸び縮みせず、
上の方は縮んで、
下の方は伸びてバームクーヘン状になったものとする。
このバームクーヘンを拡大したものを描き直す。
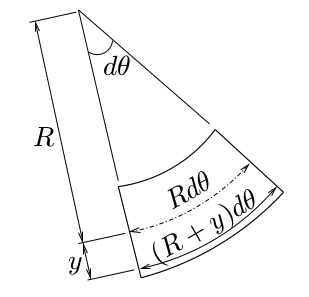 ベルヌーイ・オイラーの仮定により、
断面は上面や図心線や下面と直交しているとする。
このバームクーヘンの(断面の図心を連ねた)図心線の曲率半径を$R$とし、
その中心角を$d\theta$とする。
バームクーヘンの断面の
図心位置($y=0$)は,変形前から伸び縮みしておらず
$Rd\theta$の長さなのに対して,
図心位置から下に$y$下がった位置では,
伸びて$(R+y)d\theta$の長さになっている。
つまり,高さ方向の位置$y$での垂直ひずみは,
変形前の微小部分の長さ(図心位置の長さ)に対する変形後の伸びの比率だから、
垂直ひずみのときの要領で考えると、
次式で表される。
$$\varepsilon^{曲げ}(x,y)=\frac{(R+y)d\theta-Rd\theta}{Rd\theta}=\frac{y}{R}$$
ベルヌーイ・オイラーの仮定により、
断面は上面や図心線や下面と直交しているとする。
このバームクーヘンの(断面の図心を連ねた)図心線の曲率半径を$R$とし、
その中心角を$d\theta$とする。
バームクーヘンの断面の
図心位置($y=0$)は,変形前から伸び縮みしておらず
$Rd\theta$の長さなのに対して,
図心位置から下に$y$下がった位置では,
伸びて$(R+y)d\theta$の長さになっている。
つまり,高さ方向の位置$y$での垂直ひずみは,
変形前の微小部分の長さ(図心位置の長さ)に対する変形後の伸びの比率だから、
垂直ひずみのときの要領で考えると、
次式で表される。
$$\varepsilon^{曲げ}(x,y)=\frac{(R+y)d\theta-Rd\theta}{Rd\theta}=\frac{y}{R}$$
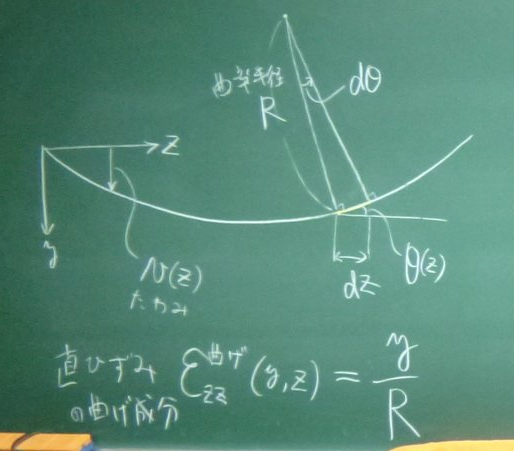
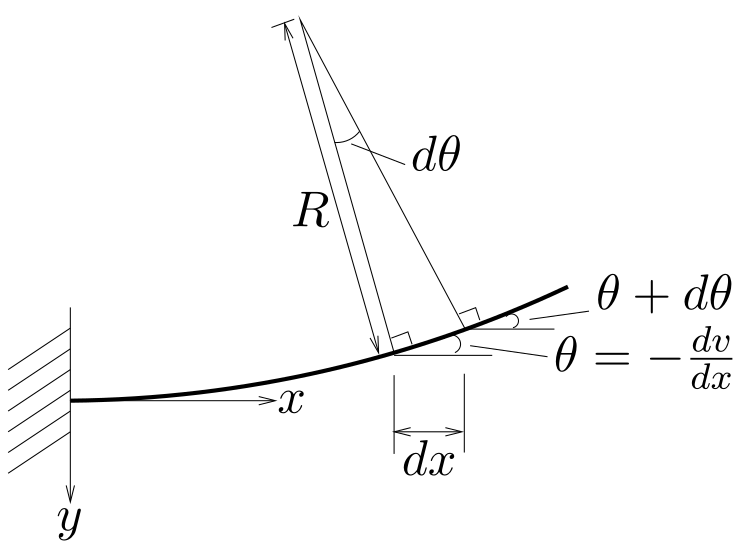 さて,曲率半径$R$と微小な角度$d\theta$, そして
この微小な部分の$x$方向の微小長さ$dx$には,
右の図のように,
近似的に$dx=Rd\theta$のような関係があるから,
${\displaystyle \frac{1}{R}=\frac{d\theta}{dx}}$と変形できる。
$\frac{d\theta}{dx}$は、$d\theta$割る$dx$ということだが、
微小量どうしの割り算は、微分とみなせるので、
$\theta$を$x$で微分したものとみなしてやる。
また,
梁のたわみ$v(x)$が,
$x$の正方向の増加に対して,$y$の負方向に増加する傾きを
${\displaystyle \theta=-\frac{dv}{dx}}$で表すと,
$d\theta$は,$x$から$dx$離れたところで梁がどれだけその傾きを増加させたかを
表している。
まあ、物理的なイメージがわかれば、符号は、そんなに悩まなくてもいい。
さて,曲率半径$R$と微小な角度$d\theta$, そして
この微小な部分の$x$方向の微小長さ$dx$には,
右の図のように,
近似的に$dx=Rd\theta$のような関係があるから,
${\displaystyle \frac{1}{R}=\frac{d\theta}{dx}}$と変形できる。
$\frac{d\theta}{dx}$は、$d\theta$割る$dx$ということだが、
微小量どうしの割り算は、微分とみなせるので、
$\theta$を$x$で微分したものとみなしてやる。
また,
梁のたわみ$v(x)$が,
$x$の正方向の増加に対して,$y$の負方向に増加する傾きを
${\displaystyle \theta=-\frac{dv}{dx}}$で表すと,
$d\theta$は,$x$から$dx$離れたところで梁がどれだけその傾きを増加させたかを
表している。
まあ、物理的なイメージがわかれば、符号は、そんなに悩まなくてもいい。
${\displaystyle \frac{1}{R}=\frac{d\theta}{dx}}$に
${\displaystyle \theta=-\frac{dv}{dx}}$を代入すると、
${\displaystyle \frac{1}{R}=-\frac{d^{2}v(x)}{dx^{2}}}$となる。
これを
${\displaystyle \varepsilon^{曲げ}(x,y)=\frac{y}{R}}$に代入すれば
直ひずみの曲げ成分は
次式のように表される。
$$\varepsilon^{曲げ}(x,y)=-y\frac{d^{2}v(x)}{dx^{2}}=-y\,v''(x)$$
${\displaystyle \frac{1}{R}=-v''(x)}$は, 曲率を表しており,ひずみ$\varepsilon^{曲げ}(x,y)$は,ある$z$点の断面では高さ$y$方向に対して, 曲率に比例する線形分布をしていることがわかる。
さて、 初等梁に発生する唯一の直ひずみ$\varepsilon(x,y)$を 一様な伸び成分と曲げ成分とに分解して、 それぞれを図心変位$u(x)$や$v(x)$の微分を用いて表すことができた。 これらを足し算すると、以下のように表せる。
$\varepsilon(x,y)=\varepsilon^{のび}(x,y)+\varepsilon^{曲げ}(x,y)$
つまり、
$\varepsilon(x,y)=u'(x)-y\,v''(x)$
この(梁限定の)直ひずみの 伸び成分$\varepsilon^{のび}(x,y)=u'(x)$のことを「のびひずみ」や「軸ひずみ」と 言ったり、 曲げ成分 $\varepsilon^{曲げ}(x,y)=-y\,v''(x)$ のことを「曲げひずみ」と言ったりする習慣(特に後者)もあるかもしれない。 しかし、 これらは、あくまで梁の垂直ひずみの のび成分と曲げ成分であって、 一般的な物体の 垂直ひずみと せん断ひずみという区別の他に 「のびひずみ」や 「曲げひずみ」があるわけではないので混乱しないように。 だから、ここでは、いちいち「垂直ひずみののび成分」とか「垂直ひずみの曲げ成分」と 言うようにしている。
 さて、梁モデルで考慮しなければならないひずみは、梁の軸($x$)方向の
垂直ひずみで、次式のように表されることがわかった。
さて、梁モデルで考慮しなければならないひずみは、梁の軸($x$)方向の
垂直ひずみで、次式のように表されることがわかった。
$\varepsilon(x,y)=u'(x)-y\,v''(x)$
今、梁のある断面、例えば$x=x_{A}$でのひずみの分布がどうなっているかを
考えてみる。上の式に、
$x=x_{A}$を代入してみると、
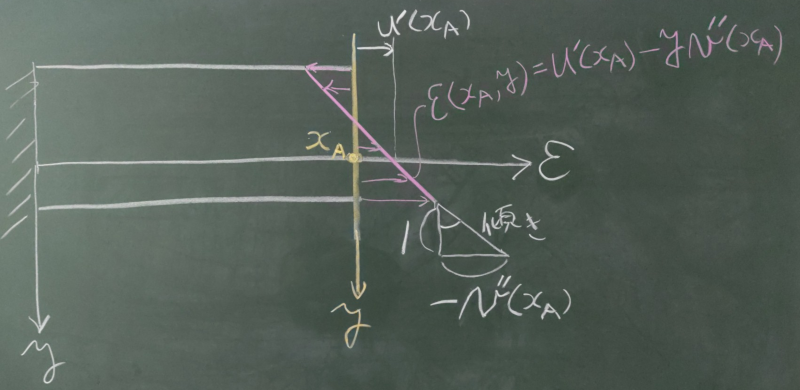
$\varepsilon(x_{A},y)=u'(x_{A})-yv''(x_{A})$
となる。$x_{A}$はある座標の値で、定数だから
$u'(x_{A})$や$v''(x_{A})$も定数であるので、
例えば、$a=-v''(x_{A}), b=u'(x_{A})$とおけば、
$\varepsilon(x_{A},y)=ay+b$となり、これは、$y$についての1次式で
線形の(直線状の)分布になっていることがわかる。
$a=-v''(x_{A})$が傾きで、
$b=u'(x_{A})$が$x$軸の切片だから、グラフに描くなら、
図のようになる。
つまり、
梁モデル
では、軸方向ひずみ$\varepsilon$だけが存在し、
任意の断面の軸方向ひずみは、梁の桁高(けただか)$y$方向に対して線形分布
している。
これをひずみの三角形分布と呼ぶ。
 上の図のように、梁の断面上にひずみ(や次回やる応力など)の分布を
重ねて描くということはよくやられるが、
慣れないとちょっとわかりにくいかもしれないので、補足する。
図の断面$z=z_{A}$上に$y$軸を持ってきて、
$z$軸を$\varepsilon$としてグラフを描いているということである。
上の図のように、梁の断面上にひずみ(や次回やる応力など)の分布を
重ねて描くということはよくやられるが、
慣れないとちょっとわかりにくいかもしれないので、補足する。
図の断面$z=z_{A}$上に$y$軸を持ってきて、
$z$軸を$\varepsilon$としてグラフを描いているということである。
切片や傾きというと$x$が右向きで$y$が上向きの
$y=ax+b$でないとイメージしにくい人も
いるかもしれないので、念のため、
回転させた絵も貼り付けておく。
 $dz=Rd\theta$と表せるとき、
梁軸($z$)方向の直ひずみの曲げ成分
$\varepsilon_{曲げ}$を$R$と$y$を用いて表わせ。
答えはここ。
$dz=Rd\theta$と表せるとき、
梁軸($z$)方向の直ひずみの曲げ成分
$\varepsilon_{曲げ}$を$R$と$y$を用いて表わせ。
答えはここ。
 $dz=Rd\theta, \; \theta(z)=-\frac{dv(z)}{dz}$
と表せるとき、
$\varepsilon^{曲げ}$を$R$と$\theta$を用いずに表わせ。
また、$z=z_{A}$断面での$\varepsilon^{曲げ}_{zz}$の分布を図示せよ。
答えはここ。
$dz=Rd\theta, \; \theta(z)=-\frac{dv(z)}{dz}$
と表せるとき、
$\varepsilon^{曲げ}$を$R$と$\theta$を用いずに表わせ。
また、$z=z_{A}$断面での$\varepsilon^{曲げ}_{zz}$の分布を図示せよ。
答えはここ。
 梁軸($z$)方向の直ひずみののび成分が
梁軸($z$)方向の直ひずみののび成分が
$\varepsilon_{zz}^{のび}=w'(z)$
曲げ成分が
$\varepsilon_{zz}^{曲げ}=-yv''(z)$
と表されるとき、
$\varepsilon_{zz}^{のび}$の分布と
$\varepsilon_{zz}^{曲げ}$の分布をそれぞれ(別々に)図示せよ。
答えはここ。
初期状態で$z$軸に横たわる長さ$\ell$の梁の変形後のたわみが ${\displaystyle v(z)=\frac{z^{3}-3\ell z^{2}}{a^{2}}}$
軸方向変位が${\displaystyle w(z)=\frac{\Delta\ell}{\ell}z}$
で表されるとする。
このとき、梁の軸方向直ひずみ$\varepsilon_{zz}(x,y)$を求めよ。
また、
梁の中央$z=\frac{\ell}{2}$における$\varepsilon_{zz}(\frac{\ell}{2})$を求め、
$z=\frac{\ell}{2}$の断面での$\varepsilon_{zz}$の分布を図示せよ。
答え。
(マウスで領域選択すると見える):
$v'(z)=\frac{3z^{2}-6\ell z}{a^{2}}$
$v''(z)=\frac{6z-6\ell}{a^{2}}=\frac{6}{a^{2}}(z-\ell)$
$\varepsilon_{zz}^{曲げ}(x,y)=-yv''(z)=\frac{6}{a^{2}}y(\ell-z)$
$\varepsilon_{zz}^{のび}(x,y)=w'(z)=\frac{\Delta\ell}{\ell}$
よって、
$\varepsilon_{zz}(x,y)=\frac{6}{a^{2}}y(\ell-z)+\frac{\Delta\ell}{\ell}$
2022年度小テスト:
小テスト221026
2021年度小テスト:
問1,
問2,
解答
2020年度小テスト:
問1,
問2,
解答
メモ: