
構造力学IIオンライン授業用テキスト
第2回オンライン授業
以下は、構造力学IIのテキストを材料力学II用に書き換えている途中なので、 座標の表記ほか、色々とおかしいです。 小さい字は補足説明や余談なので、読み飛ばしてもいいです。
「変位」というのは、着目している点がどこに移動したかということで、 「変形」というのは、着目している物体の形が変わること。 物体の形がほとんど変形せずに、遠くまで変位することもあれば、 物体がある場所に留まってぐしゃっと大きく変形することもある。 つまり、「変位」と「変形」は違う。
 変形には「伸び縮み変形」と「せん断変形」がある。
まず、
物体の中に各辺が座標軸と平行な微小な立方体(2次元なら正方形)の要素を
考えて、その四角い要素がどのように変形するかということに
着目してみる。
簡単のため2次元で考えるとして、
例えば、図のような物体が左右に引っ張られたとして、
微小正方形要素の周辺が$x$軸方向には一様に伸び、
$y$方向には一様に縮んだとすると、
正方形要素は、頂点の直角を保ったまま長方形に変形する。
このように、物体中の微小な立方体(2次元なら正方形)要素が、
頂点の直角を保ちながら、直方体(2次元なら長方形)に変形するような変形を、
ここでは「伸び縮み変形」(または「伸縮変形」)と呼ぶ。
一方、図のような物体を微小正方形の対角線方向に斜めに引っ張ったら、
微小正方形要素は、頂点の直角がくずれて、ひし形に変形するだろう。
このように物体中の微小な立方体(2次元なら正方形)要素が、
(辺の長さは変えずに)頂点の角度を変えるような変形を
「せん断変形」(または「角度変形」)と呼ぶ。
すると、これ以外の一般的な変形
(図の微小正方形が不等辺の平行四辺形になるような)も、
「伸び縮み変形」と「せん断変形」の組合せとして表せそうだ。
変形には「伸び縮み変形」と「せん断変形」がある。
まず、
物体の中に各辺が座標軸と平行な微小な立方体(2次元なら正方形)の要素を
考えて、その四角い要素がどのように変形するかということに
着目してみる。
簡単のため2次元で考えるとして、
例えば、図のような物体が左右に引っ張られたとして、
微小正方形要素の周辺が$x$軸方向には一様に伸び、
$y$方向には一様に縮んだとすると、
正方形要素は、頂点の直角を保ったまま長方形に変形する。
このように、物体中の微小な立方体(2次元なら正方形)要素が、
頂点の直角を保ちながら、直方体(2次元なら長方形)に変形するような変形を、
ここでは「伸び縮み変形」(または「伸縮変形」)と呼ぶ。
一方、図のような物体を微小正方形の対角線方向に斜めに引っ張ったら、
微小正方形要素は、頂点の直角がくずれて、ひし形に変形するだろう。
このように物体中の微小な立方体(2次元なら正方形)要素が、
(辺の長さは変えずに)頂点の角度を変えるような変形を
「せん断変形」(または「角度変形」)と呼ぶ。
すると、これ以外の一般的な変形
(図の微小正方形が不等辺の平行四辺形になるような)も、
「伸び縮み変形」と「せん断変形」の組合せとして表せそうだ。
上の例では、微小正方形要素の各辺が座標軸と平行になるような要素を
考えることにしたが、もし微小正方形要素を45°回転させたら、
今度は、左右に引っ張るとせん断変形して、
右上と左下の斜め方向に引っ張ると伸び縮み変形するようにもできる。
つまり、伸び縮み変形とかせん断変形というのは、
どの座標系で観測するかに依存して変わってくるものであるし、
逆に言うと、どんな変形状態でも伸び縮み変形として捉えることのできる
向きがあることになる(この辺の話は「主ひずみ」
や「主応力」の話をする機会が
あれば後述)。
伸び縮み変形を数値で表すには「垂直」ひずみという物理量を使う。
 上で、
変位と変形は違うという話をした。
変位というのは、初期状態で着目した点が変形後にどこに移動したかを
表しているが、これを使って
変形を表すことはできるだろうか。
伸び縮み変形を表すには、1つの点の変位だけを調べても、
その点がどれだけ動いたかはわかっても、
その点の周囲がどれだけのびたかはわからない。
だから、2つの点の変位を調べて、2つの点の距離が最初の状態から、
のびたか縮んだかで変形の程度を表したい。
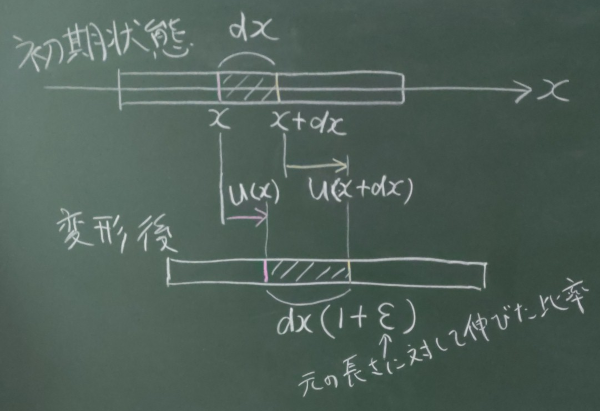
図のように初期状態で$x$軸に横たわる細長い棒があったとして、
その棒の微小部分$dx$に着目する。
初期状態でこの棒の左端が$x$にあるとすると、右端は$x+dx$にあることになる。
さて、この棒が外力を受けて変形しながら変位し、
左端が$x$方向に$u(x)$だけ、右端が$x$方向に$u(x+dx)$だけ変位したとする。
その結果、微小部分$dx$が初期状態よりちょっとだけ伸びたとする。
その初期状態よりちょっとだけ伸びた比率を、
垂直ひずみ$\varepsilon$という量で定義したい。
「垂直ひずみ」は「直ひずみ」とも言う。
つまり、伸びる方向の直ひずみを正の$\varepsilon$で表すことになるので、
縮む方向の直ひずみは、$\varepsilon<0$ということになる。
伸びることを「
上で、
変位と変形は違うという話をした。
変位というのは、初期状態で着目した点が変形後にどこに移動したかを
表しているが、これを使って
変形を表すことはできるだろうか。
伸び縮み変形を表すには、1つの点の変位だけを調べても、
その点がどれだけ動いたかはわかっても、
その点の周囲がどれだけのびたかはわからない。
だから、2つの点の変位を調べて、2つの点の距離が最初の状態から、
のびたか縮んだかで変形の程度を表したい。
図のように初期状態で$x$軸に横たわる細長い棒があったとして、
その棒の微小部分$dx$に着目する。
初期状態でこの棒の左端が$x$にあるとすると、右端は$x+dx$にあることになる。
さて、この棒が外力を受けて変形しながら変位し、
左端が$x$方向に$u(x)$だけ、右端が$x$方向に$u(x+dx)$だけ変位したとする。
その結果、微小部分$dx$が初期状態よりちょっとだけ伸びたとする。
その初期状態よりちょっとだけ伸びた比率を、
垂直ひずみ$\varepsilon$という量で定義したい。
「垂直ひずみ」は「直ひずみ」とも言う。
つまり、伸びる方向の直ひずみを正の$\varepsilon$で表すことになるので、
縮む方向の直ひずみは、$\varepsilon<0$ということになる。
伸びることを「
微小部分$dx$の右端が$u(x+dx)$だけ右に変位して、
左端が$u(x)$だけ右に変位しているから、変形後の微小部分の長さは、
以下のように表せる。
$dx(1+\varepsilon)=dx+u(x+dx)-u(x)$
これを整理すると、
${\displaystyle \varepsilon=\frac{u(x+dx)-u(x)}{dx}
}$
と書けるが、
これは$dx$がじゅうぶんに微小だという仮定のもとでの
ひずみのおおざっぱな定義である。
微小部分の長さ$dx$を極限まで小さくしてやると
これは「微分」の定義になるので、
ある点$x$の
$x$方向の垂直ひずみは次式のように$x$方向変位の$x$に関する微分として
定義できる。
$
{\displaystyle
\varepsilon(x)=\lim_{dx \to 0}\frac{u(x+dx)-u(x)}{dx}
=\frac{d u(x)}{dx}=u'(x)
}
$
なお、垂直ひずみは、伸びた比率だから無次元である。
$y$方向や$z$方向の垂直ひずみも考える場合は、それぞれ
区別する必要があるので、
$\varepsilon_{xx}$,
$\varepsilon_{yy}$,
$\varepsilon_{zz}$のように書いて添字で区別する。
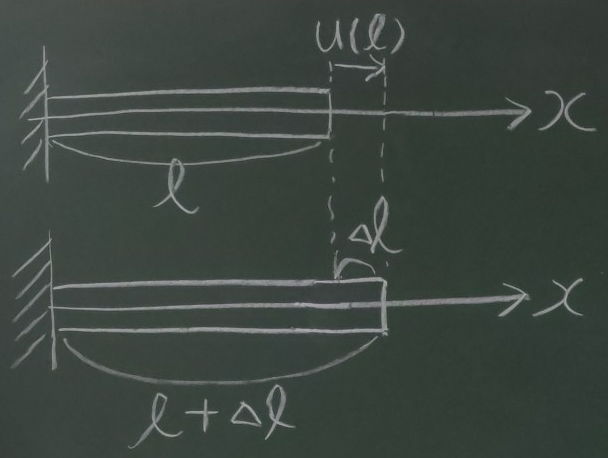 図のように初期状態で$z$軸に長さ$\ell$の棒が横たわっている。
この棒の左端が$x$軸の原点に固定されており、
右端を右方向に引っ張ったところ、
図のように棒が$\Delta\ell$だけ伸びたとする。
このとき、変形後の棒の$x$方向変位を(初期状態の$x$の関数として)
$u(x)=ax+b$のような線形の1次式で表したい。
$u(0)$と$u(\ell)$を求め、
$u(x)$を求めよ。
また、
$\varepsilon(x)$を求めよ。
図のように初期状態で$z$軸に長さ$\ell$の棒が横たわっている。
この棒の左端が$x$軸の原点に固定されており、
右端を右方向に引っ張ったところ、
図のように棒が$\Delta\ell$だけ伸びたとする。
このとき、変形後の棒の$x$方向変位を(初期状態の$x$の関数として)
$u(x)=ax+b$のような線形の1次式で表したい。
$u(0)$と$u(\ell)$を求め、
$u(x)$を求めよ。
また、
$\varepsilon(x)$を求めよ。
答え:
左端は固定されていて変位は0だから、$u(0)=b=0$
右端は初期状態から$x$の正方向に$\Delta\ell$ だけ変位しているから、
$u(\ell)=a\ell+b=a\ell=\Delta\ell$ よって、$a=\frac{\Delta\ell}{\ell}$
よって、$u(x)=\frac{\Delta\ell}{\ell}x$
$\varepsilon(x)=u'(x)=\frac{\Delta\ell}{\ell}$
重要:つまり、長さ$\ell$の棒が一様に伸びて$\ell+\Delta\ell$になった
場合の垂直ひずみは、$\varepsilon(x)=\frac{\Delta\ell}{\ell}$で表される。
注意:
$u(x)$は、初期状態での点の座標$x$の関数である。
つまり、初期状態で$x$にあった点が、変形後に、初期状態での座標から
どれだけ変位したかを表している。
変形後の点の座標の関数ではない。
(参考)
 せん断変形を数値で表すには
「せん断ひずみ」という物理量を使う。
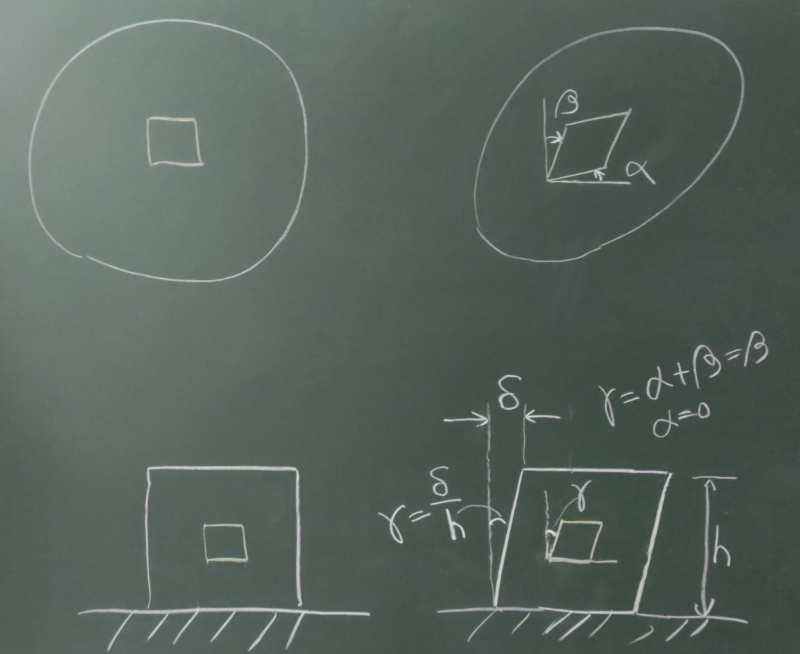
図のように初期状態で長方形だった物体内の微小部分が、
変形後に平行四辺形につぶれた(せん断変形した)とする。
このとき、ある頂点の2辺が内側にそれぞれ角度$\alpha$, $\beta$(ラジアン)だけ
回転して変形したとすると、この平面($xy$面)のテンソルせん断ひずみは、
せん断変形を数値で表すには
「せん断ひずみ」という物理量を使う。
図のように初期状態で長方形だった物体内の微小部分が、
変形後に平行四辺形につぶれた(せん断変形した)とする。
このとき、ある頂点の2辺が内側にそれぞれ角度$\alpha$, $\beta$(ラジアン)だけ
回転して変形したとすると、この平面($xy$面)のテンソルせん断ひずみは、
テンソルせん断ひずみ:
${\displaystyle
\varepsilon_{xy}=\frac{\alpha+\beta}{2}
}$
で表される。
「連続体の力学」等の理論的な分野では、$\varepsilon_{xy}$のことを
単に「せん断ひずみ」と呼ぶのが一般的であるが、
機械や土木等の分野で多様される後述の「工学せん断ひずみ」と
区別するため、ここでは「テンソルせん断ひずみ」と呼んでおく。
せん断ひずみは、角度(ラジアン)なので、無次元である。
つまり、垂直ひずみもせん断ひずみも
ひずみは無次元と理解しておけばよい。
テンソルせん断ひずみ$\varepsilon_{xy}$は、
ひずみをテンソルの成分として表したりする際に使われる
せん断ひずみで、添字の$xy$は
厳密には微分操作に対応しているが、ここでは$xy$面のせん断変形を表すせん断ひずみ
と考えておいてよい(ちなみに、テンソル成分で表した垂直ひずみは
$\varepsilon_{xx}$と表される。
一方、機械や土木、建築などの工学分野では、
以下のように$\alpha+\beta$を2で割らないものを
工学せん断ひずみとして使っている。
工学せん断ひずみ:$\gamma=\alpha+\beta$
個人的には、工学せん断ひずみのことを指す場合には、
常に「工学せん断ひずみ」または「工学的せん断ひずみ」と言った方が
望ましいとは思うが、工学せん断ひずみを単に「せん断ひずみ」と言う
ことが多いので、文献中に
せん断ひずみが現れたら、
テンソルせん断ひずみか工学せん断ひずみかを判断する
必要がある。
なお、工学せん断ひずみの物理的な解釈としては、
図のように、長方形の1辺が固定されていて、この長方形が一様に
せん断変形して平行四辺形になったような状態を考えた場合、
固定された辺に平行な方の微小長方形の1辺は回転しないので$\alpha=0$で、
鉛直な1辺の方だけが内側に$\beta$回転したとすると、
工学せん断ひずみは$\gamma=\alpha+\beta=\beta=\frac{\delta}{h}$と
表される。
補足:
材料や物理の一般の分野で「ひずみ」(英語ではstrain)と言えば、
この無次元量のことを言うのが普通だが、
日本の建築などの分野では、
無次元のひずみの意味では「ひずみ度」という言葉を用いて、
「ひずみ」の方は、長さの次元の伸びの意味で使ったりする習慣もある
(今も?)。
機械や土木やその他の分野では、こうした使い方はまずないと思うが、
「ひずみ度」という表現が出てきたときは、
「ひずみ」が次元のある量で使われている場合があるので注意が必要である。
角度$\alpha$, $\beta$を点の変位から求めるためには、
3つの頂点の変位に着目する必要がある。
梁モデルでは、
断面の図心をつらねた軸の変位($u, v, w$)しか考えないので、
こうした3点の変位とせん断ひずみを関係づけることはしないが、
2次元の物体内の点の変位とせん断ひずみとの関係について、
ちゃんと知りたい場合は、こちらを参照。
 ある程度 細長いものがちょっとだけ曲がるような問題を考える場合には、
梁モデルというのを仮定する。
図のように
割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形
(せん断ひずみ)が生じて枡目の角は直角では
なくなるだろう。
これを考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、これを考慮すべき場合は、考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、このせん断変形が無視できるような
「細長い棒が、ちょっとだけ曲がる」
場合に限定して考える。
このように、棒が曲がった後も、棒の軸線と断面とが直交し続けるような仮定を
ベルヌーイ・オイラーの仮定とか
平面保持の仮定と言い、
このような仮定を設けた棒のことを、
ベルヌーイ・オイラー梁とか初等梁と言う。
このテキストで特に注意書きなしで「梁」と書く場合は
ベルヌーイ・オイラー梁のことを指す。
ちなみに、
曲げを受ける平面内のせん断変形を考慮した梁は、
ティモシェンコ梁(Timoshenko梁)と言う。
ある程度 細長いものがちょっとだけ曲がるような問題を考える場合には、
梁モデルというのを仮定する。
図のように
割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形
(せん断ひずみ)が生じて枡目の角は直角では
なくなるだろう。
これを考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、これを考慮すべき場合は、考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、このせん断変形が無視できるような
「細長い棒が、ちょっとだけ曲がる」
場合に限定して考える。
このように、棒が曲がった後も、棒の軸線と断面とが直交し続けるような仮定を
ベルヌーイ・オイラーの仮定とか
平面保持の仮定と言い、
このような仮定を設けた棒のことを、
ベルヌーイ・オイラー梁とか初等梁と言う。
このテキストで特に注意書きなしで「梁」と書く場合は
ベルヌーイ・オイラー梁のことを指す。
ちなみに、
曲げを受ける平面内のせん断変形を考慮した梁は、
ティモシェンコ梁(Timoshenko梁)と言う。
さて、ベルヌーイ・オイラーの仮定を設けると、 せん断ひずみ成分は0になってしまい、考えなければいけないひずみは、 梁の軸方向の垂直ひずみ $\varepsilon$だけとなるので、だいぶ話が簡単になる。 それにしても、梁(の断面の各点)は軸方向にしか伸び縮みしないのに、 それで梁がたわむ(曲がる)のを表現できるのだろうか。 それについては、次回以降、考えていく。
2022年度小テスト:
小テスト221019
2021年度小テスト:
問,
解答
2020年度小テスト:
問1,
問2,
解答
メモ: