構造力学IIオンライン授業用テキスト
第13回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
さて、これまで、静定梁・不静定梁の任意点のたわみ$v(z)$を$z$の関数として 求める方法を学んできたが、 梁や構造物(トラスやラーメン)のある特定の点（例えば単純梁の中央部とか、 片持ち梁の先端とか載荷点とか）の変位だけを求めたいということは多々ある。 もちろん、任意点の変位を$z$の関数として求めておけば、 知りたい点の変位は、その点の$z$座標を代入して求めればよいわけだが、 特定の点の変位を求めればいいだけなら、 だいぶ楽に求める「便法」は各種ある。 構造物のある一点の変位を求めたい際に、 割と楽に求められる単位荷重法という方法を教えたいと思う。 単位荷重法は、補仮想仕事の原理から導かれる。 この授業では、梁のたわみを求めるのに、 エネルギーや仕事を利用した解法には、ここまで一切 触れていないが、 ここで少しだけ、仮想仕事を利用した方法も紹介しておく。
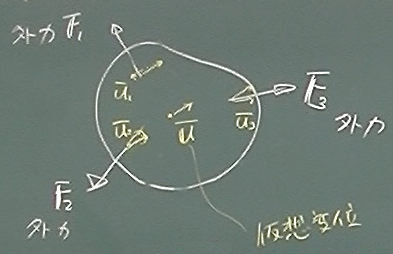まず、空中に浮かぶ剛体に対する仮想仕事の原理を説明する。
剛体というのは、変形しない物体ということだ。
今、空中に浮かぶ物体に、外力$\mathbf{F}_{1}, \mathbf{F}_{2},....\mathbf{F}_{n}$が
作用しつりあっているとする。
すると、力のつりあいから
$\sum\mathbf{F}_{i}=\mathbf{F}_{1}+\mathbf{F}_{2}+....+\mathbf{F}_{n}=0$
となる。ベクトルとして足しているが、$y, z$成分にわけて、
それぞれの成分の足し算がゼロということでもいい。
さて、この物体のすべての点が、$\overline{\mathbf{u}}$だけ仮想的に変位したとする。
剛体だから、すべての点が平行移動したことにする。
簡単のため回転移動は考えないでおく。
仮想変位は本当の変位ではなく、仮想的な「うその」変位なので、
実変位$\mathbf{u}$と区別して、
$\overline{\mathbf{u}}$のようにバーをつけておく。
今後、このバーがついているものは仮想の量ということである。
さて、上の
$\sum\mathbf{F}_{i}=0$の式に
$\overline{\mathbf{u}}$をかける（内積をとる）と、以下のようになる。
$\sum\mathbf{F}_{i}\cdot\overline{\mathbf{u}}=0$
力と変位のベクトルの内積というのは
(高校の数学か物理で$|\mathbf{a}||\mathbf{b}|\cos\theta$みたいなのをやったかと思うが、
力の向きに移動した距離をかけた）仕事を意味するわけだけど、
要は、
$\mathbf{F}_{1}, \mathbf{F}_{2},....\mathbf{F}_{n}$の外力の大きさ
$F_{1}, F_{2},....F_{n}$に、
それらの外力方向の変位成分
$\overline{u}_{1}, \overline{u}_{2},....\overline{u}_{n}$をかけて足したもの
（仮想仕事）がゼロ、
つまり
$F_{1}\overline{u}_{1}+F_{2}\overline{u}_{2}+....F_{n}\overline{u}_{n}=0$
ということである。
式を見れば、当たり前のことを言っているようだが、まあ、
当たり前のことと捉えておいていい。
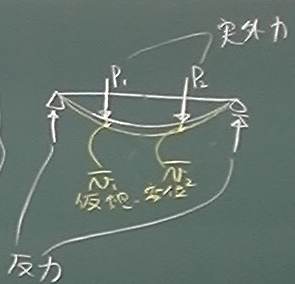一方、梁のように地面や壁に固定された弾性体の場合、
外力と反力はつりあっているものの、仮想変位を与えても、
支点は動かないので支点反力は仕事をせず、
外力のみが仕事をするから外力の仮想仕事はゼロにはならない。
つまり、外力は梁を弾性変形するのに仕事をしているのである。
だから、地面や壁に固定された弾性体に対する仮想仕事の原理は、
外力の仮想仕事が内力の仮想仕事と等しいという以下のような式になる。
$$\sum F_{i}\overline{u}_{i}=\int_{V}\sigma_{zz}\overline{\varepsilon}_{zz}dV$$
左辺が外力の仮想仕事、右辺が内力の仮想仕事である。
この式の意味は、なんとなくイメージできればいいが、
左辺は、
外力$F_{i}$にそれぞれの外力方向の仮想変位
$\overline{u}_{i}$をかけた
$F_{i}\overline{u}_{i}$を合計したものである。
右辺の内力の仮想仕事は、
構造物内部のあらゆる点の応力$\sigma_{zz}$に、
仮想変位$\overline{u}_{i}$によって生じたその点の
仮想ひずみ$\overline{\varepsilon}_{zz}$をかけたものを
体積積分$\int_{V}dV$で合計しているということ。
一般的な物体の内部では、
第4回でやった直応力・せん断応力や
第2回でやった直ひずみ・せん断ひずみの
成分が一通り発生しているが、ここでは、梁（せいぜいトラス）しか扱わないので、
梁モデルの仮定が成り立つものとして、
軸方向の直応力$\sigma_{zz}$と軸方向の
仮想直ひずみ$\overline{\varepsilon}_{zz}$だけを考えることにする。
仮想仕事の原理は、 本当の外力が仮想的な変位を通じてする仕事であるが、 これの逆で、 仮想的な外力が本当の変位を通じてする仕事に対しても同様に、 以下のような関係が成り立ち、これを補仮想仕事の原理と言う。 以上は、イメージをつかんでもらうためのかなり大雑把な説明だが、 より詳しい正確な解説に興味がある人は、 図書館で構造力学公式集などを参照してほしい。 $$\sum \overline{F}_{i}u_{i} =\int_{V}\overline{\sigma}_{zz}\varepsilon_{zz}dV$$
さて、上の補仮想仕事の原理を天下り的に受け入れるとして、
実変位を知りたい点に実変位方向の仮想外力として単位荷重$\overline{1}$を
与えると、
左辺はこの単位荷重$\overline{1}$と単位荷重方向への実変位$\delta$との積となる。
$$\overline{1}\cdot\delta=\int_{V}\overline{\sigma}_{zz}\varepsilon_{zz}dV$$
第5回でやったように、
軸方向の直応力を のび成分と曲げ成分に分解すると、
$\sigma_{zz}(y,z)=\sigma_{zz}^{のび}(y,z)+\sigma_{zz}^{曲げ}(y,z)$
$\sigma_{zz}^{のび}(y,z)=\frac{N(z)}{A}$
$\sigma_{zz}^{曲げ}(y,z)=\frac{M(z)}{I}y$
仮想外力$\overline{F}$によって生じる仮想応力にもこれらの関係を
適用すると以下のようになる。
$\overline{\sigma}_{zz}(y,z)=\overline{\sigma}_{zz}^{のび}(y,z)+\overline{\sigma}_{zz}^{曲げ}(y,z)$
$\overline{\sigma}_{zz}^{のび}(y,z)=\frac{\overline{N}(z)}{A}$
$\overline{\sigma}_{zz}^{曲げ}(y,z)= \frac{\overline{M}(z)}{I}y$
これらを上の補仮想仕事の原理の右辺に代入しながら、
式を変形していく。
まず、体積積分$\int_{V}dV$は、
梁の断面についての面積積分$\int_{A}dA$をしてから、
それをさらに梁の長さ$\ell$について$\int_{0}^{\ell}dz$で
積分すればよい。
$$\int_{0}^{\ell}\int_{A}
(\overline{\sigma}_{zz}^{のび}\varepsilon_{zz}^{のび}
+
\overline{\sigma}_{zz}^{曲げ}\varepsilon_{zz}^{曲げ})
dAdz$$
$$=\int_{0}^{\ell}\int_{A}
(\frac{\overline{N}}{A}\varepsilon_{zz}^{のび}+
\frac{\overline{M}}{I}y\varepsilon_{zz}^{曲げ})dAdz$$
$$=\int_{0}^{\ell}\int_{A}
(\frac{\overline{N}}{EA}E\varepsilon_{zz}^{のび}+
\frac{\overline{M}}{EI}yE\varepsilon_{zz}^{曲げ})dAdz$$
$$=\int_{0}^{\ell}\int_{A}
(\frac{\overline{N}}{EA}\sigma_{zz}^{のび}+
\frac{\overline{M}}{EI}y\sigma_{zz}^{曲げ})dAdz$$
$$=\int_{0}^{\ell}\int_{A}
(\frac{\overline{N}}{EA}\frac{N}{A}+
\frac{\overline{M}}{EI}\frac{M}{I}y^{2})dAdz$$
ここで、面積積分$\int_{A}dA$を実行するが、面積積分は$xy$断面に
対する積分なので、$N(z)$や$M(z)$といった$z$だけの関数は積分する必要はなく、
第1項めは、$A=\int_{A}dA$をかければよい。
第2項目は、$y^{2}$がかかっているので、これは積分する必要があり、
実行すると
第5回でやった断面2次モーメント
$I=\int_{A}y^{2}dA$になる。
$$=\int_{0}^{\ell}
(\frac{\overline{N}}{EA}\frac{N}{A}A+
\frac{\overline{M}}{EI}\frac{M}{I}I)dz$$
$$=\int_{0}^{\ell}
(\frac{\overline{N}N}{EA}+
\frac{\overline{M}M}{EI})dz$$
最終的に、以下の公式が得られる。
${\displaystyle \overline{1}\cdot\delta
=\int_{0}^{\ell}
(\frac{\overline{N}N}{EA}+
\frac{\overline{M}M}{EI})dz\;\;\;\;\;
}$
(重要)
左辺は、実変位$\delta$に仮想の単位荷重$\overline{1}$をかけたものだから、
$\delta$そのものとなるが、式の物理的意味としては
外力の補仮想仕事を表すことを強調して、
$\overline{1}\cdot\delta$と書いておく。
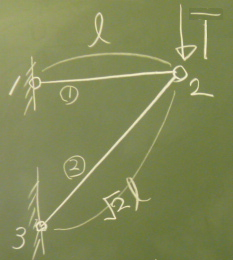
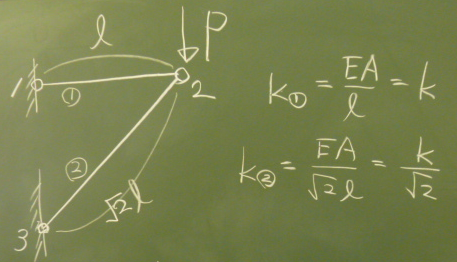図のような2部材のトラスの
載荷点(節点2)の$y$方向変位と$z$方向変位を求めてみたい。
トラスは最低3部材ないとトラスと言わないのではないかとか、
反力が4個で求まらないのではないかとか、その辺の細かいことは
置いておく。
まずは部材力を求めておこう。
反力は4個だが、
ためしに内的静定・不静定を
判定してみると、部材数$m=2$, 反力数$r=4$, 節点数$j=3$で、
$m+r-2j=2+4-2\times 3=0$で内的静定だ。
というわけで、たぶん部材力は求まりそうだ。
トラス部材①も②も、同じ材料、同じ断面で伸び剛性は$EA$
とする。そうすると、
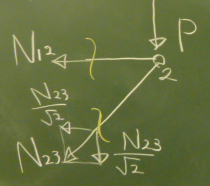図のように2部材をそれぞれ切断し、（反力を使わなくていい）右側の
ピースを取り出す。
$\Sigma\downarrow=P+\frac{N_{23}}{\sqrt{2}}=0$
$\Sigma\rightarrow=-N_{12}-\frac{N_{23}}{\sqrt{2}}=0$
$N_{23}=-\sqrt{2}P$
$N_{12}=P$
単位荷重法で、
まずは節点2の下($y$)方向の変位を求める。
そのためには、元の構造の（元の外力は外してから）
変位を求めたい点の
求めたい変位の方向に仮想単位荷重$\overline{1}$を与えて、
この仮想単位荷重によって生じる仮想部材力を求める。
今、変位を求めたい点は節点2で、
求めたい変位の方向は$y$方向なので、
節点2の$y$方向に仮想単位荷重$\overline{1}$を与えることになる。
仮想の（うその）荷重だということを強調するために、$\overline{1}$と
バーをつけているが、単なる単位荷重$1$である。
すると、上の問題の$P$が$\overline{1}$に変わっただけだから、
上で求めた部材力の$P$に$1$を代入すれば、仮想単位荷重によって生じる
仮想部材力が求まる。
仮想部材力には上バーをつけて表すことにすると、
$\overline{N}_{23}=-\sqrt{2}$
$\overline{N}_{12}=1$
そうすると、節点2の下方向変位$v_{2}$は、
公式から、
$$\overline{1}\cdot v_{2}
=\int_{全部材}\frac{N\overline{N}}{EA}dz_{局所}$$
を計算すればよい。曲げモーメントは作用していないので、軸力の項だけを
計算すればよい。
公式では、梁の全長を$\ell$とした積分の式に
なっているが、部材が複数ある場合は、
それぞれの部材について、その部材軸に沿って部材長だけ積分することになる。
その場合の$z$座標は、部材軸に沿った局所座標になるので、
添字「局所」をつけて
局所座標系を表している。
すべての部材について、$N$と$\overline{N}$をかけて、
それぞれの軸に沿って端から端まで
（要は、部材が横たわっている局所系の$z_{局所}$に沿って）
その部材の長さぶんの積分をすればいいのだけど、
トラスの部材力というのは、
それぞれの部材について、端から端まで同じ値で定数だから、
端から端まで積分するというのは、単にその部材の長さ
（例えば$\ell=\int_{0}^{\ell}dz_{局所}$）をかければいいことになる。
つまり、
$$\overline{1}\cdot v_{2}
=\int_{全部材}\frac{N\overline{N}}{EA}dz_{局所}$$
$$=\frac{1}{EA}
\left(N_{12}\overline{N}_{12}\ell +N_{23}\overline{N}_{23}\cdot\sqrt{2}\ell
\right)$$
$$=\frac{1}{EA}
\left(P\cdot 1\cdot\ell +(-\sqrt{2}P)(-\sqrt{2})\cdot \sqrt{2}\ell
\right)$$
$$=(1+2\sqrt{2})\frac{P\ell}{EA}$$
つまり、
${\displaystyle v_{2}=(1+2\sqrt{2})\frac{P\ell}{EA}}$
と求まる。
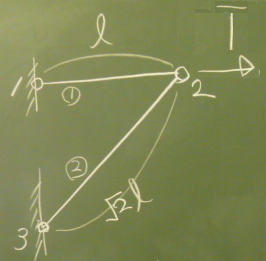次に、節点2の右($z$)方向変位$w_{2}$も
求める。
そのためには、元の構造の（元の外力は外してから）
変位を求めたい点の
求めたい変位の方向に仮想単位荷重$\overline{1}$を与えて、
この仮想単位荷重によって生じる仮想部材力を求める。
つまり、節点2に求めたい右方向の仮想単位荷重
$\overline{1}$を与えて、この仮想単位荷重によって生じる
仮想部材力を求める。
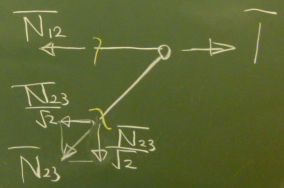さきほどと同様に部材を2箇所で切って、
（反力を考えなくていい）右側のピースを取り出す。
$\Sigma\rightarrow=-\overline{N}_{12}+1=0$
$\Sigma\downarrow=\frac{\overline{N}_{23}}{\sqrt{2}}=0$
$\overline{N}_{12}=1$
$\overline{N}_{23}=0$
あとは、公式に従ってもとの構造（下向きの$P$が節点2に作用している）の部材力$N$と
今回の仮想構造（右向きの$1$が節点2に作用している）
の部材力$\overline{N}$をかけて積分すればよい。
$$\overline{1}\cdot w_{2}
=\int_{全部材}\frac{N\overline{N}}{EA}dz^{\ell}$$
$$=\frac{1}{EA}
\left(N_{12}\overline{N}_{12}\ell +N_{23}\overline{N}_{23}\cdot\sqrt{2}\ell
\right)$$
$$=\frac{1}{EA}\left(P\cdot 1\cdot\ell + (-\sqrt{2}P)\cdot 0 \cdot\sqrt{2}\ell
\right)$$
$$=\frac{P\ell}{EA}$$
つまり、
${\displaystyle w_{2}=\frac{P\ell}{EA}}$
と求まる。
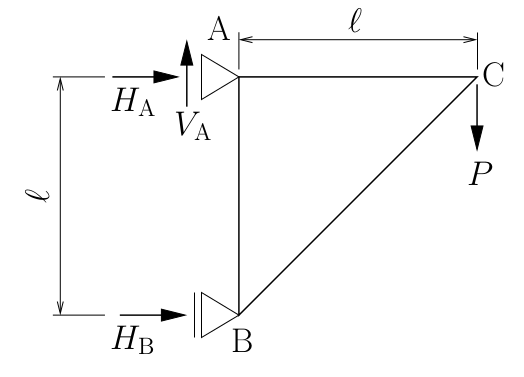節点Cの鉛直下方向変位、水平右方向変位を求めよ。
ただし、すべての部材の伸び剛性は$EA$とする。
右の図は、
2017年度の構造力学IIの定期試験の問題。
答えは、
ここ。
上の2部材トラスと似ているが、部材ABにも部材力が発生するので、
答えは変わってくる。
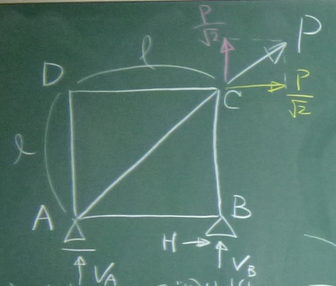点Cの荷重方向（つまり右上$45^{\circ}$方向）の変位を求めよ。
すべての部材の伸び剛性は$EA$とする。
答えは
ここ。
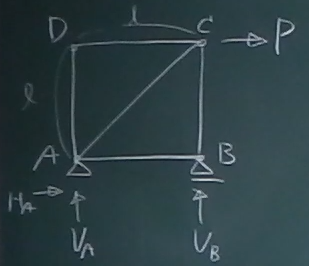点Cの鉛直変位、水平変位を求めよ。
すべての部材の伸び剛性は$EA$とする。
答えの動画解説はここ
2022年度小テスト：
小テスト230125
2021年度小テスト：
問,
解答
2020年度小テスト：
問1-2,
解答
メモ:
