マトリクス構造解析オンライン授業用テキスト
第7回オンライン授業
オンライン用テキストの準備中：6/24(水)までに用意します。 小さい字は補足説明なので、読み飛ばしてもいいです。
さて、前回、
軸力のない梁の剛性方程式を紹介したが、
これだと、軸力のある問題は解けないし、
座標変換もできない。
だから、（軸力が作用してなくても）まっすぐの棒しか解けない。
骨組だのラーメンだのが解けるようにするには、座標変換できるように
しなければいけない。
$
\left(
\begin{array}{c}
S_{1}\\
M_{1}\\
S_{2}\\
M_{2}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
\theta_{1}\\
v_{2}\\
\theta_{2}
\end{array}
\right)
$
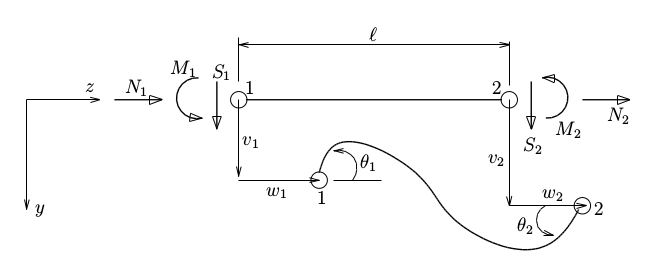
鉛直方向の
節点力$S_{1}, S_{2}$や節点変位$v_{1}, v_{2}$に関しては、
第3回の ばね要素でやったように、
水平方向の節点力$N_{1}, N_{2}$や節点変位$w_{1}, w_{2}$と組み合わせて、
$(S_{1}, N_{1})$,
$(S_{2}, N_{2})$,
$(v_{1}, w_{1})$,
$(v_{2}, w_{2})$
といった2次元のベクトルにしてしまえば、
座標変換できるようになる。
第3回の ばね要素のときは、
せん断力成分$S_{1}$や$S_{2}$は生じていないのに、
座標変換できるようにするために、強引に導入した。
だから、剛性マトリクスのせん断成分がぜんぶ0みたいな変なマトリクスを
使った。
今回は、水平方向（軸方向）の剛性には、ちゃんと、ばねの剛性方程式を
適用すれば、それらを組み合わせるだけで、
いいのではないだろうか。
あれ、ばね要素のときと同様に、
$(S_{1}, N_{1})$,
$(S_{2}, N_{2})$,
$(v_{1}, w_{1})$,
$(v_{2}, w_{2})$
がベクトルとして座標変換できるのはいいとして、
モーメント$M_{1}, M_{2}$や回転角$\theta_{1}, \theta_{2}$は、
どうすればいいのだろうか。
実は、2次元の場合、$yz$平面上のモーメントというのは、
常に$x$軸右ねじまわりのモーメントで、
$yz$平面上の回転角というのは、常に$x$軸右ねじまわりの回転角なので、
全体座標系($yz$系)でも、
局所座標系($y^{\ell}z^{\ell}$)系でも、大きさが変わらない。
つまり、2次元の場合は、座標が回転しても、
座標変換する必要がないのである。
というわけで、上記の軸力のない梁の剛性方程式と、
ばねの剛性方程式を
組み合わせてみる。
ここで注意が必要である。
第3回の ばね要素のときにも
話したが、右手系の座標変換行列で座標変換するには、
ベクトルの成分の並べ順を$x\rightarrow y\rightarrow z$の順に
並べなければならない。
ここでは $yz$座標系を使っているから、$y\rightarrow z$の順だ。
そうすると、節点力は、
$(S_{1}, N_{1})$のようにせん断力成分、軸力成分の順になるし、
節点変位は、$(v_{1}, w_{1})$のように、軸直角変位成分、軸方向変位成分の
順になる。
モーメントや回転角は、ある意味、どこに入れてもよいが、
節点力、節点変位の次に入れることにして、
節点1, 節点2の順に節点力ベクトル、節点変位ベクトルを並べると、
以下のように、軸力がある梁の剛性方程式が与えられる。
全体系の梁の剛性方程式（軸力あり）
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
M_{1}\\
S_{2}\\
N_{2}\\
M_{2}
\end{array}
\right)
=
\left(
\begin{array}{cccccc}
\frac{12EI}{\ell^{3}} & 0 &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}& 0 &
-\frac{6EI}{\ell^{2}} \\
0 & \frac{EA}{\ell} & 0 & 0 & -\frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} \\
0 & -\frac{EA}{\ell} & 0 & 0 & \frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
w_{1}\\
\theta_{1}\\
v_{2}\\
w_{2}\\
\theta_{2}
\end{array}
\right)
$
曲げ剛性を$EI$で書いているのに合わせて、
ばね定数も
伸び剛性$EA$の方で$k=\frac{EA}{\ell}$を使って
書いておく。
この梁の剛性方程式は、$yz$座標の$z$軸に梁が横たわる梁の剛性方程式なので、
違う座標系を使っているテキストや論文の剛性方程式の
並び方や成分の符号は、これとは違う形になる。
文献にのっている剛性方程式（梁要素に限らず、板要素でも立体要素でも）を
利用してプログラムを組んだりする場合は、
常に、どういう座標系を用いて、節点力や節点変位がどう定義されているか
ということに注意を払う必要がある。
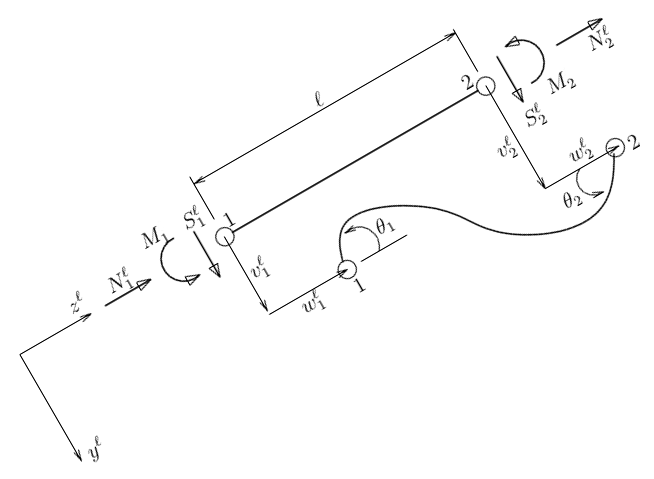さて、骨組やラーメンなど、様々な向きを向いた要素を扱うには、
第3回のばね要素のときと同様に、
要素の軸の向きが$z^{\ell}$となるような
局所系($y^{\ell}z^{\ell}$系)で、
局所系の剛性方程式をつくり
（局所系で見ている人にとっては、上の全体系の剛性方程式と同じ形になる）、
それを座標変換して、全体系の節点力、節点変位で表してから、
重ね合わせて全体剛性方程式を組み立てればよい。
というわけで、
全体系($yz$系)より$x$軸右ねじまわりに$\phi$だけ回転した
局所系($y^{\ell}z^{\ell}$系)で、
剛性方程式を考えると、
節点力や節点変位の記号が違うだけで、
($y^{\ell}z^{\ell}$系)における$y^{\ell}$方向、$z^{\ell}$方向の力学挙動は、
($yz$系)における$y$方向、$z$方向の力学挙動と同じだから、
局所系の剛性方程式が、上の全体系の剛性方程式の
節点力と節点変位を局所系の記号で置き換えたものとして、以下のように得られる。
今回、節点変位ベクトルの回転角成分に$\theta$の記号を使っているので、
座標変換のための座標の回転量は、紛らわしいので$\phi$を用いることにする。
局所系の梁の剛性方程式（軸力あり）
$
\left(
\begin{array}{c}
S_{1}^{\ell}\\
N_{1}^{\ell}\\
M_{1}\\
S_{2}^{\ell}\\
N_{2}^{\ell}\\
M_{2}
\end{array}
\right)
=
\left(
\begin{array}{cccccc}
\frac{12EI}{\ell^{3}} & 0 &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}& 0 &
-\frac{6EI}{\ell^{2}} \\
0 & \frac{EA}{\ell} & 0 & 0 & -\frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} \\
0 & -\frac{EA}{\ell} & 0 & 0 & \frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}^{\ell}\\
w_{1}^{\ell}\\
\theta_{1}\\
v_{2}^{\ell}\\
w_{2}^{\ell}\\
\theta_{2}
\end{array}
\right)
\ \\
$
これを全体系に座標変換するには、
第4回の ばね要素のときのように、
剛性マトリクスの両側から、座標変換の転置行列と座標変換行列とをかけて
やれば、よさそうだ。
ちょっと違うのは、モーメントと回転角があることだ。
さっき言ったように、2次元平面では、モーメントや回転角は座標変換
する必要がない。
どうしたらいいだろう。
モーメントと回転角を考えなければ、
第4回の ばね要素と同様に、
全体系の節点力、節点変位は、座標変換行列$\mathbf{T}$を用いて、
以下の関係が成り立つだろう。
$
\left(
\begin{array}{c}
S_{1}^{\ell}\\
N_{1}^{\ell}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
S_{1}\\
N_{1}
\end{array}
\right)
\\
$
$
\left(
\begin{array}{c}
S_{2}^{\ell}\\
N_{2}^{\ell}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
S_{2}\\
N_{2}
\end{array}
\right)
\\
$
$
\left(
\begin{array}{c}
v_{1}^{\ell}\\
w_{1}^{\ell}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
v_{1}\\
w_{1}
\end{array}
\right)
\\
$
$
\left(
\begin{array}{c}
v_{2}^{\ell}\\
w_{2}^{\ell}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
v_{2}\\
w_{2}
\end{array}
\right)
\ \\
$
では、上の節点力ベクトルと節点変位ベクトルの末尾に、
モーメントの成分と回転角の成分を加えて、
それらには、何もしない座標変換行列を定義しなおしたらどうだろうか。
つまり、全体系から局所系への座標変換行列を、
以下のように定義しなおすと、
$
\mathbf{T}
=
\left(
\begin{array}{rrr}
\cos\phi & \sin\phi & 0 \\
-\sin\phi & \cos\phi & 0 \\
0 & 0 & 1
\end{array}
\right)
\ \\
$
各節点の全体系における節点力と節点変位は、
$\mathbf{T}$を用いて以下のように
局所系に座標変換できる。
$
\left(
\begin{array}{c}
S_{1}^{\ell}\\
N_{1}^{\ell}\\
M_{1}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
M_{1}
\end{array}
\right)
\\
$
$
\left(
\begin{array}{c}
S_{2}^{\ell}\\
N_{2}^{\ell}\\
M_{2}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
S_{2}\\
N_{2}\\
M_{2}
\end{array}
\right)
\\
$
$
\left(
\begin{array}{c}
v_{1}^{\ell}\\
w_{1}^{\ell}\\
\theta_{1}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
v_{1}\\
w_{1}\\
\theta_{1}
\end{array}
\right)
\\
$
$
\left(
\begin{array}{c}
v_{2}^{\ell}\\
w_{2}^{\ell}\\
\theta_{2}
\end{array}
\right)
=\mathbf{T}
\left(
\begin{array}{c}
v_{2}\\
w_{2}\\
\theta_{2}
\end{array}
\right)
\ \\
$
つまり、モーメントと回転角に対しては、何も変えないといことだ。
さて、これらを上の
局所系の梁の剛性方程式に代入して整理すれば、
第4回の ばね要素の全体系の剛性方程式
と同様に、
以下のような形の全体系の梁の剛性方程式が得られる。
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
M_{1}\\
S_{2}\\
N_{2}\\
M_{2}
\end{array}
\right)
=
\left(
\begin{array}{ll}
\mathbf{T}^{T} & \mathbf{O}\\
\mathbf{O} & \mathbf{T}^{T}\\
\end{array}
\right)
\left(
\begin{array}{cccccc}
\frac{12EI}{\ell^{3}} & 0 &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}& 0 &
-\frac{6EI}{\ell^{2}} \\
0 & \frac{EA}{\ell} & 0 & 0 & -\frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} \\
0 & -\frac{EA}{\ell} & 0 & 0 & \frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{cc}
\mathbf{T} & \mathbf{O}\\
\mathbf{O} & \mathbf{T}\\
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
w_{1}\\
\theta_{1}\\
v_{2}\\
w_{2}\\
\theta_{2}
\end{array}
\right)
\ \\
$
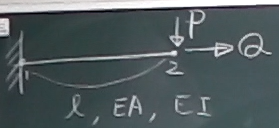図のような片持ち梁の先端に、鉛直荷重と水平荷重が
作用している問題を1要素の梁の要素剛性方程式で解いてみる。
外力条件は、$S_{2}=P, N_{2}=Q$, それ以外は0.
境界条件は、$v_{1}=w_{1}=\theta_{1}=0$
よって、
$
\left(
\begin{array}{c}
0\\
0\\
0\\
P\\
Q\\
0
\end{array}
\right)
=
\left(
\begin{array}{cccccc}
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 &
\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} \\
0 & 0 & 0 & 0 & \frac{EA}{\ell} & 0 \\
0 & 0 & 0 &
\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
w_{1}\\
\theta_{1}\\
v_{2}\\
w_{2}\\
\theta_{2}
\end{array}
\right)
\ \\
$
5行目は、$Q=\frac{EA}{\ell}w_{2}$だから、$w_{2}=\frac{Q\ell}{EA}$.
これはフックの法則のばねの伸びを求めてるだけ。
4行目と6行目は、
$\frac{P\ell^{3}}{12EI}=v_{2}+\frac{\ell}{2}\theta_{2}$
$0=v_{2}+\frac{2\ell}{3}\theta_{2}$
これらを連立させて、
$\theta_{2}=-\frac{P\ell^{2}}{2EI}$,
$v_{2}=\frac{P\ell^{3}}{3EI}$.
これは前回、
軸力のない片持ち梁で計算したのと同じ答え。
求まった節点変位を、もとの要素剛性方程式に代入して、
節点の近傍で切り離された切断面に作用する内力としての
節点力を求める。
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
M_{1}\\
S_{2}\\
N_{2}\\
M_{2}
\end{array}
\right)
=
\left(
\begin{array}{cccccc}
\frac{12EI}{\ell^{3}} & 0 &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}& 0 &
-\frac{6EI}{\ell^{2}} \\
0 & \frac{EA}{\ell} & 0 & 0 & -\frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} & 0 &
\frac{6EI}{\ell^{2}} \\
0 & -\frac{EA}{\ell} & 0 & 0 & \frac{EA}{\ell} & 0 \\
-\frac{6EI}{\ell^{2}} & 0 &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} & 0 &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
0\\
0\\
0\\
\frac{P\ell^{3}}{3EI}\\
\frac{Q\ell}{EA}\\
-\frac{P\ell^{2}}{2EI}
\end{array}
\right)
=
\left(
\begin{array}{c}
-4P+3P\\
-Q\\
2P\ell-P\ell\\
4P-3P\\
Q\\
2P\ell-2P\ell\\
\end{array}
\right)
=
\left(
\begin{array}{c}
-P\\
-Q\\
-P\ell\\
P\\
Q\\
0\\
\end{array}
\right)
\ \\
$
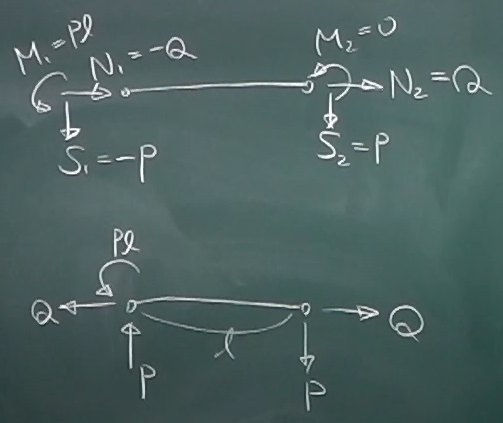求まった内力としての節点力
($S_{1}$とか$N_{1}$とか)を、そのまま描いてみる。
次に、実際の向きで描き直してみる。
軸方向は$Q$の引張が作用してつりあっている。
鉛直方向は上に$P$と下に$P$でつりあっているが、
時計回りに$P\ell$のモーメントが発生する。
そのモーメントと左端の反時計まわりに$P\ell$のモーメントが
つりあっている。
