マトリクス構造解析オンライン授業用テキスト
第3回オンライン授業
オンライン用テキストの準備中：5/27(水)までに用意します。 小さい字は補足説明なので、読み飛ばしてもいいです。
今までは、$z$軸上の1次元の世界に浮かぶ ばね要素を扱ってきたが、
トラスのように斜めになった部材を扱うためには、
($z$軸に対して)斜めになった ばね要素も扱える必要がある。
トラスでは、力の方向や変位の方向は、鉛直、水平の2方向だから、
$z$軸だけの1次元の座標では、
トラスは扱えない。
そこで、下向き$y$, 右向き$z$とする2次元の$yz$座標系を考える。
下向きを$y$方向とするのは、下にたわむ梁とかを扱う構造力学の
慣習にならってである。
ばね要素が$z$軸に横たわっていれば、
前回まででやった ばねの剛性方程式がそのまま成り立つ。
でも、トラスとかでは、
いろんな向きに部材が横たわっているから、
$z$方向に節点力$N_{1}, N_{2}$や
節点変位$w_{1}, w_{2}$が定義された$z$軸上で成り立つ
剛性方程式は、$z$軸から斜めに傾いた軸方向に横たわるばね要素については、
適用できない。
だったら、
ばねが傾いていても、その傾いた軸を$z$軸としてやれば、
前回までの剛性方程式がそのまま使えるのではないだろうか。
でも、水平のもともとの$z$軸とは、違う向きの軸なので、
同じ記号を使うわけにはいかない。
そこで、$yz$座標系を
$x$軸右ねじ回りに$\theta$だけ回転した
局所座標系として
$y^{\ell}z^{\ell}$座標系を考える。
添字の$^{\ell}$は、局所系の($\ell oca\ell$)という意味である。
$z^{\ell}$軸上に横たわる ばね要素に対して、
図のように$z^{\ell}$方向に
節点力
$N_{1}^{\ell}, N_{2}^{\ell}$,
節点変位
$w_{1}^{\ell}, w_{2}^{\ell}$を定義してやれば、
それら$z^{\ell}$方向の節点力、節点変位に対しては、
$z$軸上で成り立つばねの剛性方程式が、
そのまま成り立つので、以下のように書けるだろう。
$
\left(
\begin{array}{c}
N_{1}^{\ell}\\
N_{2}^{\ell}
\end{array}
\right)
=
\left(
\begin{array}{cc}
k & -k \\
-k & k
\end{array}
\right)
\left(
\begin{array}{c}
w_{1}^{\ell}\\
w_{2}^{\ell}
\end{array}
\right)
$
そうすると、局所座標系で表された節点力や節点変位と、
もともとの$yz$座標系（これを全体座標系と言う）で表された
節点力や節点変位との間の関係を求めることができれば、
どんな向きで表された剛性方程式も全体座標系の
節点力と節点変位で表せるのではないだろうか。
そうすれば、第2回でやった$z$軸上でつながった2要素のように、
色んな方向を向いている ばね要素の剛性方程式を、
全体座標系で表して重ね合わせることができるのではないだろうか。
節点力ベクトル
$(N_{1}^{\ell}, N_{2}^{\ell})$や
節点変位ベクトル
$(w_{1}^{\ell}, w_{2}^{\ell})$はベクトルだけど、
ある座標で表されたベクトルを
違う座標で表すにはどうすればいいだろうか。
そうだ。
座標変換というツールがあった。
座標変換してやれば、局所系で表されたベクトルを
全体系で表したり、全体系で表されたベクトルを局所系で
表したりできるのではないだろうか。
でも、まだ、なんかおかしい気がする。
$(N_{1}^{\ell}, N_{2}^{\ell})$や
$(w_{1}^{\ell}, w_{2}^{\ell})$はベクトルといっても、
$N_{1}^{\ell}$も$N_{2}^{\ell}$も
$w_{1}^{\ell}$も$w_{2}^{\ell}$もすべて
$z^{\ell}$方向に定義された量だ。
$(w_{1}^{\ell}, w_{2}^{\ell})$の2つの成分は、
節点1と節点2の$z^{\ell}$方向変位という意味であって、
$y^{\ell}z^{\ell}$座標系で表された変位ベクトルの
$y^{\ell}$方向成分、$z^{\ell}$方向成分という意味ではない。
力や変位を2次元ベクトルとして座標変換するためには、
$y^{\ell}$と$z^{\ell}$の2方向の成分がないと座標変換はできない。
それなら、$y^{\ell}$方向の節点力と$y^{\ell}$方向の節点変位も定義してしまえば
いいのではないだろうか。
ということで、図のように、$y^{\ell}$方向を正とする節点力$S_{1}^{\ell}, S_{2}^{\ell}$と、
$y^{\ell}$方向を正とする節点変位$v_{1}^{\ell}, v_{2}^{\ell}$をそれぞれ節点1, 節点2について
定義する。
といっても、この要素はあくまで ばね要素で、
両端ヒンジのトラス要素と考えた方がわかりやすいかもしれないが、
要は、どんな外力が加えられても、
ばね要素には軸力しか作用しない。
つまり、$z^{\ell}$軸に横たわる ばね要素の場合、
実際には、$S_{1}^{\ell}$と$S_{2}^{\ell}$のせん断力成分はゼロで、
$N_{1}^{\ell}$と$N_{2}^{\ell}$だけが値を持つということになる。
ただ、$y^{\ell}z^{\ell}$座標系で見ると、
$N_{1}^{\ell}$の成分しかないとしても、
これを全体系の$yz$座標系で見ると、
$S_{1}$と$N_{1}$とに分解されて、
$S_{1}$成分も持つということになるので、
座標変換できるためには、形式的に$y^{\ell}z^{\ell}$の2成分のベクトルと
$yz$の2成分のベクトルどうしで変換し合う必要がある。
そうすると、この ばね要素の剛性方程式はどのように書けるだろうか。
節点力ベクトルは、節点1, 節点2の順で、
更に右手系の$y^{\ell}\rightarrow z^{\ell}$の順に並べると、
$(S_{1}^{\ell}, N_{1}^{\ell}, S_{2}^{\ell}, N_{2}^{\ell})$となり、
同様に節点変位は、
$(v_{1}^{\ell}, w_{1}^{\ell}, v_{2}^{\ell}, w_{2}^{\ell})$となる。
テキストによっては、$xy$座標系で、
ばね要素が$x$軸に横たわっているものもある。
その場合、軸力は$x$方向になるので、
右手系の順に$x\rightarrow y$と並べると、軸力成分、せん断力成分の
順になる。
では、局所座標系($y^{\ell}z^{\ell}$系)の$z^{\ell}$軸に横たわる ばね要素に対する
要素剛性方程式を書いてみるが、
この ばね要素には せん断力成分$S_{1}^{\ell}, S_{2}^{\ell}$は
生じないので、$S_{1}^{\ell}, S_{2}^{\ell}$の行の剛性マトリクスの成分は
全て0にならないといけない。軸力成分の$N_{1}^{\ell}, N_{2}^{\ell}$は、
ばねの伸び成分とばね定数で結び付けられているので、
厳密には
すべての節点変位が関係するが、
ここで扱う現象は、トラスの各部材がそれぞれの部材軸方向に伸び縮みして、
それ以外の方向の変位は非常に小さいような場合を考える。
つまり、ここで考える座標変換というのは、
トラスの各部材が初期状態で全体座標系から斜め方向に横たわっていることを
考慮するためのもので、
外力による変位・変形によって、部材が傾いたことを考慮するためのものではない。
それも厳密に考慮したいということになると
幾何学非線形解析ということになる
(トラスだと回転量が節点変位に含まれないので、それも厄介な話だが)。
というようなわけで、細かいことを考えなければ、
任意の局所座標系
$y^{\ell}z^{\ell}$座標系の$z^{\ell}$軸に
横たわる ばね要素に成り立つ要素剛性方程式は、
局所系で定義される節点力や節点変位を用いれば、
以上の考察から、形式的に以下のように書ける。
$
\left(
\begin{array}{c}
S_{1}^{\ell}\\
N_{1}^{\ell}\\
S_{2}^{\ell}\\
N_{2}^{\ell}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
0 & 0 & 0 & 0 \\
0 & k & 0 & -k \\
0 & 0 & 0 & 0 \\
0 & -k & 0 & k \\
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}^{\ell}\\
w_{1}^{\ell}\\
v_{2}^{\ell}\\
w_{2}^{\ell}
\end{array}
\right)
$
これは、両端が節点1, 節点2の要素についての要素剛性方程式だが、
同様に、
両端が節点2, 節点3の要素だの、
両端が節点3, 節点1の要素だの、
様々な方向を向いた局所座標系で、同様に居所系の要素剛性方程式が、
このように書ける。
それを座標変換で全体系で表すことができれば、
節点力と節点変位を重ね合わせできるのではないだろうか。
重ね合わせは次回に回すが、
まずは、座標変換のやり方を考えてみる。
局所座標系($y^{\ell}z^{\ell}$系)の$z^{\ell}$軸に横たわる ばね要素の
節点1の節点変位$v_{1}^{\ell}, w_{1}^{\ell}$を
全体座標系($yz$系)の節点変位$v_{1}, w_{1}$を使って表す方法を考える。
まず、図のように、$y^{\ell}, z^{\ell}$の正方向に、
節点1が
$v_{1}^{\ell}, w_{1}^{\ell}$だけ変位しているとする。
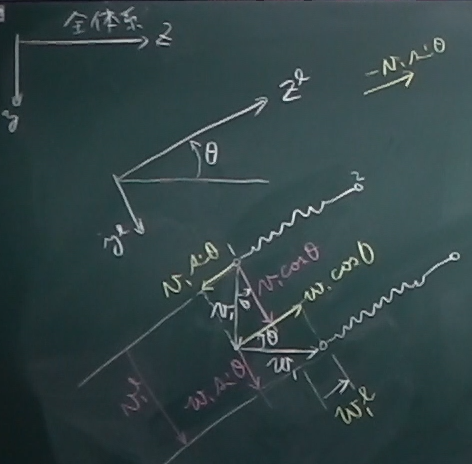この状態を$y, z$方向の変位$v_{1}, w_{1}$で表してやり
(見えにくいけど、図の白い矢印で書いた$v_{1}, w_{1}$)、
それらの$y^{\ell}, z^{\ell}$方向成分を求めてやれば、
$v_{1}^{\ell}, w_{1}^{\ell}$を$v_{1}, w_{1}$で表せる。
$y^{\ell}z^{\ell}$系は、$yz$系より$x$軸右ねじ回りに$\theta$だけ回転している
から、三角関数を使って、
$v_{1}, w_{1}$をそれぞれ
$y^{\ell}, z^{\ell}$方向成分に分解してやる。
そうすると、$v_{1}$の
$y^{\ell}$方向成分は$v_{1}\cos\theta$,
$z^{\ell}$方向成分は$-v_{1}\sin\theta$となる。
この$z^{\ell}$方向成分は
左向き($z^{\ell}$の負方向)
に$v_{1}sin\theta$だけど、$z^{\ell}$の正方向には、$-v_{1}sin\theta$となる。
また、$w_{1}$の
$y^{\ell}$方向成分は$w_{1}\sin\theta$,
$z^{\ell}$方向成分は$w_{1}\cos\theta$となる。
そうすると、$y^{\ell}, z^{\ell}$方向の成分をそれぞれ足してやると、
以下のように
$v_{1}^{\ell}, w_{1}^{\ell}$を
$v_{1}, w_{1}$で表すことができる。
$v_{1}^{\ell}=v_{1}\cos\theta+w_{1}\sin\theta$
$w_{1}^{\ell}=-v_{1}\sin\theta+w_{1}\cos\theta$
これをマトリクスを使って表せば以下のようになる。
$
\left(
\begin{array}{c}
v_{1}^{\ell}\\
w_{1}^{\ell}
\end{array}
\right)
=
\left(
\begin{array}{cc}
\cos\theta & \sin\theta \\
-\sin\theta & \cos\theta
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
w_{1}
\end{array}
\right)
$
このマトリクスを太文字の
$\mathbf{T}$を使って
$
\mathbf{T}=
\left(
\begin{array}{cc}
\cos\theta & \sin\theta \\
-\sin\theta & \cos\theta
\end{array}
\right)
$
と書くことにするが、この$\mathbf{T}$は、
全体系のベクトルにかけて局所系のベクトルに変換する行列なので、
全体系から局所系への座標変換行列
とか、
全体系から局所系への座標変換マトリクスと言う。
ということは、局所系のベクトルにかけて全体系に変換する
局所系から全体系への座標変換行列もあるということだが、
それはどうすれば導けるだろうか。
もちろん、上の例と同様に、
今度は、
$v_{1}^{\ell}, w_{1}^{\ell}$の
$yz$方向成分を図形的に導いてもいいが、
せっかく$\mathbf{T}$があるのだから、
これを使って逆関係を求めればよい。
さて、どうやって逆関係を求めるか。
まあ、少し考えれば、逆行列を求めればいいんだが、
線形代数で教わった方法(最近の世代だと$2\times 2$の
逆行列を高校ではやらなかったりするが、少なくとも理工系の
大学では$4\times 4$以上の一般的な逆行列の求め方もやるだろう)で、
公式を使えばちゃちゃっと求まると思うが、
実は2次元の座標変換行列の逆行列は転置行列で表される。
2025/4/22まで、「転置行列で表される」を
間違って「対称行列で表される」と書いてました。
すいません。動画の方は「転置」と言ってますね。
つまり、
$
\mathbf{T}^{-1}=
\mathbf{T}^{T}=
\left(
\begin{array}{cc}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{array}
\right)
$
となる。
これを使えば、
以下のように局所系のベクトルにかけて全体系のベクトルに変換することができる。
$
\left(
\begin{array}{c}
v_{1}\\
w_{1}
\end{array}
\right)
=
\mathbf{T}^{T}
\left(
\begin{array}{c}
v_{1}^{\ell}\\
w_{1}^{\ell}
\end{array}
\right)
$
この
$\mathbf{T}^{T}$を
局所系から全体系への座標変換行列
と言う。
テキストや論文によっては、
局所系から全体系への座標変換行列の方を$\mathbf{T}$と
定義していることもある。
その場合、$\mathbf{T}$と$\mathbf{T}^{T}$が逆になるので
注意が必要である。
次回やるが、この$\mathbf{T}$と$\mathbf{T}^{T}$があれば、
局所系の節点力や節点変位を全体系に変換したり、
その逆ができる。
節点力についても、
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}
\end{array}
\right)
=
\mathbf{T}^{T}
\left(
\begin{array}{c}
S_{1}^{\ell}\\
N_{1}^{\ell}
\end{array}
\right)
$
とか
$
\left(
\begin{array}{c}
S_{2}^{\ell}\\
N_{2}^{\ell}
\end{array}
\right)
=
\mathbf{T}
\left(
\begin{array}{c}
S_{2}\\
N_{2}
\end{array}
\right)
$
とか、各節点の$yz$成分、$y^{\ell}z^{\ell}$成分どうしで変換できる。
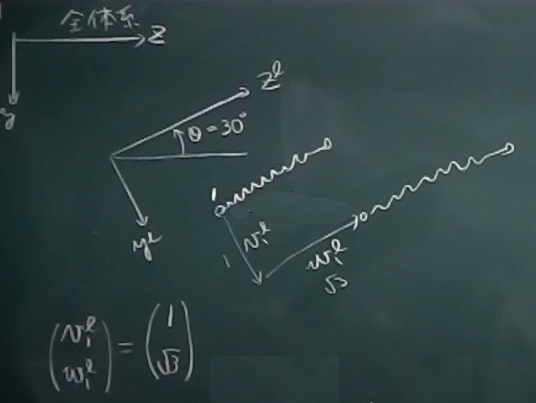今回は簡単な例題。
図のように全体系($yz$系)から$x$軸右ねじ回りに$30^{\circ}$回転した
局所系($y^{\ell}z^{\ell}$系)において、
節点1の節点変位が局所系で、
$(v_{1}^{\ell}, w_{1}^{\ell})=(1, \sqrt{3})$と与えられるとき、
全体系で表した節点変位$(v_{1}, w_{1})$はどのように与えられるか。
2022年度 小テスト第3回
問題1,
問題2,
解答
2021年度 小テスト第3回：
問題,
解答
2020年度 小テスト第3回：
問題,
解答
